節理巖質邊坡樁基加固的穩定性分析

敬靜，饒秋華，劉利松

(1. 中南大學 資源與安全工程學院，湖南 長沙，410083；2. 中南大學 土木工程學院，湖南 長沙，410075；3. 中航規劃建設長沙設計研究院有限公司，湖南 長沙，410014)

在巖土工程中，巖質邊坡通常會發生沿節理滑動的邊坡失穩破壞，已成為巖土工程界廣泛關注的熱點問題之一。目前，國內外主要采用數值方法來研究節理巖質邊坡穩定性問題，如采用有限元與強度折減法相結合的方法研究了均質土坡[1]和節理巖質邊坡[2-3]的穩定性及其邊坡破壞機制[4-5]，采用有限差分法和強度折減法計算了層狀巖質邊坡的破壞模式，并分析了巖體幾何參數和強度參數對邊坡穩定性的滑動面[6-7]。為了提高節理巖質邊坡的穩定性，工程中多采用打樁、設置錨索等加固措施，通過數值方法研究結構面在加樁情況下的剪切特性[8]、抗滑樁對含軟弱夾層邊坡的加固效應[9-11]等。但是，關于承載樁對節理巖質邊坡穩定性影響研究甚少。含有樁基加固的節理巖質邊坡受力特性復雜，樁既要承受來自上部建筑的荷載，又要抵抗滑坡推力，起到承重與阻滑的雙重功效。在此，本文作者采用有限差分法軟件FLAC3D分別建立無樁和樁加固的節理巖質邊坡的三維計算模型并開展其穩定性分析，研究不同節理面傾角、樁長、樁位置對節理巖質邊坡穩定性的影響規律以及樁身受力與變形特性，為節理巖質邊坡的樁基加固設計與穩定性提高提供理論依據。

1 節理巖質邊坡穩定性計算

1.1 計算模型

選取如圖1 所示的節理巖質邊坡ABCDEF，總高為30 m、坡高為15 m、寬度為55 m。內含單一的貫穿節理GH，節理面出露點H 距離坡腳點E 高度為3.75 m、水平距離為1.25 m，傾角為α，且節理面無軟弱夾層。取巖石、節理的基本參數如表1 和2 所示。

采用FLAC3D軟件建模，建立圖1 所示的邊坡平面模型，巖體選取六面體單元、節理為接觸面單元，且巖體與節理的本構模型均為摩爾庫侖模型。施加邊界條件為：邊坡底部為固定邊界、左右兩側固定X 方向位移、前后兩側為固定Y 方向位移。

圖1 節理巖質邊坡數值計算模型(單位：m)Fig.1 Numerical calculated model of jointed rock slope

設節理面的下出露點H 保持不變，選取不同的節理面傾角α 分別為20°，25°，30°和35°，計算在豎向均布壓力p=100 kPa 作用下該節理巖質邊坡的安全系數。

表1 巖石計算參數Table 1 Calculation parameters of rock

表2 節理計算參數Table 2 Calculation parameters of joint

1.2 穩定性分析

圖2 節理面傾角對節理巖質邊坡(無樁)安全系數的影響Fig.2 Effect of joint inclination angle on factor of safety of jointed rock slope (without pile)

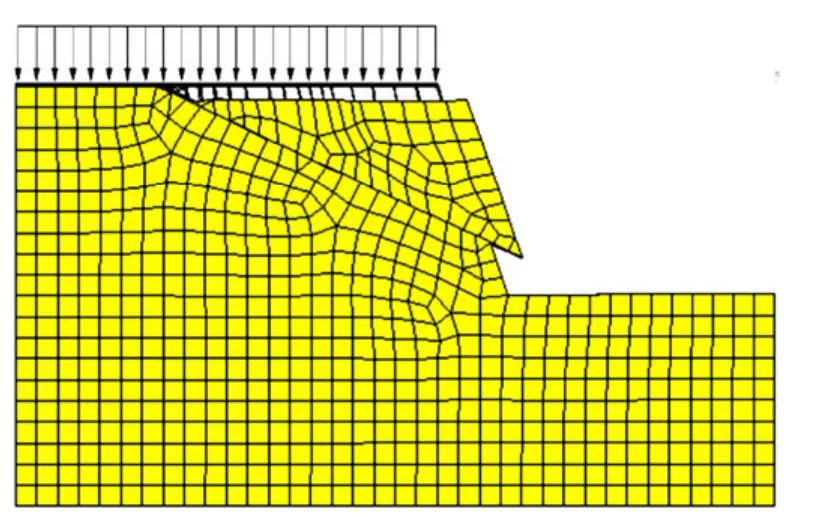
圖3 節理巖質邊坡(無樁)破壞形式(α=25°)Fig.3 Failure form (without pile) of jointed rock slope(α=25°)

2 節理巖質邊坡的樁加固分析

2.1 計算模型

樁加固節理巖質邊坡數值計算模型如圖4 所示。在節理巖質邊坡(圖1)中進行樁加固，設加固樁IJ 的直徑為1.5 m、總長度為L1、節理上部樁長為L2、節理面上出露點G 距邊坡頂端F 距離為α1、樁頂部I 距邊坡頂端F 距離為a2。加固樁采用樁單元建模，設樁的密度dp=2 500 kg/m3、彈性模量Ep=2.8×1010Pa。因樁底端嵌固在巖體中，其z 方向位移較小可忽略不計，故設z 方向位移為0 m。

為了研究節理巖質邊坡的樁加固效應，計算在豎向均布壓力p=100 kPa 的作用下，具有不同樁長(L1=8 m，10 m，12 m，14 m，16 m，18 m，20 m)、樁位置(a2=1 m，3 m，5 m，7 m)的節理巖質邊坡的安全系數，并分析其樁身受力與變形特性。

圖4 樁加固節理巖質邊坡數值計算模型(單位：m)Fig.4 Numerical model of jointed rock slope reinforced by pile foundation

2.2 樁長對節理巖質邊坡穩定性的影響

2.2.1 樁總長L1

圖5 所示為計算得到的不用節理面傾角α(固定H點)下的邊坡安全系數n 隨樁總長L1的變化曲線。可見，對于具有相同節理傾角α 的樁加固巖質邊坡，其安全系數n 隨著L1增大而增加直至某一臨界樁長L0后趨于穩定。這是因為樁對節理巖質邊坡的加固主要是在節理面上部區域，當L1＜L0時，樁身越長其加固效果越好；當L1＞L0時，樁身逐漸向邊坡底部發展，繼續增加樁長對節理面上部區域的加固效果不明顯，即對邊坡穩定性影響不大，這與均質巖坡的計算結果一致[12]。

圖5 樁總長對節理巖質邊坡安全系數的影響(a2=5 m)Fig.5 Effect of total pile length on factor of safety of jointed rock slope (a2=5 m)

對于具有相同樁長的加固巖質邊坡，隨著節理傾角α 增加，n 減小，這是因為α 越大，滑坡體越陡，致使邊坡更加容易下滑，則安全系數越小。

2.2.2 節理上部樁長L2

法院認定，公司在與成銳協商調整工作崗位時大幅調低成銳的月工資標準的行為顯失公平，其以雙方未就上述工作崗位調整方案達成一致為由解除雙方勞動關系不符合法律規定，公司應向成銳支付違法解除勞動合同賠償金。對成銳的相關訴訟請求，法院予以支持。

為了研究處于節理不同部位的樁長對節理巖質邊坡中樁基加固效果的影響，固定總樁長L1和節理上部樁長L2(取L1=18 m，L2=7.5 m)，同時改變節理面傾角α 和樁位置a2，計算節理巖質邊坡的安全系數如表3所示。可見：當L1和 L2保持不變時，同時改變節理面傾角α 和樁位置a2對節理巖質邊坡安全系數影響不大。但是僅保持樁長L1不變，單一改變節理面傾角α或者樁位置a2，L2會隨之改變，則節理巖質邊坡的安全系數會發生較大變化。因此節理上部樁長L2是影響樁加固巖質邊坡效果的決定性長度參數。

對于相同的樁總長L1和樁位置a2，隨著節理面傾角α 的不斷增加，節理上部樁長L2逐漸減小，樁對節理巖質邊坡的加固效果隨之降低，則節理巖質邊坡的安全系數逐漸變小。

表3 節理巖質邊坡安全系數(L1=18 m，L2=7.5 m)Table 3 Factor of safety of jointed rock slope(L1=18 m, L2=7.5 m)

2.2.3 節理相對樁長L2/L1

為了研究處于節理不同部位的相對樁長對節理巖質邊坡中樁基加固效果的影響，固定節理面傾角α 和相對樁長L2/L1(取α=25°，L2/L1=0.5)，同時改變樁長L1和L2(即改變樁位置a2)，計算得到的節理巖質邊坡安全系數如表4 所示。可見：當同時改變L1和L2但L2/L1保持不變時，節理巖質邊坡的安全系數n 會發生較大變化。可見，L2/L1對安全系數不起決定作用。

表4 節理巖質邊坡安全系數(α=25°,L2/L1=0.5)Table 4 Factor of safety of jointed rock slope(α=25°, L2/L1=0.5)

2.3 樁位置對節理巖質邊坡穩定性的影響

圖6 所示為相同樁總長L1下，改變傾角α 和樁位置a2得到的節理巖質邊坡安全系數。可見：對于同一節理傾角α，隨著a2的不斷增大，節理上部樁長L2逐漸減小，安全系數逐漸減低。當a2較小時(如a2在0～3 m 內)，樁位置靠近坡面附近，處在節理下滑體的主體區(圖3)，加固作用類似，則安全系數n 變化緩慢。當a2較大即樁位置遠離坡面時，L2較小，加固效果迅速降低，則安全系數n 急劇減少。

對于相同樁總長L1、樁位置a2的節理巖質邊坡，節理面傾角α 越大，滑動面越陡越容易下滑，故安全系數越小。對于固定巖質邊坡，打樁位置應靠近坡面(a2較小)，盡量增加節理上部樁長L2，以提供更大的節理有效支擋長度和邊坡抗滑力，提高樁加固效果。

圖6 樁位置對邊坡安全系數的影響(L1=18 m)Fig.6 Effect of pile location on factor of safety (L1=18 m)

2.4 加固樁的內力與位移分析

以樁長L1=18 m，樁位置a2=5 m 為例，計算不同節理面傾角α下節理巖質邊坡的樁身彎矩、剪力及樁頂位移。

2.4.1 樁身剪力分布

圖7 所示為計算得到的不同節理面傾角α 下節理巖質邊坡的樁身剪力分布圖。其中z=0 表示樁頂部。可見：樁身剪力均呈周期性波形分布，2 個樁身彎矩分布最大正剪力基本相等，且遠小于最大負剪力。隨著α 增大，剪力逐漸增大，當α=35°時，增幅最大。這是因為，當α 增加時，下滑體更易下滑，樁身承擔的剪力隨之增加。

圖7 樁身剪力分布Fig.7 Shear stress distribution of pile

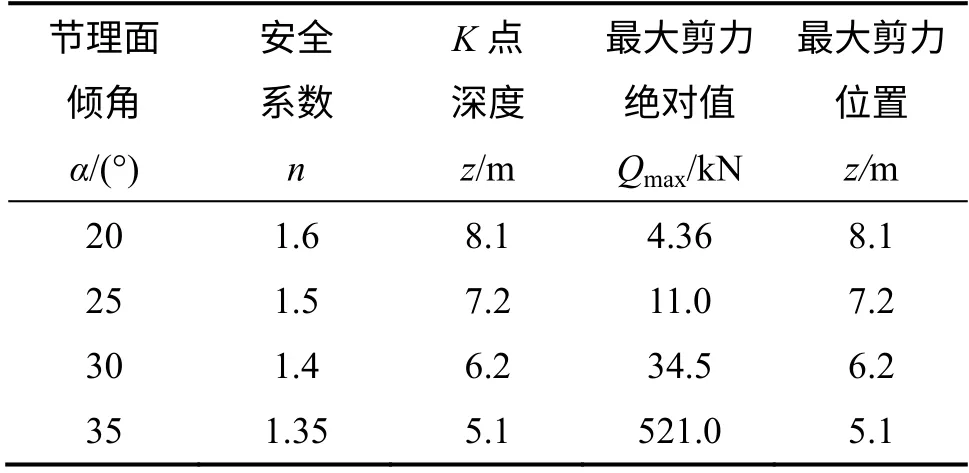
表5 樁與節理面相交點處的深度及樁身最大剪力計算結果(L1=18 m, a2=5 m)Table 5 Intersection point depth of pile and joint and calculated results of maximum shear force (L1=18 m, a2=5 m)

表5 列出了樁與節理面相交點K 處(圖4)的深度(IK 長度即為L2)、樁身最大剪力絕對值和位置。比較可得，樁身最大剪力絕對值位置與K 點重合(即出現在節理面上)，因為樁與節理面的相交點K 相當于一個鉸支點，在鉸支處樁身剪力達到最大值。

2.4.2 樁身彎矩分布

圖8 所示為計算得到的不同節理面傾角α下節理巖質邊坡的樁身彎矩分布圖。可見：樁身彎矩均呈周期性波形分布，最大彎矩隨節理面傾角α的增加而增大，且α=35°時增幅最大。與樁身剪力類似，為防止具有較大節理面傾角(更易下滑)的節理巖質邊坡失穩，樁所承受的最大彎矩越大。

圖8 樁身彎矩分布(有節理)Fig.8 Bending moment distribution of pile (with joint)

表6 列出了樁身最大正、負彎矩和位置以及對應的剪力。可見：樁身最大正負彎矩出現在剪力約等于0 kN 的截面。

為了比較無節理和含節理的樁加固巖質邊坡中的彎矩分布，圖9 所示為無節理巖質邊坡中樁身彎矩分布圖(其中z=0 表示坡頂面)[13-14]。可見：無節理樁加固巖質邊坡樁身彎矩分布呈非對稱分布，彎矩隨著深度的增加而增加，在較小范圍內達到最大值，之后樁身彎矩隨著樁身急劇減小，達到零點后，出現極小的反方向彎矩，最后又衰減至0 kN·m。顯然，含節理巖質邊坡的樁身彎矩分布規律與均質巖坡不同。這是因為節理巖質邊坡中的樁基受力更為復雜，節理面的存在導致節理面處應力分布不連續，當滑坡體沿著節理面下滑時，基樁同時承受側向坡體的水平推力和節理面下部巖體的抗力，抗力與推力相互平衡造成了正負彎矩相近的基樁彎矩分布形式。

表6 樁身最大彎矩計算結果Table 6 Calculation results of maximum bending moment of pile

圖9 樁身彎矩分布(無節理)Fig.9 Bending moment distribution of pile (without joint)

2.4.3 樁頂水平位移

圖10 所示為相同樁長下，具有不同節理面傾角α和樁位置a2下節理巖質邊坡的樁頂水平位移Δx。樁頂水平位移主要由2 部分組成：一部分是整個巖土體在坡頂均布壓力作用下由于整體側移而產生的樁頂水平位移Δx1，另一部分是上部巖體在坡頂均布壓力作用下沿節理面滑動而產生的樁頂水平位移Δx2[15]。當節理面傾角α 較小時(α=20°～30°)，下滑體不易沿節理面滑動，樁頂水平位移Δx 主要為巖體受外力作用產生的整體側移Δx1，且Δx1與樁位置a2無關，故Δx 不隨a2的變化而變化。當節理面傾角α 較大時(α=35°)，下滑體更易沿節理面滑出，由此產生的Δx2起主導作用，且Δx2與樁位置a2有關，故Δx 隨著a2的增加而增加且遠大于Δx1。可見：當節理面傾角小于巖石的摩擦角時，樁頂水平位移不受樁位置a2的影響；但當節理面傾角大于巖石的摩擦角時，樁頂水平位移隨著樁位置a2的增加(逐漸遠離坡面)而急劇增大。

因此，當節理巖質邊坡的節理面傾角較大時，為控制樁頂水平位移，布樁位置應靠近邊坡坡面(使L2較大)，提高節理巖質邊坡的安全系數越大。

圖10 樁頂水平位移隨樁位置的變化情況(L1=18 m)Fig.10 Change of horizontal displacement of pile top with pile location variation (L1=18 m)

3 結論

(1) 樁總長L1存在某一臨界樁長L0，當L1＜L0時，樁身越長其加固效果越好；當L1＞L0時，增加樁長對邊坡穩定性的提高影響不大。節理上部樁長L2是影響樁加固巖質邊坡效果的決定性長度參數，L2越大加固效果越好。

(2) 樁位置a2對節理巖質邊坡穩定性影響表現為：當a2較小即樁位置靠近坡面時，樁的加固效果變化不大；當a2較大即樁位置遠離坡面時，L2較小，加固效果急劇降低。

(3) 樁身剪力呈周期性波形分布，2 個最大正剪力基本相等，遠小于最大負剪力，且樁身最大剪力絕對值出現樁與節理面的相交點處。樁身彎矩也呈周期性波形分布，最大彎矩出現處剪力約等于0 kN。樁身剪力和彎矩均隨著節理面傾角的增大而增大。

(4) 當節理面傾角小于巖石的摩擦角時，樁頂水平位移不受樁位置a2的影響；但當節理面傾角大于巖石的摩擦角時，樁頂水平位移隨著樁位置a2的增加(逐漸遠離坡面)而急劇增大。

(5) 在實際工程中，對于一定的節理巖質邊坡樁基加固，樁總長L1應小于臨界樁長L0，盡可能布置樁在坡面附近(a2較小，L2較大)，以減少樁頂水平位移，提高節理巖質邊坡的安全系數。

[1] Griffiths D V, Lane P A. Slope stability analysis by finite elements[J]. Geotechnique, 1999, 49(3)： 387-403.

[2] Dawson E M, Roth W H, Drescher A. Slope stability analysis by strength reduction[J]. Geotechnique, 1999, 49(6)： 835-840.

[3] 鄭穎人, 趙尚毅. 有限元強度折減法在土坡與巖坡中的應用[J]. 巖石力學與工程學報, 2004, 23(19)： 3381-3388.ZHENG Yingren, ZHAO Shangyi. Application of strength reduction fem in soil and rock slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(19)： 3381-3388.

[4] 林杭, 曹平, 李江騰, 等. 層狀巖質邊坡破壞模式及穩定性的數值分析[J]. 巖土力學, 2010, 31(10)： 3300-3304.LIN Hang, CAO Ping, LI Jiangteng, et al. Numerical analysis of failure modes and stability of stratified rock slopes[J]. Rock and Soil Mechanics, 2010, 31(10)： 3300-3304.

[5] 鄭穎人, 趙尚毅, 鄧衛東. 巖質邊坡破壞機制有限元數值模擬分析[J]. 巖石力學與工程學報, 2003, 22(12)： 1943-1952.ZHENG Yingren, ZHAO Shangyi, DENG Weidong. Numerical simulation on failure mechanism of rock slope by strength reduction fem[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(12)： 1943-1952.

[6] 張德佳. 含軟弱夾層巖質邊坡穩定性分析及加固效應研究[D].重慶： 重慶交通大學土木建筑學院, 2010： 12-20.ZHANG Dejia. The research of stability analysis and reinforcement measures of slope with weak interlayer[D].Chongqing： Chongqing Jiaotong University. School of Civil Engineering and Architecture, 2010： 12-20.

[7] 宋維勝, 李江騰. 幾何參數和強度參數對邊坡三維穩定性的影響[J]. 中南大學學報(自然科學版), 2013, 44(4)： 1634-163.SONG Weisheng, LI Jiangteng. Effect of geometry parameters and strength parameters to three-dimensional stability of slope[J].Journal of Central South University (Science and Technology),2013, 44(4)： 1634-163.

[8] 劉自由, 江學良, 林杭. 軟弱結構面加樁剪切特性的數值分析[J]. 中南大學學報(自然科學版), 2011, 42(5)： 1461-1466.LIU Ziyou, JIANG Xueliang, LIN Hang. Numerical analysis for shear characteristic of soft structure plane with pile reinforcement[J]. Journal of Central South University (Science and Technology), 2011, 42(5)： 1461-1466.

[9] 陳樂求, 楊恒山, 林杭. 抗滑樁加固邊坡穩定性及影響因素的有限元分析[J]. 中南大學學報(自然科學版), 2011, 42(2)：490-494.CHEN Leqiu, YANG Hengshan, LIN Hang. Finite element analysis for slope stability and its influencing factors with pile reinforcement[J]. Journal of Central South University (Science and Technology), 2011, 42(2)： 490-494.

[10] 徐愛民, 柳群義, 朱自強, 等. 層狀巖體邊坡抗滑樁加固效應的數值分析[J]. 中南大學學報 (自然科學版), 2011, 42(8)：2453-2458.XU Aimin, LIU Qunyi, ZHU Ziqiang, et al. Numerical analysis for reinforcement response of pile in stratified rock slope [J].Journal of Central South University (Science and Technology),2011, 42(8)： 2453-2458.

[11] 韓斌, 鄭祿璟, 王少勇, 等. 復雜破碎露天邊坡的綜合加固技術[J]. 中南大學學報 (自然科學版), 2013, 44(2)： 772-777.HAN Bin, ZHENG Lujing, WANG Shaoyong, et al. Synthetic reinforcement of complicated and broken open pit slope[J].Journal of Central South University (Science and Technology),2013, 44(2)： 772-777.

[12] 王緒勇. 高層建筑下的節理巖體邊坡穩定性研究[D]. 青島：山東科技大學土木工程與建筑學院, 2011： 6-22.WANG Xuyong. Stability evaluation research on jointed rock slopes under high buildings[D]. Qingdao： Shandong University of Science and Technology. School of Civil Engineering and Architecture, 2011： 6-22.

[13] 趙明華, 劉建華, 楊明輝. 傾斜荷載下高陡邊坡橋梁基樁內力計算[J]. 巖石力學與工程學報, 2006, 25(11)： 2352-2357.ZHAO Minghua, LIU Jianhua, YANG Minghui. Inner-force calculation of bridge pile foundation in high-steep rock slope under inclined loads[J]. Chinese Journal of Geotechnical Engineering, 2006, 25(11)： 2352-2357.

[14] 劉建華, 趙明華, 楊明輝. 高陡巖質邊坡上橋梁基樁模型試驗研究[J]. 巖土工程學報, 2009, 31(3)： 372-377.LIU Jianhua, ZHAO Minghua, YANG Minghui. Model tests on bridge pile foundation in high and steep rock slopes[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(3)： 372-377.

[15] Chong W L, Haque A, Ranjith P G, et al. Effect of joints on p-y behaviour of laterally loaded piles socketed into mudstone[J].International Journal of Rock Mechanics & Mining Sciences,2011, 48(3)： 372-379.