風電場短期風速預測的MRA-SVM模型

楊亞蘭，徐耀良，鐘紹山，謝江媛

（上海電力學院電力與自動化工程學院，上海 200090）

開發和利用風能的主要形式是風力發電[1]，隨著風電容量占電力系統比重的日益增加，風電的出力預測對電網的影響不容忽視，而出力的預測主要取決于風速的預測。在時間尺度上，風速預測主要分為超短期、短期、中長期。超短期預測一般是30min以內的預測[2]，用于對發電機的控制；中長期預測時間主要集中在未來幾天至幾個月，用于風電場的規劃設計；短期預測是30min～72 h的預測，用于電力系統的功率平衡和調度、交易及暫態穩定評估等，其準確性直接影響電力系統在未來一段時間內的調度計劃。

有關風速短期預測的問題，國內外學者進行了大量的研究，歐盟國家、美國等風電產業發展較早，大都開發出了專門的風電功率預報系統，預測時長可達到72 h，相應的預測成本也比較高[3]。我國的風力發電還處于初級階段，預測的時間長度一般集中在30min～3 h時間段，預測誤差范圍[1～3]為25%～40%，預測方法的選擇很大程度上影響著預測結果的精確性。

風速預測方法主要有物理模型法和時間序列模型法。物理模型法基于大量的氣象、地表等因素和發電機的性能，其準確度主要依賴于氣象模型，準確性的保證就必須在更長時間內不斷校正，數據量大且不易獲取，計算成本高，不適用于風速的短期預測；時間序列法基于統計學習理論，包括傳統的持續預測法、卡爾曼濾波法、隨機時間序列法、空間相關性法以及人工神經網絡法，這些方法易于建模，并能夠及時地預測[4～5]。但是，傳統的時間序列法缺乏非線性處理能力，人工神經網絡方法過多地強調克服學習錯誤而泛化能力不強，容易陷入局部最小化，使得預測推廣能力較差[6～7]；支持向量機SVM（support vector machine）作為繼人工神經網絡之后的又一種統計學習方法，對于處理具有小樣本、非線性、高維數特點的序列有很好的適應性[8]。該算法利用最小化原則，引入了間隔概念，使得所建立的模型只由少數支持向量決定，減小了模型對于全部數據的依耐性[9]。

此外，影響風速變化的氣象因素十分復雜，使得風電場風速呈非平穩變化的特點，風速v與風能E呈三次方關系[10]，當風速頻繁波動時，對風機的保養是極其不利的。然而，從頻率特性來看，風速具有特殊的周期性，通過多分辨率分析MRA（multiresolution analysis），可將其看成是不同頻率的分量的疊加，每個分量處于平穩變化狀態，近似地呈周期變化，從而具有更強的預測性[10～11]。

對華東地區某風場的實際運行情況進行調研，發現預測風速的平均絕對誤差高達40%，并且以人工估算為主。當風電容量不斷增大時，這個誤差會對電網產生不良影響。因此，選擇有效的算法模型，提高風速預測的準確率，為調度部門提供可靠的數據基礎具有現實的指導意義。本文通過對該風場實測風速數據建立多分辨率分析和支持向量機（MRA－SVM）模型，預測風電場未來4 h的風速值，實現了風速的多步預測，并與SVM方法進行比較，通過均方根誤差RMSE（root mean square error）和平均相對誤差MAPE（mean absolute percentage error）來評價模型的性能，取得了較好的預測效果。

1 MRA-SVM模型原理

為降低原始風速序列的非平穩性，增強其可預測性，對風速進行n層小波分解，所得細節系數為d1，d2，…，dn，近似系數為a1，a2，…，an，則x=a3+d1+d2+d3。對分解的各系數d1，d2，…，dn及an進行單支重構，得D1，D2，…，Dn及An。通過選擇合理的核函數和懲罰因子等參數，對重構的風速序列分別進行SVM回歸預測，并將單支預測風速進行疊加，即為原始風速序列的預測數據。模型流程如圖1所示。

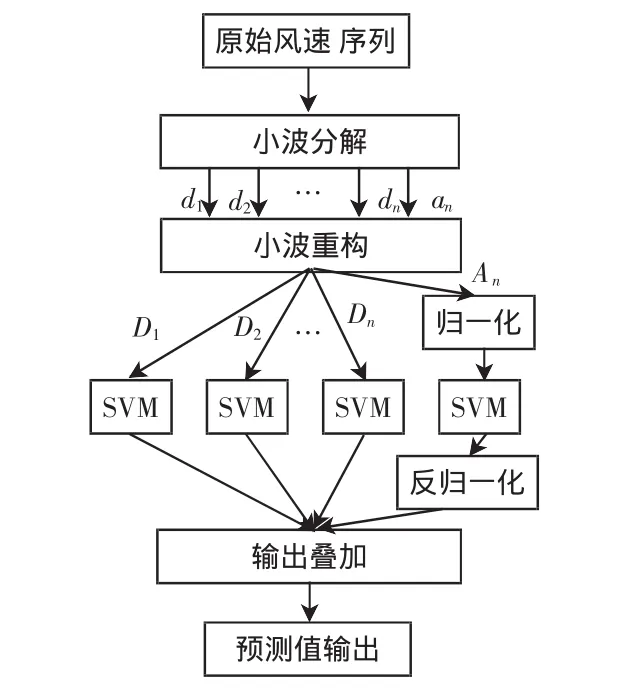
圖1 模型流程Fig.1 Flow chart of the model

2 基于MRA-SVM的風速預測

2.1 模型樣本

在模型的訓練樣本中，合理地選取輸入變量對預測的準確度影響非常大。影響風速變化的因素有很多，如溫度、氣壓、地表等大氣因素，若選取這些變量作為輸入變量，信息的獲取不易，數據量大，運算復雜度增加。因此，風速的預測直接用歷史風速序列來實現。雖然支持向量機模型的復雜度取決于支持向量的個數，并且輸入量的維數越大，預測精度越高，但是輸入維數過大會導致計算存儲量大，計算時間變慢[12]。對于風速序列{x1，x2，…，xn}，令{xi-m，xi-m+1，…，xi-1}為單個的輸入變量，則模型的輸入輸出矩陣為

式中，m為輸入變量維數。綜合考慮計算時間、存儲量、輸入與輸出之間的相關關系，本文取m=8。

本文采用華東地區某風場70m高空的實測風速數據，單位為m/s，該數據為平均每10min采集并存儲1次。選取2012－01－09—2012－01－19期間34號風機的1 448個數據點，即1 440組輸入作為模型的訓練樣本，對未來4 h的24個風速數據進行預測。

2.2 多分辨率分析

多分辨率分析由Mallat引入，從空間概念上形象地說明了小波的多分辨率特性，是信號的塔式多分辨率分析分解與重構的快速算法[13]。

一維情況下離散小波變換的Mallat算法的卷積表達式為

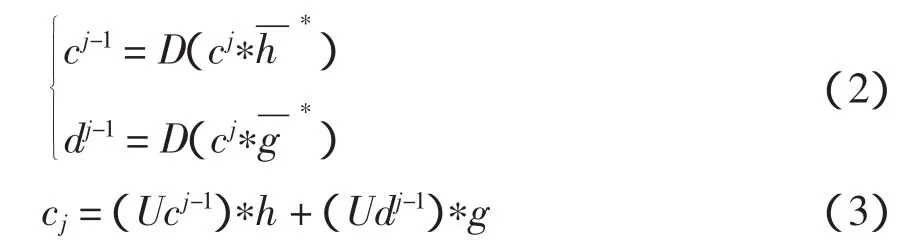
小波分解與重構的迭代過程如圖2所示。

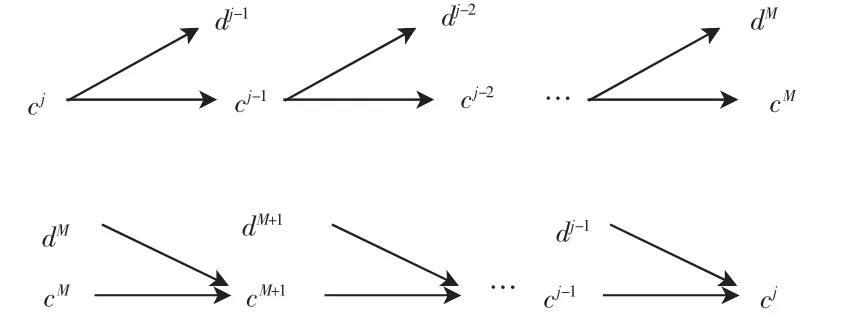
圖2 迭代過程Fig.2 Iterative process

在對風速進行多分辨率分析時，要合理地進行小波基以及分解層數的選擇。選擇不同的小波基將得到不同的分量，而分解的級數過大則需要建立較多的SVM模型對各分量進行預測，各個模型都有一定的誤差，導致最大誤差變大；分解級數過小則不能將原信號不同頻率的信號特征有效地提取出來[5]。因此，從預測計算的時間、算法的復雜度以及誤差等方面考慮，并經過多次實驗驗證后，本文最終選擇db3小波基對原始風速進行3層分解和重構，如圖3所示。

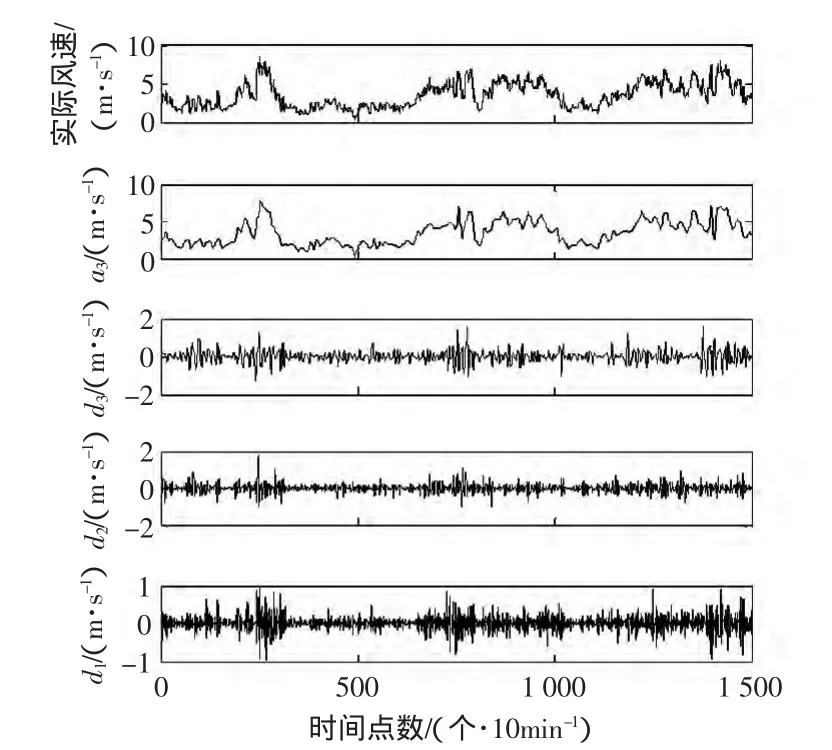
圖3 原始風速序列及小波分解Fig.3 Original wind speed and its wavelet decomposition

2.3 數據歸一化處理

對樣本進行預處理有利于加快算法的收斂速度，提高預測的精度，對訓練集和測試集進行歸一化處理[12]，將原始數據規整在[0，1]范圍內，則有

式中：x、y分別為歸一化前、后的風速序列，x，y∈Rn；xmin=min（x）；xmax=max（x）。歸一化后，yi∈[0，1]，i=1，2，…，n。由于多分辨率分解后的高頻系數幅值較小，因此本文只對低頻部分數據進行歸一化，SVM預測后再進行相應的反歸一化。

2.4 支持向量機

支持向量機由Vapnik首先提出，其主要思想是建立一個分類超平面作為決策曲面，使得正例和反例之間的隔離邊緣被最大化。對于SVM回歸預測，算法將實際問題通過非線性映射轉換到高維的特殊空間，在高維空間中做線性回歸來實現原空間中的非線性回歸。SVM能保證機器具有良好的推廣能力，同時也很好地解決了維數問題，而且其算法復雜度與樣本維數無關。SVM體系結構[7，12]如圖4所示。

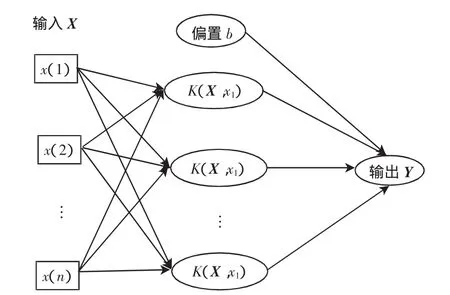
圖4 SVM體系結構Fig.4 Structure of SVM system

對于訓練樣本集{（xi，yi），i=1，2，…，l}，其中xi∈Rn為輸入量；yi∈R為對應的輸出；l為樣本數量。SVM的估計函數為

式中：φ（x）為從輸入控件到高維特征空間的非線性映射；ω為權向量；b為閾值。由最小化風險泛函得到目標函數，即

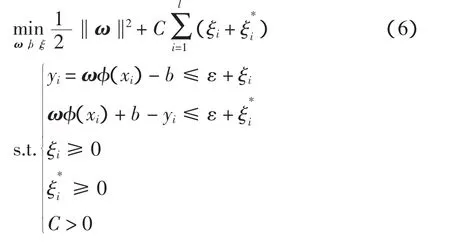
用Lagrange乘子法求解，相應的回歸函數可變換為

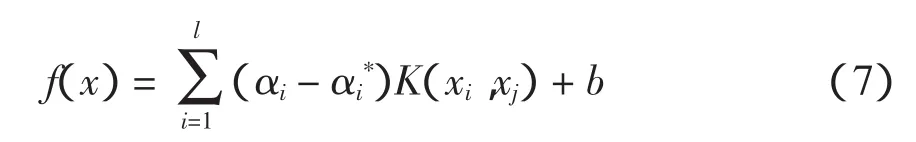
式中：αi、αi*為Lagrange乘子；K（xi，xj）為核函數，且K（xi，xj）=φ（xi）φ（xj）。因此，不需要知道非線性映射φ的具體形式，只要利用核函數就可以進行非線性處理。對于函數回歸問題，其決策函數就是核函數的線性組合，最終問題是尋找一組組合系數（αi-即可[14]。

支持向量機常用的核函數有線性核函數、多項式核函數、徑向基核函數以及高斯核函數等。徑向基核函數具有參數少、數值限制條件少的優點，可降低模型的復雜性。本文采用徑向基RBF核函數，其函數表達式[14]為

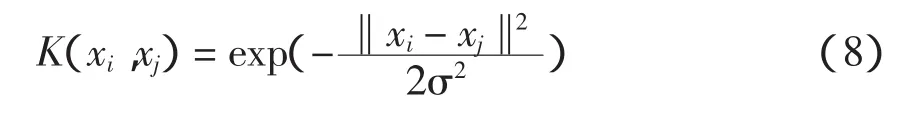
對采集的原始風速數據只進行SVM訓練，輸出回歸預測風速。訓練集的實際風速與預測風速對比如圖5所示。其中，預測均方根誤差eMSE=14.34%，平均絕對百分比誤差eMAPE=9.60%。對未來24 h的風速預測如圖6所示。

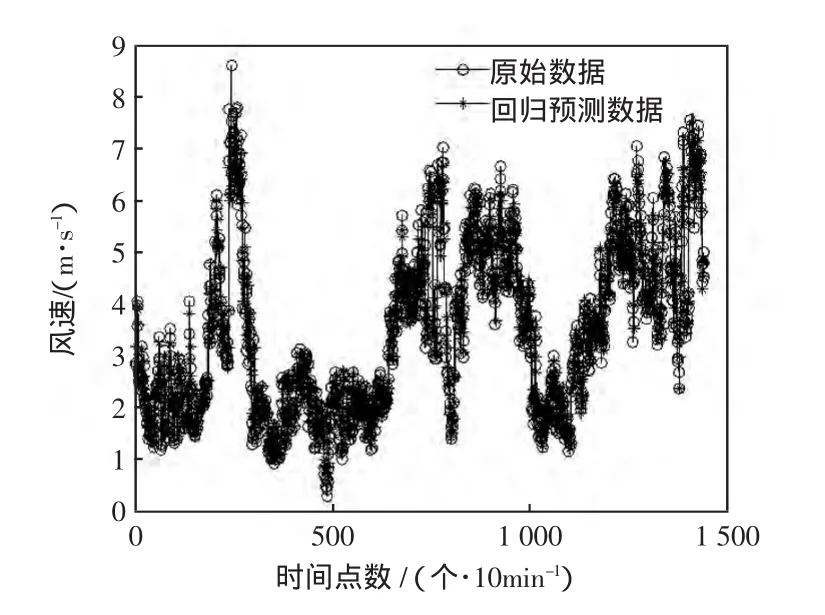
圖5 SVM回歸預測風速Fig.5 Regression forecasting ofw ind speed with SVM

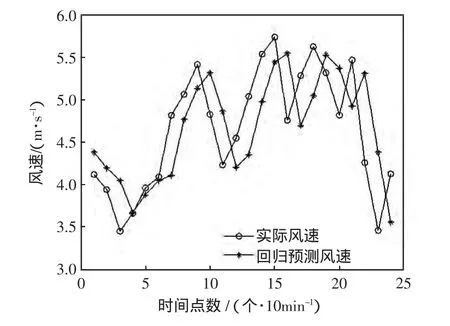
圖6 未來4 h預測風速Fig.6 W ind speed in 4 hours

3 實例分析

3.1 MRA-SVM模型預測

對圖5的原始風速數據進行MRA-SVM預測，當該模型的優化參數與SVM模型的相同時，用圖1的模型結構對風速進行多分辨率分析處理，得到實際數據與回歸預測數據的對比，如圖7所示。其中，預測均方根誤差eMSE=8.46%，平均絕對百分比誤差eMAPE=5.85%。

圖7 MRA-SVM回歸預測風速Fig.7 Regression forecasting ofw ind speed with MRA-SVM

用訓練后的MRA-SVM模型進行對未來4 h的風速進行預測。同時對預測數據與SVM方法進行比較，如圖8所示。

圖8 MRA-SVM與SVM模型的未來24 h風速Fig.8 W ind speed in 24 hours with MRA-SVM and SVM

3.2 評價指標及適應性分析

為了衡量預測風速的精確度，評價MRA-SVM模型的性能，本文采用的均方根相對誤差eRMSE和平均絕對百分比誤差eMAPE分別表示為式中：n為樣本總量；Xi和X^i分別為第i個點的實際風速和預測風速。

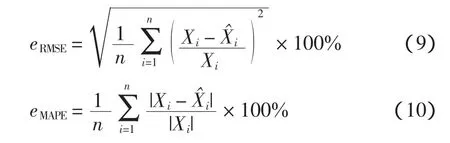
對比2種模型的評價指標，即訓練集與預測集的均方根誤差和平均絕對誤差，結果如表1所示。由表1可知，運用MRA-SVM模型預測風速的eRMSE和eMAPE分別為10.36%、8.81%，與SVM方法的預測指標相比，明顯地提高了風速的預測精度。

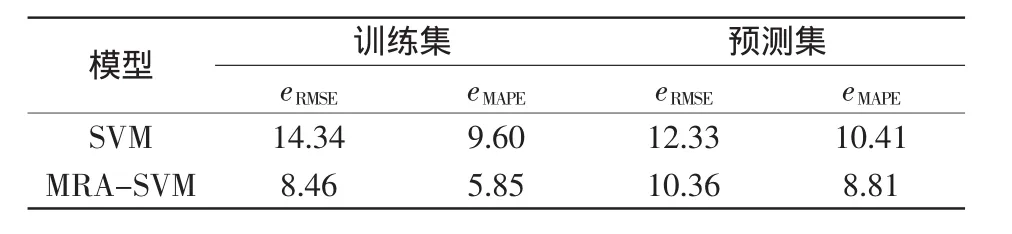
表1 34號風機的SVM及MRA-SVM模型預測指標Tab.1 Prediction index with SVM and MRA-SVM of generator No.34%

為驗證模型是否具有普遍適應性，本文對風場不同的風機在不同時段的風速數據進行實驗，證明回歸預測模型曲線均能較好地跟蹤實際風速曲線。對35號風機的未來4 h的風速進行預測的評價指標如表2所示，由表2可知，用MRA-SVM模型對風速預測的eRMSE和eMAPE分別為16.98%、11.47%，精確度要高于SVM模型的22.18%和17.27%。

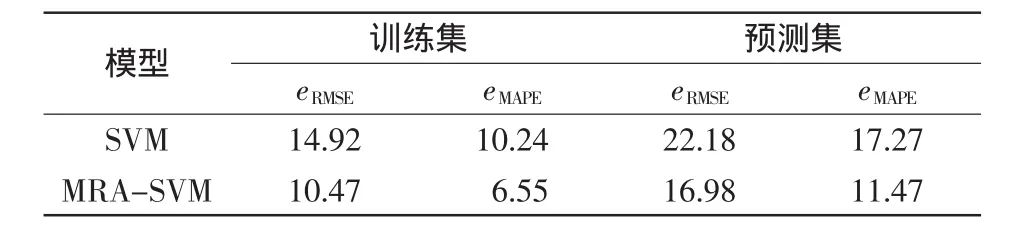
表2 35號風機的SVM及MRA-SVM模型預測指標Tab.2 Prediction index with SVM and MRA-SVM of generator No.35%

通過對不同的數據進行多次實驗證明，該模型能提高預測的精確性，普遍適用于風電場的短期風速預測。

4 結語

針對風電場隨機波動的風速，為提高其預測的準確性，本文運用了MRA-SVM模型對原始風速進行小波分解，降低風速的非平穩性，再運用SVM方法對分解后的近似系數和細節系數分別進行回歸預測并疊加，以此來提高模型的預測能力。通過對風速進行多分辨率分析，用平均絕對百分比誤差和均方根誤差2個指標來評價，預測結果表明，該方法較單獨的SVM方法相比預測效果良好。與此同時，本文對不同的采樣數據進行仿真，驗證了模型的普遍適用性。

[1]楊秀媛，肖洋，陳樹勇（Yang Xiuyuan，Xiao Yang，Chen Shuyong）．風電場風速和發電功率預測研究（Wind speed and generated power forecasting in wind farm）[J].中國電機工程學報（Proceedings of the CSEE），2005，25（11）：1-5．

[2]戴浪，黃守道，黃科元，等（Dai Lang，Huang Shoudao，Huang Keyuan，et al）．風電場風速的神經網絡組合預測模型（Combination forecasting model based on neural net works for wind speed in wind farm）[J].電力系統及其自動化學報（Proceedings of the CSU-EPSA），2011，23（4）：27-31.

[3]羅文，王莉娜（LuoWen，Wang Lina）．風場短期風速預測研究（Short-term wind speed forecasting for wind farm）[J]．電工技術學報（Transactions of China Electrotechnical Society），2011，26（7）：68-74．

[4]李元誠，方廷健，于爾鏗（LiYuancheng，Fang Tingjian，Yu Erkeng）．短期負荷預測的支持向量機方法研究（Study of support vector machines for short-term load forecasting）[J]．中國電機工程學報（Proceedings of the CSEE），2003，23（6）：55-59．

[5]師洪濤，楊靜玲，王金梅，等（Shi Hongtao，Yang Jingling，Wang Jinmei，et al）．基于小波-BP神經網絡的短期風電功率預測方法（A short-term wind power prediction based on wavelet decomposition and BP neural network）[J]．電力系統自動化（Automation of Electric Power Systems），2011，35（16）：44-48．

[6]黃文杰，傅礫，肖盛（HuangWenjie，Fu Li，Xiao Sheng）．采用改進模糊層次分析法的風速預測模型（A predictive model of wind speed based on improved fuzzy analytical hierarchy process）[J]．電網技術（Power System Technology），2010，34（7）：164-168．

[7]吳國旸，肖洋，翁莎莎（Wu Guoyang，Xiao Yang，Weng Shasha）．風電場短期風速預測探討（Discussion about short-term forecast of wind speed on wind farm）[J]．吉林電力（Jilin Electric Power），2005，（6）：21-24．

[8]Sangitab P，Deshmukh SR．Use of support vector machine for wind speed prediction[C]//International Conference on Power and Energy Systems.Chennai，India：2011．

[9]Zeng Deliang，Liu Yu，Liu Jiwei，et al．Short-term wind speed forecasting based on wavelet tree decomposition and support vector machine regression[J]．Advances in Automation and Robotics，2011，123（2）：373-379．

[10]張彥寧，康龍云，周世瓊，等（Zhang Yanning，Kang Longyun，Zhou Shiqiong，et al）．小波分析應用于風力發電預測控制系統中的風速預測（Wavelet analysis applied to wind speed prediction in predicate control system of wind turbine）[J]．太陽能學報（Acta Energiae Solaris Sinica），2008，29（5）：520-524．

[11]王曉蘭，王明偉（Wang Xiaolan，WangMingwei）．基于小波分解和最小二乘支持向量機的短期風速預測（Short-term wind speed forecasting based on wavelet decomposition and least square support vector machine）[J]．電網技術（Power System Technology），2010，34（1）：179-184．

[12]彭春華，劉剛，孫惠娟（Peng Chunhua，Liu Gang，Sun Huijuan）．基于小波分解和微分進化支持向量機的風電場風速預測（Wind speed forecasting based on wavelet decomposition and differential evolution-support vector machine for wind farms）[J]．電力自動化設備（Electric Power Automation Equipment），2012，32（1）：9-13．

[13]劉輝，田紅旗，李燕飛，等（Liu Hui，Tian Hongqi，LiYanfei，et al）．基于小波分析法與滾動式時間序列法的風電場風速短期預測優化算法（Short-term forecasting optimization algorithm for wind speed from wind farms based on wavelet analysis method and rolling time series method）[J]．中南大學學報：自然科學版（Journal of Central South University：Science and Technology），2010，41（1）：370-375．

[14]Zhang Huaqiang，Wang Xinsheng，Wu Yinxiao．Application of an improved SVM algorithm for wind speed forecasting[J]．Future Intelligent Information Systems，2011，86（1）：333-340．