實際負荷變化模式下的靜態電壓穩定分析

伍利，南海鵬，姚李孝

（西安理工大學水利水電學院，西安 710048）

由于環境和經濟的因素，電力系統運行越來越靠近其穩定極限[1～4]。對于一個實際系統而言，負荷增長受很多因素的影響，通常在電力系統分析中，可以將負荷的變化看作不確定的擾動。在計算靜態電壓穩定裕度指標的過程中，選擇負荷增長的模式是一個難點，不同的負荷增長模式對靜態電壓穩定裕指標大小的影響很大。在采用負荷等比例等功率因數增長的模式下，整個系統的靜態電壓穩定裕度可能受制于這些電壓穩定弱節點集。這一方面反映了真實系統中的薄弱母線和薄弱區域，另一方面，這樣的結果還不能給出一個完全貼近系統真實情形的裕度值，因為在實際系統中，負荷往往并非按等比例等功率因數方式增長。更合理的模式應參考實際電網的負荷預測數據，由負荷預測數據給出一個合理的負荷增長方向，根據負荷預測增長方向計算的負荷裕度應該比等比例負荷增長模式下的負荷裕度更加貼近電網運行實際情況[4～8]。

系統的負荷裕度為當前運行點的負荷水平和電壓穩定極限點的負荷水平之間的差值，即系統所處的運行狀態不同，系統的負荷裕度不同。從基值開始的不同負荷增長率叫做負荷增長模式或負荷變化方向LD（load direction），負荷增長模式是不可控制的。已有的研究成果大多只是簡單分析了負荷增長對電壓穩定的影響，沒有對負荷增長模式對電壓穩定裕度的影響進行細化研究。根據系統當前的運行狀態及該地區負荷的增長模式分析的電壓穩定才能對系統的實際運行作指導。通常一天的負荷變化由日負荷曲線表示，在靜態電壓穩定分析中用日負荷曲線識別負荷的增長模式，就能預測當前系統運行狀態下的負荷裕度。

本文以歷史負荷數據為依據，對負荷數據進行模糊聚類分析，然后用改進的BP神經網絡進行負荷預測，確定負荷的增長模式及負荷的變化方向，在此基礎上用連續潮流法對IEEE30進行電壓穩定研究分析，獲得系統在當前運行狀態及一定負荷增長模式下的系統電壓穩定裕度。

1 負荷增長

負荷增長模式或“方向”定義為系統中每個節點負荷增長的方式，即

式中：PDi0、QDi0分別為節點i（i=1，2，…，n）的有功、無功基礎負荷；PDi、QDi分別為節點i的有功、無功負荷；λ為負荷增長因子，表示有功和無功以相同比率增長，也就是負荷在相同的功率因數下增長；KDi為節點有功和無功負荷增長的方向標量，并且對電壓穩定有影響。

傳統方法算法中，負荷以相同的比例增長[7～10]。在考慮負荷增長模式的電壓穩定研究中，潮流等式被修正為含有負荷增長因子及負荷方向的標量，即

式中：KD為負荷變化方向矢量，在文獻[3]中，節點2和節點3的基礎負荷分別為21.70+j12.7MV和94.2+j19.00MV。在節點2取KD2=0.217+j0.127；在節點3取KD3=0.942+j0.19。也就是對于一個負荷因子λ，負荷節點將以相同的百分數從基值增長，但各節點的負荷增長模式不同。文中對以相同負荷增長率的稱其為相同的負荷方向或傳統的負荷方向。

2 預測模型及算法

2.1 形成預測樣本

計算靜態電壓穩定裕度指標的短期負荷預測是電力系統安全經濟運行的基礎，負荷預測受到各種因素的影響，如氣象因素、日類型和突發事件等。氣象因素有氣溫、濕度、降雨量和風速等，日類型包含有一般工作日、雙休日和特殊節假日。對這些相關因素的規范處理，可提高短期負荷預測的精度。

設預測日的n個樣本集為X=[x1，x2，…，xn]T，每個樣本xj有m個特征指標xj=[xj1，xj2，…，xjm]T（j=1，2，…，n），則n個樣本的特征指標為

樣本與樣本之間的模糊相似關系矩陣為

在一定條件下樣本集X通過模糊關系矩陣R進行分類。對X=[x1，x2，…，xn]T分成c類（2≤c≤n），則c個聚類中心向量為

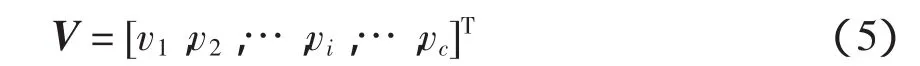
vi（i=1，2，…，c）對應的m個指標是該類元素所對應的平均值，vi=（vi1，vi2，…，vim]，則

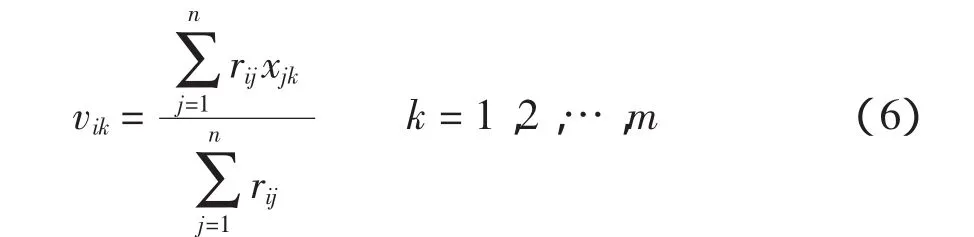
式（6）的分母相當于第i類的元素個數，而分子為第類的所有元素第k個指標和。為了獲得一個最佳的模糊分類，可通過模糊聚類算法迭代運算，優選一個最好的模糊分類，即

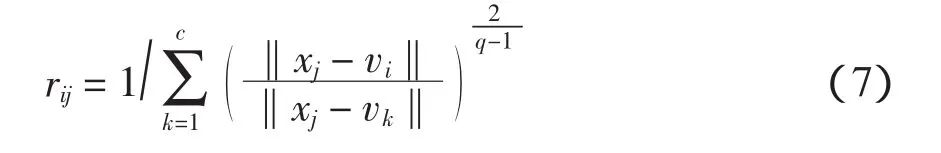
式中：q=2；‖xj－vi‖為Euclid距離。

2.2 預測日歸類

樣本進行分類后，對預測日進行歸類，歸類時需計算預測日與樣本類別的歐氏距離，即

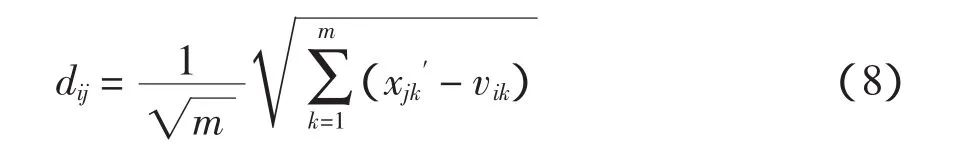
式中，xjk′為預測日的特性指標，以最短歐氏距離作為預測日的歸類判別，然后以BP網絡進行預測。

2.3 改進BP神經網絡預測模型

BP算法是一個非線性梯度最優問題，存在收斂速度慢和易陷入局部極小值。改進的BP神經網絡[6]采用附加動量法以改變每次迭代的前進方式來提高收斂速度。附加動量算法是在梯度下降的基礎上，引入動量因子η（0＜η＜1）能使網絡收斂得更快，并且可避免局部極小值的出現。

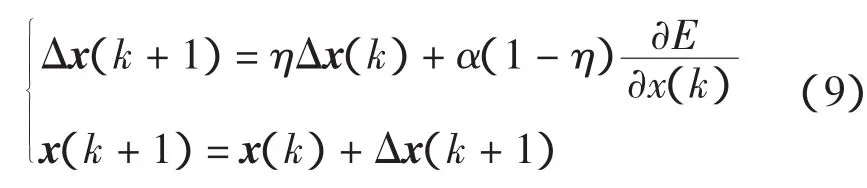
式中：x（k+1）、x（k）分別為第k+1、k次迭代時的權值向量；α為學習速率。

該方法所加入的動量項是指在網絡每次的權值和閾值改變量中加入前一次的改變量，并且動量因子η越大，同一梯度方向上的動量也越大。實質上動量項相當于阻尼項，它減少了學習過程的振蕩趨勢，改善了收斂性。上述表明在保證算法穩定的同時，附加動量法的收斂速率較快，學習時間較短。

3 電力系統日負荷曲線及負荷預測

3.1 日負荷曲線

實際的系統負荷是隨時間變化的，其規律可用負荷曲線來描述。常用的負荷曲線有日負荷曲線和年負荷曲線。日負荷曲線是以1 d（24 h）為周期的負荷變化。隨著我國電力市場的進一步發展，日負荷曲線對電力系統的運行非常重要，它是安排日發電計劃和確定系統運行方式的重要依據。從負荷曲線可知，日負荷會出現早高峰和晚高峰，冬季的早高峰出現在10：00左右，晚高峰出現在19：00左右。而夏季的早高峰略有提前，出現在9：00左右，午后的負荷高峰在16：00左右，晚高峰略有推遲，出現在21：00左右。早高峰低于午后高峰和晚高峰，最大負荷出現在晚高峰時段。各高峰之間負荷變化有明顯的波動，在早、晚高峰之間負荷持續在高峰。

3.2 負荷預測

一個地區的負荷變化取決于多種因素，如氣溫、人的行為、負荷類型、關稅等等，這可從不同地區的實際日負荷需要反映出來。在這些因素的影響下，不同地區的電力系統的短期負荷會出現較大的差異[6～11]。本文先將影響負荷變化的主導因素進行分析，也就是對氣象因素和日類型與負荷之間的關系進行量化處理，建立模糊相似矩陣。采用模糊聚類方法對夏季負荷類型進行分析并形成預測樣本，然后對預測日以最短歐氏距離進行歸類，再對1 d的24點負荷逐點建立BP神經網絡預測模型，用附加動量和變學習速率的BP算法訓練樣本，最終得到預測日24點的負荷值，預測結果如表1所示。

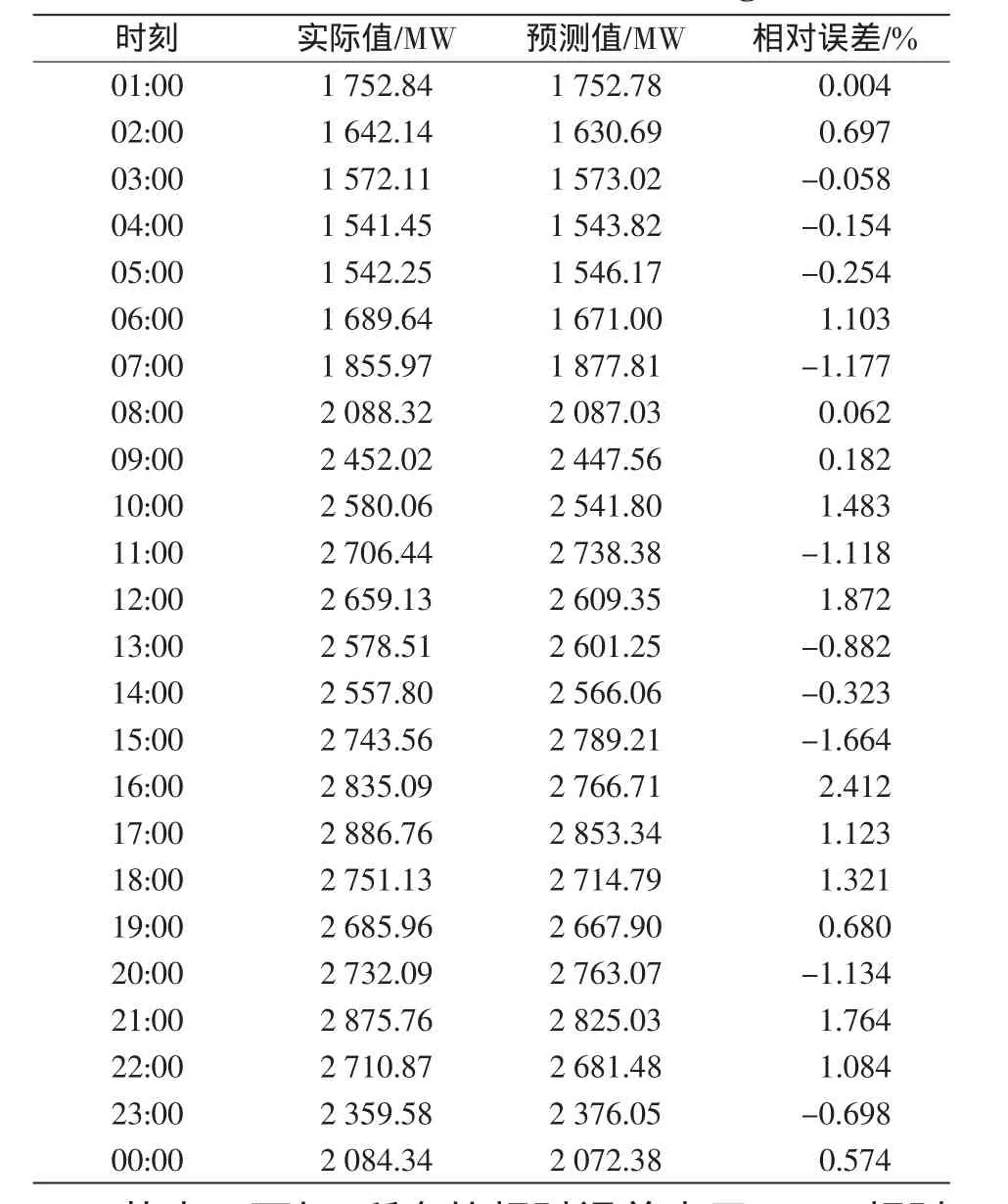
表1 負荷預測結果Tab.1 Resultsof load forecasting

從表1可知，所有的相對誤差小于3%。相對誤差小于2%的點有23個，最大相對誤差為2.412%，最小相對誤差為－0.058%，平均相對誤差0.317%，預測值符合實際負荷變化。

在經典的電壓穩定研究中，應用相同的負荷方向不符合實際的電力系統，在日負荷的不同時間每一節點的負荷增長模式由日負荷曲線確定，即

式中：Pm，t+1為t+1時刻的負荷預測數據；Pm，t為t時刻的負荷預測數據。不同時段的負荷變化如表2所示，Pm，max為Pm，t的最大值。

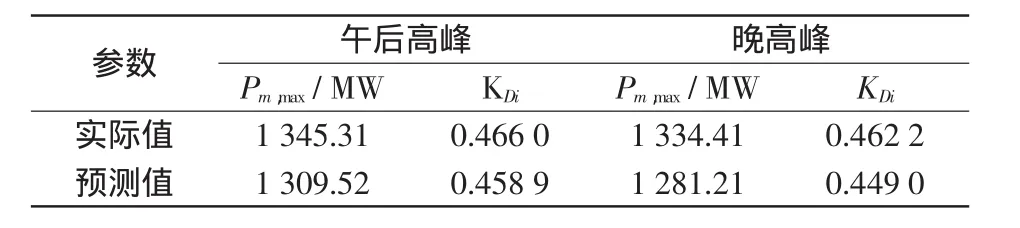
表2 不同時段負荷變化方向Tab.2 Load variation direction in different time

由于負荷預測只提供有功功率預測，以維持功率因數恒定，在計算中假定無功功率也以相同的系數增加。因此，在連續潮流等式（2）中系統負荷節點的無功率負荷增量由式（1）獲得。

4 結果分析

本文以IEEE30系統為例，如圖1所示，分別以傳統負荷增長模式和預測負荷增長模式將增長負荷在可利用的發電機間進行分配，以CPF進行潮流分析，計算系統的負荷裕度，獲得各節點的PV曲線。選取在負荷增加時節點電壓較弱并對負荷變化敏感的節點3、4、6、7、9和節點10進行比較[11～16]，如圖2和圖3所示。

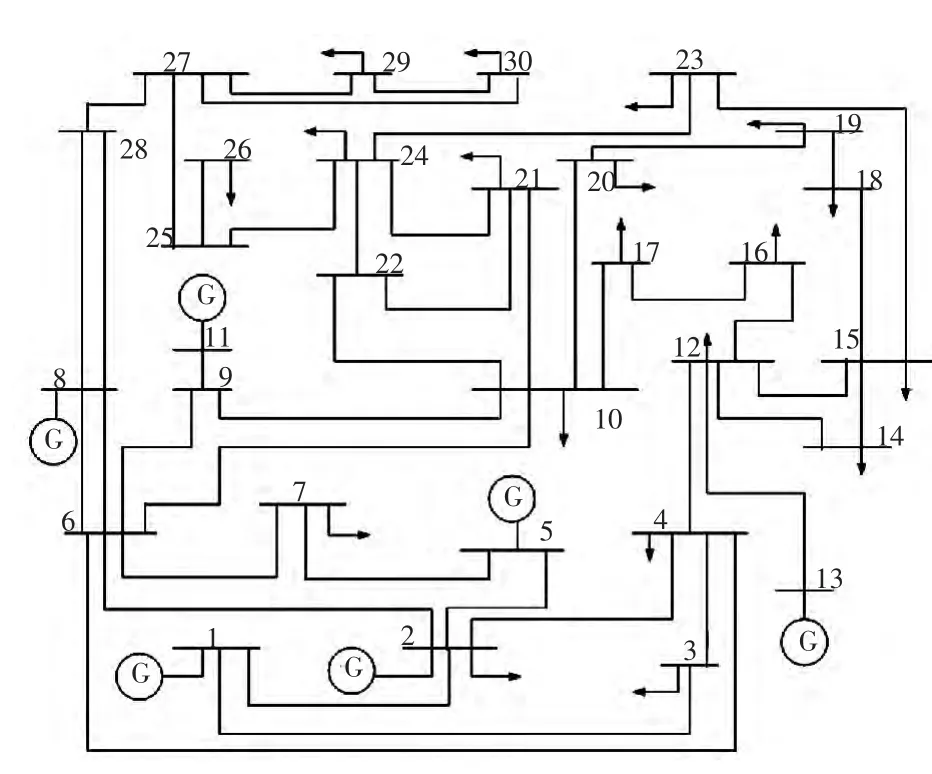
圖1 IEEE30測試系統Fig.1 IEEE30 test system

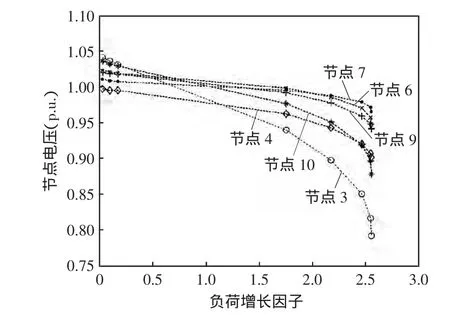
圖2 傳統負荷增長時較弱節點的電壓Fig.2 Bus voltage of weak nodes with conventional load grow th

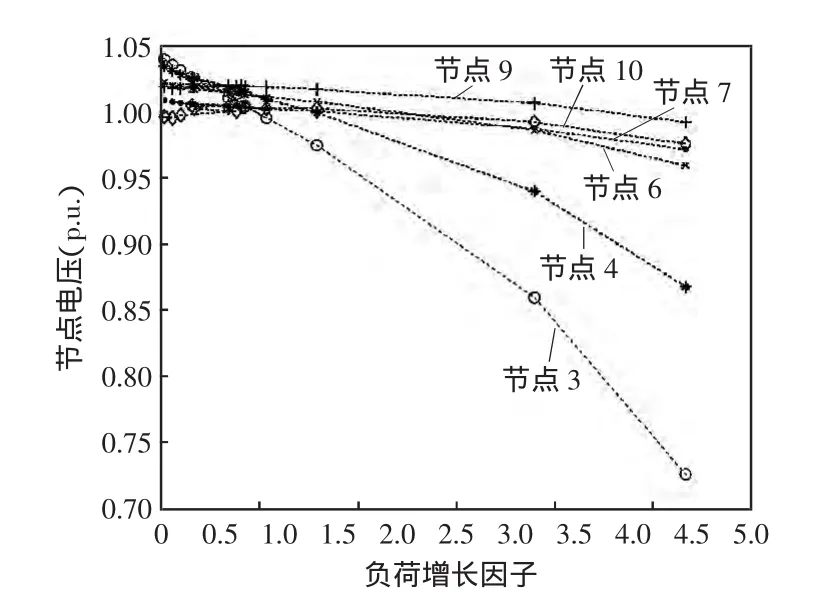
圖3 基于預測負荷增長時較弱節點的電壓Fig.3 Bus voltage of weak nodes based on forecasted load grow th

由圖2和圖3可知負荷增長模式不同對較弱節點的電壓及系統負荷裕度的不同影響，節點6、7、9、10電壓軌跡變化顯著。在圖2中傳統相同負荷增長模式下負荷增值較大，負荷增長因子小，潮流結果變化顯著，在PV曲線接近鼻型區域損耗增加較快，因此負荷裕度小。在圖3中預測負荷增長模式負荷增值相對較小，負荷增長因子大，潮流結果開始變化較小，在接近其裕度極限時，電壓下降加快，電壓下降了8.2%，但負荷裕度相比提高了55%。

表3給出了系統不同運行階段的LD及其負荷裕度，可知在晚高峰時，負荷裕度高于在午后高峰，主要是由于晚高峰時段各負荷節點的負荷功率已經處于高峰，系統再能承受的的負荷增長很有限。

表3 不同LD的負荷裕度比較Tab.3 Load margin comparison of different LD（p.u.）

5 結論

本文以采集的典型日負荷曲線預測未來時段內負荷的變化，應用CPF對以此確定的負荷增長模式進行電壓穩定分析。以實際負荷增長模式評估靜態電壓穩定的特點。

（1）以實際歷史負荷樣本預測負荷增長模式能真實反映電力系統負荷增長方式。

（2）采用模糊聚類和改進的BP神經網絡模型預測的負荷增長相對誤差小于3%，符合實際的負荷增長規律。

（3）與傳統分析靜態電壓穩定分析相比，系統所處的運行狀態不同，系統可承受的負荷增長不同，因而系統的負荷裕度不同；不同負荷增長模式使系統各節點的PV曲線呈現不同的變化。在系統的峰荷時段，系統能承擔的負荷增長是有限的。以本文方法對系統的不同運行狀態的電壓穩定分析，對電力系統調度有一定的實際指導意義。

[1]Nagao T，Tanaka K，Takenaka K．Development of static and simulation programs for voltage stability studies of bulk power system[J]．IEEE Trans on Power Systems，1997，12（1）：273－281．

[2]Sode Y A，Mithulananthan N，Lee K Y．Effect of realistic load direction in static voltage stability study[C]//IEEE/PES Transmission and Distribution Conference and Exhibition.Dalian，China：2005．

[3]Green S，Dobson I，Alvarado F L．Sensitivity of loading margin to voltage collapse with respect to arbitrary parameters[J]．IEEE Trans on Power Systems，1997，12（1）：262-272．

[4]Sode Y A，Mithulananthan N．Maximizing static voltage stability margin in power systems using a new generation pattern[J].Australian Journal of Electrical&Electronics Engineering，2005，2（3）：255-261．

[5]栗然，曹磊，李莉，等（LiRan，Cao Lei，Li Li，et al）.影響電力系統短期負荷預測因素的權重分析方法（Analysis for weights allocation with influence factors in power system short-term load forecasting）[J].華北電力大學學報（Journal of North China Electric Power University），2007，34（5）：32-37．

[6]姚李孝，宋玲芳，李慶宇，等（Yao Lixiao，Song Lingfang，LiQingyu，et al）．基于模糊聚類分析與BP網絡的電力系統短期負荷預測（Power system short-term load forecasting based on fuzzy clustering analysis and BP neural network）[J].電網技術（Power System Technology），2005，29（1）：20-23．

[7]黎燦兵，李曉輝，趙瑞，等（LiCanbing，LiXiaohui，Zhao Rui，et al）．電力短期負荷預測相似日選取算法（A novel algorithm of selecting similar days for short-term power load forecasting）[J]．電力系統自動化（Automation of Electic Power Systems），2008，32（9）：69-73．

[8]黎燦兵，楊朋，劉瑋，等（LiCanbing，Yang Peng，Liu Wei，et al）．短期負荷預測中考慮夏季氣溫累積效應的方法（An analysis of accumulative effect of temperature in short-term load forecasting）[J]．電力系統自動化（Automation of Electric Power Systems），2009，33（9）：96-99．

[9]高新波．模糊聚類分析及其應用[M].西安：西安電子科技大學出版社，2004.

[10]陳得治，張伯明，方興（Chen Dezhi，Zhang Boming，Fang Xing）．節點注入功率模式對電壓穩定裕度的影響（Effect nodal injection power mode on voltage stability margin）[J]．電網技術（Power System Technology），2009，33（2）：62-67，72.

[11]隨慧斌，趙建國，李可軍，等（SuiHuibin，Zhao Jianguo，LiKejun，et al）．考慮不均衡區域負荷增長的在線電壓穩定評估（On-line voltage stability assessment considering uneven growth of regional load）[J]．電力自動化設備（Electric Power Automation Equipment），2011，31（3）：57-61．

[12]趙晉泉，張伯明（Zhao Jinquan，Zhang Boming）．連續潮流及其在電力系統靜態穩定分析中的應用（Summarization of continuation power flow and its application in static stability analysis of power system）[J]．電力系統自動化（Automation of Electric Power Systems），2005，29（11）：91-97．

[13]熊寧，程浩忠，李曼麗，等（Xiong Ning，Cheng Haozhong，LiManli，et al）．基于可信度區間的靜態電壓穩定性評價（A static voltage stability evaluation method based on confidence intervals）[J]．電力系統自動化（Automation of Electric Power Systems），2009，33（9）：16-19．

[14]顧偉，蔣平，唐國慶（GuWei，Jiang Ping，Tang Guoqing）．提高電力系統小擾動穩定性的最優分岔控制策略（Optimal bifurcation control to improve small-signal stability of power systems）[J]．電力自動化設備（Electric Power Automation Equipment），2007，27（10）：29-33．

[15]伍利，古婷婷，姚李孝（Wu Li，Gu Tingting，Yao Lixiao）．基于改進連續潮流法的靜態電壓穩定分析（Static voltage stability analysis based on improved continuation power flow）[J]．電網技術（Power System Technology），2011，35（10）：99-103．

[16]張堯，張建設，袁世強（Zhang Yao，Zhang Jianshe，Yuan Shiqiang）．求取靜態電壓穩定極限的改進連續潮流法（Improved continuation power flow algorithm for obtaining the limit of static voltage stability）[J]．電力系統及其自動化學報（Proceedings of the CSU-EPSA），2005，17（2）：21-25．