淺談分數應用題的解法

張克

稍復雜的求一個數的幾分之幾是多少的應用題和已知一個數的幾分之幾是多少，求這個數的應用題是小學階段最抽象、學生最難理解的數學知識之一，也是學生最容易混淆的內容之一。怎樣幫助學生學好分數應用題，是擺在我們數學教師面前的一項重要任務，我們必須認真鉆研教材，領會教材的編寫意圖，鼓勵學生積極參與教學活動，真正使學生學會、理解稍復雜的分數應用題的解法。

一、讓學生用不同思路解答稍復雜的分數應用題，使解題方法多樣化

為了便于比較，以下面兩道題為例來說明：

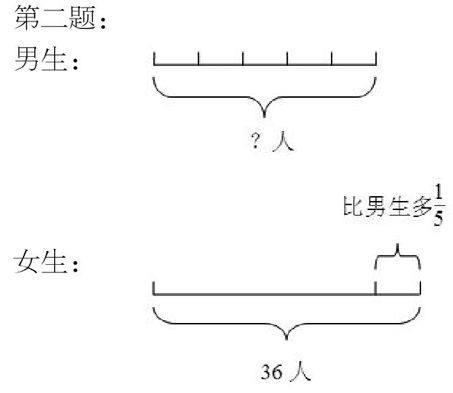
（1）4年（1）班有男生30人，女生比男生多1/5 ，女生有多少人？

（2）4年（2）班有女生36人，比男生多1/5 ，男生有多少人？

1. 用解整數應用題的思路來解分數應用題。

（1）出示上面兩道題，讓學生說說這兩道題有什么相同點和不同點。

相同點：這兩道題都是把男生人數看作單位“1”，兩道題的第二個條件相同。

不同點：第一題單位“1”的量是已知的，第二題單位“1”的量是未知的。

（2）畫線段圖分析

第一題：

男生：

把男生人數看作單位“1”，則可列出等式：男生人數加上女生比男生多的人數等于女生人數。即：男生人數+男生人數×1/5 =36，然后列方程解答。解：設男生有X人，X+ 1/5 X=36，X=30。

用解整數應用題的思路解分數應用題是從學生已有的知識和經驗出發來學習新知識，符合學生的認知規律，便于學生接受和理解新知識。

2. 用較新的思路來解分數應用題。第一題：把男生人數看作單位“1”，女生人數相當于男生人數的（1+ 1/5 ），求女生有多少人，就是求30人的（1+ 1/5 ）是多少，列式為30×（1+ 1/5 ）=36（人）

第二題：把男生人數看作單位“1”，女生人數相當于男生人數的（1+ 1/5 ），也就是男生人數的（1+ 1/5 ）是女生人數，即：男生人數×（1+ 1/5 ）=36，根據這個等式可以列方程解答。解：設男生有X人，（1+ 1/5 ）X=36，X=30;也可以根據除法的意義用算術方法解，36÷（1+ 1/5 ）=30（人）。

這是一種比較新的思路，它是建立在一個數乘以分數的意義的基礎之上的，只要學生理解了一個數乘以分數的意義，也就能夠理解這種解題思路。

3. 用整數列式解分數應用題。第一題：把男生人數看作單位“1”，把男生人數平均分成5份，則女生人數比男生多1份，即5+1=6份，先求1份有多少人，再求6份有多少人，列式為30÷5×（5+1）=36（人）。

第二題：分析同上題，先求1份有多少人，再求5份有多少人，列式為36÷（5+1）×5=30（人）。

這種解題思路雖然不是教材所提倡的，但是對一些學困生來說學會這種解題思路也是有益的。

二、抓住兩種類型分數應用題之間的內在聯系，巧解分數應用題

從上面兩道題可以看出，兩種類型分數應用題具有相同的基本結構，只不過是已知條件和所求問題變化了，二者的解題思路基本上是一致的，它們具有共同點，是一個數乘以分數的意義，把二者聯系起來，因此我們在教學中要引導學生分析這兩種類型分數應用題中的數量關系，弄清它們之間的內在聯系，進而從整體上把握其解題規律。

如從第一題和第二題的第二個條件中，都能很容易得出這樣的數量關系，男生人數+男生人數×1/5 =女生人數，或男生人數×（1+ 1/5 ）=女生人數，然后把已知條件分別代入上面的等式中。即：

第一題：30+30×1/5 =女生人數，或30×（1+ 1/5 ）=女生人數，這樣可以直接求出女生人數。

第二題：男生人數+男生人數×1/5 =36，或男生人數×（1+ 1/5 ）=36，根據這兩個等式可以列方程或用算術方法求出男生人數。

通過上面對兩道題的分析可知：任何一道求一個數的幾分之幾是多少的應用題和已知一個數的幾分之幾是多少，求這個數的應用題，都可以寫成一個具體的數量關系式，然后把已知條件代入關系式中，便能求出答案。

三、交給學生通俗易懂的解題方法，切忌死記硬背

有的教師在教學上面的兩種類型應用題時，常常引導學生總結所謂的解題方法，即：如果單位“1”的量是已知的用乘法列式;如果單位“1”的量不是已知的，列方程或用除法列式。

這是交給學生一種死記硬背的解題方法，一部分學生特別是學困生并沒有理解，只能暫時記住這種方法，過一段時間這樣的題又開始混淆了，顯然這樣的教學是不成功的。

我們在教學中應結合學生的學習活動，引導學生總結出通俗易懂的解題方法，使學生不但會用而且會講，說出其來源，這樣學生才是真正地理解了所學知識。

總之，我們在教學中應不斷的更新教育觀念，改革教學方法，積極引導學生參與教學活動，讓學生概括應用題的解題規律，總結解題方法，并知其來龍去脈，真正使學生靈活自主地學習數學知識。