數學例題教學之我見
王俊
【摘要】 例題的選取要緊扣本節課的知識目標,例題的選取要貼近學生的生活. 在例題教學中,要注意例題的引申和推廣,在例題教學中,要充分調動學生的積極性,發揮學生的主體作用,挖掘課本例題,發揮課本例題的作用.
【關鍵詞】 例題的重新加工;例題的引申;學生的主體作用;學生的思維;解題方法
例題是數學教材的重要組成部分,是教材的主要內容,是學生鞏固基礎知識、掌握解題思想方法的主要渠道,對培養學生良好的思維品質,對學生的能力培養起著非常重要的作用,是大面積提高數學教學質量的重要環節. 這就要求教師認真備課,充分發揮例題的作用. 下面我談一下關于例題教學的五點見解.
一、例題的選取,要緊扣本節課的知識目標
數學課堂上一般是先進行知識點的教學,然后再進行例題的教學. 進行例題教學的目的是為了讓學生掌握知識點的運用,因此,備課時要反復研究所設例題的內容是否緊扣本節課的知識點、數學思想及數學方法等. 例如人教版八年級數學上冊“14.3.3一次函數與二元一次方程(組)”這一節,教材上設計了一道例3:
一家電信公司給顧客提供兩種上網方式:方式A以每分0.1元的價格按上網時間計費;方式B除收月計費20元外再以每分0.05元的價格按上網時間計費. 上網時間為多少分,兩種方式的計費相等?
就例3來看,列一元一次方程是完全能解答的問題,并且這種解法非常簡單. 但教材安排例3的真正目的,是用函數方法來解. 因此,我在備課時對此例題進行了重新加工. 在已知條件不變的前提下,設計了以下五個問題:
(1)寫出兩種方式的收費y(元)與上網時間x(分)之間的函數關系式.
(2)在同一平面直角坐標系中畫出函數的圖像.
(3)求函數圖像的交點坐標.
(4)上網時間為多少分時兩種方式的計費相同?
(5)顧客應如何選擇上網方式更經濟?
這樣重新設計后,它就是一道完整的函數題了,并且緊扣本節的知識目標和方法. 當然,不這樣設計,硬用函數方法也能講,但是學生是不會認可的,會認為沒有必要.
二、例題的選取要貼近學生的生活
例題的選取要貼近學生的生活,是為學生所熟悉的內容,這樣不僅可以激發學生的學習熱情,還能發揮學生的創新意識和創造能力,從而增強學生學習數學的興趣,有利于提高教學效果. 例3就是學生所熟悉的內容,貼近學生的生活,學生不僅用函數知識把問題解答了,而且進一步加深了對一次函數、一元一次方程、二元一次方程(組)、一元一次不等式的關系的認識.
三、在例題教學中,要注意例題的引申和推廣
在例題教學中,要注意例題的推廣和引申. 推廣引申就是解完例題后,對原例題的條件、結論、題型作進一步的開拓思考,引申出新題和新的解法. 世界上的事物都是不斷變化的,數學各知識之間也是相互依存、互相制約、不斷變化的. 對例題進行推廣引申,有利于把知識講活,也有利于知識之間的內在聯系,對培養學生的數學思維是大有益處的.
例如人教版八年級數學上冊“14.3.3一次函數與二元一次方程(組)”這一節教材上的例3:一家電信公司給顧客提供兩種上網方式:方式A以每分0.1元的價格按上網時間計費;方式B除收月計費20元外再以每分0.05元的價格按上網時間計費. 上網時間為多少分,兩種方式的計費相等?
就本題而言,所求的問題是上網時間為多少分,兩種方式的計費相等,可以把此問題進一步深化:顧客應如何選擇上網方式更經濟?
四、在例題教學中,要充分調動學生的積極性,發揮學生的主體作用
在例題教學中,要以學生為主體,給學生充分的活動時間,盡可能多地靠學生自己發現解題思路和動手作答. 可以通過小組合作、小組展示、學生點評來完成. 教師不要把例題的解法直接講給學生,要充分相信學生,讓學生在努力學習的過程中、在小組合作學習的過程中,實現學習目標,讓學生獲得成功的快樂. 學生親自動手實踐獲取的知識,比老師講授印象要深,記憶要牢固,更不容易遺忘. 有些老師經常說:這道題我都講了四五遍了,學生還是不會. 我想,不妨你不講,讓學生親自動手試試.
五、挖掘課本例題,發揮課本例題的作用
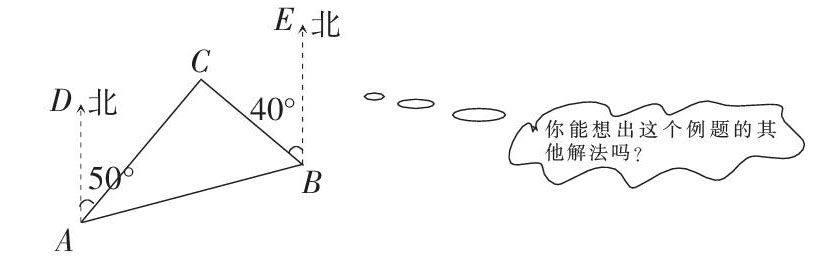
對課本上的例題,要認真挖掘,發揮好教材上例題的作用,尤其是一題多解和多題一解的例題更應給予高度重視. 因為通過一題多解、多題一解例題的教學,能夠提高學生的思維能力、創新能力、分析問題和解決問題的能力, 能調動學生積極思維,提高學生的學習積極性. 例如人教版八年級數學上冊第12頁的例2:如圖,C島在A島的北偏東50°方向,B島在A島的北偏東80°方向,C島在B島的北偏西40°方向.從C島看A,B兩島的視角∠ACB是多少度?
在課堂教學中,同學們通過小組合作學習,在課本解法的基礎上又研究出了多種其他解法(例如:經過點C作CH∥BE;經過點C作MN∥AB;延長AC交BE于G等),有的小組還發現如果不給出“B島在A島的北偏東80°方向”這一條件,也可以求出∠ACB的度數. 通過這節課的學習,同學們不僅能夠靈活運用三角形內角這一節課的知識解決問題,而且鞏固了平行線的性質等知識,還探索出添輔助線的方法,同時,也提高了學生分析問題、解決問題的能力,豐富了學生們的解題方法. 你說,這道例題不是很好嗎?

