軸對稱雙喉道氣動矢量噴管內特性數值模擬

卿太木，王 恒，廖華琳

(中國燃氣渦輪研究院，四川 成都 610500)

1 引言

推力矢量技術被認為是第四代戰斗機和先進無人作戰飛機的必備技術，有著巨大的軍事和經濟意義。氣動矢量噴管作為推力矢量技術的代表，已成為替代現役和在研機械調節式矢量噴管的革命性技術方案，引起了國內外廣泛重視。雙喉道氣動矢量噴管，是美國NASA蘭利研究中心于2003年提出的一種新型氣動矢量噴管概念[1]。蘭利研究中心對二元雙喉道氣動矢量噴管的幾何結構參數、噴管主/次流進口參數變化對噴管內特性的影響，進行了數值模擬和模型試驗研究[2]，找出了二元雙喉道氣動矢量噴管內特性變化規律。國內對氣動矢量噴管也進行了一定研究，文獻[3]對二元雙喉道氣動矢量噴管的幾何結構參數變化進行了數值仿真分析，文獻[4]對軸對稱雙喉道氣動矢量噴管的進口氣動參數進行了數值仿真分析。本文利用數值模擬方法，對軸對稱雙喉道氣動矢量噴管幾何參數變化對噴管內特性的影響進行了分析，并優選了一組噴管幾何結構參數。

2 計算模型及內特性參數定義

2.1 計算方法

軸對稱雙喉道氣動矢量噴管計算幾何模型見圖1。采用經文獻[4]驗算過的FLUENT三維解算器基于有限體積法進行耦合求解，計算模型選用基于湍流能量方程和擴散速率方程的標準兩方程k-ω模型，對流項選用二階迎風差分格式，時間項采用全隱式。圖中，D7為噴管進口直徑，D8為噴管喉道直徑，D9為噴管出口直徑，L為噴管空腔長度，α為次流注入角度，θ1為空腔擴張角，θ2為空腔收斂角，β為次流周向角，d為次流小孔直徑，N為次流孔數量。

圖1 噴管模型幾何參數Fig.1 The geometrical parameters of nozzle

2.2 內特性參數定義

(1)流量系數

式中：mt為噴管主流實際流量，mc為噴管次流實際流量，mi為噴管理論流量。

(2)推力系數

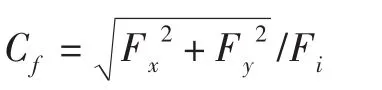
式中：Fx為噴管軸向實際推力，Fy為噴管法向實際推力，Fi為噴管理論推力。

(3)氣動矢量角

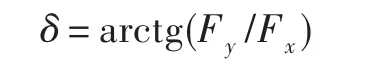
(4)氣動矢量效率

η=δ/[100mc/(mt+mc)]

3 幾何參數對噴管內特性的影響

3.1 次流注入角

對次流注入角α分別為 30°、60°、90°、120°時的雙喉道噴管流場進行模擬，其余幾何結構參數中次流周角固定為60°、空腔擴張角固定為10°、空腔收斂角固定為30°、空腔長度固定為132.68 mm。計算中，噴管主流落壓比取1.89和3.00，前者為雙喉道噴管設計落壓比，后者根據發動機噴管常用落壓比值確定。根據主、次流流量比值范圍，將次流落壓比定為3.10和5.30。矢量特性計算結果見圖2，推力特性和流量特性見圖3。

圖2 氣動矢量角、氣動矢量效率隨次流注入角的變化Fig.2 Vector angle and thrust vector efficiency vs.secondary inject angle

圖3 推力系數、流量系數隨次流注入角的變化Fig.3 Thrust ratio and discharge coefficient vs.secondary inject angle

可見，隨著次流注入角度的增加，兩種主流落壓比(NPRt)下氣動矢量角均呈單調下降趨勢。落壓比為3.00時降幅約5.1°，落壓比為1.89時降幅約5.6°；落壓比為1.89的矢量角總體比落壓比為3.00的高1.0°～1.7°。落壓比為 3.00 時，氣動矢量角最大為11.2°；落壓比為1.89時，氣動矢量角最大為12.9°。這表明次流注入角對噴管氣動矢量角的影響非常明顯，較小的次流注入角有利于次流流量的注入，提升噴管氣動矢量角。隨著次流注入角度的增加，兩種主流落壓比下的氣動矢量效率變化趨勢一致，在前三種次流入射角下，噴管矢量效率變化不大；入射角等于90°后，矢量效率急劇下降，NPRt=3.00/1.89時，矢量效率分別為2.65°/1%和3.33°/1%。這表明入射角90°附近是矢量效率的一個分界點，當次流注入流向與主流流向一致時矢量效率較低，次流注入流向與主流流向相反時能獲得較高的矢量效率。

隨著次流注入角度的增加，兩種主流落壓比下Cf和Cm均呈單邊上升的趨勢，次流的注入改變了噴管流場，進而影響了噴管的Cf和Cm。但不同的次流注入角影響程度不一樣，總體上次流注入角度越大對噴管流場的影響越小，推力損失變越小，Cf和Cm越高。

3.2 次流周向角

對次流周向角β分別為50°、60°、72°、85°時的雙喉道噴管流場進行模擬，結果如圖4～圖7所示。可見，周向角度增加會降低噴管氣動矢量角，較小的次流周向注入角有利于次流流量的注入，提升了噴管的氣動矢量角。落壓比為1.89時周向角為50°的矢量效率最高，達到了4.84°/1%。隨著次流周向角的增大，氣動矢量效率逐漸下降且趨勢變緩，較小的次流周向角有利于提升噴管矢量效率。第一喉道前典型截面的速度云圖基本一致，受次流注入的影響微弱，流場呈現較好的軸對稱性。當次流以不同周向角注入后，在接近次流注入的下游區域，可明顯看出流場的不對稱性。同時，次流周向角越小，次流注入區域越集中，對流場的影響越大，使得噴管矢量角更大、矢量效率更高，流場結果較好地反應了不同周向角下噴管矢量特性的變化結果。

圖4 氣動矢量角、氣動矢量效率隨次流周向角的變化Fig.4 Vector angle and thrust vector efficiency vs.secondary circumferential angle

圖5 周向角50°下噴管典型截面的速度云圖Fig.5 The velocity section contours of 50°circumferential angle

圖6 不同周向角下噴管次流區域下游截面的速度云圖Fig.6 The velocity section contours of different circumferential angles

圖7 推力系數、流量系數隨次流周向角的變化Fig.7 Thrust ratio and discharge coefficient vs.secondary circumferential angle

隨著次流周向角度的增加，兩種主流落壓比下噴管推力系數均呈單邊微弱下降趨勢，且降幅較小，約在0.01以內。次流周向注入角對噴管推力系數的影響微弱。兩種主流落壓比下，除周向角為60°的流量系數較低外，其余流量系數基本一致。

3.3 空腔擴張角

對空腔擴張角θ1分別為 5°、10°、20°時的雙喉道噴管流場進行模擬結果見圖8～圖10。可見，10°空腔擴張角有相對較優的矢量角，空腔擴張角增大到20°時，矢量角及矢量效率劇烈下降，5°和10°的矢量效率基本相當。落壓比為1.89的矢量角和矢量效率均比落壓比3.00的高。

隨著空腔擴張角的增加，噴管推力系數逐漸下降；當落壓比為3.00、空腔擴張角由5°升至20°時，推力系數由0.939降至0.907。由前文可知，擴張角過大不利于噴管矢量偏轉，因此雙喉道氣動矢量噴管的空腔擴張角不宜大于10°。當落壓比為3.00、空腔擴張角由5°升至20°時，流量系數由0.834降至0.780，過大的噴管空腔擴張角不利于噴管流通。

圖8 氣動矢量角、氣動矢量效率隨空腔擴張角的變化Fig.8 Vector angle and thrust vector efficiency vs.cavity divergence angle

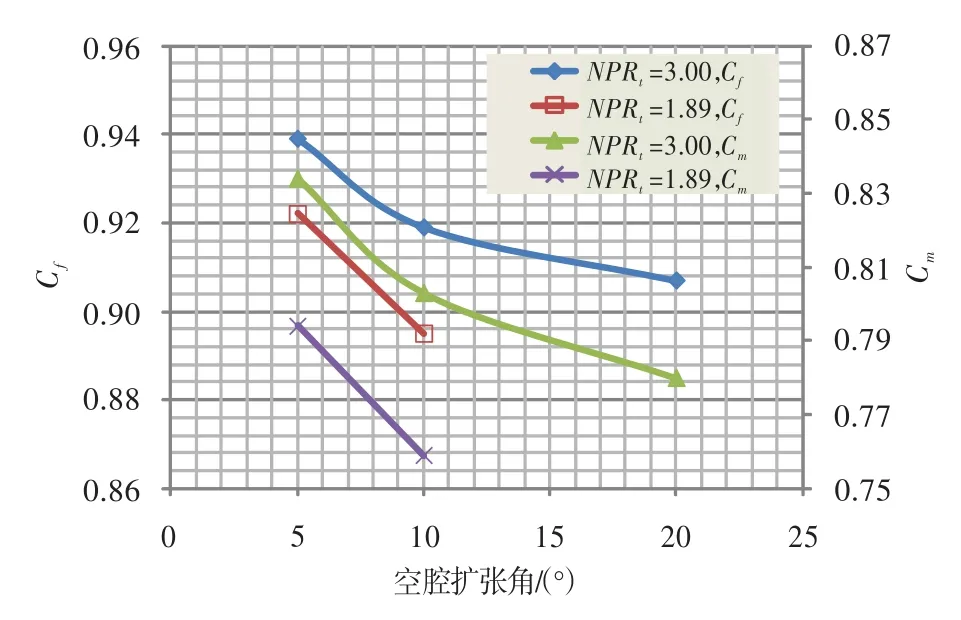
圖9 推力系數、流量系數隨空腔擴張角的變化Fig.9 Thrust ratio and discharge coefficient vs.cavity divergence angle

圖10 不同擴張角下噴管的三維流線圖Fig.10 The 3D streamline pattern of different cavity divergence angles

從不同擴張角下噴管的三維流線圖中可看出，在空腔頂部形成了回流區，5°的回流區比10°的明顯偏小，因而10°的矢量偏轉角較5°的大。20°擴張角中，在空腔上下形成了兩個回流區，其相互作用導致該結構矢量角偏小，同時使噴管流動損失增大，導致其流量系數、推力系數降低。

3.4 空腔收斂角

由圖11可以看出，噴管氣動矢量角隨空腔收斂角θ2的變化幅度非常明顯，兩種落壓比下矢量角均單調上升；設計落壓比下，空腔收斂角由10°變化至40°時，矢量角由6.3°增至13.8°。矢量效率增幅也非常顯著，空腔收斂角由10°變化至40°時，矢量效率由2.58°/1%增至4.59°/1%，且增幅主要出現在收斂角由 10°增至 30°的過程中；30°與 40°的矢量效率基本相當。

圖11 氣動矢量角、氣動矢量效率隨空腔收斂角的變化Fig.11 Vector angle and thrust vector efficiency vs.cavity convergence angle

圖12 推力系數、流量系數隨空腔收斂角的變化Fig.12 Thrust ratio and discharge coefficient vs.cavity convergence angle

從圖12中可以看出，隨著空腔收斂角的增加，噴管推力系數有下降趨勢但不明顯，噴管流量系數逐漸下降；當落壓比為1.89、空腔收斂角由20°升至40°時，流量系數由0.801降至0.727。因此，過大的噴管空腔收斂角不利于噴管流通。

從流線對比圖(圖13)中可看出，空腔上部回流區的大小和回流區周邊低速高壓氣流的方向。收斂角從10°增至40°的過程中，回流區逐漸加大，壓迫主流的能力增強，同時回流區周邊低速高壓氣流的方向逐漸由平行噴管出口方向到上偏，使得主流矢量偏轉角明顯增大。這是由于收斂角變化引起空腔結構變化和收斂角的導流作用所致。

3.5 空腔長度

圖13 不同收斂角下噴管的三維流線圖Fig.13 The 3D streamline pattern of different cavity convergence angle

圖14 氣動矢量角、氣動矢量效率隨空腔長度的變化Fig.14 Vector angle and thrust vector efficiency vs.cavity length

由圖14可以看出，噴管氣動矢量角隨空腔長度的變化幅度非常明顯，兩種落壓比下矢量角均呈現單調上升趨勢。設計落壓比下，空腔長度由107.00 mm變化至184.10 mm時，矢量角由10.5°增加至14.8°。矢量效率的增幅也非常顯著，設計落壓比下，空腔長度由107.00 mm變化至184.10 mm時，矢量效率由4.03°/1%增加至5.35°/1%，且增幅主要出現在空腔長度由107.00 mm增加至158.40 mm的過程中，158.40 mm與184.10 mm的矢量效率基本相當。落壓比為3.00時，氣動矢量角呈線性增加，從9.2°增加到14.2°，增幅明顯；矢量效率也幾乎呈線性增加。以上表明，空腔較長有利于噴管矢量角增加。

圖15中，隨著空腔長度的增加，落壓比為3.00時，噴管推力系數在0.92～0.93之間波動。設計落壓比下，前三種噴管空腔長度中，推力系數在0.90附近波動，噴管長度對噴管推力系數的影響微弱。噴管流量系數呈單調下降趨勢，設計落壓比時下降了0.042，落壓比為3.00時下降了0.030。空腔長度增加，空腔最大直徑相應增加，導致流阻加大，流量系數下降。

圖15 推力系數、流量系數隨空腔長度的變化Fig.15 Thrust ratio and discharge coefficient vs.cavity length

由圖16的流線對比圖可看出空腔不同長度時上部回流區的大小和長度。隨著空腔長度的增加，形成回流區的空間不斷增加，壓迫主流的能力增強，使得主流矢量偏轉的角度也相應增加。圖17給出了空腔長度分別為107.00 mm和184.10 mm的噴管上下壁面區域壓力分布曲線，可見后者的上下區域壁面壓差明顯比前者大，較大的壓差有利于促進噴管氣流矢量角的產生。

圖16 不同空腔長度下噴管的三維流線圖Fig.16 The 3D streamline pattern of different cavity length

圖17 不同空腔長度下噴管上下壁面區域的壓力分布Fig.17 Wall pressures distribution of different cavity length

4 幾何參數優選

綜合前文的影響結果，優化出了一組雙喉道氣動矢量噴管的幾何參數，見表1；優化前后的內特性計算結果見表2，表中NPRc為次流落壓比。

表1 優選的噴管幾何參數Table 1 The optimized geometrical parameters of nozzle

表2 優化前后噴管內特性計算結果及對比Table 2 The comparison of nozzle internal performance before and after optimization

由表2可知，優化后設計點噴管矢量角較落壓比為3.00的工況高。15.5°的矢量角基本可滿足目前飛機對噴管矢量角的要求，且引氣量較少；設計落壓比及落壓比為3.00的工況下，次流引氣流量約為2.8%時推力特性(0.920、0.932)較好，氣動矢量效率也大于5.00°/1%，遠高于激波誘導式氣動矢量噴管的氣動矢量效率(1.70°/1%)[5]。適當減小次流入射角、次流周向角，增長噴管長度等對噴管進行了優化。上述參數的變化對噴管流量特性有一定的不利影響，噴管流量系數相比優化前降低了1%～2%。優化后的幾何參數對噴管推力特性產生了積極影響，落壓比為3.00時的計算工況下，推力系數達到了0.932，高于激波誘導式及其它喉道偏移式氣動矢量噴管的推力系數(0.900左右[5])。

5 結論

本文對軸對稱雙喉道氣動矢量噴管主要幾何參數對噴管內特性的影響進行了計算分析，結果表明：次流注入角、空腔收斂角、空腔長度等幾何因素對噴管矢量特性影響較大，次流注入角、空腔擴張角等對噴管推力特性有較大影響。空腔上部回流區大小直接影響到噴管矢量性能，擴張角為20°時，空腔上、下部出現了雙回流區，使矢量特性下降。根據分析結果，對噴管幾何參數進行優化，得到了一組相對較優的雙喉道氣動矢量噴管幾何參數，優化后的噴管矢量角可達到15.5°，矢量效率達5.70°/1%，噴管推力系數為0.920。

[1]Deere K A，Berrier B L，Flamm J D.Computational Study of Fluidic Thrust Vectoring Using Separation Control in a Nozzle[R].AIAA 2003-3803，2003.

[2]Flamm J D，Deere K A，Berrier B L，et al.An Experimen?tal Study of a Dual Throat Fluidic Thrust Vectoring Nozzle Concept[R].AIAA 2005-3503，2005.

[3]周慧晨，譚慧俊，孫 姝，等.一種矢量增強型雙喉道射流推力矢量噴管的數值模擬[J].航空動力學報，2010，25(9)：2070—2076.

[4]卿太木，廖華琳，朱 川.軸對稱雙喉道流體控制矢量噴管三維數值模擬[J].燃氣渦輪試驗與研究2009，22(3)：14—18.

[5]張群鋒.軸對稱射流矢量噴管的試驗和數值模擬[J].推進技術，2004，25(2)：139—143.