DTB型結晶器高徑比對流場影響的研究

付存然，沙作良，朱 亮，李福濤

(天津市海洋資源與化學重點實驗室，天津市海洋化工與技術工程中心，天津科技大學海洋科學與工程學院，天津 300457)

DTB(draft tube baffle)型結晶器是 20 世紀 50 年代末出現的一種效能較高的結晶器．目前，在美國、日本等國，DTB型結晶器為連續結晶器的主要型式之一，可用于真空冷卻法、蒸發法、直接接觸冷凍法及反應法的結晶過程[1]．但長期以來，人們對于 DTB型結晶器結晶過程的研究主要集中在結晶動力學數據方面，很少有人研究液相流場和固相懸浮狀態對結晶過程的影響，這主要是由于結晶器內多相流體系的非線性、結晶的不均勻性和流域的多態性[2]很難通過實驗室模型獲得液相流場信息和懸浮密度分布．而晶體的成長速率很大程度依賴于結晶器內的液相流場[3]；Sha等[4]的研究證明，固相懸浮狀態對結晶過程也有很大的影響．因此，為能更加清楚地了解結晶過程，考察結晶器內的液相流場和固相懸浮狀態十分必要．

計算流體力學(CFD)以計算機為工具，通過對流體運動方程的數值解法研究流體在不同過程中的流動狀態及其對流動過程中所發生的傳質、傳熱等過程的影響，對多相流場進行模擬，并通過現代的作圖手段把過程的進程展現為可見過程，實現仿真模擬．所以，將 CFD應用于化學工程的模擬中有很高的理論價值和廣泛的應用價值[5]，可以作為研究結晶過程中液相流場和固相懸浮狀態的有力工具[6–7]．

文中采用CFD商業軟件ANSYS，對同一結構不同高度的 DTB型結晶器進行模擬，通過對液相流場、固相懸浮狀態以及結晶器內不同區域中平均懸浮密度分布規律的研究，考察結晶器高度對結晶器內流體動力學和晶體分布的影響，為結晶器的設計和優化提供理論依據．

1 模 型

實驗使用歐拉–歐拉法，對一個液相和 5個不同尺寸的固相顆粒的多相流體系進行模擬．該方法將液相和各固相均認為連續作用的相，各相之間發生相互作用．根據歐拉-歐拉方程，多相流場中任意一相質量平衡的連續性方程為

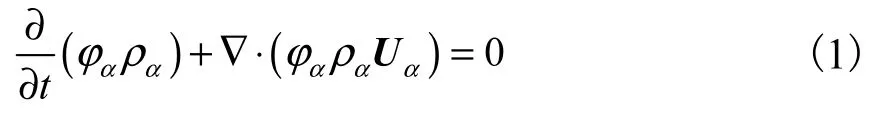
式中：下標 α＝β、γ、…，分別表示連續相和各分散相；φα為第 α相的相含率，為密度，kg/m3；Uα是速度矢量，m/s；t為時間，s；?為散度．

描述流動速度的分布，可通過動量守恒定律來計算，方程為

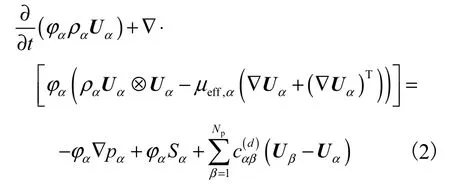
式中：μeff，α(α?U＋(α?U)Τ)表示流體受到的剪應力；pα表示壓力，Pa；Sα為將傳遞方程寫為通用形式而產生的源相；NP為相的個數；d為顆粒直徑，m；為流體所受外力提供的動量，此外力除攪拌槳提供的運動能量之外，主要指連續相與分散相間的各種相互作用力，包括湍流阻力、曳力和形體阻力等．為了簡化模擬，僅考慮起主要作用的曳力，相間曳力系數由式(3)估算．

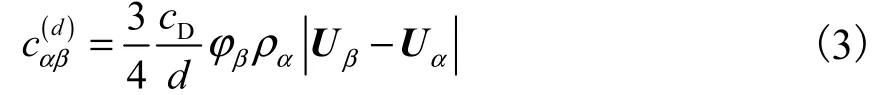
系數cD可有多種模型，本研究中使用Schiller等的模型[8]

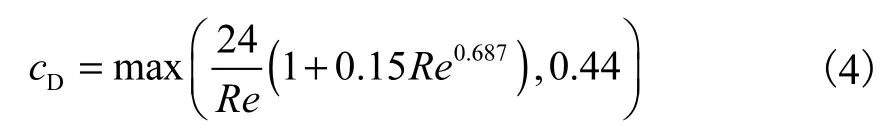
式(4)中雷諾數Re被定義為

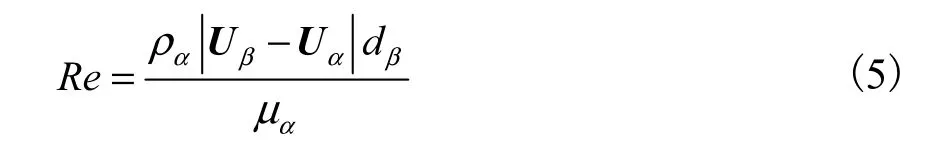
工業結晶器內的流動狀態一般是在湍流下進行，流體的湍流特征可用 k–ε、k–ω 模型，以及雷諾剪應力等湍流模型進行描述．一般認為標準 k–ε模型[9]可以滿足工程流場計算的要求．根據標準 k–ε模型，式(2)中的渦流黏度項可表示為

式中：μα為動力學黏度，Pa·s；μT,α為湍流黏度，Pa·s．

式中：Cμ為常數；κα為湍動能，m2/s2；εα為湍動能耗散，m2/s3．

2 模 擬

結晶器的底部呈 W 型結構，內部設 4個擋板，進、出口均位于導流筒外部．攪拌槳由 4個傾斜角為60°的長方形平直槳葉組成．結晶器結構如圖 1所示，具體尺寸見表 1．結晶器Ⅰ和結晶器Ⅱ的主要區別是結晶器的高度不一樣，因為高度的不同，導致進出口長度的不同，其他條件是一致的．

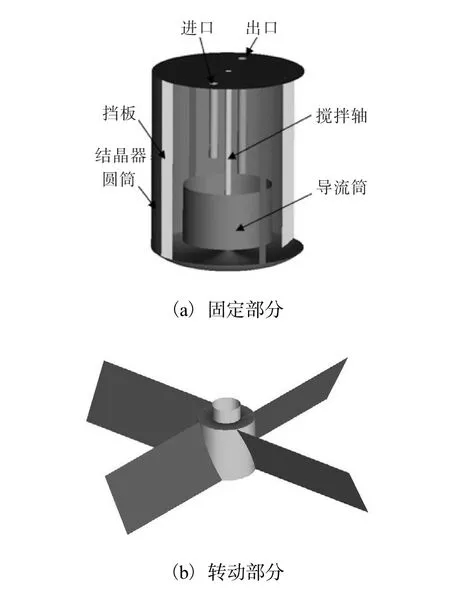
圖1 DTB型結晶器的固定部分和轉動部分的結構圖Fig.1 The construction of the fixed part and the rotating part of DTB crystallizer

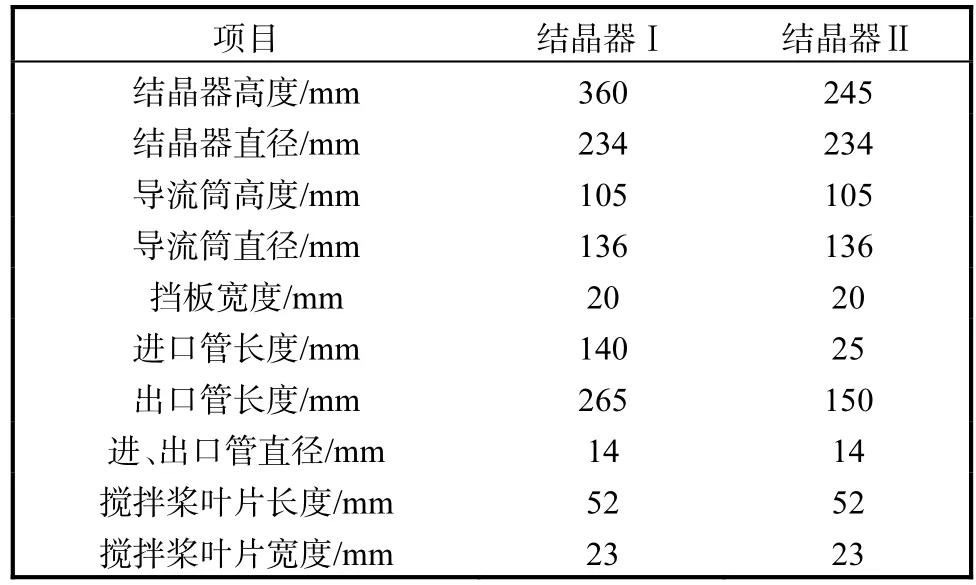
表1 DTB型結晶器的主要尺寸Tab.1 The main size of the DTB crystallizer

為研究結晶器內不同區域中平均懸浮密度的分布規律，模擬前需對結晶器進行合理分區．區域大小的選擇是一個關鍵，如果區域太大，此區域中晶體沒有達到完全懸浮；而區域過小時，此區域的結晶行為與鄰近區域類似，造成計算浪費．通過對懸浮狀態模擬結果的分析，可將結晶器分為大小不等的環狀區域．用距軸心分別為 68、97,mm 的曲面，和距結晶器底部分別為 40、70、145、245,mm 的水平面將結晶器Ⅰ分為 15個環狀區域；同理，用距軸心分別為 68、97,mm 的曲面，和距結晶器底部分別為 40、70、145,mm的水平面將結晶器Ⅱ分為 12個環狀區域，如圖2所示．

圖2 結晶器分區示意圖Fig.2 The schematic diagram of the zoning of the crystallizer

基于多相流的連續介質模型，將固相視為擬流體，液相設視為連續相[9]．固相密度為 1,984,kg/m3，黏度近似為 0；液相密度為 997,kg/m3，黏度為8.899×10-4,Pa·s．在一般結晶過程中，不同粒度的晶體在結晶器中的分布呈近似的正態分布[9]，因此對于目標粒度為0.5,mm的冷卻連續結晶過程的模擬可以依據正態分布進行假設，模擬中使用5個特征尺寸的固相作為不同的分散相，設定結晶器中考慮的晶體的尺寸范圍為 0.1～1.0,mm，在這范圍之中粒度為 0.1、0.3、0.5、0.7、1.0,mm 的固相的體積分數分別為 1%、2%、4%、2%、1%．

模擬基本參數的設定如下：攪拌槳攪拌速度400,r/min；進口固液體系流速 0.3,m/s；進口固相的體積分數 10%；進口液相的體積分數 90%；出口壓力恒定，相對大氣壓力為0．

3 結果與討論

3.1 不同高徑比的DTB結晶器液相流場的特征

結晶器Ⅰ的液相流場分布如圖 3所示．由圖 3可以看出：在導流筒附近明顯存在著流體循環．在導流筒內，靠近導流筒壁的小部分流體向上升，靠近攪拌槳軸的大部分流體向下降；而導流筒外，流體的整體趨勢是向上的．在導流筒內，緊貼內壁區域的流體速度明顯大于周圍的流體速度．

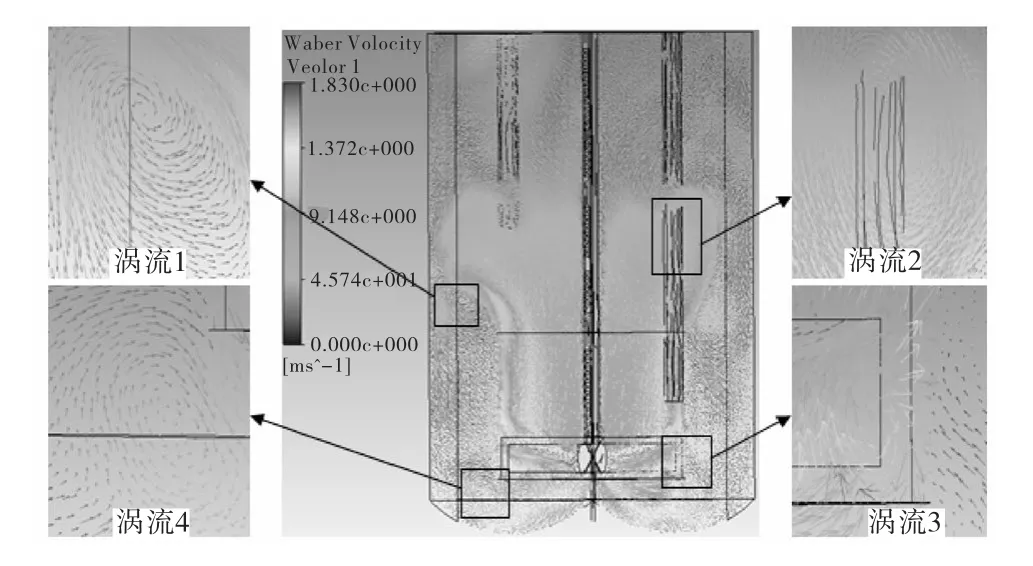
圖3 結晶器Ⅰ的液相流場分布圖Fig.3 The liquid flow field distribution of crystallizer Ⅰ

在液相流場中出現了大小不同的漩渦，幾個比較明顯的漩渦見圖 3中的放大圖．在導流筒與結晶器壁面形成的環隙區域，且靠近導流筒入口處的低速流體，由于受到了從導流筒上端噴射出的高速流體的影響，形成了邊界層分離，因此形成了漩渦1；在導流筒上方，由于速度較大的流體突然擺脫了導流筒的束縛，受攪拌槳的離心作用減弱，重力作用增強，從而流動方向發生改變，形成了漩渦 2；在攪拌槳尖端附近，由于很強的離心作用，流體流速很大，流體一部分與攪拌槳和導流筒空隙間的低速流體相遇，形成了漩渦 3；另一部分則從導流筒的下端被甩出，在結晶器底部，形成了漩渦4．

結晶器Ⅱ的液相流場分布如圖4所示．對比圖3與圖4可以看出：結晶器Ⅰ比結晶器Ⅱ頂部多出來的液相流場，流速明顯較低；兩個結晶器內漩渦的大小和位置稍有差異，相對于結晶器Ⅰ，結晶器Ⅱ中的漩渦1比較弱，而漩渦4比較強，且漩渦4更偏向結晶器壁面．

圖4 結晶器Ⅱ的液相流場分布圖Fig.4 The liquid flow field distribution of crystallizer Ⅱ

3.2 不同高徑比的 DTB結晶器中不同粒度的固相

懸浮狀態的比較

圖5為結晶器Ⅰ(左圖)和結晶器Ⅱ(右圖)中，不同粒度晶體混合模擬后得到的不同粒度的固相體積分數的分布圖．由圖 5可以看出：(1)固體顆粒由于受到液相流場的影響，在結晶器內呈現出固相整體分布不均勻的特征；由于受到漩渦的影響，漩渦中心的液固相因離心力的作用，大部分被甩向漩渦邊緣，形成局部固相低濃區域，而漩渦邊緣部分液體的流速相對較低，固相在這里富集，形成局部固相高濃區域．(2)同一結晶器中，固相粒度越小，分布越均勻；相反，固相粒度越大，分布越不均勻．在相同的流場下，不同粒度的固體顆粒，會呈現出不同的懸浮狀態，因此在一定的操作條件下，結晶器內不同位置會形成不同粒度分布的晶體產品．(3)結晶器的高徑比越大，結晶器上部出現的細晶越多，而且軸向上大顆粒固相的體積分數的波動性越大，晶體產品的粒度分布對出料口位置越敏感．

圖5 結晶器Ⅰ(左圖)和結晶器Ⅱ(右圖)中不同粒度的固相體積分數分布圖Fig.5 The crystal volume fraction distribution of particles of different size in crystallizerⅠ(left) and crystallizerⅡ(right)

3.3 不同高徑比的 DTB結晶器中固相的平均體積分數沿軸向和徑向分布的比較

將結晶器Ⅰ、Ⅱ中，到軸心距離相同，而到結晶器底部距離不同的區域固相平均體積分數的分布繪制成折線圖，如圖6所示．

從圖 6可以看出：(1)在結晶器Ⅰ和結晶器Ⅱ中，到軸心距離分別為97,mm和117,mm的區域，固相顆粒體積分數隨著高度的增加而逐漸減小，而到軸心距離為68,mm，到底部距離為70,mm的區域，因受攪拌槳離心力的影響，固相體積分數很低．(2)在結晶器Ⅰ中，距離軸心為68,mm的區域底部，固相顆粒體積分數最高；而在結晶器Ⅱ中，距離軸心為117,mm 的區域底部，固相顆粒體積分數最高，這主要是由結晶器Ⅰ、Ⅱ底部兩個漩渦位置差異導致的；除結晶器底部外，結晶器Ⅰ、Ⅱ中其他區域越靠近結晶器壁面，固相體積分數越高．(3)結晶器的高徑比越大，沉積在結晶器底部的顆粒越多，而懸浮在結晶器頂部的顆粒越少，懸浮密度的均勻程度就越差，從而影響晶體的成核和生長過程，不利于得到粒度分布均勻的晶體產品．

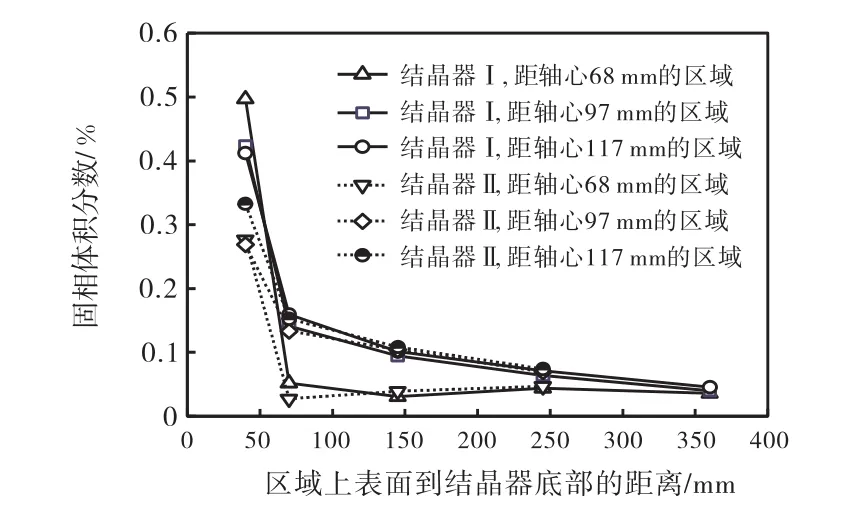
圖6 不同高徑比的 DTB結晶器徑向距離相同而軸向高度不同的區域中固相平均體積分數的分布Fig.6 The local area volume fraction distribution of identical radial distance and different axial height in a crystallizer with different ratios of height to diameter

4 結 論

通過對相同操作條件下同一結構不同高徑比的DTB型結晶器中流場的模擬可知：高徑比對結晶器內液相流場的循環有很大影響，進而使得固相體積分數的分布也有很大差異；高徑比越大，各粒度的固相沿軸向的分布越不均勻，因而晶體產品的粒度分布對出料口的位置越敏感；高徑比越大，晶體的懸浮狀態越不理想，對結晶過程越不利，影響晶體產品粒度分布的均勻性．所以，結晶器的高度是晶體粒度控制的影響因素之一，在結晶器的設計與優化中應予考慮．

［1］ 謝東宏. DTB 型結晶器[J]. 化工機械，1994，21(1)：55–57.

［2］ Simanovskii I B，Viviani A，Legros J C. Nonlinear convective flows in multilayer fluid system[J]. European Journal of Mechanics-B/Fluids，2008，27(5)：632–641.

［3］ Liu C R，Huhe A D，Ma W J. Numerical and experimental investigation of flow over a semicircular weir[J].Acta Mechanica Sinica，2002，18(6)：594–602.

［4］ Sha Z L，Palosaari S. Modeling and simulation of crystal size distribution in imperfectly mixed suspension crystallization[J]. Journal of Chemical Engineering of Japan，2002，35(11)：1188–1195.

［5］ 黃永春，唐軍，謝清若，等. 計算流體力學在化學工程中的應用[J]. 現代化工，2007，27(5)：65–68.

［6］ Vakili M H，Esfahany M N. CFD analysis of turbulence in a baffled stirred tank，a three-compartment model[J].Chemical Engineering Science，2009，64(2)：351–362.

［7］ Wadnerkar D，Utikar R P，Tade M O，et al. CFD simulation of solid–liquid stirred tanks[J]. Advanced Powder Technology，2012，23(4)：445–453.

［8］ Schiller L，Naumann A. Fundamental calculations in gravitational processing[J]. Zeitschrift des Vereines Deutscher Ingenieure，1933，77：318–320.

［9］ 李靜海. 顆粒流體復雜系統的多尺度模擬[M]. 北京：科學出版社，2005：37–40.