關于四類函數的幾個結論

楊明順

(渭南師范學院數學與信息科學學院,陜西渭南 714099)

關于四類函數的幾個結論

楊明順

(渭南師范學院數學與信息科學學院,陜西渭南 714099)

利用初等及組合方法對連續函數、單調函數、有界變差函數、絕對連續函數的關系進行了探討,得出了絕對連續函數一定是有界變差函數,單調函數是有界變差函數,絕對連續函數一定是連續函數的結論.

連續函數;單調函數;有界變差函數;絕對連續函數

連續函數、單調函數、有界變差函數、絕對連續函數是函數論中廣泛使用的四類函數,搞清楚它們之間的關系對于掌握這些函數很有必要.目前有關研究它們之間關系的完整結果很少看到,本文就此問題進行了探究.

定義1[1]設f(x)是定義在點集E?R上的函數,x0∈E,若對?ε＞0,?δ＞0,當x∈E∩U(x0, δ)時,有f(x)-f(x0)＜ε,則稱f(x)在x0上連續,如果f(x)在E上每點都連續,就稱f(x)在E上連續.

定義2[1]設f(x)是定義在實直線R中點集E上的有限函數,如果對任意x1,x2∈E,當x1＜x2時,不等式f(x1)≤f(x2)恒成立,就稱f(x)是E上的單調增加函數,如果不等式f(x1)＜f(x2)恒成立,就稱f(x)是E上的嚴格單調增加函數;如果當x1＜x2時,不等式f(x1)≥f(x2)恒成立,就稱f(x)是E上的單調減少函數,如果不等式f(x1)＞f(x2)恒成立,就稱f(x)是E上的嚴格單調減少函數.

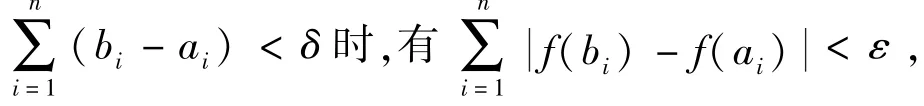
1.絕對連續函數一定是有界變差函數

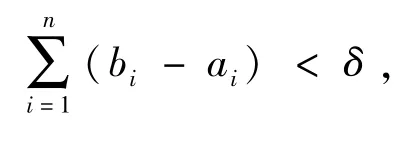
2.單調函數是有界變差函數

3.絕對連續函數一定是連續函數

4.連續函數不一定是有界變差函數

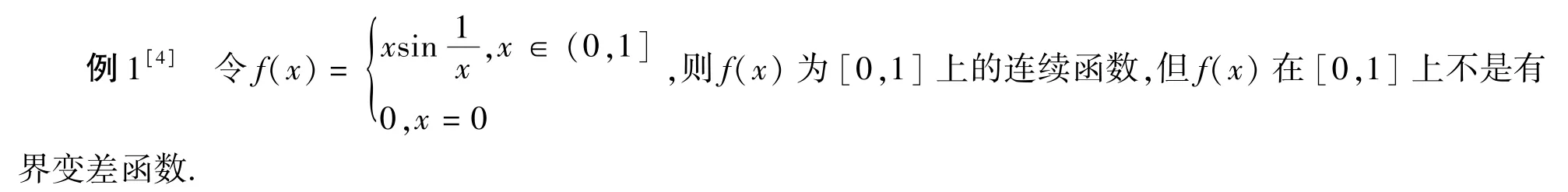
5.有界變差函數不一定是連續函數

6.有界變差函數不一定是絕對連續函數

7.有界變差函數不一定是單調函數

例4 設f(x)=x,g(x)=x2,在[0,1]上都單調增加,令:H(x)=f(x)-g(x),x∈[0,1],則H(x)在[0,1]上有界變差函數,但H(x)在[0,1]上不是單調函數.

8.絕對連續函數不一定是單調函數

絕對連續函數一定是有界變差函數,而有界變差函數不一定是單調函數,從而可知:絕對連續函數不一定是單調函數.

9.單調函數不一定是絕對連續函數

10.單調函數不一定是連續函數

11.連續函數不一定是單調函數

例7 設f(x)=x2,則f(x)在定義域(-∞,+∞)內是連續的,但不是單調函數.

12.連續函數不一定是絕對連續函數

[1]趙靜輝,徐吉華.實變函數簡明教程(函數論部分)[M].武漢:華中科技大學出版社,1996.86-96.

[2]胡適耕.實變函數(微分論部分)[M].北京:高等教育出版社,1997.153-160.

[3]張曉嵐.實變函數與泛函分析簡明教程[M].北京:高等教育出版社,2000.65-75.

[4]張喜堂.實變函數論的典型問題與方法[M].武漢:華中師范大學出版社,2000.307-320.

[5]胡長松.實變函數(有界變差函數)[M].北京:科學出版社,2002.133-134.

【責任編輯 牛懷崗】

On Several Conclusions about Four Kinds of Functions

YANG Ming-shun
(School of Mathematics and Information Science,Weinan Normal University,Weinan 714099,China)

The paper,based on the elementary function and the combinatorialmethod,discussed the relation between the continuous function,themonotonic function,the bounded variation function and the definitely continuous function.It proved that the absolute continuous functionmust be the bounded variation function,monotone function is a function of bounded variation,and absolutely continuous function is a continuous function.

continuous function;monotonic function;bounded variation function;definitely continuous function

O156.4

A

1009-5128(2014)03-0016-03

2013-09-30

陜西省教育廳科學研究計劃(自然科學專項)項目:關于F.Smarandache數論問題的計算機輔助研究(2013JK1165);渭南師范學院教改項目:大學數學教學改革的探索與實踐(JG201345)

楊明順(1964—),男,陜西渭南人,渭南師范學院數學與信息科學學院教授,主要從事數論研究.