非高斯雜波下知識輔助檢測器敏感性分析

鄒 鯤 廖桂生 李 軍 李 偉 李天星

?

非高斯雜波下知識輔助檢測器敏感性分析

鄒 鯤*①②廖桂生①李 軍①李 偉②李天星③

①(西安電子科技大學雷達信號處理國家重點實驗室 西安 710071)②(空軍工程大學信息與導航學院 西安 710077)③(國家知識產權局專利局專利審查協作中心 北京 100190)

先驗信息的使用可以提高知識輔助檢測器的探測性能，若先驗信息與當前探測環境不匹配，檢測器性能可能會受到影響。該文考慮一種復合高斯雜波下的知識輔助檢測器，其采用逆伽馬分布作為紋理分量先驗分布，分析該檢測器在不同雜波紋理分量模型參數條件下的檢測性能。首先給出了先驗模型參數失配條件下，虛警概率和Swerling I型目標檢測概率的計算方法。然后在給定先驗模型參數條件下，分析了雜波紋理分量分布參數對檢測器性能的影響。理論分析表明，若雜波紋理分量分布參數位于某個區域以內時，檢測器可以獲得比模型匹配時更好的檢測性能，計算機仿真驗證了上述結論。

雷達信號處理；知識輔助檢測器；復合高斯；逆伽馬分布；先驗模型失配

1 引言

復雜電磁環境中感興趣目標的探測是雷達的主要任務之一，而目標的探測能力與雜波統計特性密切相關。在信號檢測器設計階段，需要確定雜波統計分布，必要時還需要對雜波統計分布參數進行估計。基于高斯分布的雜波統計模型的信號檢測問題已經獲得了廣泛的研究。但隨著雷達分辨率的提高，單個分辨單元內的獨立散射點的個數減少，后向散射回波的起伏特性不滿足中心極限定律，雜波的統計往往表現為非高斯性[1]。在所有非高斯分布模型中，復合高斯分布模型獲得了深入的研究[2]。一方面是因為復合高斯分布是一種局部化高斯分布模型，是橢圓對稱分布的特例[3]，在理論分析上可以借鑒基于高斯分布的研究成果。另一方面是因為復合高斯分布可以擬合大多數非高斯分布模型，如K分布，Welbull分布等，并在實測數據統計分析中獲得了驗證。

目前針對逆伽馬分布紋理的知識輔助檢測器研究較多，如鄒鯤等人[11,12]討論了點目標的知識輔助檢測，并應用于實測數據取得了較好的效果，Bandiera等人[13,14]研究了協方差矩陣估計問題和分布目標的知識輔助檢測問題，尚秀芹等人[15]研究了不同檢測策略下的知識輔助檢測器，Balleri等人[16]研究了逆伽馬分布紋理參數的估計問題，Sangston等人[17]研究了檢測器的動態門限的計算問題。這些研究結果表明，利用雜波紋理分量的先驗信息，有助于提高檢測器在非高斯雜波中的探測性能，但現有文獻對先驗信息失配條件下的檢測性能研究較少，且缺少定量分析結論。

先驗信息的獲取一般來自對歷史環境的統計分析，是雷達對探測環境的記憶。然而由于雷達系統本身的不穩定性，探測環境的空時域變化，先驗信息獲取過程的不確定性等因素，先驗信息模型與當前探測環境之間可能不匹配。當這種失配程度較小時，檢測器的性能受到的影響可忽略；但當這種失配足夠大時，先驗信息不能為當前探測環境提供合理的輔助信息，甚至會給出錯誤的信息，此時的知識輔助的檢測器性能可能比不使用先驗信息的檢測器的性能更差。因此針對知識輔助檢測器的敏感性問題，即分析該檢測器在不同的探測環境下的檢測性能是有必要的。

本文第2節推導了逆伽馬分布紋理的復合高斯雜波下的知識輔助檢測器，第3節給出了知識輔助檢測器在先驗信息失配時的檢測性能的計算公式，第4節分析了知識輔助檢測器在先驗模型失配時的敏感性，最后給出了全文的結論。

2 復合高斯雜波下的知識輔助檢測器

雷達目標的檢測問題屬于統計假設二元檢驗，假定雷達陣列天線將接收到的回波信號進行下變頻、AD采樣、正交解調、多脈沖累積后，可以得到空時聯合域的待檢測數據是維矢量，即=ea，其中e是天線陣元的個數，a是脈沖累積個數。維復合高斯分布矢量可以表示為式(1)所示的兩個獨立分量的乘積。

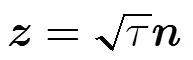
其中維矢量稱為散斑分量，其滿足零均值，正定Hermitian協方差矩陣的復高斯分布，即~CN(0,)。本文假定已知或可以通過估計得到。標量為非負的隨機變量，稱為紋理分量，其概率密度函數為。由此可以得到式(2)所示的復合高斯分布矢量的概率密度函數。

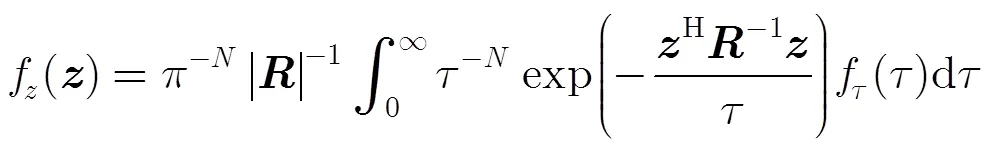
本文假定紋理分量滿足式(3)所示的逆伽馬分布：

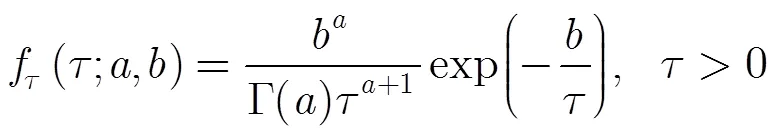
逆伽馬分布為雙參數分布，包含有形狀參數和尺度參數。將式(3)代入式(2)可以得

可見，當紋理分量為逆伽馬分布時，矢量滿足自由度為的復分布[18]。由此可以得到似然比檢驗[11]：

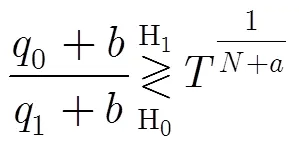
其中

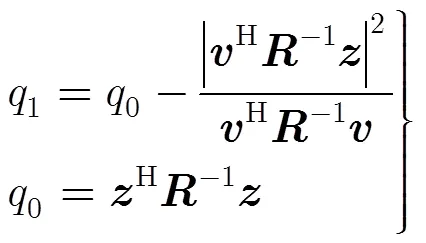
式中維矢量為目標導向矢量，并假定已知，為檢測門限，與指定的虛警率有關。

3 先驗模型失配條件下的知識輔助檢測器性能分析

3.1 虛警率的計算

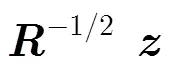
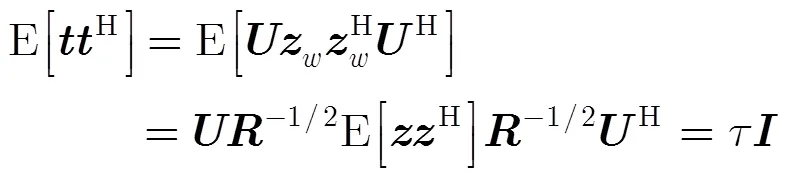
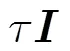
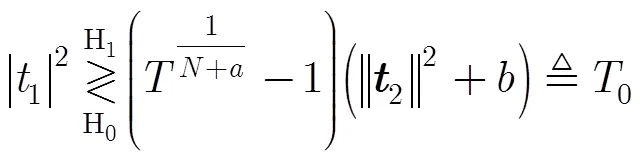
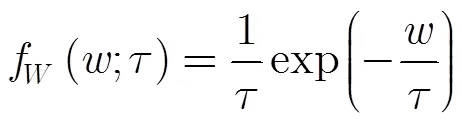
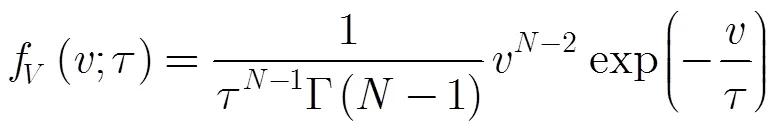
利用上述結論，可以得到條件虛警率：

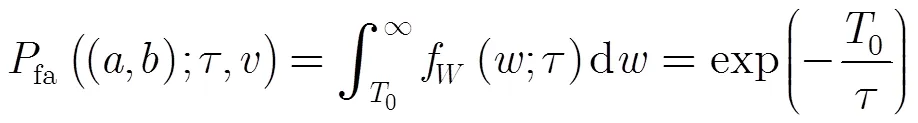
其中門限0的定義見式(8)，與參數(,)有關。考慮先驗模型失配時的虛警率，即假定實際雜波紋理分布參數為(,)，利用式(3)和式(10)推導可以得到

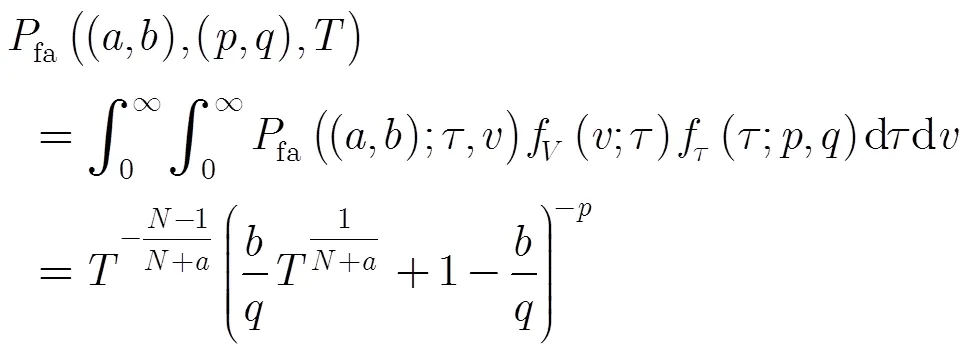
如果假定=,=，即先驗模型不存在失配，則先驗模型匹配時的虛警率[17]為

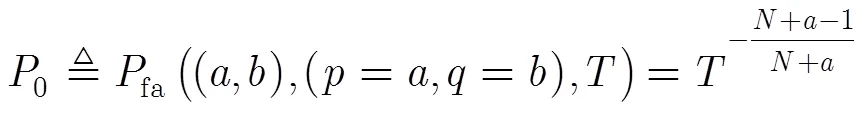
在檢測器設計階段，通常指定0，由式(13)得到門限。利用門限和虛警率的關系，式(12)可以得到

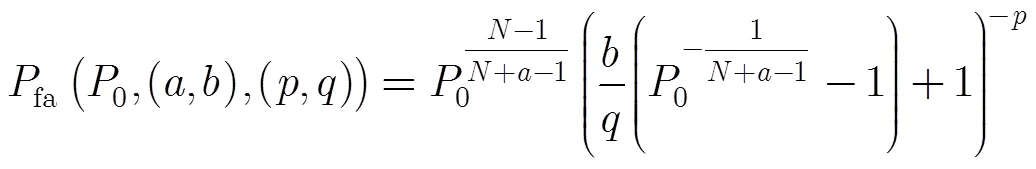
可見，在先驗模型失配條件下，檢測器的虛警率除了與設定的虛警率標稱值0有關，還與先驗模型參數(,)和雜波場景模型參數(,)有關。

3.2 檢測概率的計算

檢測概率與目標類型有關，考慮到計算復雜性，本文選擇Swerling I型目標計算檢測概率。變量的概率密度函數為

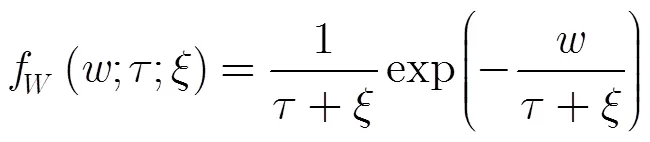
其中信雜比(Signal Clutter Ratio, SCR)定義為SCR。由此可以得到條件檢測概率為

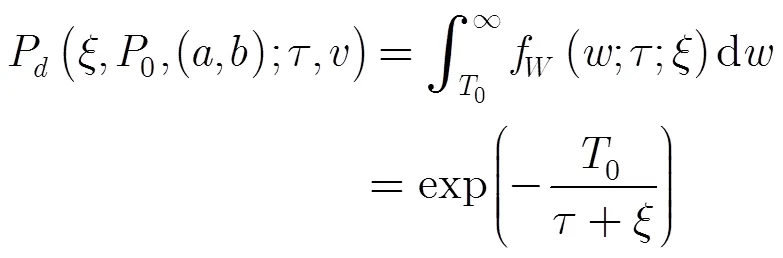
設雜波紋理分量參數為(,)，則檢測概率為

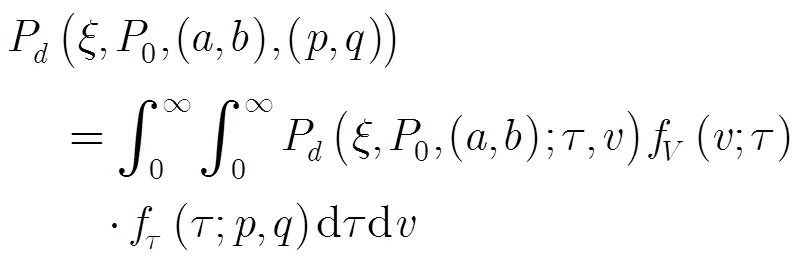
利用式(10)和式(3)，經過推導可得

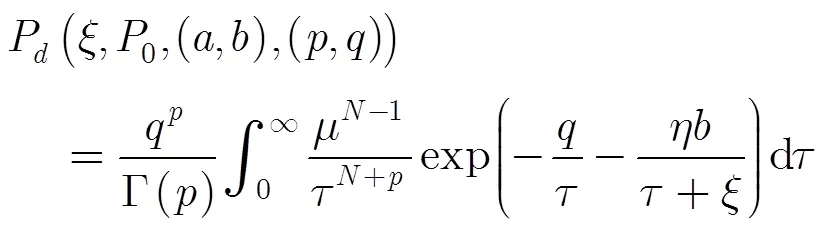
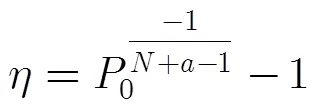
需要指出的是，只有采用Swerling I類型目標才可以獲得較為簡單的檢測概率計算公式。利用式(18)可以得到先驗模型與探測環境匹配時的檢測概率為

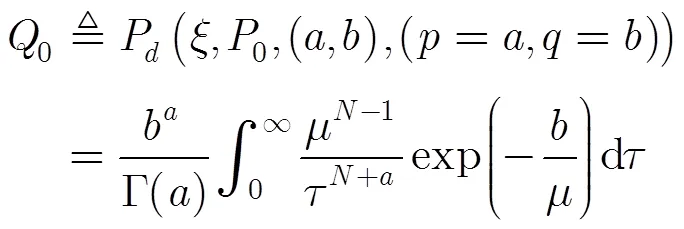
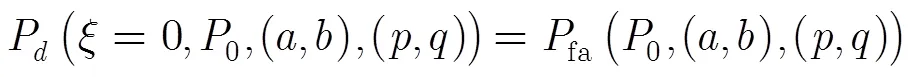
4 知識輔助檢測器敏感性分析

知識輔助檢測器，如式(5)所示，檢測器結構和判決門限中包含了先驗信息模型參數(,)。檢測器的敏感性分析則是討論該檢測器在模型參數(,)的雜波場景中探測性能。由上述分析結果可知，不同的參數(,)會導致檢測器的檢測性能存在差異。利用式(14)和式(18)可以得到(,)的兩個約束關系為

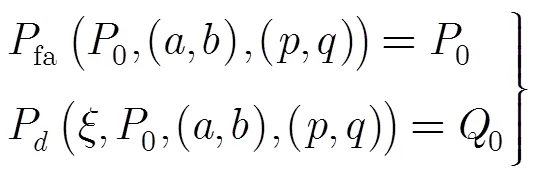
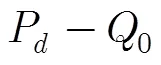
圖3給出了==2時的檢測器敏感性的計算機仿真結果，所得到的結論與前面類似，也存在一個穩健區間，位于兩個約束關系的左上方。利用逆伽馬概率密度函數以及復合高斯雜波模型的特點[11]可知，對于(,)平面左上方，值較小，而值較大，表明雜波環境的非高斯性較弱。對于知識輔助檢測器式(5)而言，當先驗模型所假定的雜波場景非高斯性較強，而實際探測環境非高斯性較弱時，換句話說，即檢測器所假定的探測環境比實際探測環境更“惡劣”時，檢測器在當前探測環境的性能必然優于其在“惡劣”環境下的探測性能。

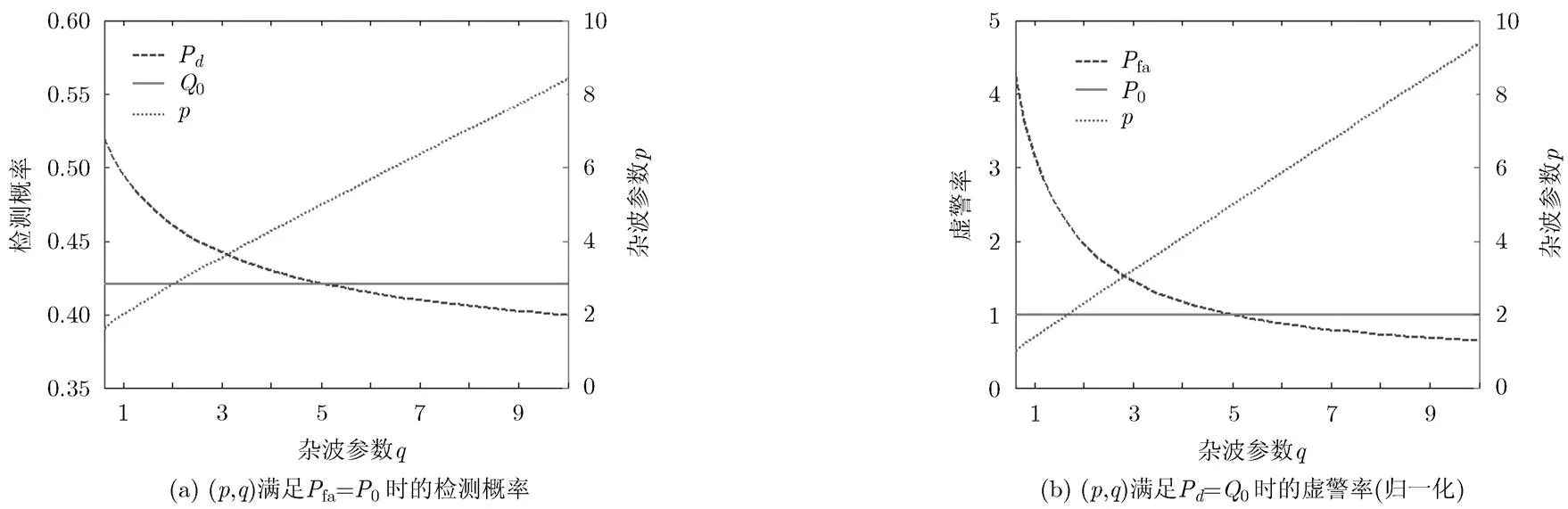
圖1 (p,q)滿足約束關系時的檢測器性能

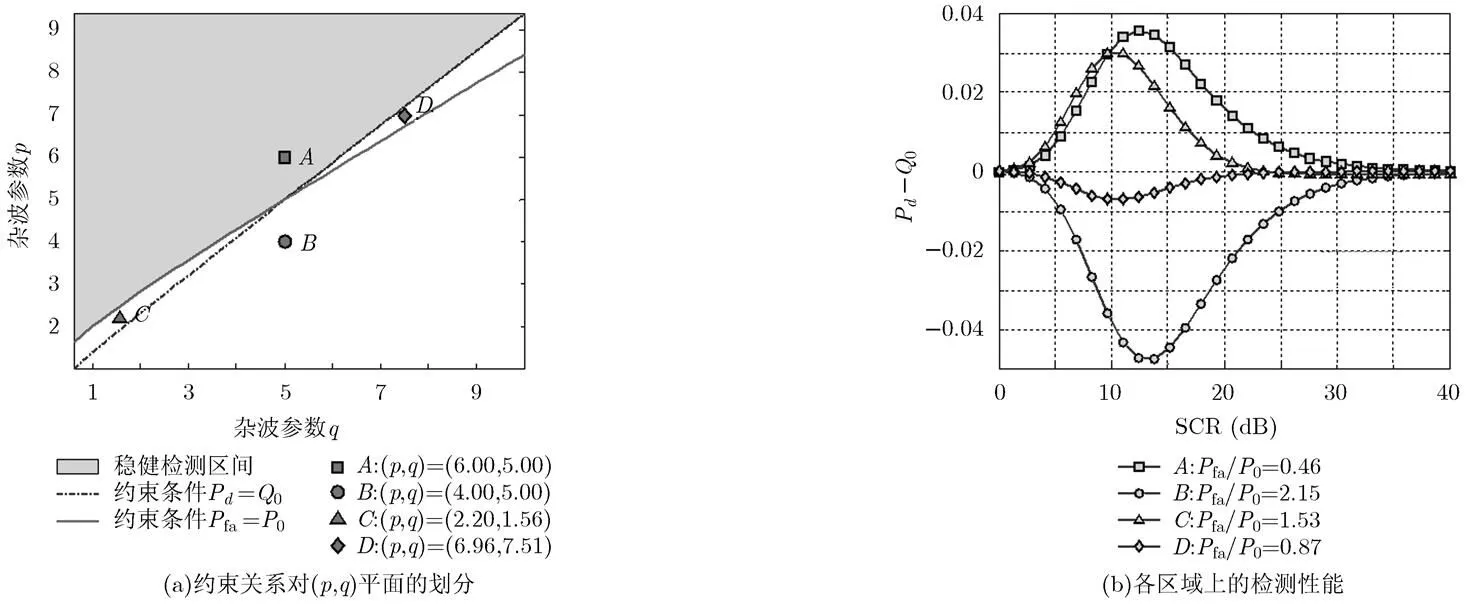
圖2 a=b=5時檢測器的敏感性分析

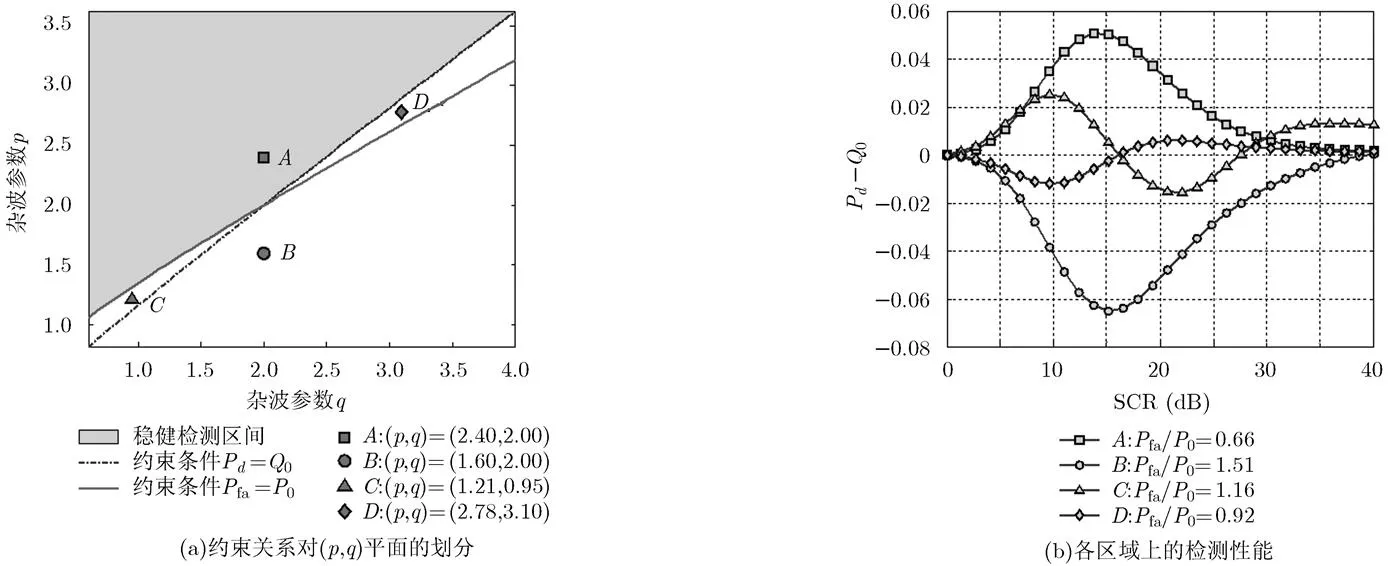
圖3 a=b=2時檢測器的敏感性分析

5 結論

知識輔助檢測器利用先驗信息提高檢測性能，然而先驗信息與當前探測環境不匹配時，檢測性能可能受到影響。本文考慮了基于逆伽馬分布紋理分量的復合高斯雜波下的知識輔助檢測器，給出了先驗模型參數失配條件下的虛警概率，Swerling I型目標的檢測概率的計算公式。分析了知識輔助檢測器在不同雜波場景參數下的敏感性，并獲得了雜波場景參數的穩健區間；在該區間內，雖然先驗模型參數與雜波場景模型參數不匹配，但檢測器具有更低的虛警率和更高的檢測概率。

[1] Carretero-Moya J, Menoyo J G, and Lopze A A. Small target detection in high resolution heterogeneous sea clutter: an empirical analysis[J]., 2011, 47(3): 1880-1888.

[2] Moya J C and Maio A D. Experimental performance analysis of distributed targets coherent radar detector[J]., 2012, 48(3): 2216-2238.

[3] Abramovich Y I and Besson O. Regularized covariance matrix estimation in complex elliptically symmetric distributions using the expected likelihood approach[R]. University of Toulouse-ISAE, December 2012.

[4] Gini F and Rangaswamy M. Knowledge-based Radar Detection, Tracking, and Classification[M]. USA, John Wiley & Sons Inc., 2008: 103-128.

[5] Wu Y, Tang J, and Peng Y. On the essence of knowledge aided clutter covariance estimate and its convergence[J]., 2011, 47(1): 569-585.

[6] Wang P, Li H, and Himed B. Knowledge-aided parametric tests for multichannel adaptive signal detection[J]., 2011, 59(12): 5970-5982.

[7] Wang P, Sahinoglu Z, and Pun M,.. Knowledge-aided adaptive coherence estimator in stochastic partially homogeneous environments[J]., 2011, 18(3): 193-196.

[8] Hao C, Orlando D, and Hou C. Persymmetric Rao and Wald tests for partially homogeneous environment[J]., 2012, 19(9): 587-590.

[9] Maio A D, Farina A, and Foglia A. Knowledge-aided Bayesian radar detectors & their application to live data[J]., 2010, 46(1): 170-183.

[10] Bidon S, Besson O, and Tourneret J Y. Knowledge-aided STAP in heterogeneous clutter using a hierarchical Bayesian algorithm[J]., 2011, 47(3): 1863-1879.

[11] 鄒鯤, 趙修斌, 田孝華, 等. 非高斯雜波中知識輔助的信號檢測算法[J]. 信號處理, 2012, 28(1): 60-66.

Zou Kun, Zhao Xiu-bin, Tian Xiao-hua,.. Knowledge- aided signal detection algorithm in non-Gaussian clutter[J]., 2012, 28(1): 60-66.

[12] 鄒鯤, 廖桂生, 李軍, 等. 基于Bayes框架的復合高斯雜波下穩健檢測[J]. 電子與信息學報, 2013, 35(7): 1555-1561.

Zou Kun, Liao Gui-sheng, Li Jun,.. Robust detection in compound Gaussian clutter based on Bayes framework[J].&, 2013, 35(7): 1555-1561.

[13] Bandiera D, Besson O, and Ricci G. Knowledge-aided covariance matrix estimation and adaptive detection in compound Gaussian noise[J]., 2010, 58(10): 5390-5396.

[14] Bandiera F, Besson O, and Ricci G. Adaptive detection of distributed targets in compound-Gaussian noise without secondary data: a Bayesian approach[J]., 2011, 59(12): 5698-5708.

[15] Shang X and Song H. Radar detection based on compound- Gaussian model with inverse gamma texture[J].,&, 2011, 5(3): 315-321.

[16] Balleri A, Nehorai A, and Wang J. Maximum likelihood estimation for compound-Gaussian clutter with inverse gamma texture[J]., 2007, 43(2): 775-779.

[17] Sangston K J, Gini F, and Greco M S. Coherent radar target detection in heavy-tailed compound Gaussian clutter[J]., 2012, 48(1): 64-77.

[18] Ollila W, Tyler D E, Koivunen V,.. Compound Gaussian clutter modeling with an inverse Gaussian texture distribution[J]., 2012, 19(12): 876-879.

鄒 鯤： 男，1976 年生，講師，從事雷達信號處理、統計信號檢測及其在雷達、導航方面的應用研究.

廖桂生： 男，1963 年生，教授，博士生導師，研究方向為空時自適應處理、天基預警和陣列信號處理等.

李 軍： 男，1972年生，副教授，研究方向為信號處理技術在無線通信中的應用.

Sensitivity Analysis of Knowledge Aided Detector in Non-Gaussian Clutter

Zou Kun①②Liao Gui-sheng①Li Jun①Li Wei②Li Tian-xing③

①(,,,710071,)②(,,,710077,)③(,100190,)

Prior information can be used to improve detection performance of knowledge aided detectors, but the detection performance may be affected by the mismatches between the prior information and current clutter environment. In this paper, the knowledge aided detector in compound Gaussian clutter is considered, for the inverse Gamma distribution is used as the prior distribution of clutter texture component, and the detection performance of this detector is analyzed with different clutter texture component model parameters. First, false alarm rate and detection probability of Swerling I target are given under the condition of mismatched prior information parameters. Second, the impact on the detection performance with clutter texture distribution parameters is analyzed under the conditions of given prior information parameters. Theoretical analysis results show that when the distribution parameters of clutter texture component are located in some area, the detection performance could be better than that with the prior information matchs the clutter environment. The computer simulation validates the conclusion.

Radar signal processing; Knowledge aided detector; Compound Gaussian; Inverse Gamma distribution; Mismatched prior information

TN957.51

A

1009-5896(2014)01-0181-06

10.3724/SP.J.1146.2013.00320

2013-03-15收到，2013-07-27改回

中國博士后科學基金(2012M521744)，國家自然科學基金(61271292)和陜西省自然科學基金(2011JQ8040)資助課題

鄒鯤 wyyxzk@163.com