基于Nuttall自卷積窗FFT算法的生物電阻抗譜多頻率同步測量方法

楊宇祥 張 甫 喬 洋 張 雯 溫 和 唐 求

?

基于Nuttall自卷積窗FFT算法的生物電阻抗譜多頻率同步測量方法

楊宇祥*①張 甫①喬 洋①張 雯①溫 和②唐 求②

①(西安理工大學機械與精密儀器工程學院 西安 710048)②(湖南大學電氣與信息工程學院 長沙 410082)

傳統的掃頻式生物電阻抗頻譜(BIS)測量法難以準確反映生物體真實的阻抗信息，開發BIS的多頻率同時快速測量方法具有重要意義。該文提出一種基于多頻率同步(MFS)信號激勵和加窗改進FFT算法的BIS多頻率同步快速測量方法。該文首先介紹了一種7頻率同步信號的合成及其頻譜特性，提出了性能優良的Nuttall自卷積窗函數，并構建了基于Nuttall自卷積窗的改進插值FFT諧波分析算法，從而在理論上論證了BIS多頻率同步快速測量的可行性，為下一步開發實際的BIS快速測量系統提供了技術支持。

生物電阻抗譜；多頻率同步信號；Nuttall自卷積窗；加窗插值FFT算法

1 引言

生物電阻抗譜(Bio-Impedance Spectroscopy, BIS)是指生物體在通過低于興奮閾值的交流弱電流時所表現出的導電特性和介電特性，它反映了微觀細胞層次的電特性[1]。通過BIS的測量可以了解被測組織的生理、病理狀態等豐富的功能信息，被認為是未來最具潛力的疾病早期診斷手段之一，近幾年在組織缺血監測[2]、乳腺癌診斷[3]、病人體液監測[4,5]、人體水合作用狀態評估[6]等方面獲得了成功的應用，預示著BIS技術在疾病的無創檢測、早期診斷、連續監護等方面的遠大的未來。

BIS技術以多頻率、復阻抗測量為基礎，當前流行的BIS測量法本質上都屬于掃頻測量法，即每次測量時注入單頻率激勵電流，從低頻到高頻依次掃頻完成測量，耗時較長[7]。而生物體的生理狀態受血流、心跳等因素的影響而連續快速動態變化，因此BIS的掃頻測量不能準確反映生物體在某一時刻的阻抗頻譜信息[8,9]。BIS測量技術的發展方向是多頻率同步快速測量法，即通過注入多頻率激勵電流，同時測得多個頻率點的阻抗信息，大大縮減測量時間，以更準確地反映被測體在某時刻的真實生理狀態[10,11]。

BIS多頻率同步測量的一大難點是如何產生合適的多頻率同步激勵信號源，本文作者前期提出了一種基于Walsh函數的多頻率同步(MFS)信號合成方法[12]，為BIS的多頻率同步測量確立了一種比較理想的激勵信號源[13]。本文主要探討基于MFS信號激勵的BIS多頻率同步測量方法，擬采用7頻率同步信號?(7,)作為激勵信號，提出一種旁瓣性能突出、主瓣性能優良的Nuttall自卷積窗函數，構建基于Nuttall自卷積窗的改進插值FFT諧波分析算法，研究基于加窗插值FFT算法的BIS測量方法，并設計BIS仿真測量實驗，驗證測量算法的可行性。

2 7頻率同步信號? (7, t)

根據文獻[12]介紹的MFS信號合成原理，選定=7，基于Walsh函數可合成7頻率同步信號(7,)：

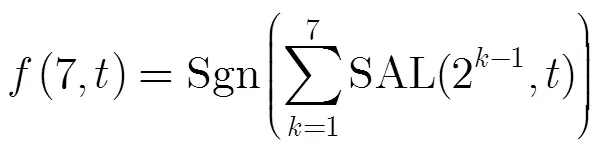
其中Sgn()表示符號函數：

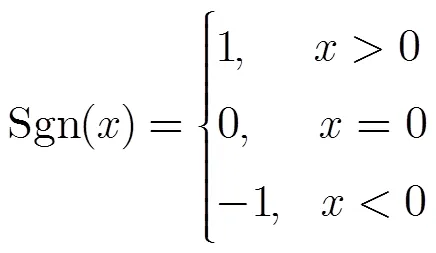
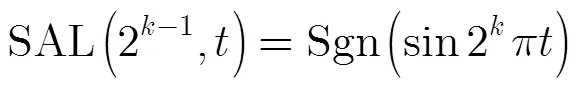
?(7,)在一個周期內由128個碼元組成，可以用向量表示為?(7,)= [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, -1, 1, 1, 1, 1, 1, 1, 1, -1, 1, 1, 1, -1, 1, -1, -1, -1, 1, 1, 1, 1, 1, 1, 1, -1, 1, 1, 1, -1, 1, -1, -1, -1, 1, 1, 1, -1, 1, -1, -1, -1, 1, -1, -1, -1, -1, -1, -1, -1, 1, 1, 1, 1, 1, 1, 1, -1, 1, 1, 1, -1, 1, -1, -1, -1, 1, 1, 1, -1, 1, -1, -1, -1, 1, -1, -1, -1, -1, -1, -1, -1, 1, 1, 1, -1, 1, -1, -1, -1, 1, -1, -1, -1, -1, -1, -1, -1, 1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1, -1]。(7,)在一個周期內的時域波形如圖1所示。

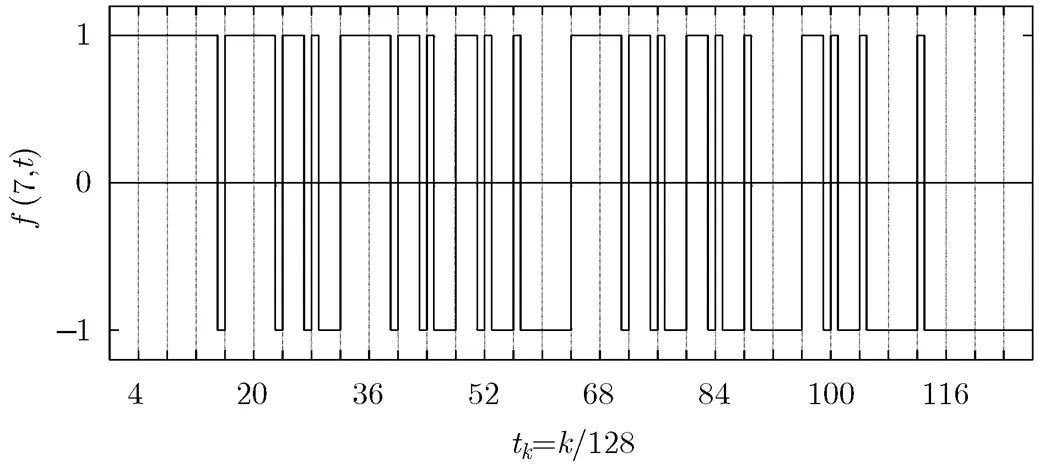
圖1 合成的?(7,t)在單位周期[0,1]上的波形

由圖2和表1可以看出：合成的7頻率同步信號?(7,)在BIS測量上具有如下優點：

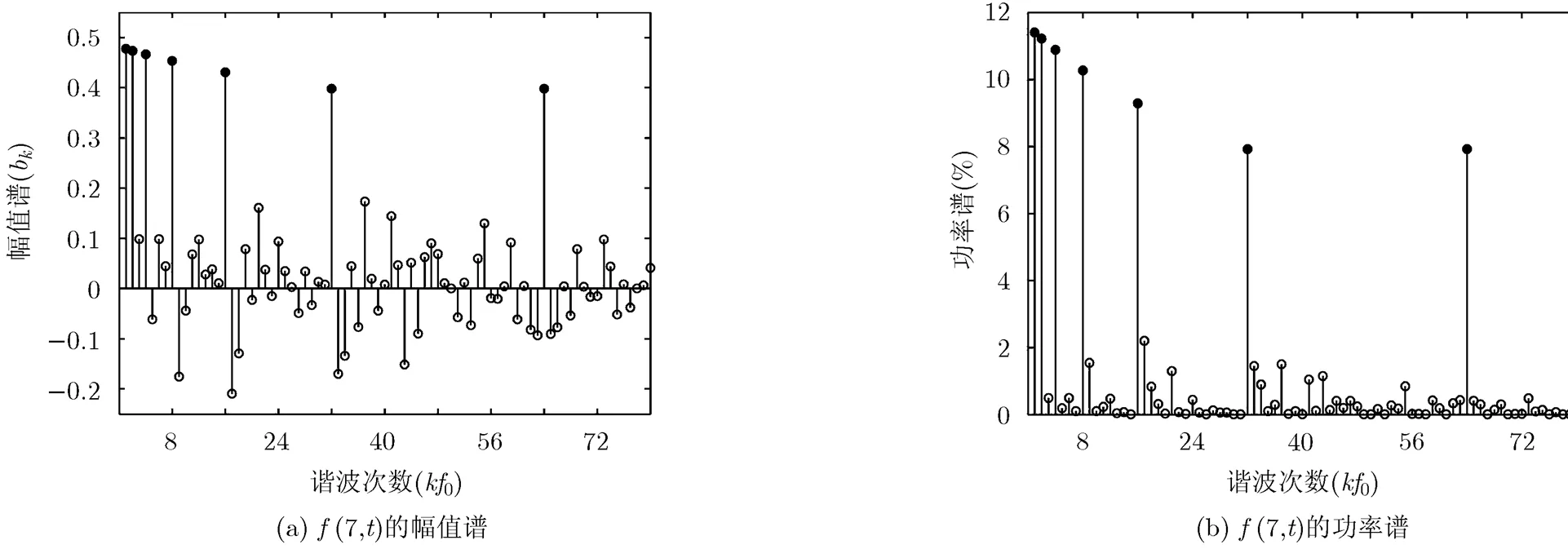
圖2 合成的?(7,t)的幅值譜和功率譜

表1 7頻率同步信號?(7,t)的主諧波Hk頻率特性

(1)信號本身含有7個幅值較大的主諧波分量信號，各主諧波分量的幅值基本相等，可保證BIS在主諧波頻率上進行等精度測量，信噪比高。

(2)主諧波分量信號的起始相位相同，非常有利于復阻抗相位的準確測量。

(3)主諧波分量的頻率按2步進，覆蓋的頻率范圍大，有利于提高Cole-Cole阻抗圓圖的擬合精度[14]。

3 基于Nuttall自卷積窗的改進插值FFT算法

BIS多頻率同步測量實質上是求解多頻率同步信號(,)中個主基頻點正弦分量的電壓幅值和相位，屬于諧波分析的范疇。快速傅里葉變換(FFT)算法是目前應用最廣泛的諧波分析算法。但由于嚴格的同步采樣和整周期采樣無法實現，FFT算法存在頻譜泄漏和柵欄效應，影響各頻率分量測量的準確度。

本文在長期研究加窗改進FFT算法[15]的基礎上，構建了頻譜函數簡單、旁瓣性能突出、主瓣性能優良的新型Nuttall自卷積窗函數，以減少頻譜泄漏和柵欄效應的影響，研究基于新型窗函數的改進插值FFT諧波分析算法。

3.1 Nuttall自卷積窗設計

Nuttall窗是一種余弦組合窗，其時域表示為

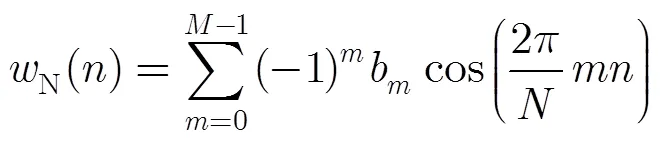
表2典型的Nuttall窗函數系數表

窗系數3項1階4項3階4項1階3項最小旁瓣4項最小旁瓣 b00.408970.3389460.3557680.42438010.3635819 b10.500000.4819730.4873960.49734060.4891775 b20.091030.1610540.1442320.07827930.1365995 b3-0.0180270.012604-0.0106411

4項3階Nuttall窗旁瓣峰值電平值低，旁瓣衰減速率最高，具有最優的旁瓣性能，因此本文選用4項3階Nuttall窗。

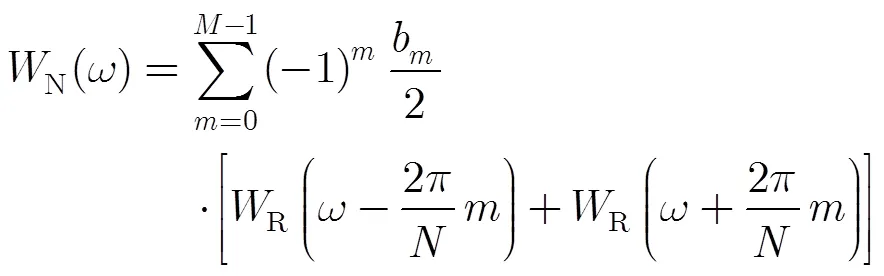
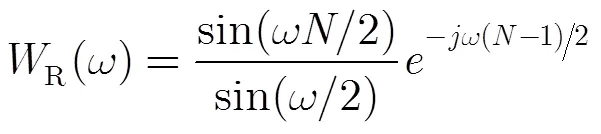
Nuttall自卷積窗定義為若干個相同的Nuttall窗進行時域卷積運算，階Nuttall自卷積窗可表示為

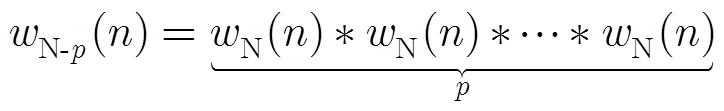
其中下標表示參與卷積運算的Nuttall自卷積窗的個數。

根據卷積定理，階Nuttall自卷積窗的頻譜函數為參與卷積的Nuttall窗的頻譜函數的次冪，即

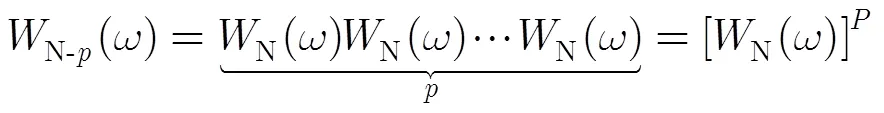
圖3給出了長度為的1~4階Nuttall自卷積窗的歸一化對數頻譜。

由圖3可見，Nuttall自卷積窗的旁瓣峰值電平與旁瓣衰減速率均和卷積階數成正比。這表明，隨著卷積階數的增加，Nuttall自卷積窗的旁瓣性能得到迅速提高。考慮到計算復雜度和計算時間，本文采用4階Nuttall自卷積窗對信號進行截短，以有效抑制頻譜泄漏。

3.2 基于Nuttall自卷積窗的改進插值FFT算法

設單一頻率正弦信號()經采樣后得到的離散序列()為

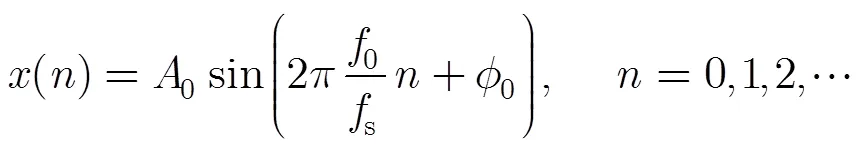
其中0, ?0,分別為信號的幅值、頻率和初相角；?s為采樣頻率。

對式(9)所示的()，用長度為的階Nuttall自卷積窗進行截斷，截短后信號的離散頻譜為

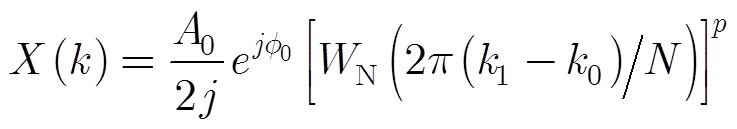
其中0= ?0/?代表頻率?0在離散頻譜中的位置。

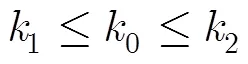
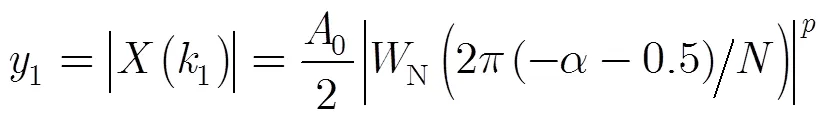
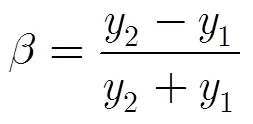
將式(11)，式(12)代入式(13)，可得

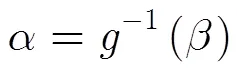
多項式最高次數=7時，加4階Nuttall自卷積窗后，頻譜插值多項式為

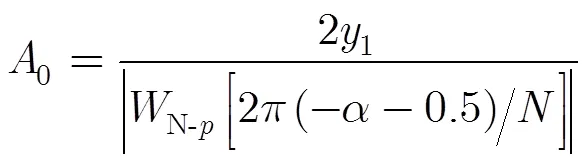
初相角為

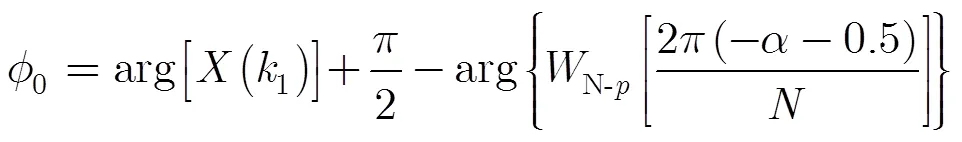
對于含有多個正弦諧波分量的多頻率同步信號，可以設置式(9)中的頻率?0等于某一特定頻率?，求出在頻率?下的諧波分量參數：幅值A和初相角。

4 結束語

開發BIS的多頻率快速測量具有重要意義。本文作者前期提出的多頻率同步(MFS)信號具有多種理想時域和頻域特性，非常適合作為BIS測量激勵信號。在此基礎上，本文發展了一種基于Nuttall自卷積窗改進FFT算法的BIS多頻率同步快速測量方法，提出了性能優良的Nuttall自卷積窗函數，構建了基于Nuttall自卷積窗的改進插值FFT諧波分析算法，并利用基于最小二乘法的多項式擬合方法，給出了離散頻譜插值多項式和諧波參數計算式，從而在理論上論證了BIS多頻率同步快速測量的可行性，為下一步開發實際的BIS快速測量系統提供了技術支持。

[1] Grimnes SMartinsen ? G. Bioimpedance and Bioelectricity Basics[M]. 2nd Edition, London: Elsevier Academic Press, 2008: 1-3.

[2] Mellert F, Winkler K, Schneider C,Detection of (reversible) myocardial ischemic injury by means of electrical bioimpedance[J]., 2011, 58(6): 1511-1518.

[3] Czerniec S A, Ward L C, Lee M J,Segmental measurement of breast cancer-related arm lymphoedema using perometry and bioimpedance spectroscopy[J]., 2011, 19(5): 703-710.

[4] Hur E, Usta M, Toz H,Effect of fluid management guided by bioimpedance spectroscopy on cardiovascular parameters in hemodialysis patients: a randomized controlled trial[J]., 2013, 61(6): 957-965.

[5] Parmentier S P, Schirutschke H, Schmitt B,Influence of peritoneal dialysis solution on measurements of fluid status by bioimpedance spectroscopy[J]., 2013, 45(1): 229-232.

[6] Utter A C, Mcanulty S R, Riha B F,The validity of multifrequency bioelectrical impedance measures to detect changes in the hydration status of wrestlers during acute dehydration and rehydration[J]., 2012, 26(1): 9-15.

[7] Min M, Paavle T, Annus P,Rectangular wave excitation in wideband bioimpedance spectroscopy[C]. Proceedings of the IEEE International Workshop on Medical Measurements and Applications, Italy, 2009: 268-271.

[8] Tao S, Holmes D, Gawad S,High speed multi-frequency impedance analysis of single particles in a microfluidic cytometer using maximum length sequences[J]., 2007, (8): 1034-1040.

[9] 鞠康, 何為, 何傳紅,等基于直接數字頻率合成的混合頻率恒流源設計[J]. 儀器儀表學報, 2010, 31(9): 2109-2114.

Ju Kang, He Wei, He Chuan-hong,.. Design of mixing frequency constant current source based on direct digital synthesizer[J]., 2010, 31(9): 2109-2114.

[10] Sanchez B, Schoukens J, Bragos R,Novel estimation of the electrical bioimpedance using the local polynomial method. Application to in vivo real-time myocardium tissue impedance characterization during the cardiac cycle[J]., 2011, 58(12): 3376-3385.

[11] Gordon R L R, Min M, Parve T,A virtual system for simultaneous multi-frequency measurement of electrical bioimpedance[J]., 2005, 7(1): 243-246.

[12] 楊宇祥, 呂林濤, 樂靜等基于Walsh函數的多頻率同步信號合成方法[J]. 儀器儀表學報, 2011, 32(7): 1540-1545.

Yang Yu-xiang, Lü Lin-tao, Le Jing,. Synthesis method of multi-frequency synchronized signals based on Walsh functions[J]., 2011,

32 (7): 1540-1545.

[13] Yang Y, Kang M, Lu Y,Design of a wideband excitationsource for fast bioimpedance spectroscopy[J]., 2011, 22(1): 013001.

[14] Seoane F, Ward L C, Lindecrantz K,Automated criterion-based analysis for Cole parameters assessment from cerebral neonatal electrical bioimpedance spectroscopy measurements[J]., 2012, 33(8): 1363-1377.

[15] 溫和, 滕召勝, 王永, 等. 改進加窗插值FFT動態諧波分析算法及應用[J]. 電工技術學報, 2012, 27(12): 270-277.

Wen He, Teng Zhao-sheng, Wang Yong,. Improved windowed interpolation FFT algorithm and application for power harmonic analysis[J]., 2012, 27(12): 270-277.

楊宇祥： 男，1974年生，博士，副教授，研究方向為生物醫學信號檢測與處理.

張 甫： 男，1990年生，碩士生，從事智能信息處理的研究.

溫 和： 男，1982年生，博士，副教授，研究方向為智能信息處理.

唐 求： 女，1970年生，博士，副教授，研究方向為智能信息處理.

Multi-frequency Synchronized Measurement Method of Bioimpedance Spectroscopy Based on Nuttall Self-convolution Windowed FFT Algorithm

Yang Yu-xiang①Zhang Fu①Qiao Yang①Zhang Wen①Wen He②Tang Qiu②

①(,’,’710048,)②(,,410082,)

Since the traditional frequency-sweeping based Bio-Impedance Spectroscopy (BIS) measurement method can not reflect accurately the true impedance of organism, the development ofmulti-frequency simultaneous fast measurement method of BIS has significance. A BIS Multi-Frequency Synchronized (MFS) measurement method is proposed based on MFS signal excitation and a windowed FFT algorithm. First, the synthesis of a seven-frequency synchronized signal, as well as its spectral characteristic, is introduced. Then, a Nuttall self-convolution window function with excellent performance is put forward, and the improved interpolation FFT-based harmonic analysis algorithm based on this window is built. It validates theoretically the feasibility of the proposed BIS Multi- Frequency Synchronized fast measurement method, and provides technical support for development of practical BIS fast measurement systems.

Bio-Impedance Spectroscopy (BIS); Multi-Frequency Synchronized (MFS) signal; Nuttall self- convolution window; Windowed interpolation FFT algorithm

TM938.84; R318.03

A

1009-5896(2014)01-0250-05

10.3724/SP.J.1146.2013.00348

2013-03-18收到，2013-07-18改回

國家自然科學基金(61273271, 30900317)，中國博士后科學基金(20110491674)和陜西省教育廳科學研究計劃(12JK0527)資助課題

楊宇祥 yangyuxiang@xaut.edu.cn