評價法在九龍江水體富營養化評價中的應用

陳秋平，胥思勤

（貴州大學喀斯特環境與地質災害防治教育部重點實驗室，貴州 貴陽 550003）

評價法在九龍江水體富營養化評價中的應用

陳秋平，胥思勤

（貴州大學喀斯特環境與地質災害防治教育部重點實驗室，貴州 貴陽 550003）

采集7個斷面水樣并監測了其總磷 （TP）、葉綠素 a（Chl－a）、高錳酸鉀指數 （CODMn）、總氮 （TN）。利用所得數據，采用模糊數學法綜合評價了九龍江 （薌城段）水體富營養化程度。結果表明：九龍江 （薌城段）富營養化基本為Ⅴ級，個別斷面富營養化為Ⅵ級或偏向Ⅵ級。

模糊數學；評價；富營養化；九龍江

水體富營養化評價早期以綜合評價法為主，但在評價標準和評價指標的選擇上很不完善，導致評價結果無法真實反映富營養化水平［1］。模糊數學法［2～8］采用隸屬函數來描述水質的分界，體現了實際界限的模糊性，避免了以往水質分級不連續的弱點，使評價結果更接近客觀實際。權重的大小根據超標多少確定，考慮了各項參數在總體污染中的作用差異，而且最終結果不僅能夠反映出水體的水質級別，還能反映出該水體對應于各級水質的隸屬情況。目前國內外富營養化的評價中，大多選擇與富營養化過程密切相關的因子作為評價參數［9］。

本文采用最大隸屬度原則和加權平均法相結合來進行模糊綜合評價，將其應用于九龍江 （薌城段）水體富營養化評價。

1 模糊評價數學模型的建立

1.1 建立評價對象的因素集

因素集 U是參與評價的 n個污染因子的實測濃度組成的模糊子集。

1.2 建立評價集

評價集 V是與 U中評價因子相應的環境質量標準等級的集合。

1.3 確定評價因素的模糊權向量

通常各因子的重要程度不同，因此對每個因子ui賦于一個相應的權重ai（i＝1，2，…，n）構成權重集A。根據公式（1）確定單項因子權重值 wi。

式中：ci－因子 ui的實測濃度值；si－因子ui各級環境標準的算術均值；wi－因子 ui的權重值。

在模糊綜合評價中，ai本質上是因子 ui對被評價事物的重要程度。為進行模糊運算，對各項因子的權重值進行歸一化運算得出因子的權重ai。

上述 n項因子指標，分別計算出權重后，組成一個l×n模糊權重集：A＝{a1，a2，…ai…，an}。

1.4 確定單因素評價矩陣 R進行單因素模糊評價

1.4.1 隸屬度的確定

從一個 ui出發進行評價，以確定評價對象對評價集元素 vi的隸屬程度 rij(j＝1，2，．．．，m)稱為單因素模糊評價。

ui屬于第1級水質的隸屬函數為：

ui屬于第j級水質的隸屬函數為：

ui屬于第n級水質的隸屬函數為：

式中：rij－因子 ui對j級水質的隸屬度；ci－因子ui的實測濃度值；si，j－因子ui第 j級水質標準。

對第 i個因子uj評價的結果組成單因素模糊評價集

1.4.2 單因素評價矩陣R

根據以上計算過程，可得到相應于每個因子的單因素模糊評價集：

若共有 n項水質參數 m級水質標準，將各單因素模糊評價集 Rj的隸屬度為行組成單因素評價矩陣，則可得到n×m階的模糊矩陣R。

R的第 i行表示第 i個因子影響評價對象時對各個評價元素的隸屬程度；第j列表示所有因子影響評價對象取第j個評價元素的隸屬程度。

1.5 綜合評價

單因素模糊評價僅反映一個因子對評價對象的影響，而未反映所有因子的綜合影響。模糊綜合評價考慮所有因子的影響，將模糊權向量 A與單因素模糊評價矩陣 R復合，得到模糊綜合評價向量B［10］。

式中：bj稱為評價指標。

將上述 A、R矩陣進行復合運算，算法與普遍矩陣類似，只將矩陣乘法運算中的加號 “＋”改為“V”，將乘號“·”改為“＾”。“V”的意義為取加數中最大者為 “和”，“＾”的意義為取相乘兩數較小者為 “積”。

此結果為對應于各級水質的隸屬度，最后取其中最大者所對應的水質級數，作為該水體的綜合評價級數［11］。當其它等級隸屬度的總和超過了最大隸屬度，不適于用最大隸屬度原則，采用加權平均法來解決［10］。其計算公式為：

式中：bj－隸屬于第j級水的隸屬度；k－待定系數 （k＝1或 2），目的是控制較大 bj所起的作用，本文取k＝1。

2 模糊綜合評價的應用

2.1 數據來源

本文對九龍江 （薌城段）進行監測斷面設置（見圖1）和布點監測，經統計整理后作為評價的基礎資料。采用各監測斷面實測數據（見表1）進行模糊處理。

表1 九龍江 （薌城段）地表水水質監測結果 （mg／L）

2.2 參數選擇

根據我國湖庫營養化評價標準，并考慮九龍江的特點，按照監測數據和主要污染物的代表性，選擇總磷（TP）、葉綠素 a（Chl－a）、高錳酸鉀指數（CODMn）、總氮 （TN）4個參數作為評價因子，即評價對象的因素集U＝｛TP，Chl－a，CODMn，TN｝。

2.3 確定評價標準

參照我國湖庫營養化評價標準 （見表 2），把九龍江富營養化分為 6級。即評價集為：V＝ ｛I，II，III，IV，V，VI｝。

表2 我國湖庫營養化評價標準（mg／L）

2.4 計算各參數的隸屬度，建立模糊關系矩陣 R

取因素集 U＝｛TP，Chl－a，CODMn，TN｝，評價集用實測濃度值分別求出不同級別水的隸屬度r。

以洋老洲沙灘斷面TP為例。其實測濃度為0.21mg／L，介于V級和Ⅵ級之間。根據公式 （3）可得 TP對各級營養化的隸屬度。

求出隸屬6個級別的隸屬度 r分別為：

同理可得洋老洲沙灘斷面其它3項指標6個級別的隸屬度 （見表3），建立模糊關系矩陣R。根據以上步驟，可計算出其它監測斷面的模糊關系矩陣R。

表3 洋老洲沙灘斷面各參數的隸屬度

2.5 建立模糊權重集 A

2.5.1 各單項參數權重值的確定

以洋老洲沙灘斷面 TP為例，根據公式 （1）可得：

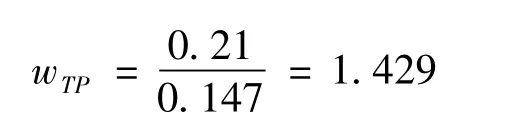
同法可求得其它3項參數的權重值。

WChl－a＝0.067，WCODMn＝1.832，WTN＝1.189 2.5.2確定各單項參數權重

根據公式 （2），可得：

同理可計算出洋老洲沙灘斷面其它 3個單項參數的權重，并組成一個 l×4的權重集 A＝（0316，0.015，0.405，0.263）。根據以上步驟，可計算出其它7個監測斷面各單項參數的權重，結果見表4。

表4 各監測斷面單項參數權重

2.6 綜合評價

根據公式（5），將權重集A和單因素模糊矩陣R復合，可得洋老洲沙灘斷面的綜合評價向量B。

因此，洋老洲沙灘斷面評價結果為：對 I級、Ⅱ級、Ⅲ級、Ⅳ級、V級、Ⅵ級水體營養化的隸屬度依次是 0，0.015，0，0.16，0.405，0.182，可見對Ⅳ級水體營養化的隸屬度最大而 V級僅次之。根據模糊綜合評價的最大隸屬度原則，可知洋老洲沙灘斷面為Ⅳ級水。同理可得其它斷面綜合評價向量B，結果見表5。

根據模糊綜合評價的最大隸屬度原則，由表5可知洋老洲沙灘和新橋均為 V級；但對于洋老洲可樂園、舊橋、戰備大橋、下洲村、漳州大橋斷面，采用加權平均法進行最后的綜合評判。計算得到 B*分 別 為 5.219，5.365，6.056，5.744，5.396，所以洋老洲可樂園富營養化級別Ⅴ級；舊橋營養化級別Ⅴ級；戰備大橋富營養化級別Ⅵ級；下洲村富營養化級別Ⅴ級，偏向Ⅵ級；漳州大橋富營養化級別Ⅴ級。

表5 各監測斷面隸屬度營養化級別計算表

3 結語

本文采用最大隸屬度原則和加權平均法相結合來進行模糊綜合評價，將其應用于九龍江 （薌城段）水體富營養化評價。結果表明：九龍江 （薌城段）水體富營養化基本為Ⅴ級，個別斷面營養化為Ⅵ級或偏向Ⅵ級。

［1］胡著邦，徐建民，全為民.模糊評價法在湖泊富營養化評價中的應用 ［J］.農業環境護，2002，21（6）：535－536.

［2］劉晨，鮑治宇.秦淮新河 （雨水段）水質的模糊數學評價 ［J］.蘇州科技學院學報 （工程技術版），2005，18（3）：57－60.

［3］趙紅.渭河水質評價及污染防治對策［J］.西北水資源與水工程，2003，14（1）：28－31.

［4］熊德琪.一種新的海水營養化模糊評價方法 ［J］.海洋通報，1993，12（6）：30－35.

［5］丁桑嵐.環境評價概論 ［M］.北京：化學工業出版社，2001.

［6］賀仲雄.模糊數學及其應用［M］.天津：天津科技出版社，1998.

［7］胡永宏，賀思輝.綜合評價方法 ［M］.北京：科學出版社，2000.

［8］謝季堅，劉承平.模糊數學方法及其應用 ［M］.武漢：華中理工大學，2000.

［9］黃文鈺，舒金華，吳延根.中國主要水庫富營養化評價 ［J］.貴州環保科技，1997，（2）：12－16.

［10］賈陳忠，秦巧燕，張竹清，等.模糊數學在地表水環境質量評價中的應用 ［J］.北方環境，2004，29（6）：73－77.

［11］王淑文，劉臣.水環境質量評價的模糊數學法［J］.吉林水利，2001（2）：20－22.

［12］高洪生，張玉珍.九龍江主要控制斷面水質評價與變化特征分析 ［J］.亞熱帶資源與環境報，2011，6（2）：42－48.

［13］張婷，劉靜玲，王雪梅.白洋淀水質時空變化及影響因子評價與分析 ［J］.環境科學學報，2010，30（2）：261－267.

Application of Fuzzy Mathematic Method on Evaluating Water Entrophication of Jiulong River

CHEN Qiu－ping，XU Si－qin
（Key Laboratory of Karst Environment and Geohazard Prevention，Ministry of Education，Guizhou Guiyang 550003 China）

The water was sampled from seven sections of Jiulong River.The total phosphorus（TP），chlorophylla，total nitrogen（TN），CODmn were tested.Fuzzy mathematic method was employed to assess the water entrophication of Xiangcheng section in Jiulong River.The results showed that the water entrophication was the fifth grade，and one of seven sections can reach the fourth grade.

fuzzy mathematics；evaluation；entrophication；Jiulong River

X82

A

1673－9655（2014）02－0039－04

2013－12－17

陳秋平 （1986－），男，碩士研究生，主要從事環境工程方面研究。

胥思勤，女，副教授，碩士生導師。