星載多基線InSAR理想相位圖的快速仿真方法

葛仕奇 劉光炎

?

星載多基線InSAR理想相位圖的快速仿真方法

葛仕奇*劉光炎

(南京電子技術研究所 南京 210039)

針對星載多基線干涉合成孔徑雷達(InSAR)系統，該文研究并提出了基于數字高程模型(DEM)數據、衛星軌道和基線信息的干涉相位的快速仿真方法。利用前向地理編碼進行星載InSAR幾何約束下的DEM模型匹配，完成多基線InSAR干涉相位生成，并通過多項式近似和混合迭代實現對模型匹配過程的優化。理論分析和仿真實驗表明，該方法在顯著提高計算效率的同時，保持了較高的相位生成精度，并且對復雜DEM模型有很好的迭代收斂性，適于實現對大場景復雜地形的星載多基線干涉相位快速仿真。

干涉合成孔徑雷達；多基線；相位仿真；地理編碼

1 引言

星載干涉合成孔徑雷達(InSAR)能夠全天時、全天候地提取大范圍地區的數字高程模型(DEM)[1]，而多基線InSAR技術通過對多通道數據的聯合處理，可以降低相位解纏難度并提高DEM的提取精度[2,1]，是航天對地觀測領域的研究熱點之一。干涉數據仿真在星載多基線InSAR系統設計中十分重要，其最基本的方法是以SAR回波仿真為基礎[4]，這種方法對體散射、有限信噪比等非理想因素的模擬最接近實際情況，但是運算量巨大，且由于處理環節多而不適于控制相位生成精度。本文主要研究基于場景DEM數據、衛星軌道和基線信息直接生成多基線干涉相位圖，利用這種方法可以得到精確反映地形變化的相位信息，因而可準確預測不同基線長度和傾角等系統參數下的干涉條紋特性、雷達圖像中的疊掩和陰影區域、以及局地幾何去相干等信息[5]，為系統優化設計提供依據；另外對仿真干涉相位可以定量引入后向散射模型和噪聲模型，便于對相位解纏、高程反演等算法進行可控誤差分析，從而實現對算法性能的定量評估[6]。此外，利用該方法生成的高精度地形參考相位，還可以應用于差分干涉SAR系統的信號處理中，具有較為廣泛的應用范圍。

對于干涉相位圖的仿真，常用方法是對已知DEM數據進行坐標變換，得到DEM均勻柵格點在雷達圖像坐標系中的映射點并賦予對應的干涉相位[7]，但是該方法涉及非均勻插值重采樣，不僅降低了仿真精度，而且增加了運算負擔。文獻[5]提出了一種可用于大場景的常規InSAR相位快速仿真方法，其核心思想是利用多項式快速生成算法和對稀疏采樣點的內插降低運算量。文獻[8]進一步研究了在星載立體、雙基地干涉模型下的干涉相位生成問題，并分析了相位生成精度。在多基線InSAR相位圖仿真方面，文獻[9,10]提出了多基線InSAR系統的相位仿真方法，該方法以機載模型為基礎，不適用于星載SAR構像模型下的干涉相位生成。本文在深入研究星載雷達成像系統嚴密構象模型的基礎上，提出了一種基于前向地理編碼的星載多基線InSAR干涉相位圖快速仿真方法，該方法可以在保證相位生成精度的同時，顯著提高運算效率，最后通過對仿真實驗，驗證了該方法的有效性。

2 星載多基線InSAR干涉相位生成原理

2.1 星載InSAR嚴密構像模型

在圖1所示的星載多基線InSAR系統中，一般以主星為參考，兩顆輔星獲得的SAR影像均根據主星成像結果進行配準生成干涉相位。相應地，在InSAR相位仿真中，首先需要精確建立主星成像平面中各采樣點與場景DEM數據間的映射關系，這一過程可基于星載雷達圖像的構像模型通過坐標變換來實現[11]。目前國內外采用的雷達圖像構像模型有Leberl模型，Konecny模型和距離-多普勒模型(R-D模型)等[12]，其中R-D模型可以直接利用星歷數據，根據雷達成像時的距離條件和多普勒頻移條件，建立SAR成像瞬間嚴格的物像關系，在地固坐標系(ECR)中可用3個方程共同描述該模型，即距離方程：

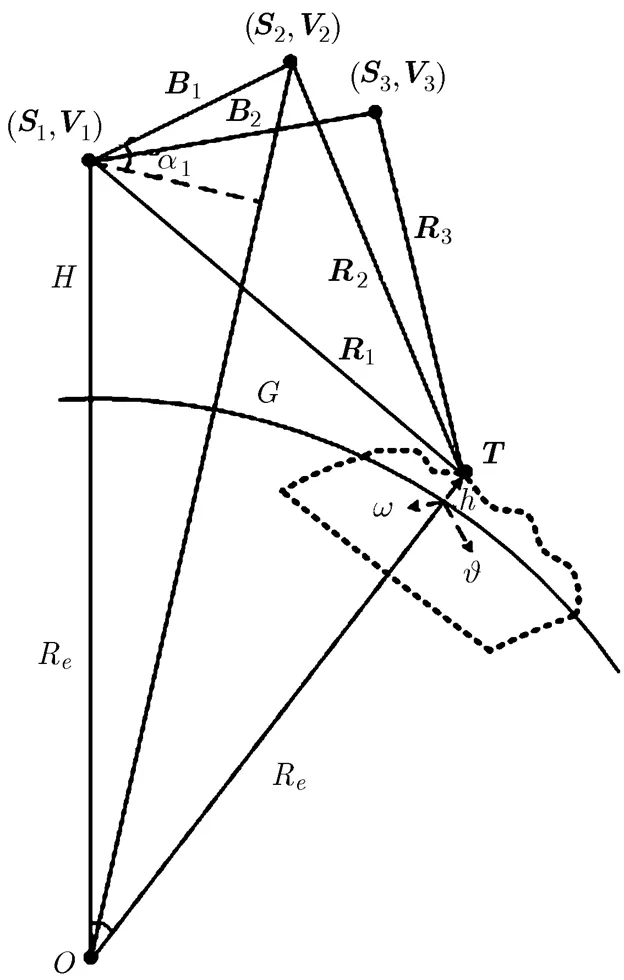
圖1星載多基線InSAR系統幾何構型圖

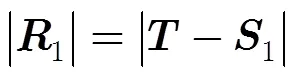
多普勒方程：

以及地球橢球模型方程：

基于R-D模型，能夠建立成像目標點在主星雷達圖像坐標與場景地理坐標之間的非線性映射關系，接下來還需要進一步根據基線信息完成多基線InSAR相位的生成。

2.2 多基線干涉相位生成

輔星軌道高度方程：

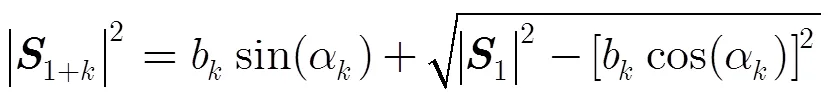
以及輔星多普勒方程：

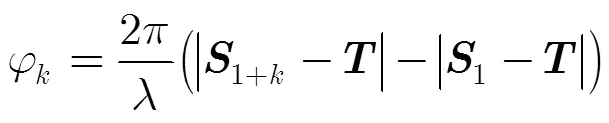
3 大場景星載InSAR相位圖的快速生成方法

基于上述原理，本文提出了一種高效的星載多基線干涉相位仿真方法，實現流程如圖2。

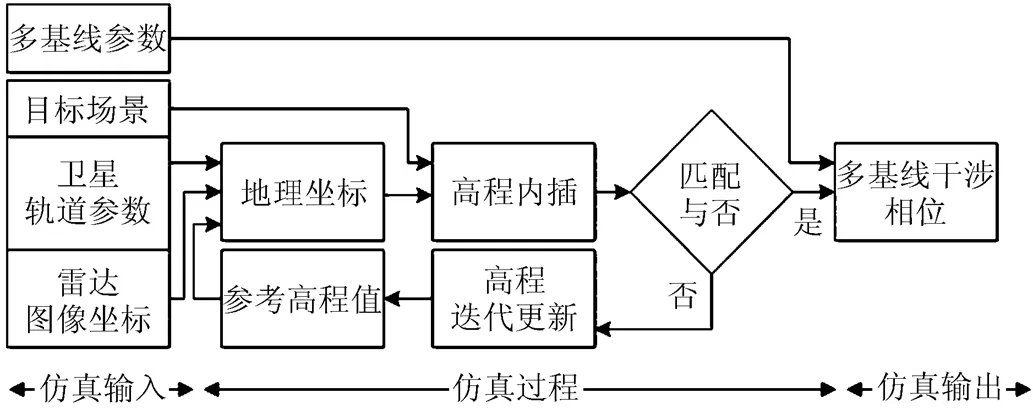
圖2 基于前向地理編碼的星載多基線干涉相位仿真流程圖

從計算的角度看，解上述兩個方程組需要解非線性空間的幾何方程組，而且式(1)~式(3)的求解嵌套在匹配定位過程中，這些計算都需要迭代處理，隨著仿真場景的增大，計算時間將迅速增加，故需要對前向地理編碼和匹配定位過程做進一步優化。

3.1 前向地理編碼的優化

其中，系數和可以由個假定高程及其對應的定位結果經多項式擬合獲得，而階數取決于對多項式近似誤差的分析。根據圖1，目標點地距為

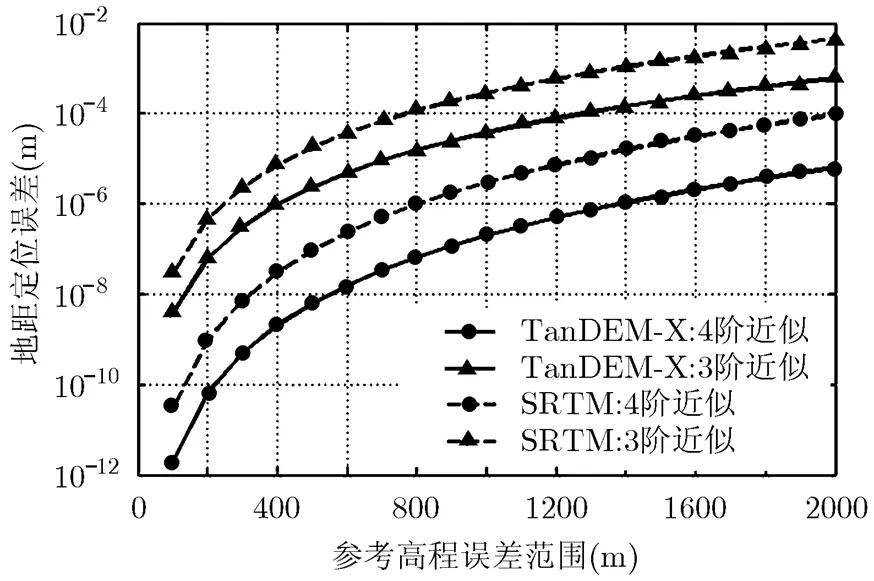
圖3 InSAR定位誤差隨參考高程誤差的分布曲線

3.2 匹配定位的快速實現

匹配定位中需要迭代更新參考高程，常規方法是采用不動點迭代( Fixed Point Iteration,

第1步 構造匹配目標函數

第3步 通過混合迭代算法逐步縮小解區間范圍，以最佳逼近DEM曲面。在混合迭代中，首先按照式(11)對目標函數進行反二次插值，如果插值結果使目標函數的絕對值減小了，并且使解區間至少減半，那么就以插值結果更新解區間邊界。

否則，按照式(12)對目標函數進行割線插值，并采用與之前同樣的準則判定是否用插值結果更新解區間邊界。

如果割線插值也失敗，最后可利用當前解區間的均值重新定界：

由于反二次插值和割線插值分別實現了對場景局部曲面的二次擬合和線性擬合，而均值定界是基于二分法的原理，因此收斂速度依次降低；但是，高階插值存在發散的可能，而均值插值可以保證解的收斂性，故采用混合迭代可以保證對復雜地形的高效率匹配。

4 仿真實驗及分析

表1星載InSAR系統參數

軌道高度(km)下視角(°)PRF(Hz)干涉圖分辨率(m) 511.9735.53832.53×3

實驗1對圖4(a)所示的多山DEM模型進行仿真分析，場景最高點為81.06 m。系統工作期間的空間基線變化保持在5%以內，且基線長度分別在406.9 m和634.6 m附近變化。

首先采用混合迭代得到的匹配定位輸出結果如圖4(b)所示，然后根據動態變化的基線信息計算不同時刻的輔星位置后，可得到干涉相位仿真結果，如圖5所示。可見，實驗結果正確反映了地形和基線對干涉條紋的影響。

實驗2在系統參數不變的情況下，對圖6(a)所示的某山區實際DEM數據進行仿真，最高點為112.34 m。由于該場景地形起伏更加復雜，可驗證本文方法的效率和收斂性，圖6 (b)為仿真得到的干涉相位圖(左)以及去平地相位圖(右)。

作為對比，表2給出了不同收斂閾值情況下，采用FPI方法和本文方法在平均迭代次數和發散點數方面的比較。可見FPI方法存在不同程度的迭代發散現象，而本文方法不存在該問題，而且具有較高的匹配效率。

圖4 實驗DEM模型

圖5 仿真DEM模型的多基線干涉相位(圖像大小512×512點，分辨率3 m)

圖6 實際DEM模型及干涉相位仿真結果(圖像大小512×512點)

最后，分析本文方法的效率，第1步通過預處理生成前向地理編碼多項式，第2步采用混合迭代法完成匹配定位，而第3步根據動態基線信息生成干涉相位。表3比較了優化前后各步運算的耗時，優化前的方法在FPI迭代過程中又嵌套了解方程組式(1)~式(3)所需進行的牛頓-拉費森迭代，計算效率極低。經優化后，不僅通過混合迭代降低了匹配定位的迭代次數，而且通過增加對前向地理編碼多項式的系數擬合這個預處理步驟，使單次迭代的運算量顯著減小。此外，通過均勻抽取控制點并計算得到干涉相位真值，以此為標準統計分析干涉相位生成精度，可得干涉相位的誤差均方根值為0.000559 rad。

表2 迭代性能比較

表3干涉相位仿真效率分析

值得注意的是，一旦預處理和匹配定位完成，對星載多基線InSAR系統可重復利用前兩步得到的定位結果，快速實現不同基線情況下的理想干涉相位圖仿真。

5 結束語

星載多基線InSAR是對常規InSAR技術擴展后形成的一種新型航天對地觀測手段，干涉相位圖仿真在該新興技術的研究中具有十分重要的意義。本文針對星載多基線InSAR系統構型，提出了一種基于前向地理編碼的多基線干涉相位圖快速仿真方法，該方法不僅提高了仿真效率，而且對復雜地形的干涉相位仿真有較好的收斂性，為星載多基線干涉相位圖的進一步應用研究奠定了基礎。后續工作還需考慮疊掩和陰影對干涉圖的影響，疊掩是指當迎坡坡度大于雷達下視角時，可能出現幾何上的多個點被疊加為一個點的情況；陰影是指當背坡坡度大于雷達俯角時，雷達波束被遮擋而無法到達的區域。下一步工作應分別進行疊掩和陰影區的識別與標注，從而更準確地反映輸入場景在給定系統參數下的干涉相位圖。

[1] Chang Wen-yen, Wang Chih-tien, Chu Chih-yuan,.. Mapping geo-hazard by satellite radar interferometry[J]., 2012, 100(10): 2835-2850.

[2] Yu Han-wen, Li Zhen-fang, and Bao Zheng. A cluster-analysis-based efficient multibaseline phase unwrapping algorithm[J]., 2011, 49(1): 478-487.

[3] Yuan Zhi-hui, Li Fei, Deng Yun-kai,.. Multichannel InSAR DEM reconstruction through closed-form robust Chinese remainder theorem[C]. IEEE International Conference on Geoscience and Remote Sensing Symposium (IGARSS), Munich, 2012: 4006-4009.

[4] He Zhi-hua, He Feng, Dong Zhen,.. Real-time raw-signal simulation algorithm for InSAR hardware-in-the-loop simulation applications[J]., 2012, 9(1): 134-138.

[5] Eineder M. Efficient simulation of SAR interferograms of large areas and of rugged terrain[J]., 2003, 41(6): 1415-1427.

[6] 李文強, 李景文, 陳杰. 一種干涉SAR復圖像數據的快速仿真方法[J]. 北京航空航天大學學報, 2005, 31(1): 32-35.

Li Wen-qiang, Li Jing-wen, and Chen Jie. Fast simulation of complex image for interferometric SAR[J]., 2005, 31(1): 32-35.

[7] Goblirsch W. The exact solution of the imaging equations for crosstrack interferometers[C]. IEEE Proceedings of International Geoscience and Remote Sensing Symposium, Singapore, 1997: 439-441.

[8] 王青松, 黃海風, 董臻, 等. InSAR 理想干涉相位計算的快速方法及精度分析[J]. 系統仿真學報, 2009, 21(18): 5951-5954.

Wang Qing-song, Huang Hai-feng, Dong Zhen,.. Fast simulation of InSAR ideal interferometric phase and precision analysis[J]., 2009, 21(18): 5951-5954.

[9] 張紅敏, 靳國旺, 徐青, 等. 多基線InSAR干涉圖仿真方案設計與分析[J]. 系統仿真學報, 2012, 24(7): 1516-1522.

Zhang Hong-min, Jin Guo-wang, Xu Qing,.. Design and analysis of interferograms simulation methods for multi-baseline InSAR[J]., 2012, 24(7): 1516-1522.

[10] Zhang Hong-min, Jin Guo-wang, Xu Qing,. Simulation of interferograms for multi-baseline InSAR study[C]. 2nd Asian-Pacific Conference on Synthetic Aperture Radar, Xi’an, 2009: 408-411.

[11] Frey O, Santoro M, Werner C,.. DEM-based SAR pixel-area estimation for enhanced geocoding refinement and radiometric normalization[J]., 2013, 10(1): 48-52.

[12] Xu Hua-ping, and Kang Changhui. Equivalence analysis of accuracy of geolocation models for spaceborne InSAR[J]., 2010, 48(1): 480-490.

[13] 仇曉蘭, 韓傳釗, 劉佳音. 一種基于持續運動模型的星載SAR幾何校正方法[J]. 雷達學報, 2013, 2(1): 54-59.

Qiu Xiao-lan, Han Chuan-zhao, and Liu Jia-yin. A method for spaceborne SAR geolocation based on continuously moving geometry[J]., 2013, 2(1): 54-59.

[14] Kim M and Hwang C. A polynomial-based ortho-rectification for SAR imagery[C]. 5th International Congress on Image and Signal Processing (CISP), Chongqing, 2012: 997-1000.

[15] Geudtner D, Zink M, Gierull C,.. Interferometric alignment of the X-SAR antenna system on the space shuttle radar topography mission[J]., 2002, 40(5): 995-1006.

[16] Zink M. TanDEM-X mission status[C]. IEEE International Conference on Geoscience and Remote Sensing Symposium (IGARSS), Munich, 2012: 1896-1899.

[17] 郭交, 李真芳, 劉艷陽, 等. 基于粗數字高程模型信息的干涉相位圖生成方法[J]. 電子與信息學報, 2010, 32(11): 2642-2647.

Guo Jiao, Li Zhen-fang, Liu Yan-yang,.. Approaches to interferogram generation based on coarse DEM[J].&, 2010, 32(11): 2642-2647.

葛仕奇： 男，1984年生，博士，研究方向為干涉合成孔徑雷達、實時信號處理等.

劉光炎： 男，1967年生，研究員，研究方向為信號處理、SAR/ InSAR系統設計及成像等.

Fast Simulation Method of Ideal Phase Map for Spaceborne Multi-baseline InSAR

Ge Shi-qi Liu Guang-yan

(,210039,)

Based on Digital Elevation Mode (DEM) data, satellite orbit and baseline information, a kind of fast interferometric phase simulation method is investigated and presented for spaceborne multi-baseline InSAR system. By taking advantage of forward geocoding, the match of DEM model under strict spaceborne InSAR geometry is utilized to realize multi-baseline interferometric phase generation, and the match process is further optimized by polynomial approximation and hybrid iteration. Theory analysis and simulation experiments indicate that the proposed method can improve the computation efficiency with enough phase accuracy, as well as better iteration convergence property for complicated DEM model. Consequently, the method is suitable for efficient simulation of spaceborne multi-baseline InSAR interferometric phase for large and rugged terrain.

Interferometric SAR (InSAR); Multi-baseline; Phase simulation; Geocoding

TN959.3

A

1009-5896(2014)03-0571-06

10.3724/SP.J.1146.2013.00604

2013-05-03收到，2013-11-08改回

葛仕奇 raymond2464@126.com