一種基于正則化的邊緣定向插值算法

季成濤 何小海 符耀慶 梁子飛 卿粼波

?

一種基于正則化的邊緣定向插值算法

季成濤①何小海*①符耀慶②梁子飛①卿粼波①

①(四川大學電子信息學院 成都 610065)②(中海油能源發展股份有限公司北京分公司 北京 100027)

針對傳統的基于線性回歸模型插值算法不能對變化劇烈的邊緣進行有效插值的問題，該文提出一種基于正則化的邊緣定向插值算法。算法主要分為兩部分：參數估計部分與數據估計部分。在參數估計部分，為了更加準確地描述圖像局部結構，把已估計的高分辨率像素作為訓練像素的一部分，用以進行回歸模型參數的估計。在數據估計部分，引入像素平滑方向作為正則化項，以降低參數的誤估計引起的數據估計偏差。實驗結果表明，該算法能很好地保持圖像的邊緣特征，尤其在變化比較劇烈的邊緣區域；與雙三次插值算法及基于正則化的局部線性回歸插值算法(Regularized Local Linear Regression, RLLR)相比，該算法能取得更好的視覺效果及較高的PSNR值。

圖像處理；插值；回歸模型；訓練像素；正則化

1 引言

圖像插值，是對已知的低分辨率(Low Resolution, LR)圖像通過一定的算法獲得高分辨率(High Resolution, HR)圖像的過程。圖像插值在很多領域得到了廣泛的應用，如消費電子設備、計算機視覺、遙感技術應用、醫學圖像處理等。傳統的圖像插值算法有最近鄰插值、雙線性插值、雙三次插值等[1,2]，這些插值方法的優點是計算簡單，運行時間少，但由于這些算法的插值濾波器有著各向同性的特點，不能根據不同的圖像結構進行自適應插值，導致插值后的邊緣部分出現如模糊、振鈴、鋸齒等明顯的人工處理痕跡。

以上基于線性回歸模型的插值算法雖然取得了較好的效果，但對邊緣兩側變化較劇烈的部分，其插值效果并沒有得到很好的改善。究其原因主要是在模型估計階段利用低分辨率像素估計的線性回歸模型參數，并不能完全適合高分辨圖像的結構，本文針對這一問題進行了改進。在模型參數估計階段，把低分辨率像素和已經估計的高分辨率像素作為訓練像素進行參數的估計，另外，引入了像素平滑方向作為正則化項，以降低插值窗口內結構的多變所帶來的插值誤差。

2 圖像自回歸模型

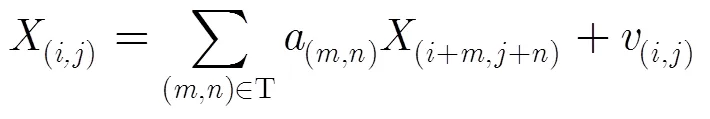
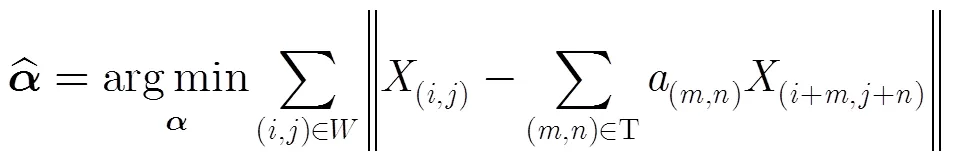
其中為固定大小的局部窗口。

3 本文算法

通常，在以未知像素為中心的局部窗口內進行參數估計后，就可以利用式(1)進行未知像素的插值，如圖1所示。實驗顯示，在平滑區域及兩側變化不大的邊緣這樣做會產生較好的插值效果。但對于兩側變化劇烈的邊緣而言，參數估計會因為圖像結構的多變導致誤估計，本文針對該問題進行了改進。首先在參數估計階段，將已知的低分辨率像素和已經估計出的高分辨率像素作為訓練像素，以降低由于分辨率不同而引起的參數估計誤差；在數據估計階段，首先估計出以待插值像素為中心的像素平滑方向，然后將利用平滑方向的像素估計出的像素值作為正則化項，以降低由于圖像結構多變導致的插值誤差。綜上所述，可用式(3)進行對未知像素的求解：

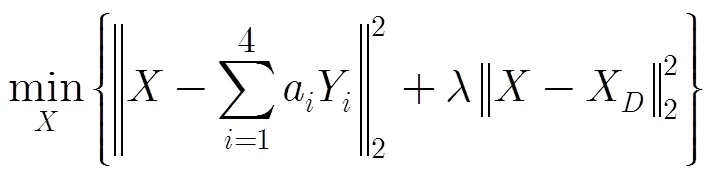
本文采用2遍插值對整幅圖像進行插值，如圖1所示，其中圖中黑色實心點為已知的低分辨率像素，白色點是第1遍插值操作的像素，灰色點是第2遍插值操作的像素。本文對邊界采樣用雙三次插值算法進行處理。下文以第1遍插值過程為例說明算法流程，算法流程圖如圖2所示。

圖1 基于線性回歸模型插值示意圖

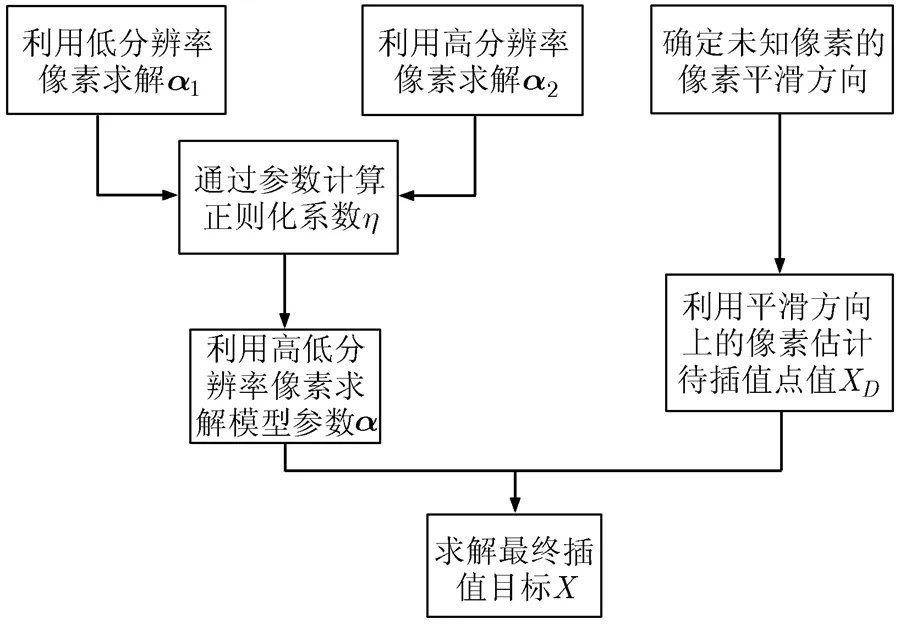
圖2 本文算法流程圖

3.1 模型參數估計

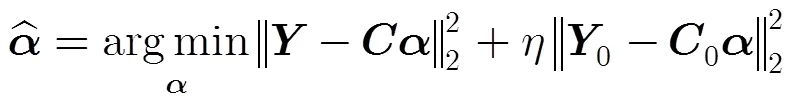
對式(4)進行求解得到

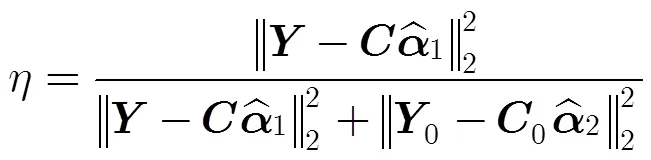
3.2 數據估計

在參數估計階段，假定插值窗口內的圖像結構都服從同一參數模型，然而對于兩側變化比較劇烈的邊緣來說，由于結構的多變不能很好地用同一參數模型進行描述，因而會產生較大誤差；為了克服圖像結構多變引起的邊緣插值不準確，本文引入了像素平滑方向作為正則化項，以使最終的插值結構更能適應圖像的局部結構。

4 實驗結果

為了評價本文算法的效果，本文選取了KODAK 圖像庫中的圖像作為測試圖像。首先對原始的高分辨率圖像進行以2為因子的隔點下采樣，將得到的對應的低分辨率圖像作為輸入圖像，然后用本文算法進行插值處理。同時將本文的插值效果與雙三次插值算法和RLLR插值算法進行了對比，對應的PSNR值如表1所示。

表1實驗重建結果衡量標準PSNR對比

雙三次插值算法RLLR插值算法[11]本文方法 Hats31.191031.273131.4767 Windows31.089531.237731.3359 Market22.179722.007122.2277 Sailboats30.181030.108330.3687 Sailboat30.179230.400730.5985 Lighthouse26.990926.816627.0447 Mustang29.280029.615729.7186 Average28.727328.779828.9673

對于彩色圖像，是將彩色圖像的3個通道當成3幅灰度圖像分別進行插值，最后將各通道的插值結果合并成彩色圖像。圖5是用3種算法對灰度圖像進行處理的實驗結果，圖6是用3種算法對彩色圖像處理的實驗結果。

從實驗結果可以看到，雙三次插值與RLLR插值算法在進行邊緣插值時，存在較嚴重的鋸齒和不平滑現象，如圖5中的白色線條和灰色線條，圖6中的白色直線處都出現了較明顯的鋸齒效應，本文算法能更好地保護圖像的邊緣部分。

圖5 灰度圖像插值結果

圖6 彩色圖像插值結果

5 結論

傳統的基于線性回歸模型的插值算法主要存在以下兩個問題：由于分辨率不同引入的參數估計誤差和由于局部圖像結構多變引入的數據估計誤差。針對這兩個問題本文提出了一種基于正則化的邊緣定向圖像插值算法。為了克服分辨率不同所引入的誤差，本文在參數估計階段，同時把低分辨率像素與已經估計的高分辨率像素作為訓練像素進行模型參數估計。在數據估計階段，通過引入像素平滑方向作為正則化項，用來克服圖像結構多變所帶來的誤差。實驗結果表明，本文算法取得了較好的視覺效果和較高的PSNR值，尤其在邊緣兩側變化劇烈的部分能更好地保護邊緣。

[1] Keys R C. Cubic convolution interpolation for digital image processing[J].,,, 1981, 29(6): 1153-1160.

[2] Hou H S and Andrews H C. Cubic splines for image interpolation and digital filtering[J].,,, 1978, 26(6): 508-517.

[3] Dong Wei-sheng, Zhang Lei, Shi Guang-ming,.. Nonlocal back-projection for adaptive image enlargement[C]. 16th IEEE International Conference on Image Processing (ICIP), Cairo, 2009: 349-352.

[4] Hung Kwok-wai and Siu Wan-chi. Single image super- resolution using iterative wiener filter[C]. IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, 2012: 1269-1272.

[5] Guo Kai, Yang Xiao-kang, Zha Hong-yuan,.. Multiscale semilocal interpolation with antialising[J]., 2012, 21(2): 615-625.

[6] 趙旦峰, 王博, 楊大偉. 一種邊緣定向平滑圖像插值算法[J]. 電子與信息學報, 2012, 34(7): 1543-1546.

Zhao Dan-feng, Wang Bo, and Yang Da-wei. An edge- directed smoothness algorithm for image interpolation[J].&, 2012, 34(7): 1543-1546.

[7] Zhang Lei and Wu Xiao-lin. An edge-guided image interpolation algorithm via directional filtering and data fusion[J]., 2006, 15(8): 2226-2238.

[8] Li Xin and Orchard M T. New edge-directed interpolation[J]., 2001, 10(10): 1521-1527.

[9] Asuni N and Giachetti A. Accuracy improvements and artifacts removal in edge based image interpolation[C]. Proceedings of the Third International Conference on Computer Vision Theory and Applications (VISAPP), Funchal, 2008: 58-65.

[10] Zhang Xiang-jun and Wu Xiao-lin. Image inerpolation by adaptive 2-D autoregressive modeling and soft-decision estimation[J]., 2008, 17(6): 887-896.

[11] Liu Xian-ming, Zhao De-bin, Xiong Rui-qin,.. Image interpolation via regularized local linear regression[J]., 2011, 20(12): 3455-3469.

[12] 任杰, 劉家瑛, 白蔚, 等. 基于隱式分段自回歸模型的圖像插值算法[J]. 軟件學報, 2012, 23(5): 1248-1259.

Ren Jie, Liu Jia-ying, Bai Wei,.. Image interpolation algorithm based on implicit piecewise autoregressive[J]., 2012, 23(5): 1248-1259.

[13] Hung Kwok-Wai and Siu Wan-Chi. Robust soft-decision interpolation using weighted least squares[J]., 2012, 21(3): 1061-1069.

[14] Tang K, Oscar C Au,and Fang Lu. Image interpolation using autoregressive model and gauss-seidel optimization[C]. 6th IEEE International Conference on Image and Graphics (ICIG), Hefei, China, 2011: 66-69.

[15] Tomasi C and Manduchi R. Bilateral filtering for gray and color images[C]. Proceedings of the Sixth International Conference on Computer Vision (ICCV), Bombay, 1988: 839-846.

季成濤： 男，1988年生，碩士生，研究方向為圖像處理、圖像超分辨率等.

何小海： 男，1964年生，教授，博士生導師，研究方向為圖像處理、數字通信等.

符耀慶： 男，1962年生，高級工程師，研究方向為計算機應用技術及圖像處理.

梁子飛： 男，1989年生，博士生，研究方向為圖像處理、圖像超分辨率等.

卿粼波： 男，1982年生，博士，講師，研究方向為圖像處理、圖像通信.

An Edge Directed Interpolation Algorithm Based on Regularization

Ji Cheng-tao①He Xiao-hai①Fu Yao-qing②Liang Zi-fei①Qing Lin-bo①

①(,,610065,)②(&,100027,)

The traditional methods based on linear regression model preserve the edge in some degree, but hardly work on the sharp edge. To solve this problem, an edge directed interpolation algorithm based on regularization is proposed in this paper, which is composed of the parameters estimation part and the data estimation part. In the first part, the high resolution structures which have been estimated are taken as one part of the training pixel to estimate the parameters of the linear regression model for effectively describing the structure. In the second part, the smooth pixel’s direction is applied as the regularization to reduce the error of estimated data aroused from the incorrect parameters. Experimented results show that the proposed method preserves the edge of image effectively, and both the visual effects and the PSNR are all better than bi-cubic and Regularized Local Linear Regression (RLLR).

Image processing; Interpolation; Regression model; Training pixel; Regularization

TN911.73

A

1009-5896(2014)02-0293-05

10.3724/SP.J.1146.2013.00582

何小海 hxh@scu.edu.cn

2013-04-25收到，2013-07-27改回

國家自然科學基金(61071161)，國家自然科學基金委員會和中國工程物理研究院聯合基金(11176018)資助課題