稀布圓陣的降維化方法

于 波 陳客松 朱 盼 王國強

?

稀布圓陣的降維化方法

于 波*①陳客松①朱 盼②王國強②

①(電子科技大學電子工程學院 成都 611731)②(中國民用航空總局第二研究所 成都 610041)

針對有陣列孔徑，陣元數目和最小陣元間距3種約束下的稀布圓形陣列綜合問題，該文提出了一種基于修正遺傳算法的降維優化方法。為了充分利用陣元布陣的自由度，同時使稀布陣列滿足多個設計約束，在陣元排布時將2維平面陣列優化設計降維成1維的稀布直線陣列，計算陣列性能時再還原為平面陣列。該方法改進了現有圓陣綜合方法中軌跡圓半徑和軌跡圓上陣元數分布優化的不足，實現了全部陣元的聯合優化，降低了算法的復雜性，同時保證了陣列的旁瓣性能，仿真結果證明了該方法的有效性。

稀布陣列；圓形陣列；旁瓣性能；遺傳算法；降維

1 引言

圓環陣列天線在很多應用中起著很重要的作用，例如聲吶、雷達、衛星通信系統等領域[1]。陣列天線的最大相對旁瓣電平(maxRSLL)是評價天線性能的一個重要參數，在給定陣列孔徑、陣元數目和最小陣元間距等約束條件的前提下，綜合出盡量低的旁瓣電平是陣列天線研究的重要課題之一[2,3]。近60年來，均勻間隔陣列的綜合已獲得了廣泛而深入的研究，在保持原始陣列的輻射特性下減少陣元數的研究已有很多方法，例如給定陣元數和陣列響應，可以利用傳統的道爾夫-切比雪夫綜合法、泰勒綜合法、傅里葉逆變換法和數值優化等方法實現陣列綜合；相對而言，非均勻陣列的綜合是尚未解決的難題。陣元間約束條件下的優化有兩種途徑，一種是陣元從相距半波長的規則柵格上稀疏的稀疏陣[4]；另一種是天線單元在設計時約束其陣元間距在一定孔徑范圍內隨機稀布的稀布陣[5]。近年來，為了得到峰值旁瓣性能良好的稀疏陣，已經出現了統計優化法、動態規劃法、遺傳算法[6,7]、模擬退火法、粒子群法[8]等綜合方法。

針對圓環上陣元數目和陣元分布位置不能聯合優化的問題，本文提出一種將屬于2維平面陣列的稀布同心圓環陣列(圓環半徑等間距)陣元分布優化設計降維成1維的稀布直線陣列陣元分布優化設計，建立2維同心圓環陣列與1維線陣的關系，基于修正遺傳算法進行線陣陣元位置的優化，獲得圓陣盡量低的峰值旁瓣電平，降低了優化的計算量和模型的復雜性，又對所有陣元進行了聯合優化，提高了陣列優化的自由度，在優化陣元分布位置的同時，也確定了各個圓環上的陣元數目。

2 稀布圓陣的多約束優化模型

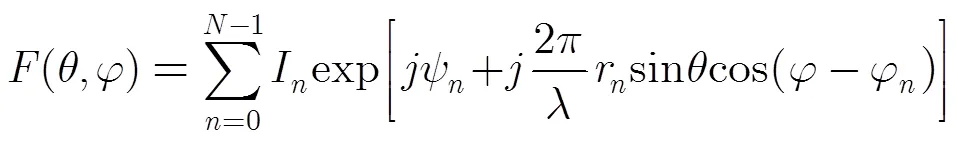
式中為工作波長，分別為波束方向的俯仰角和方位角。

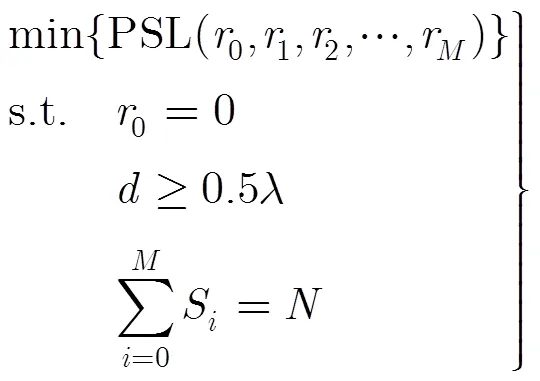
其中

3 圓陣陣元的降維排布方法

反之，如果已知某一陣元在直線陣列中的位置，則可以將其轉換為同心圓環陣列的極坐標位置。首先確定該陣元所在的圓環半徑，當圓環數滿足式(6)條件：

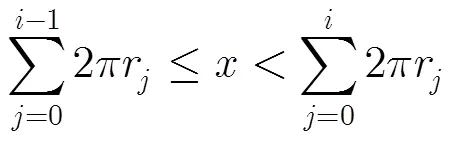
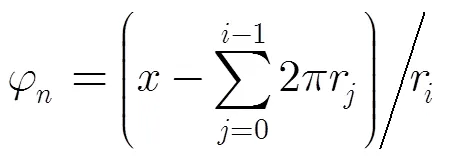
式(5)~式(7)就是圓環陣與線陣的相互轉化公式，本文討論的降維優化設計建立在這個基礎之上。針對具體的同心圓環陣的稀布優化設計，在轉化時還存在一些約束條件和近似處理。圓陣轉換為線陣后，同一圓環首尾陣元的最小間距約束問題，線陣轉換為圓陣后前一圓環末陣元與后一圓環首陣元間距約束的問題，下文會對此問題進行說明。

4 基于遺傳算法的優化算法

在遺傳算法中[15]，通常采用二進制碼優化變量，這種編碼方式非常適合交叉和變異操作，但是其搜索空間過大，運行性能較差，且存在二進制與十進制之間的轉換問題。實數編碼的遺傳算法以變量的真實十進制編碼代表變量的編碼方式，在克服二進制編碼缺點的同時，還具有更好的變異多樣性，反映真實的搜索空間，簡化計算量，從而提高了遺傳算法的效率和精度。文獻[16]提出了一種間接描述優化變量的修正遺傳算法(Modified Genetic Algorithms, MGA)來進行稀布陣列天線的優化設計。該算法回避了優化變量(陣元位置)的直接描述，并利用陣元的間距約束減小了遺傳算法的搜索空間。下面給出基于修正遺傳算法的稀布同心圓環陣列降維優化方法的主要步驟。

4.1 創立初始種群

4.2 交叉和變異

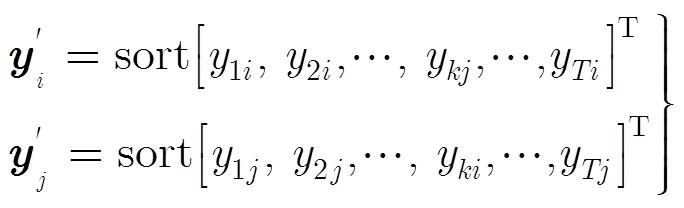
經過選擇、交叉和變異操作得到的新一代線陣種群為

4.3 適應度計算

將如式(11)所示的1維線陣上陣元的位置轉換在同心圓環陣列上的分布，相鄰兩個圓環的前一個圓環陣列上的末尾陣元與后一個圓環陣列上的起始

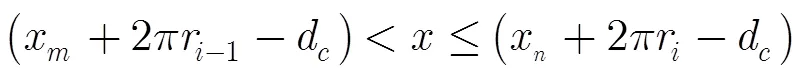
5 仿真結果

優化后的PSL為-23.74 dB，與均勻同心9圓環滿陣的PSL相比改善了6.34 dB；與文獻[11]中運用經典遺傳算法得到的最優稀疏同心9圓環陣列的PSL值-22.44 dB相比降低了1.30 dB；與文獻[11]中運用混合遺傳算法得到的半徑優化后的稀疏同心6圓環陣列的PSL值-22.94 dB相比降低了0.80 dB。本文方法用更少的陣元數獲得了更好的峰值旁瓣電平。

圖3 同心9圓環陣列

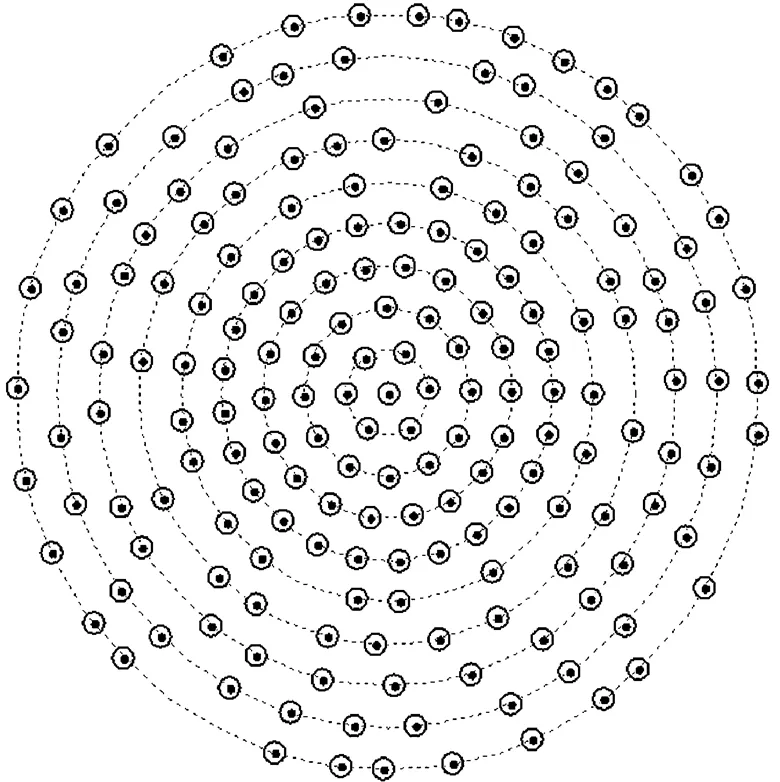
圖4 降維優化后的稀布陣列

上述同心9圓環陣列的對比結果如表1所示。仿真實驗在MATLAB7.10平臺中完成，計算機配置為：Pentium(R) Dual-Core E5200處理器，主頻2.5 GHz。從表中可以看出，修正遺傳算法的降維優化方法與經典遺傳算法相比，能在圓環上陣元數不確定的前提下，同時優化圓環上的陣元數目和陣元位置，實現了更好的旁瓣性能，同時，優化方法所需要的優化時間也明顯減少，實驗結果驗證了本文優化方法的有效性。

圖5 優化后的陣列方向圖

圖6 兩個截面的方向圖

表1同心9圓環陣列的優化結果對比

6 結束語

本文將降維處理運用于2維稀布陣列的陣元排布過程中，成功實現了多約束稀布圓形平面陣列綜合。借助修正遺傳算法將陣元在軌跡圓上的位置進行了統一的優化計算，完成了滿足多個設計約束的稀布圓陣優化。該方法不僅降低了平面陣列優化方法的復雜性，還為復雜陣列優化問題提供了有效的解決途徑，得到了旁瓣性能較優的稀布陣列。本文方法為解決此類陣列優化問題提供了有益的啟示，下一步我們將研究將該降維優化方法拓展到矩形口徑及橢圓形口徑的稀布平面陣列優化設計中。

[1] Singh U and Kamal T S. Synthesis of thinned planar concentric circular antenna arrays using biogeography-based optimization[J].&2012, 6(7): 822-829.

[2] Kumar B P and Branner G R. Generalized analytical technique for the synthesis of unequally spaced arrays with linear, planar, cylindrical or spherical geometry[J]., 2005, 53(2): 621-634.

[3] Zhang Wen-ji, Li Lian, and Li Fang. Reducing the number of elements in linear and planar antenna arrays with sparseness constrained optimization[J]., 2011, 59(8): 3106-3111.

[4] Eva R I and Oscar Q T. Thinned array synthesis including radiation pattern diversity in the elements[C]. Proceedings of the IEEE Electromagnetics in Advanced Applications (ICEAA), Torino, 2011: 853-856.

[5] Li Song-wen. Grate lobes/side lobes suppression for sparse array design by using genetic algorithms[C]. Proceedings of the IEEE Innovations in Bio-inspired Computing and Applications(IBICA), Shenzhen, 2011: 371-373.

[6] Haupt R L. Thinned arrays using genetic algorithms[J]., 1994, 42(7): 993-999.

[7] Mandal D, Majumdar A, Kar R,.. Thinned concentric circular array antennas synthesis using genetic algorithm[C]. Proceedings of the IEEE Research and Development (SCOReD), Putrajaya, 2011: 194-198.

[8] Mandal D, Kar R, and Ghoshal S P. Thinned concentric circular array antenna synthesis using particle swarm optimization with constriction factor and inertia weight approach[C]. Proceedings of the IEEE Recent Trends in Information Systems(ReTIS), Kolkata, 2011: 77-81.

[10] Reyna A and Panduro M A. Design of steerable concentric rings array using rotation properties and evolutionary optimization[C]. Proceedings of the IEEE Antennas and Propagation (EuCAP), Barcelona, 2010: 1-5.

[11] Haupt R L. Optimized element spacing for low sidelobe concentric ring array[J]., 2008, 56(1): 266-268.

[12] Sun Xue-jun, Gan Quan, and Tang Bin. Design of sparse concentric multi-circular array using micro-genetic optimum algorithm[C]. Proceedings of the IEEE Communications and Mobile Computing,Yunnan, 2009: 51-55.

[13] Pathak N N, Mahanti G K, and Singh S K. Synthesis of thinned planar circular array antennas using modified particle swarm optimization[J]., 2009, 12: 87-97.

[14] 薛正輝, 李偉明, 任伍. 陣列天線分析與綜合[M]. 北京: 北京航空航天大學出版社, 2011: 301-308.

[15] Whitley D. A genetic algorithm tutorial[J]., 1994, 4(2): 65-85.

[16] Chen Ke-song, He Zi-shu, and Han Chun-lin. A modified real GA for the sparse linear array synthesis with multiple constraints[J]., 2006, 54(7): 2169-2173.

于 波： 男，1985年生，碩士生，研究方向為稀布陣列天線及信號處理.

陳客松： 男，1973年生，副教授，研究方向為陣列天線、相控陣雷達及信號處理.

朱 盼： 男，1976年生，工程師，研究方向為計算機仿真、空管自動化.

An Optimum Method of Sparse Concentric Rings Array Based on Dimensionality Reduction

Yu Bo①Chen Ke-song①Zhu Pan②Wang Guo-qiang②

①(,,611731,)②(,610041,)

A dimensionality reduction method based on modified genetic algorithm is presented under the constraints of fixing the aperture, the number of elements and the minimum element spacing. In order to utilize effectively the freedom of array element, the proposed method transforms the positions of two-dimensional concentric rings array optimization design into one-dimensional linear array when sparse array meet multiple optimization constraints, and then restore to the concentric rings array when calculating its performance. The proposed method reduces greatly the computation time and the complexity of the model. Meanwhile, due to the combined optimization of all elements, the optimization design is improved. Simulation results demonstrate the effectiveness of the proposed method.

Sparse array; Concentric rings array; Side lobe level; Genetic algorithms; Dimensionality reduction

TN820.1+5

A

1009-5896(2014)02-0476-06

10.3724/SP.J.1146.2013.00526

于波 yubo1125@163.com

2013-04-19收到，2013-10-08改回

國家自然科學基金(U1233103)和中國博士后科學基金(2012M511919)資助課題