基于BDNM的橋梁結構可靠度預測

樊學平，呂大剛

(哈爾濱工業大學土木工程學院，150090 哈爾濱)

基于BDNM的橋梁結構可靠度預測

樊學平，呂大剛

(哈爾濱工業大學土木工程學院，150090 哈爾濱)

為了結合監測極值應力和應力參數(平均值)的先驗模型來對橋梁可靠度進行預測，認為極值應力隨時間變化的動態測量為一個時間序列，并考慮到貝葉斯動態線性模型(BDLM)的局限性，引入貝葉斯動態非線性模型(BDNM)對時變極值應力進行預測.運用BDNM建立了極值應力的狀態方程和監測方程，通過泰勒級數展開技術，將其近似轉化為貝葉斯動態線性模型(BDLM)，并通過貝葉斯因子來對應力信息進行監控，然后結合應力參數的先驗信息，對極值應力的狀態參數進行貝葉斯后驗概率推斷，建立動態模型對極值應力變化趨勢進行預測.基于監測信息，考慮到變量估計主觀認識的不確定性，引入折扣因子來確定狀態誤差方差.最后利用建立的BDNM和一次二階矩(FOSM)可靠度方法，對結構可靠度進行預測，并通過實例驗證了所建模型的合理性和適用性.

橋梁健康監測;應力;貝葉斯動態非線性模型;貝葉斯動態線性模型;可靠度預測

橋梁健康監測大致分為兩個階段［1-2］，第一個階段為健康監測系統的研制與開發，包括傳感器的研發和應用、數據無線傳輸系統的研發、數據采集與系統集成技術等，目前已處于成熟階段［3-4］;第二個階段為健康監測信息的應用，大量研究主要集中在模態參數識別、損傷識別、模型修正等領域［5］，而在橋梁結構的可靠度預測和評定方面，雖然已取得了一定成果［6-8］，但是基于橋梁結構的健康監測信息對結構的可靠度進行實時預測和評定，在國內外還處于研究起步階段.作為貝葉斯預測模型中最重要的一類模型，貝葉斯動態線性模型(BDLM)在大壩數據監測［9］、地基沉降數據預測［10］、混凝土結構性能預測［11-13］等領域已得到應用，但此模型在橋梁結構的健康監測領域還未得到廣泛應用.因而本文嘗試基于橋梁結構健康監測信息，建立基于監測極值應力的貝葉斯動態非線性模型，通過非線性函數的近似線性化［14-15］，將監測極值應力的貝葉斯動態非線性模型近似轉化為貝葉斯動態線性模型，然后基于建立的貝葉斯動態線性模型，對橋梁結構的可靠度進行離線實時預測，最后通過工程實例驗證所建模型的合理性.

1 橋梁監測極值應力的BDNM

健康監測系統在結構長期運營中，可采集大量數據信息，本文主要利用監測的極值應力信息，即監測系統每天采集的應力數據的極大值θt表示狀態變量，即監測應力極值的平均值(趨勢項數據);yt表示監測變量，即實時監測的應力極值.

1.1 BDNM的假定

文中建立的 BDNM假設:1)狀態變量(θt)的變化是馬爾科夫鏈［16］，且 θt與 θt-1呈非線性關系;2)觀測變量(yt)是相互獨立的，且yt只與狀態變量θt相關，yt與θt呈線性關系.

狀態變量與監測變量的遞推關系見圖1.

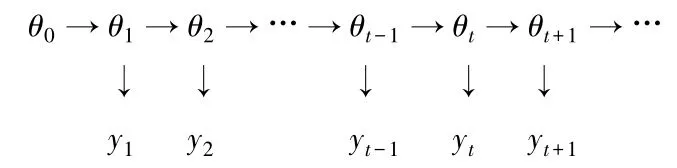
圖1 狀態空間模型的相關結構

1.2 BDNM的建立

貝葉斯動態模型主要由監測方程和狀態方程組成.由于橋梁健康監測信息的復雜性，本文采用每天的監測應力極值來反映結構的應力狀態.即主要通過建立監測應力極值的狀態方程和監測方程，實現監測應力極值的預測.

本文建立的橋梁監測應力極值非線性動態預測模型為

1)監測方程

2)狀態方程

3)初始先驗信息(t-1時刻的信息)

式中:yt為t時刻系統的監測應力極值;νt為監測誤差項;θt為t時刻的狀態變量(監測極值應力的平均值或趨勢項);ωt為狀態噪聲項;Vt和Wt分別為t時刻系統監測誤差和狀態噪聲的方差;gt(·)為狀態函數，且為非線性函數，它的物理意義是由應力極值隨時間的變化呈非線性變化，可以推出結構應力極值的狀態參數(極值應力的趨勢項數據或平均值)的變化亦呈現非線性［17］;Dt為t時刻以及t時刻以前的信息集，且Dt={yt，Dt-1}，Dt-1為t-1時刻以及t-1時刻以前的信息集，mt-1為t-1時刻狀態參數的平均值，Ct-1為t-1時刻狀態參數的方差;此外，假設 νt、ωt相互獨立，且都與.θt獨立.

2 BDNM到BDLM的轉化與遞推

2.1 非線性模型的線性化

根據橋梁的健康監測信息，擬合出監測極值應力信息的變化趨勢曲線h(t)(二次曲線)，此變化曲線近似作為狀態變量的變化曲線:

由于結構狀態變量的不可觀測性，即式(4)的非線性，因而本文把監測極值應力的趨勢曲線作為結構狀態變量的變化曲線.采用泰勒級數展開技術，可以將非線性狀態方程式(4)線性化為

式中h'(t)為h(t)在t時刻的斜率或一階差分.

將應力極值的貝葉斯動態非線性預測模型基于泰勒級數展開進行線性化，應力的變化趨勢一致，經本文作者研究變化所導致的相對誤差不超過5%，足以滿足實際工程的應用.由文獻［18］可知，監測應力極值可近似服從正態分布，因而可直接運用FOSM方法進行可靠度計算.

2.2 BDNM到BDLM的轉化

橋梁監測應力極值的近似動態線性模型為

1)監測方程

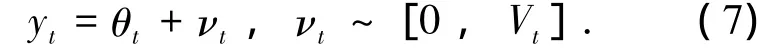
2)狀態方程

3)初始先驗信息

式中:h'(·)為狀態函數在信息集Dt-1上的變化率，mt-1、Ct-1可以通過信息集Dt-1近似統計得到.

本文模型時間間隔長度取為1 d，Vt根據監測應力極值信息的樣本方差進行估計;由文獻［11，19］可知 Wt=-Ct-1+Ct-1/δ，式中 δ為折扣因子，根據經驗一般取0.95 ～ 0.98.

2.3 BDLM的概率遞推

BDLM適用于正態分布的概率遞推，因而如果狀態變量服從非正態分布，那么首先要將狀態變量通過近似方法轉化為正態分布［11］，遞推過程如下:

1)t-1時刻的后驗分布

對于均值mt-1和方差Ct-1，有

2)t時刻的先驗分布

式中 at=mt-1，Rt=Ct-1+Wt.

3)t時刻一步預測分布

式中:ft=E(yt|Dt-1)=at，Qt=var(yt|Dt-1)=Rt+Vt，1/Qt為一步預測精度.

根據HPD區域的定義［14-15］，對于一步預測值的預測區間(95%的保證率)為

4)t時刻的后驗分布

2.4 動態模型擬合優度的檢驗

本文通過一步預測的方差和貝葉斯因子的變化曲線來對預測模型的擬合優度進行檢驗.

經過預測方差曲線可以得知預測精度的變化規律，而貝葉斯因子的變化規律可以體現動態模型實時預測精度的優劣.

具體檢驗準則如下:預測精度隨時間越來越大，則模型合理.

貝葉斯因子γ(t+1，t)反映了t+1時刻和t時刻模型對系統擬合的對比情況.若γ(t+1，t)≥1或者更大，則說明模型對于系統的擬合越來越好.

貝葉斯因子［14-15，20-21］的表達式為

式中:γ為動態貝葉斯因子;p(xt+1|Dt)為t時刻的一步預測概率密度函數在 xt+1處的值;p(xt|Dt-1)為t-1時刻的一步預測概率密度函數在xt處的值.

由于該因子的分子和分母都是監測應力極值的邊際密度，因此γ(t+1，t)反映了在t+1時刻和t時刻模型對系統擬合的對比情況.

3 橋梁結構的可靠度預測

3.1 一次二階矩方法(FOSM)

本文采用一次二階矩方法(FOSM)［22］預測橋梁結構或構件的可靠指標，即只考慮預測信息或監測應力極值信息的平均值和標準差.

假設隨機變量R(廣義抗力)和S(廣義荷載效應)相互獨立，其平均值和標準差分別為:μR，

廣義的極限狀態方程為

可靠指標按下式計算:

3.2 可靠度預測公式

本文所研究橋梁結構［20］的極限狀態方程為

式中:R為鋼材屈服強度，S為鋼材自重產生的應力，C為混凝土自重產生的應力，M為實時監測或預測的極值應力，γM為傳感器系數.

基于3.1節提到的FOSM，本文給出橋梁結構的可靠度預測公式為

式中:μM和σM分別為通過BDNM遞推得到的一步預測平均值與標準差;μR和σR分別為按照規范計算的抗力的均值和標準差;μS和σS分別為由鋼板恒載所引起的應力的均值和標準差;μC和σC分別為由混凝土恒載所引起的應力的均值和標準差;γP是傳感器的修正系數.

式(16)中的廣義抗力R的統計參數(μR，σR)對應式(18)的按規范計算所得的抗力的平均值和標準差(μR，σR);廣義荷載效應S的統計參數(μS，σS)包括三部分:1)鋼板恒載所引起的應力的均值和標準差;2)混凝土恒載所引起的應力的均值和標準差;3)貝葉斯動態模型遞推得到的活荷載效應的一步預測平均值與標準差.

4 實例驗證

某橋建于1961年，此橋為一座五跨連續鋼板梁橋［12，18，23-24］，全長 188.81 m，具體的橋梁工程資料及監測資料見參考文獻［18，23］.對第二跨跨中邊梁梁底的極值應力(CH15傳感器采集到的信號)進行了40 d的監測，結構可靠指標的閾值為4.2.日常監測極值數據見表1.

表1 實時監測極值數據(工作荷載造成的應力)

算例中鋼板梁橋的基本設計資料為

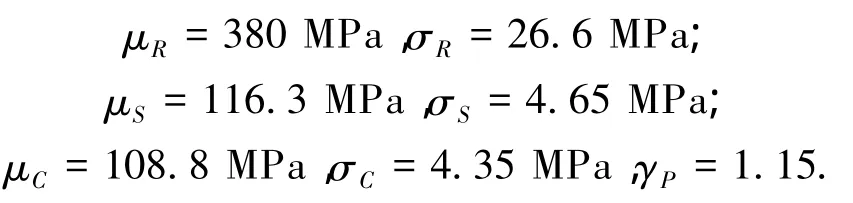
基于上述實時監測極值數據和基本設計資料，結合式(18)可得

4.1 擬合的應力變化趨勢曲線

為了得到監測信息的趨勢項數據信息，對監測極值數據進行曲線擬合和線性擬合;并經過擬合誤差分析，發現二次曲線擬合比線性擬合的精度高，因而本文采用二次擬合曲線近似作為監測極值的狀態曲線.

二次曲線擬合方程為

S(t)=-0.005 951t2+0.259 5t+23.48，狀態函數在信息集Dt-1上的變化率為

4.2 基于二次曲線擬合方程的動態線性模型

根據2.2節可得到近似的動態線性模型為

監測方程 yt=mt+ νt，νt～ N［0，V］;

狀態方程mt=mt-1+S't-1+ωt，

ωt～ N［0，Wt］;

先驗信息(mt-1|Dt-1)～f(x).

式中:yt為t時刻極值應力的監測數據;mt為t時刻極值應力的趨勢項值;S't-1為狀態函數在信息集Dt-1上的變化率;νt為監測誤差;ωt-1為狀態誤差，表示狀態的不確定性.V可由以前大量的監測信息來確定，且Wt=-Ct-1+Ct-1/δ(根據工程經驗取折扣因子為δ=0.98).

根據以前的監測應力極值資料以及設計資料可得狀態變量服從對數正態分布，即f(x)為對數正態分布，分布參數為:平均值μ=25.5 MPa，變異系數為0.186.基于上述動態線性模型計算所得的監測應力極值和可靠度預測結果以及預測精度見圖2～5.圖2表示的是預測曲線與實時監測曲線的對比，由圖2可知:監測應力的一步預測平均值的變化趨勢與實時監測應力的變化趨勢一樣.由圖3可知:隨著監測應力的不斷修正，一步預測精度越來越好.由圖4可知:隨著監測應力的修正，貝葉斯因子不斷地接近于1，說明動態模型的擬合優度較好.由圖5可知:隨著監測信息的修正，本文得到的可靠度指標比Frangopol［18］得到的可靠指標小，主要由于本文考慮了監測極值應力的不確定性或隨機性.

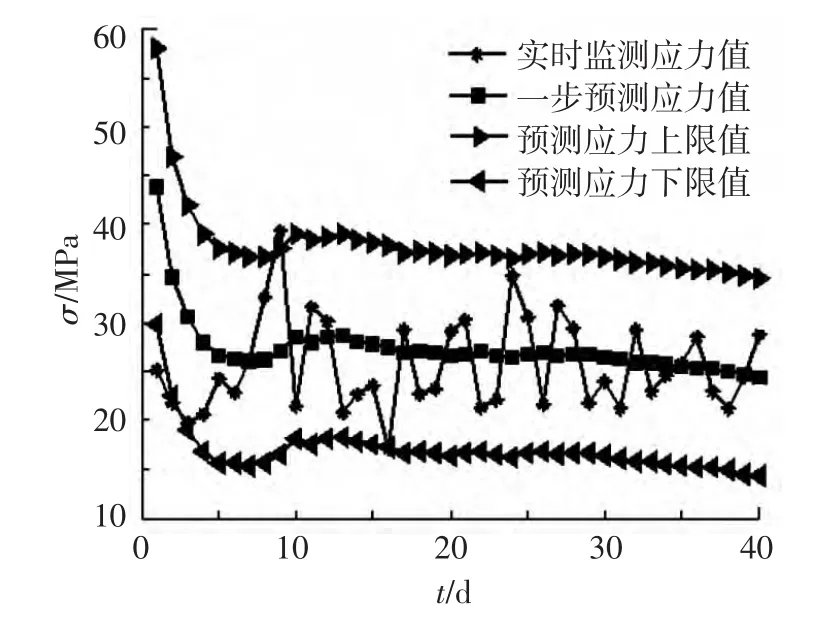
圖2 基于貝葉斯動態模型的監測應力極值預測曲線

圖3 預測精度的變化曲線

圖4 貝葉斯因子的變化曲線

圖5 可靠指標的變化曲線

5 結 論

1)建立了監測極值應力的貝葉斯動態非線性預測模型，并近似轉化為貝葉斯動態線性模型，經分析可得:一步預測方差越來越小，即預測精度越來越高.貝葉斯因子隨著時間的變化幾乎接近于1，說明建立的動態模型對系統的擬合較好.

2)對結構的可靠度進行了預測研究，相對于確定性(方差為0)的監測極值應力的可靠指標而言，本文考慮了監測應力的隨機性和不確定性，所得的可靠度較小，可以更好地對結構的安全狀態進行預測評定.

3)本文嘗試建立了少量離線監測數據的貝葉斯動態非線性模型，而基于較復雜的結構形式以及大量的的數據信息，建立合理的狀態方程和監測機制有待進一步研究.

［1］樊學平，呂大剛.基于多個BDLM的橋梁結構可靠度實時預測［J］.華南理工大學學報，2013，41(3):70-75.

［2］樊學平，呂大剛.基于貝葉斯動態模型和非均勻采樣的橋梁結構可靠度預測［C］//第22屆全國結構工程學術會議.烏魯木齊:新疆大學，2013:Ⅲ357-Ⅲ362.

［3］李惠，周文松，歐進萍，等.大型橋梁結構智能健康監測系統集成技術研究［J］.土木工程學報，2006，39(2):46-52.

［4］李愛群，繆長青，李兆霞，等.潤揚長江大橋結構健康監測系統研究［J］.東南大學學報，2003，33(5):544-548.

［5］秦權.橋梁結構的健康監測［J］.中國公路學報，2000，13(2):37-42.

［6］李星新，汪正興，王天亮，等.考慮目標可靠指標時變的既有橋梁動態可靠度評估［J］.橋梁建設，2007(增刊1):132-134.

［7］郭彤，李愛群，卞朝東.基于蒙特卡洛數值模擬的大跨橋梁狀態評估［J］.公路交通科技，2005，22(8):26-30.

［8］楊躍新.混凝土連續梁橋的時變可靠度評定與壽命預測［D］.哈爾濱:哈爾濱工業大學，2007.

［9］汪樹玉，劉國華，劉立軍，等.大壩監測分析中的貝葉斯動態模型［J］.水利學報，1998(7):1-5.

［10］魏冠軍，黨亞民，章傳銀.應用貝葉斯動態模型的地基沉降概率分析與預測［J］.測繪科學，2012，37(2):52-53.

［11］王劍.基于信息更新的混凝土結構性能預測和可靠性管理［D］.北京:清華大學，2006.

［12］樊學平.基于實時監測信息的混凝土連續梁橋時變可靠度評定［D］.哈爾濱:哈爾濱工業大學，2010.

［13］樊學平，呂大剛.基于DLM的橋梁結構承載力的貝葉斯預測［J］.哈爾濱工業大學學報，2012，44(12):13-17.

［14］WEST M，HARRISON P J.Bayesian forecasting and dynamic models［M］.2nd ed.New York:Springer-Verlag，1998.

［15］WEST M，HARRISON J.Bayesian forecasting and dynamic models［M］.New York:Springer Verlag，1989.

［16］嚴甜.基于MDP的橋梁結構全壽命成本研究［D］.哈爾濱:哈爾濱工業大學，2010.

［17］CATBAS F N，SUSOY M，FRANGOPOL D M.Structural health monitoring and reliability estimation:Long span truss bridge application with environmental monitoring data［J］.Engineering Structures，2008，30:2347-2359.

［18］FRANGOPOL D M，STRAUSS A，KIM S.Use of monitoring extreme data for the performance prediction of structures:general approach ［J］. Engineering Structures，2008，30:3644-3653.

［19］GAO L F，LIU F S.The monitoring of Bayesian dynamic linear models without normal assumptions［J］.Journal of Mathematics，2005，25(3):245-248.

［20］蘇兵.貝葉斯動態模型的模擬處理［D］.濟南:山東大學，2007.

［21］PETRIS G，PETRONE S，CAMPAGNOLI P.Dynamic linear models with R［M］.New York:Springer Series，2009.

［22］MELCHERS R E.Structural reliability analysis and prediction［M］.2nd ed.Chichester:John Wiley ＆ Sons，1999.

［23］MAHMOUD H N，CONNOR R J，BOWMAN C A.Results of the fatigue evaluation and field monitoring of the I-39 Northbound Bridge over the Wisconsin River［R］.ATLSS report no.05-04.Bethlehem:Lehigh University，2005.

［24］STRAUSS A，FRANGOPOL D M，KIM S.Use of monitoring extreme data for the performance prediction of structures:Bayesian updating ［J］. Engineering Structures，2008，30:3654-3666.

Reliability prediction of bridge structures based on BDNM

FAN Xueping，Lü Dagang
(School of Civil Engineering，Harbin Institute of Technology，150090 Harbin，China)

To predict the bridge structural reliability based on the monitoring information and the priori model of stress parameters(mean)，the dynamic measure of structural stress over time is treated as a time series，and considering the limitation of the BDLM，a Bayesian dynamic nonlinear model(BDNM)is then introduced.State equation and monitoring equation of monitoring stress are established with BDNM.Then the BDNM is approximately transferred into Bayesian dynamic linear model(BDLM)by Taylor series expansion technique，and the monitoring information is monitored by bayes factor.Combining parameters’ prior information with the early stress data containing noise，the stress state parameters are deduced with Bayesian Posterior Probability.A dynamic model is built to forecast the changing trend of structural stress.To allow for the epistemic uncertainty in variance estimation based on monitoring information，a discount factor approach is made for specification of unknown variance.Finally based on the built BDNM and the FOSM method，the structural reliability is predicted，and the feasibility and application of the built model is illustrated by an actual example.

bridge structural health monitoring;stress;BDNM;BDLM;reliability prediction

TU391;TU392.5

A

0367-6234(2014)02-0001-05

2013-03-04.

國家自然科學基金資助項目(50678057).

樊學平(1985—)，男，博士研究生;

呂大剛(1970—)，男，教授，博士生導師.

呂大剛，ludagang@hit.edu.cn.

(編輯 趙麗瑩)