現澆板對空間框架結構抗震性能影響

寧 寧，屈文俊，朱 鵬

(同濟大學土木工程學院建筑工程系，200092 上海)

現澆板對空間框架結構抗震性能影響

寧 寧，屈文俊，朱 鵬

(同濟大學土木工程學院建筑工程系，200092 上海)

為研究現澆板對框架結構抗震性能的影響，以現澆板的作用為主要研究內容，開展了兩個空間框架模型的水平低周反復抗震試驗.通過試驗數據對空間框架結構的破壞形態、承載力、剛度退化過程、滯回特性、變形特點以及耗能能力等抗震性能進行分析.結果表明:現澆板使框架承載力提高而變形能力降低;模型耗能能力變化不大.模型破壞時由“強柱弱梁”破壞機制向“強梁弱柱”破壞機制轉變;且由于板的空間作用使承載力退化速度降低而剛度退化加快.模型整體抗震性能良好.

現澆板作用;鋼筋混凝土空間框架;抗震性能

實際框架結構的抗震性能、破壞過程和受力機制與不考慮現澆板作用的空框架有差異.目前，國內外對框架結構的抗震性能試驗研究未能充分考慮現澆板的影響［1－5］.為研究現澆板對框架結構抗震性能的作用，國內外學者開展了一系列試驗與理論研究［6－10］.其中，Franco 等［6］進行了帶現澆板邊節點的擬靜力對比試驗，Zerbe等［7］對帶現澆板的邊節點、中節點以及平面框架進行了試驗研究.研究結果表明:現澆板對框架的抗震性能有一定影響，并建議了現澆板有效翼緣寬度的取值范圍.但以上研究均未考慮結構的空間作用.本文基于兩個1∶2.5的空間縮尺框架的低周反復試驗，對比了帶現澆板與不帶現澆板空間框架的承載能力、剛度退化、延性、變形能力、破壞模式和滯回耗能等抗震性能.

1 試驗設計

1.1 試驗材料

試驗采用PO42.5普通硅酸鹽水泥，JC－3型緩凝高效減水劑，砂為普通中砂，天然粗骨料為碎石，連續級配，拌合水為自來水.模型分兩批次澆筑，一層與二層混凝土澆筑后28 d力學性能見表1.柱縱向受力鋼筋采用HRB335級鋼筋，梁、板受力鋼筋與箍筋采用HPB235級鋼筋，其中柱鋼筋直徑為10 mm，梁鋼筋直徑為8 mm，現澆板鋼筋及箍筋直徑為6 mm，實測鋼筋的屈服強度、極限強度與彈性模量見表2.

表1 混凝土力學性能

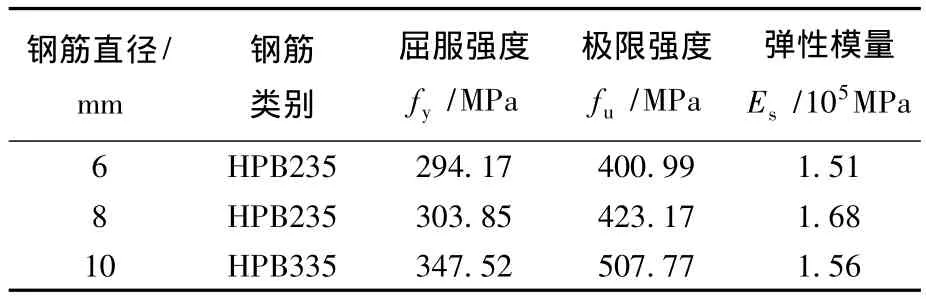
表2 鋼筋力學性能

1.2 模型設計

本次試驗共計兩個模型:未設現澆板的空間框架KJ－1與有現澆板空間框架 KJ－2.模型依據GB50011—2008《建筑抗震設計規范》［11］規定，按照8度二級框架結構進行配筋和構造設計，模型一層長跨角柱、短跨角柱和邊柱的實際軸壓比分別為0.007、0.006 和 0.012;二層分別為 0.003 5、0.003和0.006.兩個模型尺寸相同，均采用2跨×1跨“日”字形兩層空間框架結構.模型長4 m，寬1.6 m，高2.88 m.長邊方向長跨為2.4 m，短跨1.6 m;短邊方向橫跨1.6 m.柱尺寸 160 mm×160 mm，梁尺寸100 mm×200 mm，現澆板厚50 mm，基礎底座尺寸300 mm×400 mm.模型尺寸及配筋見圖1.

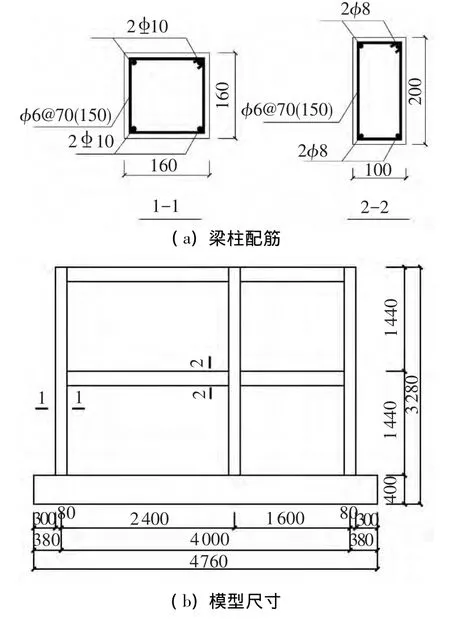
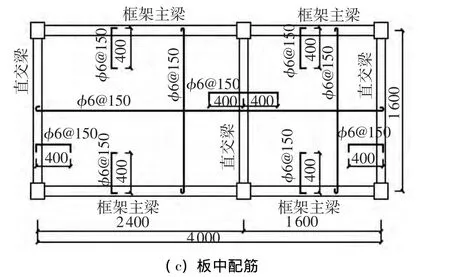
圖1 模型尺寸和配筋

1.3 試驗方法和加載制度

試驗在同濟大學建筑結構試驗室進行.參考JG101—96《建筑抗震試驗方法規程》規定，本次試驗采用擬靜力試驗方案.為防止模型發生平面外扭轉，采用兩個油壓千斤頂在框架頂層同步施加水平低周反復荷載，加載見圖2.為保證KJ－1和KJ－2質量相同，試驗前在KJ－1各個梁上堆載以模擬施加現澆板重量.

圖2 模型加載裝置

試驗采用位移控制加載，正式試驗前采用±2 mm(0.05%位移角)預加載，以測試應變片等儀器是否正常工作.

正式試驗時位移由±3 mm(0.1%)—±6 mm(0.2%)—±9 mm(0.3%)—±12 mm(0.4%)—±17 mm(0.6%)—±23 mm(0.8%)—±29 mm(1%)—±36 mm(1.25%)—±43 mm(1.5%)—±58 mm(2%)—± 72 mm(2.5%)—± 86 mm(3%)—±101 mm(3.5%)—±110 mm(4%)—±120 mm(4.2%)，每級位移循環3次.試驗過程中加卸載速度保持勻速.

1.4 測點布置和量測內容

試驗采用YHD型位移計.為量測模型平面內外側移大小、梁柱轉角和直交梁扭轉，KJ－1共布置13個位移計，KJ－2共布置17個位移計，其中在基礎底座的位置布置位移計，用于測量底部滑移.

用于量測梁、柱及板中鋼筋等應變變化情況的電阻應變片規格為B×120－5AA，格柵為50×3.混凝土應變片規格B×120－50AA，用以量測現澆板混凝土應變變化情況.

2 試驗結果與分析

2.1 破壞形態和破壞機制

1)破壞形態.KJ－1模型在加載初期(±3 mm)未出現開裂現象，隨著加載進行，當達到±6 mm時，一層在短跨角柱柱腳和各個梁端受拉區混凝土開裂，裂縫寬度約為0.2 mm.此時，模型滯回曲線包圍面積狹小，模型基本上處于彈性工作階段.隨著水平位移的不斷增加，梁、柱端混凝土不斷出現新裂縫，裂縫寬度逐漸增大，開裂現象明顯.當達到1.5%～2%(43～58 mm)層間位移角時，裂縫基本出齊，并不斷擴大.±58 mm時可聽到較清晰混凝土破碎聲音，一層邊節點節點核心區出現斜裂縫.當到達加載階段末期時，一層角節點混凝土保護層脫落，柱腳混凝土受壓破壞，鋼筋屈服(圖3).KJ－1模型一層各個梁端鋼筋全部屈服，混凝土開裂較大(圖4)，呈明顯的“強柱弱梁”破壞機制.

KJ－2模型在試驗初期時混凝土的開裂、擴展過程與KJ－1模型相似，但梁端裂縫明顯減少，柱端裂縫明顯增多，且現澆板中出現平行于短跨方向的細裂縫與斜裂縫.隨著加載進行，當達到±43 mm～±58 mm時，梁、柱裂縫基本出齊，節點核心區同時出現斜裂縫.±58 mm時可聽到較清晰混凝土破碎聲音，梁柱裂縫加寬，隨后現澆板已有裂縫加寬并不斷出現新裂縫(圖5).由于現澆板鋼筋受拉，使得直交梁梁端扭轉裂縫明顯(圖6).最終，模型一層柱腳混凝土受壓豎向開裂，鋼筋屈服，一層角節點側面混凝土保護層脫落.對比KJ－1與KJ－2模型的最終破壞形態，KJ－2最終破壞時二層邊柱底部鋼筋屈服，混凝土開裂較大，且邊節點兩側梁端裂縫較KJ－1 少.KJ－1 與KJ－2 混凝土裂縫分布情況見圖7.

兩框架加載全過程，平面外位移計讀數均很小，表明框架扭轉現象不明顯，可忽略.

圖3 柱腳混凝土破壞形態

圖4 梁端塑性鉸

圖5 現澆板裂縫

圖6 KJ－2直交梁扭轉裂縫

2)破壞機制.KJ－1、KJ－2的塑性鉸位置見圖8.對比兩個模型的最終破壞形態，KJ－1的破壞形態為“強柱弱梁”模式，塑性鉸首先在梁端出現，最后形成梁鉸機制破壞，但是柱腳破壞是不可避免的，而且一旦柱腳塑性鉸出現，其發展比梁鉸快.有現澆板的KJ－2柱端塑性鉸明顯增多，其中一層的兩根柱出現了兩端塑性鉸的破壞形態.說明由于現澆板的存在，使整個結構由“強柱弱梁”破壞機制轉向“強梁弱柱”的破壞機制.二層柱頂破壞嚴重，而頂層梁端鋼筋屈服和塑性鉸出現與發展比較遲緩，這主要是由于水平加載裝置使柱頂形成局部應力集中造成的［1］.

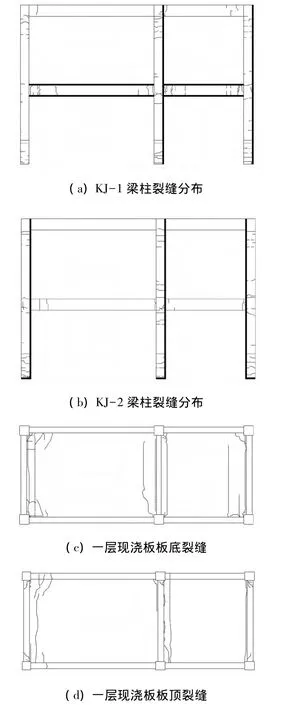
圖7 裂縫分布

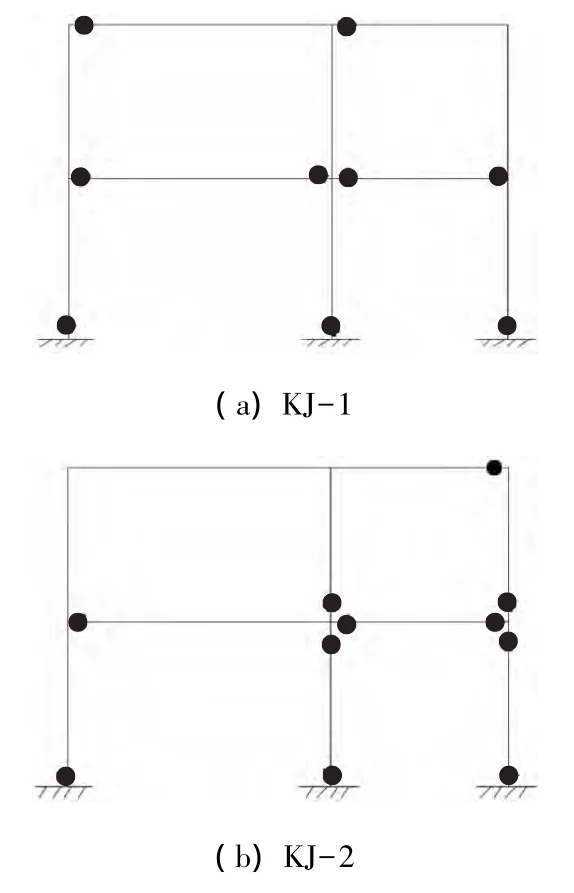
圖8 塑性鉸位置

2.2 滯回耗能能力

滯回曲線反映了在低周反復試驗中，水平作用力與側移之間關系曲線.它是進行抗震設計的重要依據.KJ－1、KJ－2在低周反復荷載作用下的P－Δ滯回曲線見圖9、10.

1)在試驗加載初期(±6 mm)，模型滯回環包圍面積狹小，力和位移基本上呈直線變化.剛度退化不明顯，結構的耗能較低.

2)結構進入彈塑性階段后，滯回曲線呈弓形，曲線趨向豐滿，耗能能力加強.對比現澆板作用對滯回曲線的影響:兩框架滯回曲線的形狀基本相似;KJ－2滯回環所包圍面積較KJ－1增大，表明KJ－2較KJ－1耗能增大.

3)隨著循環次數的加大，模型耗能能力不斷增強，在每一級位移階段，后一次循環都較前一次的荷載低，說明剛度和強度由于損傷累積的影響而不斷下降.

圖9 KJ－1的滯回曲線

圖10 KJ－2的滯回曲線

2.3 骨架曲線

KJ－1與KJ－2的骨架曲線見圖11.

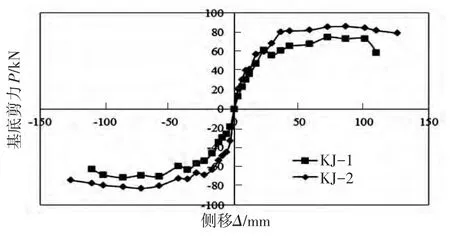
圖11 框架骨架線

1)在低周反復荷載作用下，KJ－1與KJ－2骨架線上均有明顯的開裂點，屈服點、最大荷載點和極限位移點;模型經歷了彈性、彈塑性和極限破壞三個階段.

2)對比現澆板作用對兩框架骨架線的影響，KJ－1與KJ－2骨架曲線形狀基本相同，KJ－2的承載力明顯高于KJ－1，且峰值點后KJ－2的強度降低速度較KJ－1緩和.

從骨架曲線可得出，由于KJ－2的基底剪力較KJ－1提高，在層間側移角2%(58 mm)時，KJ－2的基底剪力是KJ－1的1.14倍.基底剪力的增大使一層各柱剪力增大，從而導致柱端彎矩的增大，使KJ－2底層柱端更容易出現塑性鉸.建議設計中增大底層柱配筋，保證實現“強柱弱梁”破壞機制.

2.4 特征荷載與特征位移

模型的屈服荷載Py與峰值荷載Pmax見表3.其中模型屈服荷載的大小按能量等值法來確定.KJ－2的屈服荷載較KJ－1提高13.7%，峰值荷載提高15.2%.表明現澆板的存在較明顯地提高了框架承載力.

模型屈服位移Δy和峰值位移Δmax(峰值荷載對應的位移)見表3.KJ－2的屈服位移較KJ－1降低16.7%，峰值位移KJ－2較KJ－1降低2.2%.采用位移延性系數μ=Δmax/Δy與極限位移角Rmax=Δmax/H來反映結構延性的大小 (H為模型高度).計算結果表明，兩框架均具有良好延性;兩框架的極限位移角分別為1/35和1/36，說明KJ－1的變形能力略優于KJ－2，兩框架均具有良好的變形能力.

表3 特征位移與特征荷載

2.5 剛度退化曲線

在低周反復抗震試驗中，當模型屈服以后，隨著側移增加，模型剛度也逐步降低.為了考察框架在低周反復荷載作用下的剛度退化情況，本文采用每級加載過程中，第一次循環所對應的割線剛度來表示模型剛度退化特性.KJ－1、KJ－2剛度退化曲線見圖12.

對比兩框架剛度退化曲線，KJ－2初始剛度較KJ－1增大74.6%(正向)與119.2%(負向)，說明現澆板的存在增大了結構整體剛度.模型剛度隨側移增加而降低，其退化趨勢基本接近，當達到試驗加載末期，兩框架剛度基本相同.

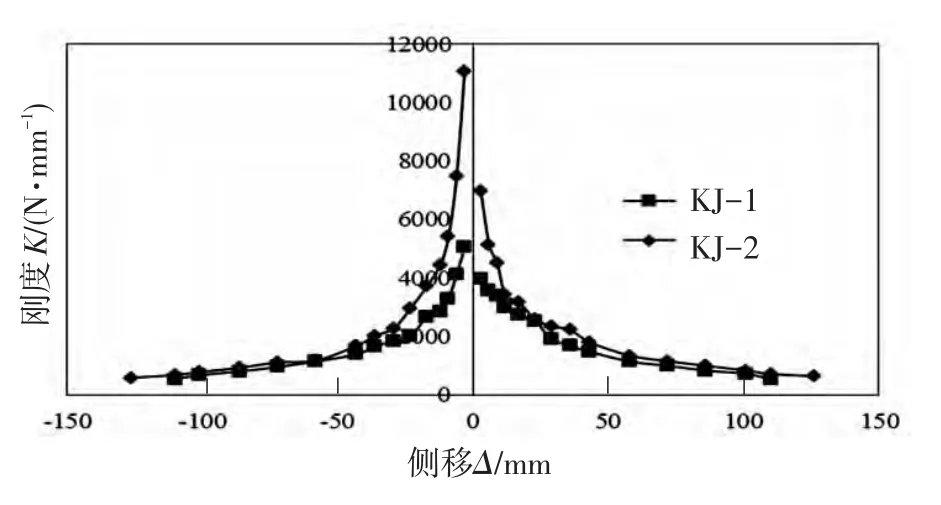
圖12 剛度退化曲線

2.6 耗能能力

評價結構的滯回耗能能力一般采用荷載 －位移曲線包絡的圖形面積來衡量，滯回曲線包絡線越飽滿，則模型的耗能能力越強，其抗震性能越好.現代工程抗震中，采用等效粘滯阻尼比he來判斷構件的耗能能力.

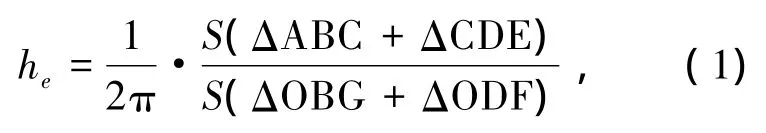
式中:S(ΔABC+ ΔCDE)、S(ΔOBG+ ΔODF)對應的面積見圖13.

按式(1)計算兩框架在不同側移下的he變化趨勢見圖14.模型在加載初期，he都較低，隨著側移不斷增加，he呈非線性遞增.最終，he均超出0.2，表明鋼筋混凝土框架結構具有良好的滯回耗能能力.對比現澆板對耗能能力的影響，兩框架的he相差不大，考慮現澆板作用對結構整體滯回耗能影響不大.

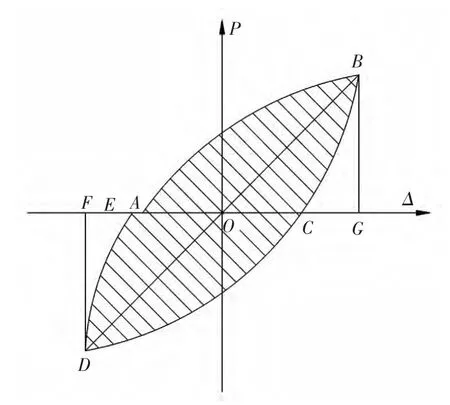
圖13 耗能能力定義

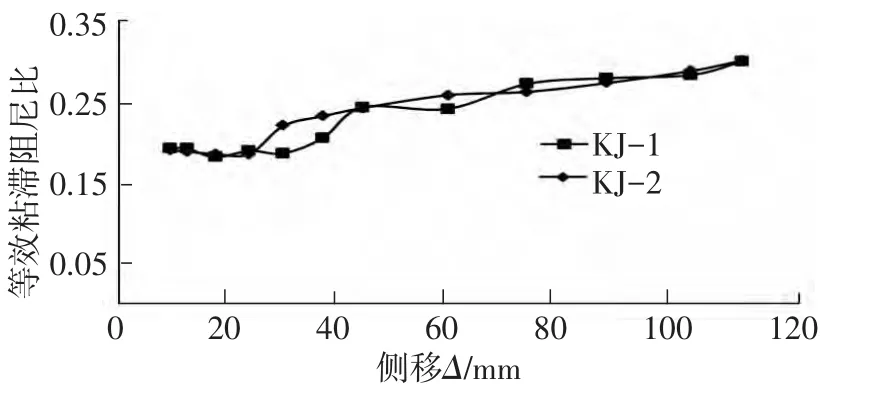
圖14 等效粘滯阻尼比

2.7 側移曲線

通過布置在每層的位移計測得數據，對比KJ－1、KJ－2在 0.1%，1%和 2%位移角下的整體側移曲線見圖15.模型沿豎向的側移具有很好的連續性;兩個模型側移曲線的形狀基本相同，現澆板對框架側移曲線的形狀影響不大.

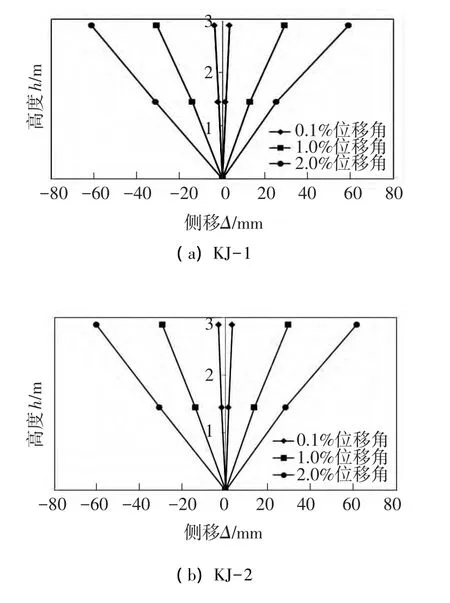
圖15 側移曲線

對比模型在2%位移角下一層與二層層間位移的大小:其中 KJ－1一層平均層間位移為28.2 mm，二層平均層間位移為31.9 mm;KJ－2一層層間位移為 29.5 mm，二層層間位移為32.4 mm;其層間位移角均滿足規范關于框架結構彈塑性層間位移角限值1/50［11］的規定.

3 結 論

1)現澆板對框架破壞機制有一定影響，KJ－1為梁鉸破壞機制;KJ－2轉為梁柱混合鉸破壞機制，且一層部位兩根柱端均出現塑性鉸;由于現澆板的存在，KJ－2直交梁發生扭轉，扭轉裂縫集中在約一倍梁高范圍.

2)現澆板的存在改善了模型的整體性能與承載力，KJ－2峰值荷載較 KJ－1有明顯提高.KJ－2滯回曲線與KJ－1相似，但滯回環包絡面積增大.

3)現澆板對模型剛度有明顯影響，KJ－2的初始剛度較KJ－1有較大提高，但二者剛度退化趨勢相似，且接近破壞時，二者剛度相差不大.

4)現澆板的存在降低了結構的變形能力，KJ－2變形系數小于KJ－1.對比現澆板對模型耗能能力的影響，兩框架相差不大，均有良好耗能能力.

5)兩個模型側移曲線的形狀基本相同，現澆板對框架側移曲線的形狀影響不大.

6)在抗震設計中，宜增大底層柱配筋，建議在規范規定的基礎上增大15%;同時應考慮現澆板受拉有效翼緣寬度范圍內的板筋參與梁端受彎，并將柱端彎矩增大系數η值提高20%，以確保形成“強柱弱梁”破壞機制.

7)影響框架結構“強柱弱梁”的其他因素如填充墻、軸壓比等仍有待進一步研究.

［1］徐云扉，胡慶昌，陳玉峰，等.低周反復荷載下兩跨三層鋼筋混凝土框架受力性能的試驗研究［J］.建筑結構學報，1986(2):1－12.

［2］肖建莊，黃鈺，李杰，等.兩層半子結構框架試驗方法研究［J］.地震工程與工程震動，2002，22(1):73－78.

［3］鐘益村，任富棟，田家燁.二層雙跨鋼筋混凝土框架彈塑性性能試驗研究［J］.建筑結構學報，1981，(3):34－41.

［4］印文鐸，馮世平，沈聚敏.兩層鋼筋混凝土框架結構擬動力地震反應試驗研究［J］.土木工程學報，1990，23(3):23－35.

［5］薛偉辰，胡翔.四層兩跨高性能混凝土框架的抗震性能［J］.建筑結構學報，2007，28(5):69－79.

［6］DI FRANCO M A，MITCHELL D，PAULTRE P.Role of spandrel beam on response of slab-beam-column connections［J］.Journal of Structural Engineering，1995，121(3):408－419.

［7］ZERBE H E，DURRANI A J.Seismic response of connections in two-bay reinforced concrete frame subassemblies with a floor slab［J］.ACI Structural Journal，1990，87(4):406－415.

［8］QI X，PANTAZOPOULOU S J.Response of RC frame under lateral loads［J］. Journal of Structural Engineering，1990，117(4):1167－1188.

［9］AMMERMAN O V，FRENCH C W.R/C beam-columnslab subassenblages subjected to lateral loads［J］.Journal of Structural Engineering，1989，115(6):1289－1308.

［10］FRENCH C W，BOROOJERDI A.Contribution of R/C floor slabs in resisting lateral loads［J］.Journal of Structural Engineering，1989，115(1):1－18.

［11］GB 50011—2001建筑抗震設計規范［S］.北京:中國建筑工業出版社，2008.

Effect of cast in-situ slabs on seismic performance of spatial RC frames

NING Ning，QU Wenjun，ZHU Peng
(Department of Building Engineering，College of Civil Engineering，Tongji University，200092 Shanghai，China)

To study the affection of cast in-situ slabs in RC frames during earthquakes，this paper presents a low cyclic loading test for two spatial RC frames.The failure pattern，loading carrying capacity，stiffness degradation，deformation characteristic and energy dissipation capacity are experimentally studied.Research findings indicate that the loading carrying capacity of the frame with cast in-situ slabs increase and the deformation capacity decrease.However，the energy dissipation capacity changes slightly.The failure patterns of the frame with cast in-situ slabs changes from“strong column weak beam failure”to the“strong beam weak column”.The degradation of loading carrying capacity decreases and the stiffness degradation increases due to the effect of slabs.All the frames exhibit good seismic performance.

cast in-situ slabs;spatial RC frames;seismic performance

TU375.3

A

0367－6234(2014)02－0072－06

2013－03－27.

國家科技支撐計劃(十一五)項目(2006BAJ03A07－04).

寧 寧(1982—)，女，博士研究生;

屈文俊(1958—)，男，教授，博士生導師.

屈文俊，quwenjun.tj@tongji.edu.cn.

(編輯 趙麗瑩)