慣性矩二次變化變截面梁柱幾何非線性分析
孟麗霞,陸念力,劉士明
(哈爾濱工業大學機電工程學院,150001 哈爾濱)
慣性矩二次變化變截面梁柱幾何非線性分析
孟麗霞,陸念力,劉士明
(哈爾濱工業大學機電工程學院,150001 哈爾濱)
為研究考慮剪切變形的變截面梁桿結構幾何非線性問題,應用Timoshenko梁理論,采用位移、轉角獨立插值的方法,獲取考慮剪切影響的慣性矩二次變化變截面梁單元的形函數;從嚴格的虛功增量方程出發,建立同時考慮軸力、剪切、彎曲效應及其耦合項的平面變截面梁柱單元幾何非線性增量平衡方程,得到慣性矩二次變化變截面梁單元大位移切線剛度陣;與經典算例進行對比,驗證了本文方法的精確性與有效性.
有限單元法;變截面梁;虛功增量方程;大位移;幾何非線性
梁桿結構由于自重輕、承載能力大等優點而在工程中得到廣泛應用.隨著優質鋼材等級的提高,梁桿結構跨度與柔度不斷增大,梁桿結構的受載形式表現為強非線性,此時傳統的小位移假定已不再適用.在幾何非線性分析方面,1975年,文獻[1]提出了非線性增量形式的完全拉格朗日(T.L.)和修正拉格朗日(U.L.)描述.文獻[2]改進了 Bathe的方法,通過建立三維連續梁的虛功增量方程,推導了分析三維梁式構件大撓度問題的U.L.列式法,并提出了新形式的梁單元之幾何剛度陣.文獻[3]通過建立考慮剪切變形與彎曲變形影響的修正剪切方程,對半剛性連接的單根梁柱的大位移大轉動小應變問題進行分析研究.文獻[4]使用C.R法分析了薄壁梁的大位移幾何非線性問題.但上述研究對象均為等截面梁,對于變截面梁單元,文獻[5]在獲得小位移Euler-Bernoulli變截面梁單元剛度陣基礎上,利用隨動坐標法,在變形后位形上建立單元隨動坐標系,得到變截面梁單元大位移全量平衡方程,所得剛度陣并未計及剪切變形的影響.文獻[6]基于修正的拉格朗日列式法,采用等截面Timoshenko梁單元形函數代入虛功方程,給出了可直接用于幾何非線性分析的變截面梁單元彈性和幾何剛度矩陣.以往研究中,要么對變截面梁單元形函數簡單采用等截面形函數代替[6],并未考慮剪切變形與變截面因素的影響,要么在虛功方程中忽略了單元軸向變形與剪切變形及各耦合項對結構的影響[7~8].
本文利用多項式插值,采取轉角與位移獨立插值的方法構造計及剪切與變截面因素的位移場,隨后運用更新的拉格朗日列式法建立嚴格的平面梁柱單元的大位移虛功增量方程,得到包括各種耦合項的慣性矩二次變化變截面梁單元大位移切線剛度陣.最終得到顯示表達的變截面梁單元大位移線性剛度陣與幾何剛度陣.
1 慣性矩二次變化變截面梁單元
變截面梁單元以其受力合理以及節約材料等特點而得到廣泛應用.工程中,等效為慣性矩二次變化的變截面梁多見于格構式結構與腹板鏤空的工字梁.如圖1所示慣性矩二次變化的變截面梁,構件截面面積為定值A0,構件長度為L,在x=0處的截面慣性矩為I1,在x=L處的截面慣性矩為I2,則任意截面x處的截面慣性矩可表示為坐標x的函數:
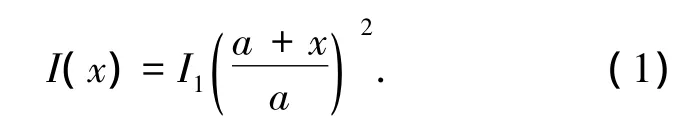
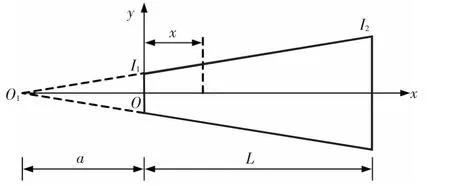
圖1 平面變截面梁單元
在單元局部坐標系下,推導變截面梁單元切線剛度矩陣過程中使用如下基本假定:
1)梁單元變形后的截面形狀保持不變,即為剛性截面;2)梁單元受載形式為大位移小應變情況;3)垂直于中面的截面變形后仍保持為平面,但不必再與變形后的中面垂直;4)單元材料為各向同性線彈性材料,遵循廣義虎克定律;5)構件截面特性沿軸向連續變化,且構件為雙軸對稱.則構件的橫截面面積及截面慣性矩可表示為軸向坐標的函數形式
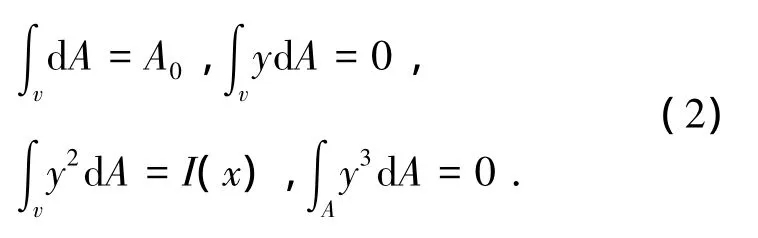
2 變截面梁單元位移插值函數
在有限元分析中,需要先確定位移模式,本文對位移增量場采用多項式插值,即:對軸向位移增量采用線性函數插值,對橫向位移增量采用三次函數插值,對轉角位移增量采用二次函數插值.如圖2所示,單元左右兩端橫向位移分別為yi、yj,相應的轉角位移記為 θi、θj,單元長度為 L.則單元位移可表示為
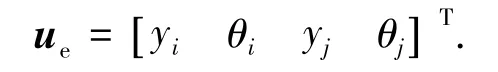
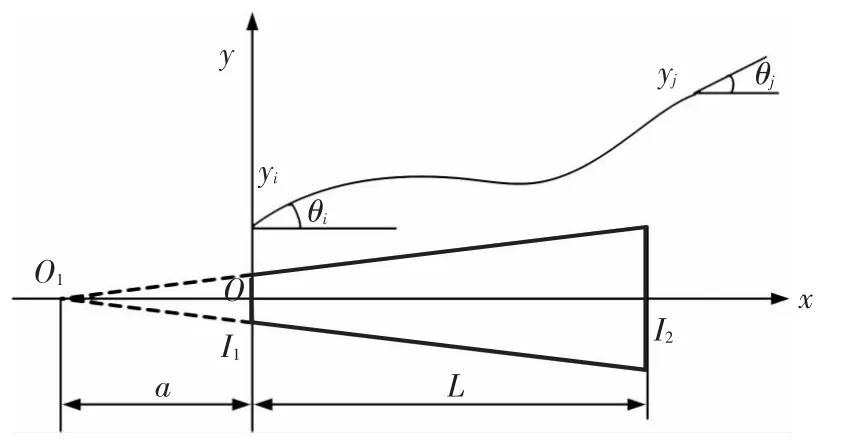
圖2 變截面梁單元的位移描述
根據勢能駐值原理,考慮剪切變形的單元總勢能為
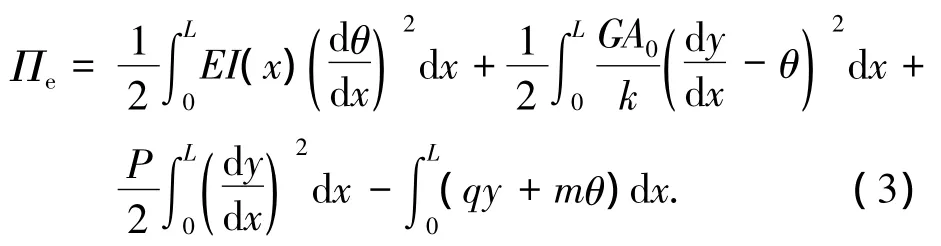
將式(3)列寫為矩陣形式有
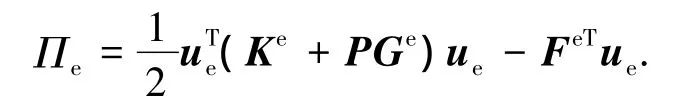
式中:Ke為單元線性剛度矩陣,Ge為單元幾何剛度矩陣,Fe為廣義載荷向量.
為了計入剪切變形影響,假設撓度函數ω(x)與轉角函數ψ(x)分別表示為
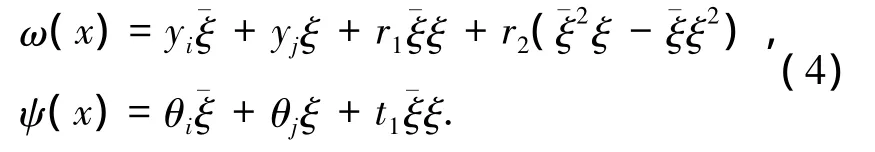
單元內部自由度r1、r2、t1的大小可由單元應變能確定,由式(3)可知,單元應變能表示為
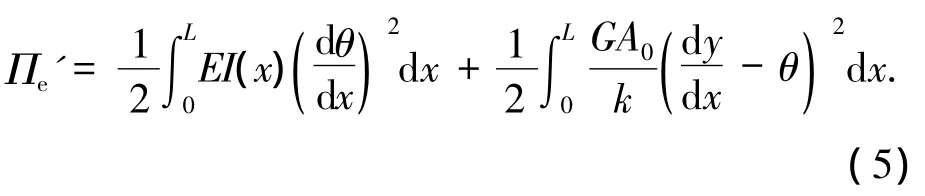
將式(4)代入式(5),積分后化為矩陣形式:
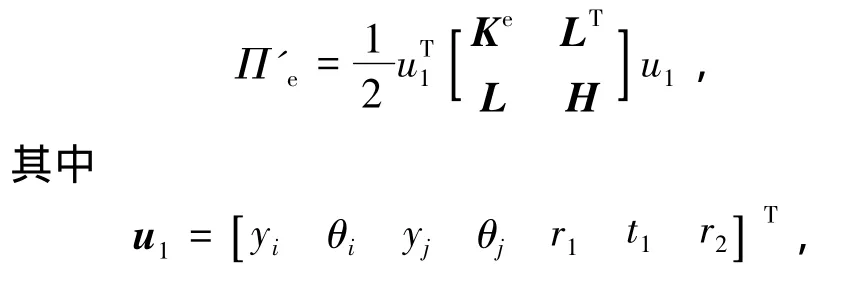
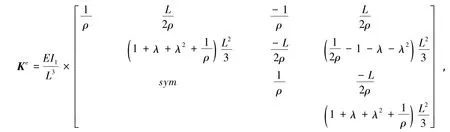
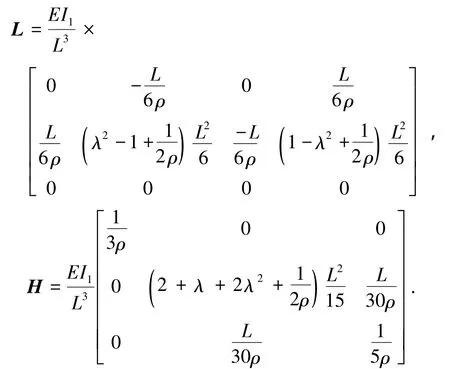
式中:ρ為量綱一的剪切系數,ρ=EI1k/(GAL2);λ為錐度系數L)/a;k為截面剪切校正因子.
系數 r1、r2、t1應使應變能 Πe'取最小值,故
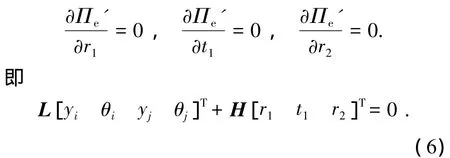
由式(6),利用靜力凝聚,將 r1、r2、t1用 yi、θi、yj、θj表示,得到已消除內部自由度的橫向位移與轉角

不難證明,當變截面錐度系數λ→1時,本文梁單元橫向位移與轉角表達式(7)、(8)將相應發生退化,退化后的表達式與文獻[9]中考慮剪切變形的等截面梁單元相同.
3 幾何非線性有限元增量平衡方程
采用U.L.列式法來建立梁柱單元的幾何非線性增量剛度方程.根據有限元理論,以t時刻位形為參考位形,建立梁單元U.L.格式下的虛功增量方程:
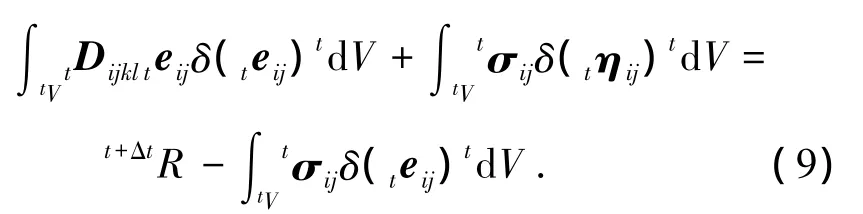
式中:Dijkl為單元本構關系矩陣;eij為格林應變張量線性項;ηij為格林應變張量非線性項;σij為單元柯西應力;t+ΔtR為t+Δt時刻外力所做的虛功.
本構關系矩陣為
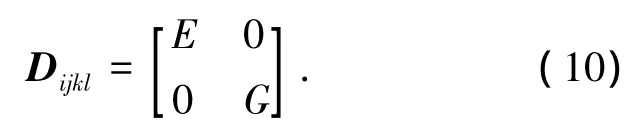
式中:E為彈性模量,G為剪切模量.
因為已知方程中所有的物理量都是以t時刻為基準來度量的,而t時刻為已知狀態,因此,在以下分析中省去左上角標及左下角標t.
將式(10)帶入式(9),并考慮應變分量與應變張量表達之間的關系,可得相應的虛功增量方程為
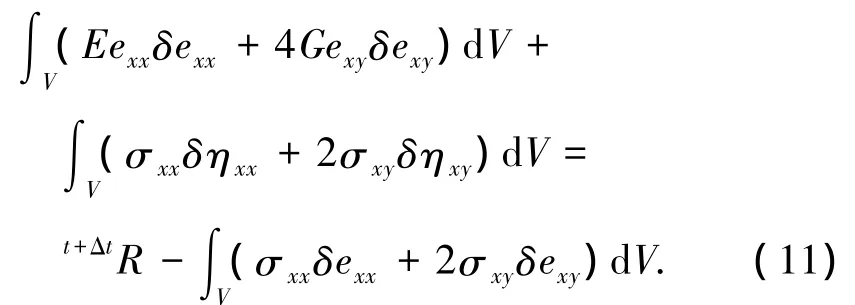
式中格林應變張量的線性項與非線性項表達如下:
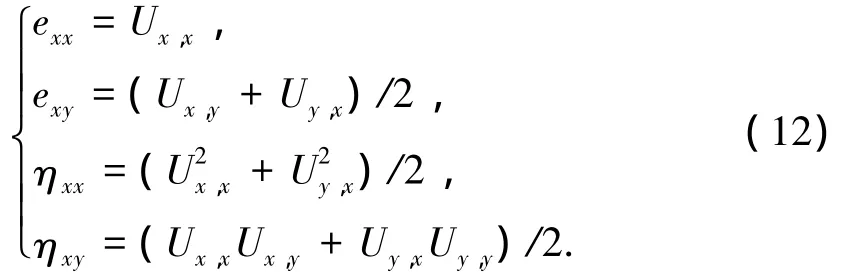
式中:“,”表示對后面坐標的導數,Ux0,Uy0為截面x形心處的位移增量,θ為截面x的轉動增量.
變截面梁單元任意截面x處的位移增量可表示為
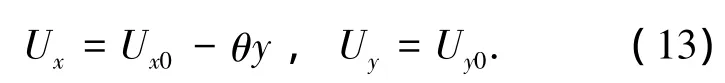
結合式(2)、(11)~(13)有如下關系式:
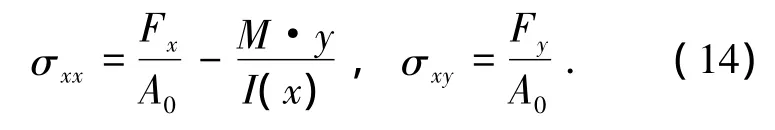
可得平面梁柱單元的虛功增量方程
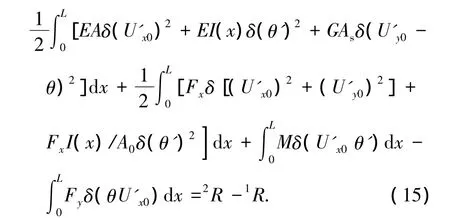
式中:As為單元抗剪切面積,As=A0/k;2R為t+Δt時刻外力所做虛功,即2R=t+ΔtR;1R為t時刻外力所做虛功,即
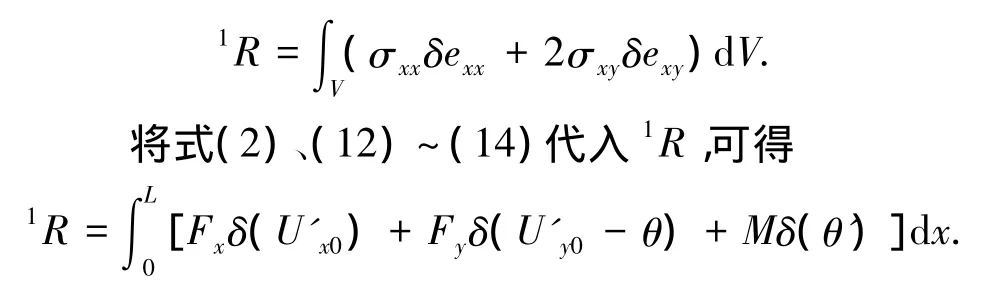
方程(15)即為平面梁柱單元的虛功增量方程,式中包括了軸向變形、剪切變形、彎曲變形以及它們之間的耦合項.
4 變截面梁單元之大位移剛度陣
平面變截面梁單元桿端力與桿端位移如圖3所示.
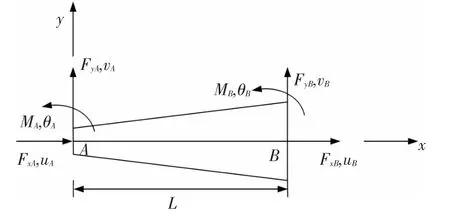
圖3 平面梁柱單元桿端力與桿端位移
單元節點位移向量
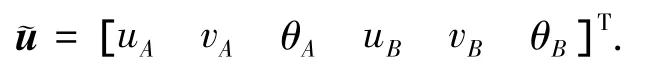
單元節點載荷向量
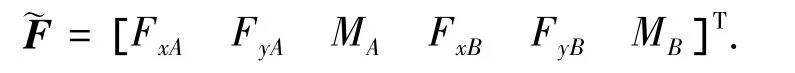
軸向位移選用線性函數插值,橫向位移與轉角采用式(7)、(8)考慮剪切變形的三次多項式插值.則單元任意截面質心處位移增量與桿端位移增量間的關系為

將單元截面內力用其桿端力表示為
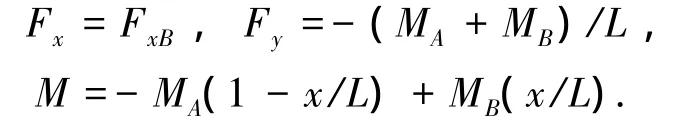
將式(1)、(16)、(17)代入單元虛功增量方程(15),可得三維梁柱單元的幾何非線性剛度方程
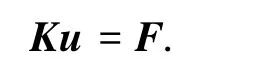
式中K即為慣性矩二次變化變截面梁柱單元的大位移切線剛度矩陣,其表達式為
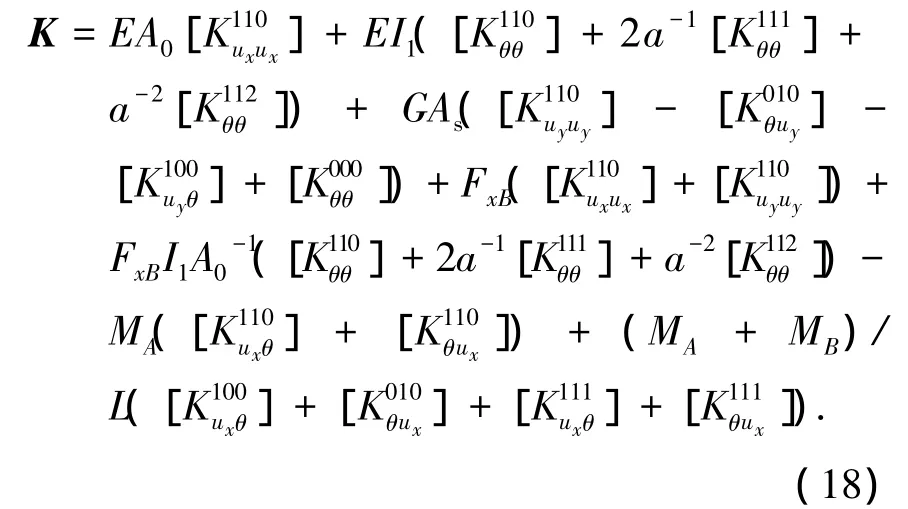
式中:
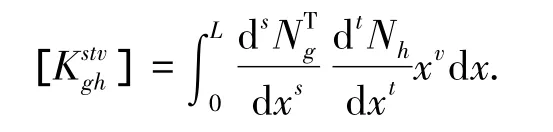
其中:下標g和h表示位移ux、uy或θ,上標s和t表示對位移插值函數N求導的階數,v則表示以x為底的冪函數的次數.
將式(17)帶入式(18),可得變截面梁單元大位移剛度矩陣
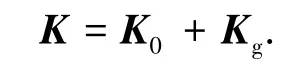
式中:K0為變截面梁單元之彈性剛度矩陣,Kg為變截面梁單元之幾何剛度矩陣.
線性剛度陣表達式為

幾何剛度陣表達式為

5 算例
算例1 如圖4所示典型的Williams曲肘,兩桿均為等截面直桿,兩端約束方式為固接,在曲肘頂點處施加豎向載荷 P.結構參數 L=657.5 mm,h=9.8 mm,a=19.126 mm,b=6.172 mm,彈性模量取E=71 GPa.計算在承受軸力P作用時頂點處的豎向位移δ,使用本文方法對該結構進行大位移非線性分析,每根桿件劃分為20個單元,計算所得結果與文獻[10]中Williams解析解進行比較,如圖5所示.
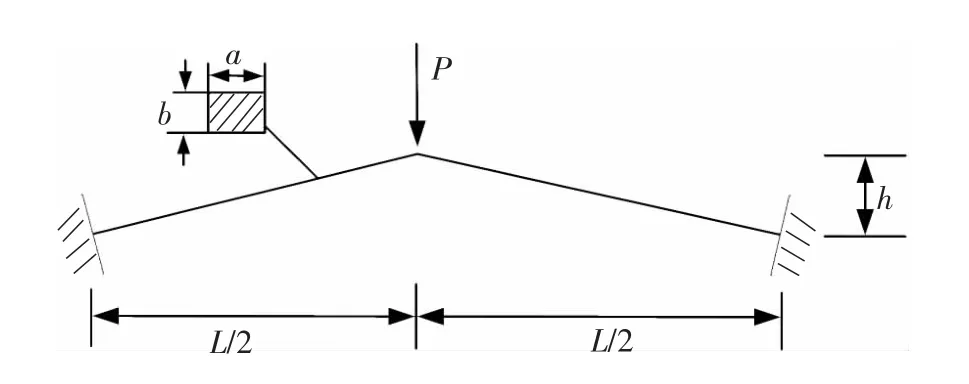
圖4 等截面Williams曲肘模型
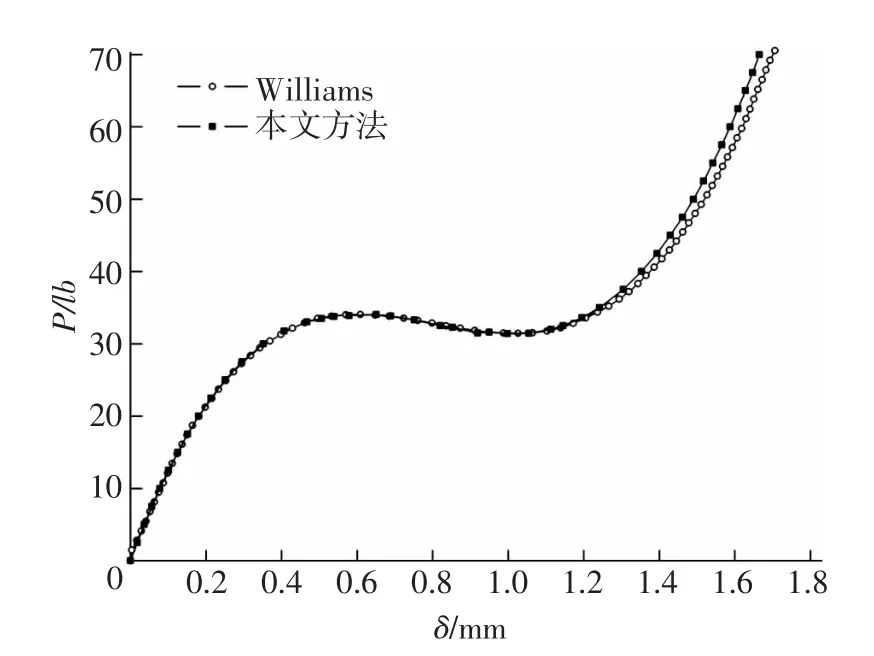
圖5 Willams曲肘軸向載荷位移曲線
由圖5可見,兩種方法所得結果吻合較好,證明了本文方法的有效性,本文推導的變截面梁單元退化得到的等截面梁單元在大位移非線性分析時,保持了較高的計算分析精度.
算例2 如圖6所示變截面懸臂梁,自由端承受橫向集中力Q作用.取構件小端截面面積A0=0.04 m2,小端截面慣性矩 I0=1.33×10-4m4,大端截面慣性矩為2I0,構件長度L=1.0 m,彈性模量E=200 GPa,剪切模量G=71 GPa,采用量綱一載荷κ=QL2/EI0,取截面剪切校正因子k=10/9,(x,y)表示梁桿軸線上任意點坐標值.本文將構件離散為20個單元進行計算,所得結果與ANSYS將構件劃分為20個單元的結果進行對比如表1所示.
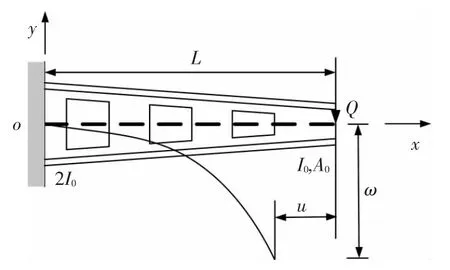
圖6 變截面懸臂梁模型
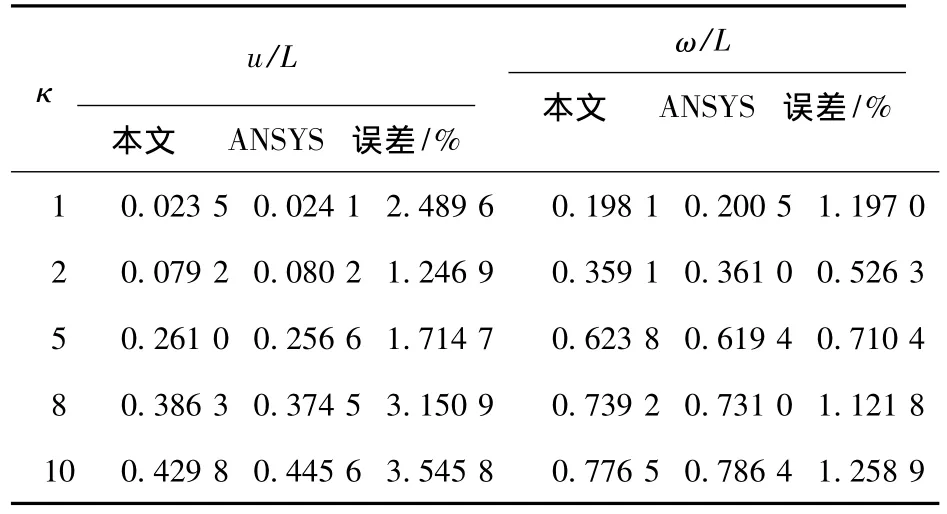
表1 本文方法與ANSYS大位移分析結果比較
圖7給出了κ=1、2、5、8、10時該懸臂梁大位移變形后的構型.圖中橫縱坐標分別為構件軸向坐標x、橫向坐標y與構件總長L的無量綱比值.
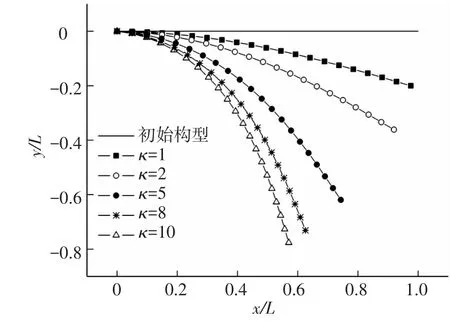
圖7 變截面懸臂梁大位移構型
在大位移情況下,構件自由端橫向位移隨剪切系數變化情況如圖8所示.可見,在相同載荷下,剪切剛度越弱,構件橫向位移越大,剪切剛度對慣性矩二次變化變截面構件幾何非線性影響較為顯著.
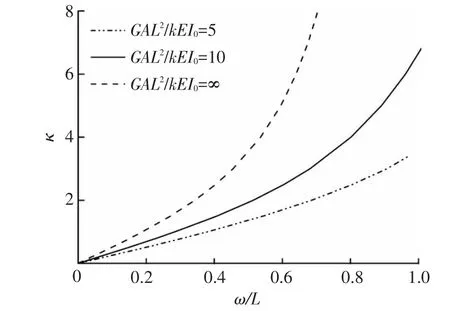
圖8 不同剪切系數下的橫向位移變化曲線
6 結論
1)利用多項式插值函數構造了計及剪切與變截面因素影響的位移場,采用U.L.列式法建立梁柱單元的幾何非線性虛功增量方程,得到同時考慮軸力、剪切、彎曲效應及其耦合項的慣性矩二次變化變截面梁單元大位移切線剛度陣.
2)本文方法嚴格計入了剪切變形與變截面因素的影響,具有較高的計算精度,適用于變截面梁、等截面梁以及組合式梁桿結構的大位移幾何非線性分析.
[1]BATHE K J.Finiteelementprocedures [M].Englewood Cliffs:Prentice Hall,1996:561-566.
[2]陳政清,增慶元,顏全勝.空間桿系結構大撓度問題內力分析的UL列式法[J].土木工程學報,1992,25(5):34-44.
[3]ARISTIZABAL-OCHOA J D.Large deflection and postbuckling behavior of Timoshenko beam-columns with semirigid connections including shear and axial effects[J].Journal of Engineering Structures,2007,29(6):991-1003.
[4]CHEN H H,LIN W Y,HSIAO K M.Co-rotational finite element formulation for thin-walled beams with generic open section [J].ComputerMethodsin Applied Mechanics and Engineering, 2006, 195(19):2334-2370.
[5]張宏生.桿系結構幾何非線性動靜態分析方法及其在塔機中的應用[D].哈爾濱:哈爾濱工業大學,2009.
[6]郭彥林,王文明,石永久.變截面門式剛架結構的非線性性能[J].工程力學,2000,17(4):29-36.
[7]LIEW J Y R,CHEN H,SHANMUGAM N E,et al.Improved nonlinear plastic hinge analysis of space frame structures[J].Engineering Structures,2000,22(10):1324-1338.
[8]REMKE J,ROTHERT H.Eine geometrisch nichtlineare finite-element berechnung raumlicherstabtragwerke mittels einer Abspaltung von starrkorperbewegungen[J].Bauingenieur,1999,74:139-147.
[9]王勖成.有限單元法[M].北京:清華大學出版社,1997:278-292.
[10]WILLAMS F W.An approach to the non-linear behavior of the members of a rigid jointed plane framework with finite deflections[J].Quarterly Journal of Mechanics and Applied Mathematics,1964,17(4):451-469.
Geometric nonlinear analysis of tapered beam with inertia moment vary quadratic
MENG Lixia,LU Nianli,LIU Shiming
(School of Mechatronics Engineering,Harbin Institute of Technology,150001 Harbin,China)
To research the geometric nonlinear problem of tapered beam with shear deformation,based on Timoshenko theory,the displacement and rotation independent interpolation method was adopted to obtain the shape functions of tapered beam considering shear deformation,whose inertia moment varied quadratic.Then,started from the virtual work increment equation,the geometric nonlinear incremental equilibrium equation of the plane tapered beam element was established,including axial force,shear effect,bending effect and its coupling term,and the large displacement tangential stiffness matrix of the tapered beam was obtained.Finally,the classical examples are calculated,and the results show that the proposed method is accurate and effective.
finite element method;tapered beam;virtual work increment equation;large displacement;geometric nonlinear
TU311.2
A
0367-6234(2014)03-0020-06
2013-03-29
國家科技支撐計劃資助項目(2011BAJ02B01-02).
孟麗霞(1983—),女,博士研究生;
陸念力(1955—),男,教授,博士生導師.
孟麗霞,Menglixia1983@163.com.
(編輯 楊 波)

