自抗擾技術在四旋翼飛行姿態控制中的應用

李 毅，陳增強，劉忠信

(1.南開大學天津市智能機器人技術重點實驗室，300071 天津;2.南開大學計算機與控制工程學院自動化系，300071 天津)

自抗擾技術在四旋翼飛行姿態控制中的應用

李 毅1，2，陳增強1，2，劉忠信1，2

(1.南開大學天津市智能機器人技術重點實驗室，300071 天津;2.南開大學計算機與控制工程學院自動化系，300071 天津)

介紹了自抗擾控制器的結構組成，包括跟蹤微分器、擴張狀態觀測器以及非線性狀態誤差反饋律，并給出了各部分的典型算法.針對四旋翼盤旋系統的姿態控制問題，設計了連續型和離散型兩種自抗擾控制器，在Simulink下搭建了仿真結構圖，并進行了參數整定.仿真結果表明，文中所設計的自抗擾控制器可以滿足控制精度及快速性的要求，并且具有強魯棒性、抗干擾性能以及對非線性強耦合系統的解耦能力.

自抗擾控制技術;跟蹤微分器;擴張狀態觀測器;四旋翼系統

PID控制器是不依賴于被控對象的精確數學模型，只用控制目標與對象實際輸出之間的誤差來產生消除此誤差的控制策略，所以，其在控制工程實踐中得到了廣泛的應用.然而，隨著科學技術的發展對控制精度、控制速度以及對環境變化的適應能力的要求越來越高，經典PID的缺點逐漸顯露出來.

自20 世紀 80 年代開始，韓京清［1－2］在面對帶有更多內部和外部不確定因素的控制對象時，PID控制器無能為力的情況下，研究出了“自抗擾控制技術”(Active Disturbance Rejection Control Technique，ADRC).自抗擾控制技術［3］一經誕生，就成為研究非線性系統的有效工具，并在許多理論研究、試驗和工程實際中得到了迅速的推廣應用.

自抗擾控制技術是一種不依賴于系統模型的新型控制技術，它能夠實時估計并補償系統在工作時受到的各種外擾以及系統自身機理決定的內擾的總和擾動作用，結合特殊的非線性狀態誤差反饋機制，就可以得到優良的控制品質.自抗擾控制技術具有超調小、響應速度快、控制精度高、抗干擾能力強及算法簡單的特點.并且，該技術特別適合于數字化實現，完全順應了數字化發展的趨勢.

四旋翼飛行器是一個具有六自由度(位置和姿態)和4個控制輸入的欠驅動系統，其具有多變量、非線性、強耦合和對擾動敏感的特性，這使得飛行控制系統的設計變得十分困難，而整個飛行控制的關鍵就是姿態控制.目前相關的控制方法 包 括 四 元 反 饋 控 制［4－5］、Backstepping［6］、LQ［7］等.

1 自抗擾控制器的基本原理

自抗擾控制器由跟蹤微分器(Tracking Differentiator，TD)、擴張狀態觀測器(Extended State Observer，ESO)和非線性狀態誤差反饋律(Nonlinear State Error Feedback，NLSEF)3部分組成.如圖1所示，虛線框中的部分即為自抗擾控制器.

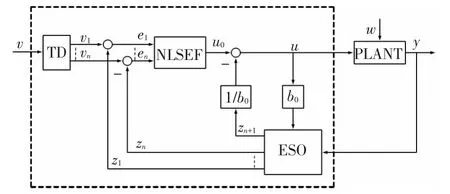
圖1 自抗擾控制器組成

1.1 跟蹤微分器(TD)

跟蹤微分器是為系統輸入安排過渡過程，得到光滑的輸入信號以及輸入信號的微分信號.以二階系統為例，一種離散形式的非線性跟蹤微分器算法如下:

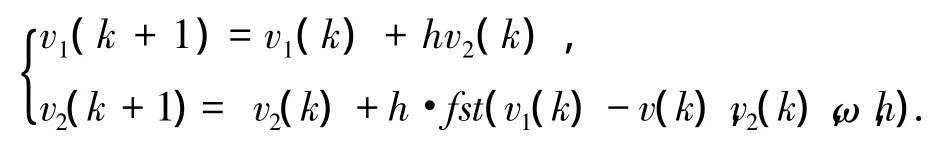
式中:h為采樣周期，v(k)為第k時刻的輸入信號，ω為決定跟蹤快慢的參數，fst()函數為最速控制綜合函數，描述如下:

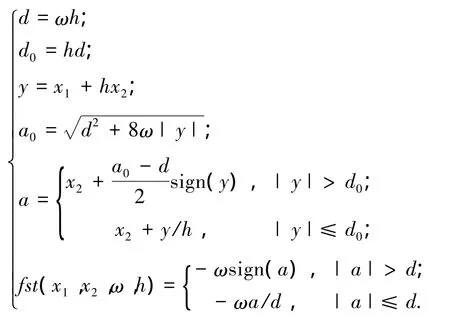
采用上述微分器，則可實現 v1(k)→v(k)，v2(k)→˙v(k).并且，如果v(k)是帶有噪聲的信號，微分器可同時實現濾波.

1.2 擴張狀態觀測器(ESO)

擴張狀態觀測器可以估計出系統的狀態和總擾動.其中，總擾動是指系統自身模型的不確定性(內擾)和系統的外部擾動(外擾)的綜合作用.將ESO估計出來的總擾動量補償到控制器中去，就可以使原來的非線性系統轉變為線性的積分器串聯型控制系統.上述動態估計補償總和擾動的技術，就是自抗擾控制技術的最核心技術.

一種連續形式的ESO算法如下:

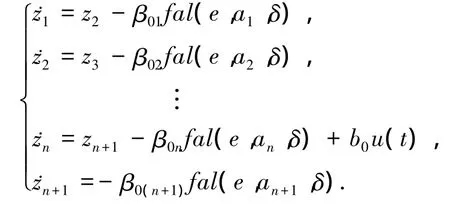
一種離散形式的ESO算法如下:

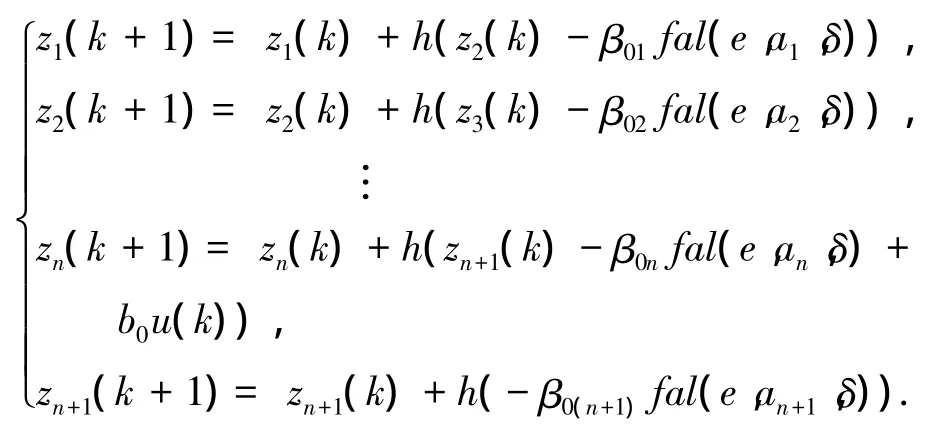
式中:h為采樣周期，β01～ β0(n+1)，a1～ an+1均為可調參數，δ為線性段的區間長度，fal()函數為

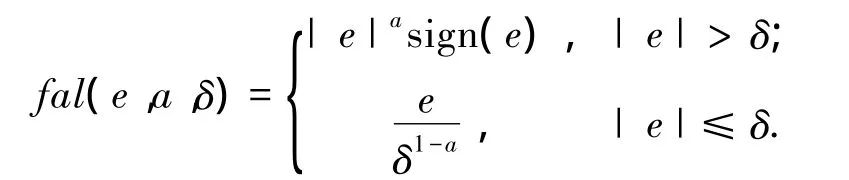
1.3 非線性狀態誤差反饋律(NLSEF)

非線性狀態誤差反饋律是通過非線性函數，將TD產生的跟蹤信號及其微分信號與ESO估計出的系統的狀態進行適當的組合，最終作為系統的控制量.

以二階系統為例，一種采用fal()函數組合的NLSEF算法為

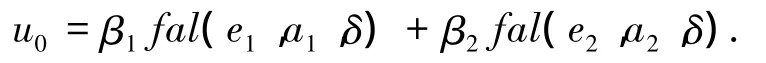
式中:β1、β2為可調參數.系統的狀態誤差是指e1=v1-z1，e2=v2-z2.對誤差反饋控制量u0，用總擾動估計值z3的補償來決定最終控制量:

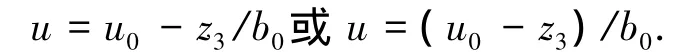
式中可調參數b0是決定補償強弱的“補償因子”.

2 四旋翼飛行姿態控制仿真

采用由加拿大Quanser公司生產的四旋翼盤旋實驗裝置，來研究姿態的控制問題.在Matlab的Simulink下，將使用連續和離散兩種自抗擾控制技術進行仿真.

2.1 四旋翼盤旋系統的模型

三自由度(姿態)四旋翼盤旋系統的狀態空間方程［8－9］為

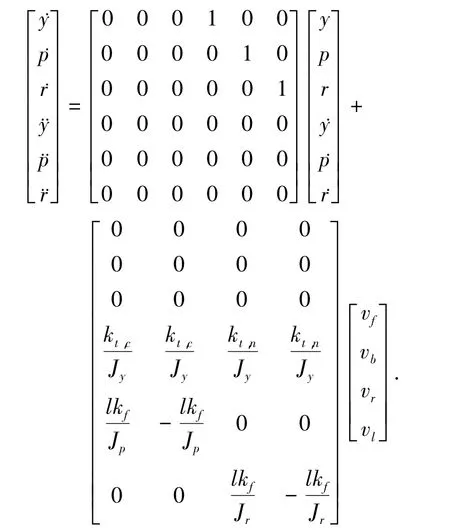
式中:y為偏航角;p為俯仰角;r為滾轉角;vf、vb、vr、vl分別為控制前、后、右、左4個旋翼轉速的電壓.Kt，n為順時針螺旋槳推力矩系數，其值為 0.003 6 N·m/V;Kt，c為逆時針螺旋槳推力矩系數，其值為 -0.003 6 N·m/V;Kf為螺旋槳推力系數，其值為0.118 8 N/V;Jy為偏航軸轉動慣量，其值為0.110 4 kg·m2;Jp、Jr分別為俯仰軸、滾轉軸轉動慣量，其值均為0.055 2 kg·m2;l為旋轉中心到螺旋槳中心的距離，其值為0.197 m.

2.2 基于Simulink仿真

將三自由度四旋翼盤旋系統分為偏航、俯仰和滾轉3個通道，則姿態控制［10－11］框圖如圖2所示.依照圖2，在Simulink下搭建模塊，如圖3所示.圖3中，由上至下，3部分分別為偏航通道、俯仰通道和滾轉通道;由左至右，標識圈內分別為設定值、跟蹤微分器、非線性狀態誤差反饋律、擴張狀態觀測器、控制量轉換、四旋翼系統和示波器.

系統初始值為 x0=［－3°，－3°，－3°，0，0，0］，仿真時間為20 s.每個通道的設定值均為:幅值為3°，頻率為0.1 Hz的方波信號.

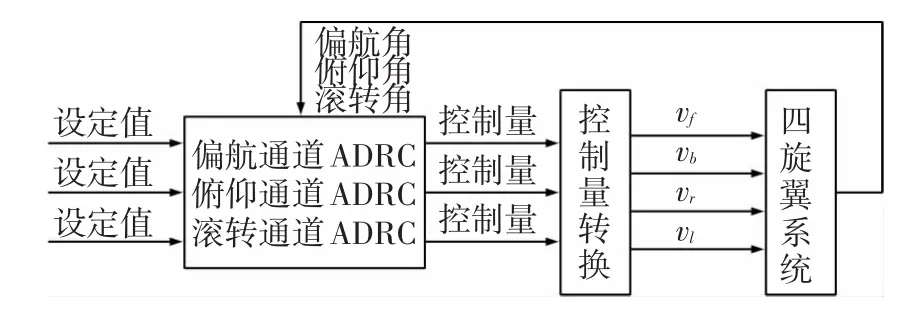
圖2 姿態控制框圖

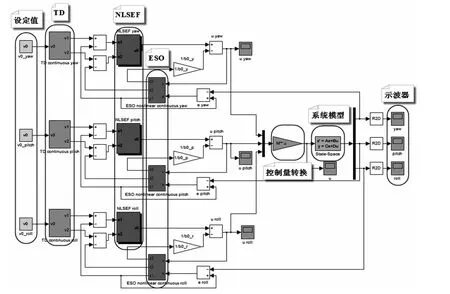
圖3 Simulink仿真結構

連續型ADRC的主要參數為

連續型ADRC姿態控制仿真結果如圖4所示.

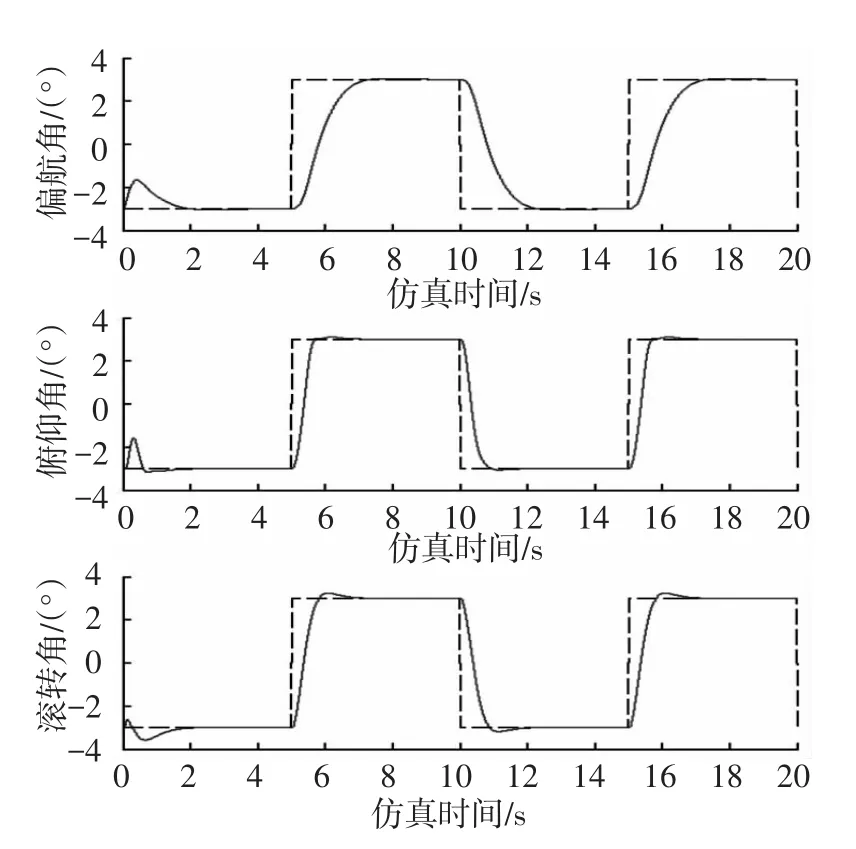
圖4 連續型ADRC姿態控制仿真

離散型ADRC的主要參數為

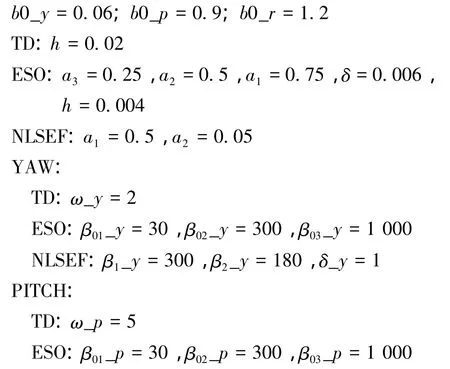
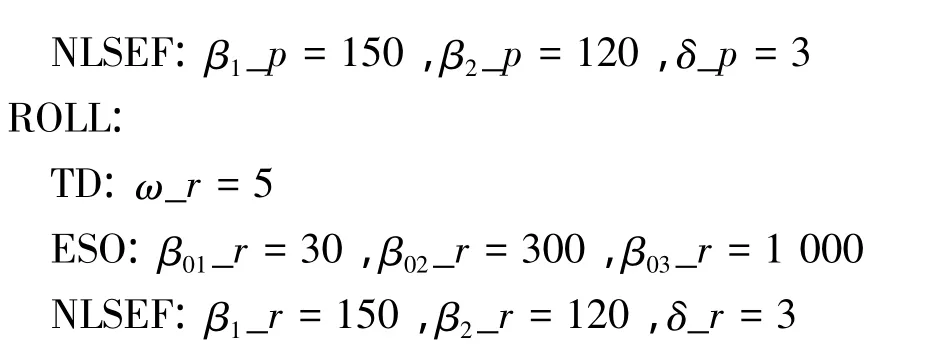
離散型ADRC姿態控制仿真結果如圖5所示.

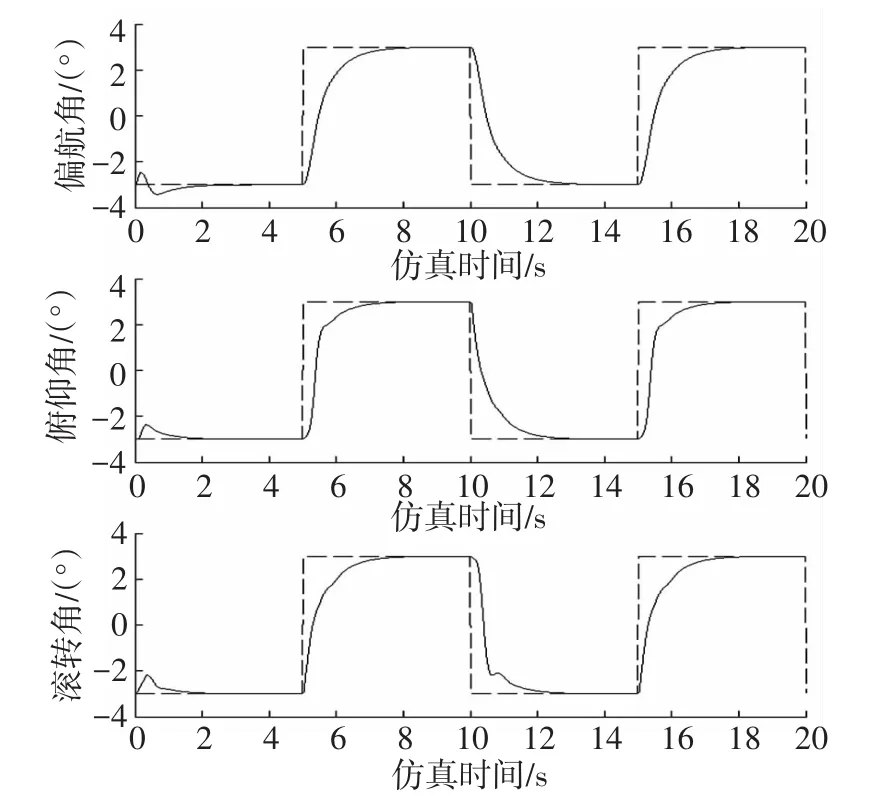
圖5 離散型ADRC姿態控制仿真

由圖4、5可以看出，文中所設計的ADRC控制器無論是連續型還是離散型，經過簡易的參數的整定，都可以使偏航角、俯仰角和滾轉角在比較惡劣的初始條件下，以很短的時間達到設定值，體現了控制器的快速性和穩定控制能力.同時，在設定值具有較大突變的情況下，ADRC控制器也能取得良好的控制效果，這體現了控制器是具有一定魯棒性的.對比連續型和離散型ADRC:在精度要求上，離散型ADRC要好一些，無超調，無振蕩.而從快速性以及調節參數的難易程度來說，連續型ADRC更勝一籌.總體來說，兩個仿真效果令人滿意.

3 結語

針對具有獨特機械結構的四旋翼欠驅動系統，設計了連續型和離散型兩種自抗擾控制器，并在Simulink環境下搭建了姿態控制仿真圖.通過參數整定，得到了優良的仿真結果.這表明，文中所設計的自抗擾控制器具有強魯棒性、抗干擾性能以及對非線性強耦合系統的解耦能力.

［1］韓京清.自抗擾控制器及其應用［J］.控制與決策，1998，13(1):19－23.

［2］韓京清.從PID技術到“自抗擾控制”技術［J］.控制工程，2002，9(3):13－18.

［3］姜萍，郝靖宇，宗曉萍，等.自抗擾控制器的simulink建模與仿真［J］.自動化技術與應用，2010，29(2):1－4.

［4］TAYEBI A，MCGILVRAY S.Attitude stabilization of a four-rotor aerial robot［C］//Proceedings of the 43rdIEEE International Conference on Decision and Control.Paradise Island:IEEE，2004，2:1216－1221.

［5］JOSHI S M，KELKAR A G，WEN J T Y.Robust attitude stabilization ofspacecraftusing nonlinear quaternion feedback［C］//IEEE Transactions on Automatic Control，［s.l.］:［s.n.］，1995，40(10):1800－1803.

［6］BOUABDALLAH S，SIEGWART R.Backstepping and sliding-mode techniques applied to an indoor micro quadrotor［C］//Proceedings of the 2005 IEEE International Conference on Robotics and Automation.Barcelona:IEEE，2005，2247－2252.

［7］BOUABDALLAH S，NOTH A，SIEGWART R.PID vs LQ control techniques applied to an indoor micro quadrotor［C］//Proceedings of the 2004 IEEE/RSJ InternationalConference on IntelligentRobotsand Systems.Sendal:IEEE，2004，3:2451－2456.

［8］劉志軍，呂強，王東來.小型四旋翼直升機的建模與仿真控制［J］.計算機仿真，2010，27(7):18－20.

［9］于衛衛.三自由度四旋翼盤旋系統控制問題研究［D］.沈陽:東北大學，2007.

［10］王俊生，馬宏緒，蔡文瀾，等.基于ADRC的小型四旋翼無人直升機控制方法研究［J］.彈箭與制導學報，2008，28(3):31－34.

［11］李杰，齊曉慧，韓帥濤.基于自抗擾技術的四旋翼姿態解耦控制方法［J］.電光與控制，2013，20(3):44－48.

Attitude control of a quad-rotor robot based on ADRC

LI Yi1，2，CHEN Zengqiang1，2，LIU Zhongxin1，2

(1.Tianjin Key Laboratory of Intelligent Robotics，Nankai University，300071 Tianjin，China;2.Dept.of Automation，College of Computer and Control Engineering，Nankai University，300071 Tianjin，China)

In this paper，the structure of the active disturbance rejection control technique is described in detail，including the tracking differentiator，extended state observer and nonlinear state error feedback.Typical algorithms of each part are given as well.In order to control the attitude of the quad-rotor robot as we desired，we design two kinds of ADRC，including the continuous ADRC and the discrete ADRC.Simulations were carried out based on Simulink.After parameter adjustment，the simulation results show that the ADRC can meet the need of control accuracy and swiftness of response.It also indicates that the controller has strong robustness and anti-disturbance performance，which can control the nonlinear coupling systems effectively.

ADRC;tracking differentiator;extended state observer;quad-rotor robot

V278

A

0367－6234(2014)03－0115－04

2013－10－23.

國家自然科學基金資助項目(61174094，61273138);

天津市自然科學基金資助項目(13JCYBJC17400);

教育部優秀新世紀人才支持計劃(NCET-10-0506).

李 毅(1987—)，男，博士研究生;

陳增強(1964—)，男，教授，博士生導師;

劉忠信(1975—)，男，教授，博士生導師.

李 毅，aiai102410@163.com.

(編輯 苗秀芝)