含摩擦的雙電機伺服系統快速終端滑模控制

趙 威，任雪梅

(北京理工大學自動化學院，100081 北京)

含摩擦的雙電機伺服系統快速終端滑模控制

趙 威，任雪梅

(北京理工大學自動化學院，100081 北京)

針對含LuGre穩態摩擦力的雙電機伺服系統，通過引入含速度項的指數函數，提出一種連續可微的LuGre穩態摩擦模型，解決了原有模型不可微的缺點，該模型能夠有效刻畫Stribeck現象、庫倫摩擦、粘滯摩擦等多種摩擦特征;為了進一步解決系統的同步和跟蹤問題，基于該連續可微摩擦模型，引入表征同步率的可變系數設計了可變系數的快速終端滑模控制器，并運用Lyapunov方法證明了在給定控制律下，系統能夠實現先同步控制后跟蹤控制.仿真結果表明提出的控制方法具有快速收斂速度和高跟蹤精度.

雙電機伺服系統;快速終端滑模;連續LuGre摩擦模型;跟蹤控制;同步控制

隨著控制精度要求以及控制過程復雜性的提高，多電機系統控制算法的設計日益復雜.由于存在摩擦等非線性因素的影響，如何設計控制器保證電機的高精度跟蹤和同步控制已經成為一個熱點問題.

摩擦是伺服系統中普遍存在的一種非線性現象，它對系統產生許多負面影響，影響了閉環系統的性能，尤其在低速運行時更明顯.由于LuGre模型能夠很好地描述復雜摩擦現象，許多學者致力于LuGre摩擦的建模和補償控制研究.Muvengei等［1］和Wang等［2］分別研究LuGre摩擦模型的建模以及參數識別方法.在摩擦補償方面，文獻［3－4］提出了基于觀測器的摩擦補償算法，并證實了觀測器可以消除摩擦的影響并能有效改善控制精度.向紅標等［5］采用基于LuGre模型的 Backstepping方法設計自適應摩擦補償控制器.本文在此基礎上，提出一種連續可微的摩擦模型代替LuGre穩態摩擦，來解決原模型不可微的缺點.

此外，由于控制精度要求的不斷提高，電機的快速高精度控制也成為許多學者關注的熱點.Wang等［6］設計了基于零相位誤差跟蹤控制器，提高電機系統的魯棒性能以及頻率響應性能.Liu等［7］基于誤差反向傳播神經網絡提出主動擾動抑制控制算法，提高了系統性能.Zhang等［8］提出一種方法實現多個電機速度同步并保證電機同步速度在一個可控的范圍.文獻［9－10］分別將H∞理論以及BP神經網絡與滑模控制方法結合設計控制器，從而保證快速跟蹤性.以上文獻只單獨考慮跟蹤或同步問題，而這兩個問題同等重要.因此，本文設計可變系數的快速終端滑模控制器，來達到先同步后跟蹤的控制目的.

考慮含有LuGre穩態摩擦的雙電機伺服系統，提出連續可微LuGre穩態摩擦模型，并考慮滑模控制高精度和魯棒性的特點，在原有滑模控制基礎上引入表征同步率的可變系數，提出了一種基于可變系數的快速終端滑模控制策略，從而達到快速同步和高精確跟蹤的控制目的.

1 模型構建

考慮雙電機伺服系統模型如下:

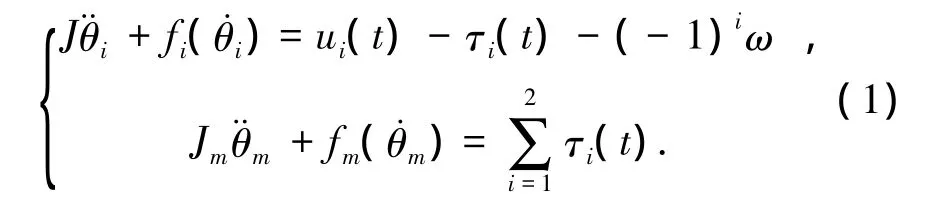
式中:θi(i=1，2)和θm分別表示電機和負載的轉角(i=1，2)和分別表示電機和負載的轉速;J表示電機的轉動慣量;Jm表示負載的轉動慣量;ui是系統輸入轉矩;ω是偏置力矩;τi代表電機和負載之間傳輸力矩;fi和fm分別表示與電機轉速和負載轉速有關的LuGre穩態摩擦力矩.

為了解決原有LuGre穩態摩擦模型不連續且不可微缺點對控制器設計造成的不便，用連續可微函數式(2)代替原有摩擦項:

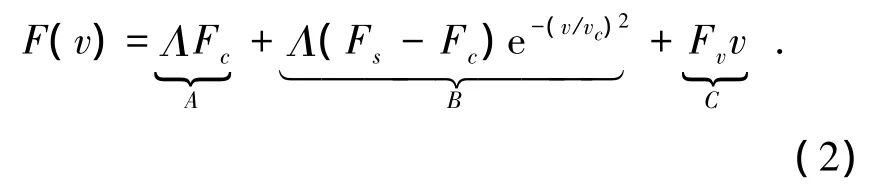
式中:v代表轉速，Λ =2/(1+e-γv)-1，γ ＞ 0，且γ的大小影響到F(v)與LuGre穩態摩擦模型間的擬合誤差，γ的取值越大，擬合精度就越高，如圖1所示，該連續可微模型能夠有效刻畫庫倫摩擦(A項)、Stribeck現象(B項)以及粘滯摩擦(C項)的摩擦特征.

將所提出的連續可微函數式(2)代入伺服系統模型(1)中可得新的系統模型為

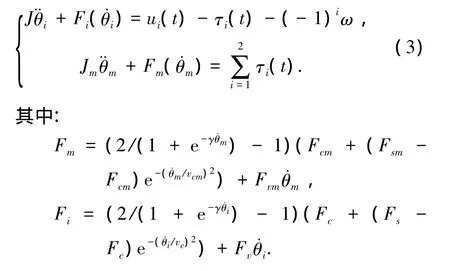
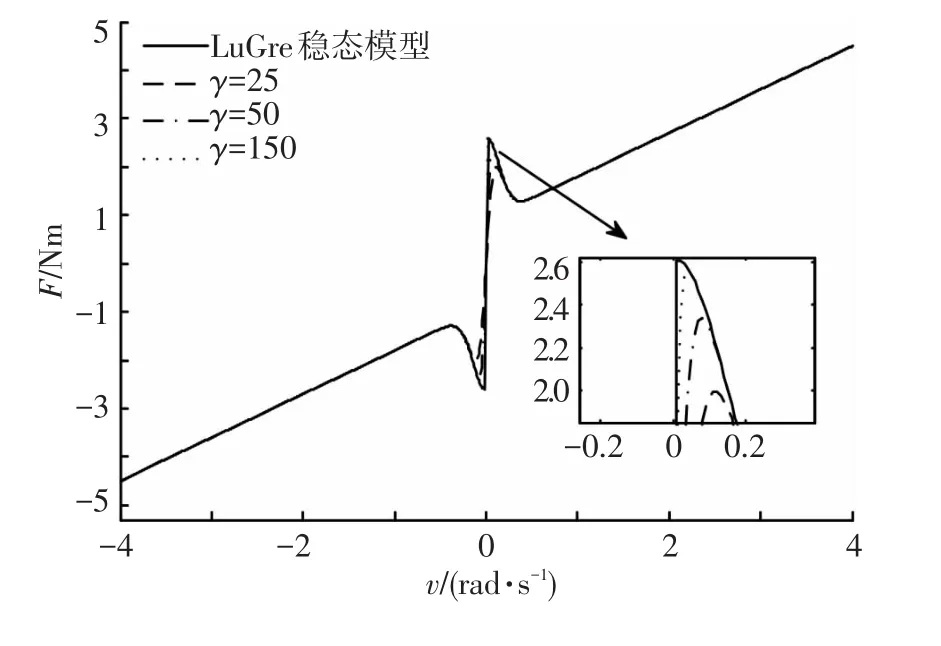
圖1 連續LuGre穩態模型

基于系統模型(3)，假設系統傳動比是1，且齒隙為2α.因為齒隙具有非線性特性，所以傳輸力矩τi(t)可表示為

式中k和c分別表示扭矩系數和阻尼系數，并且死區函數f(zi(t))定義為

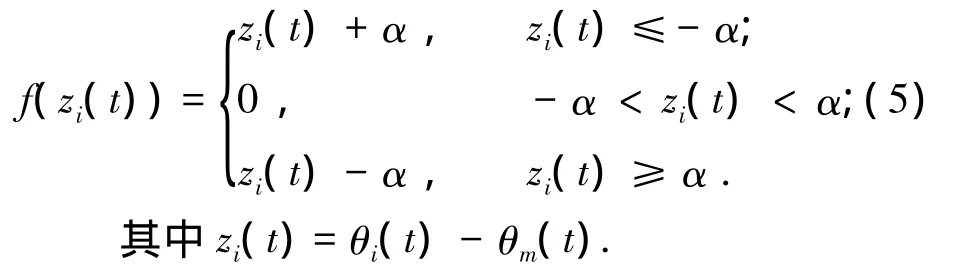
由于死區的非線性不利于設計控制器，因此我們運用如下的光滑、連續、可微的函數來代替死區函數

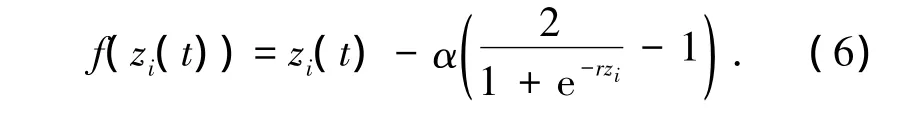
那么，傳輸力矩τi(t)可改寫為

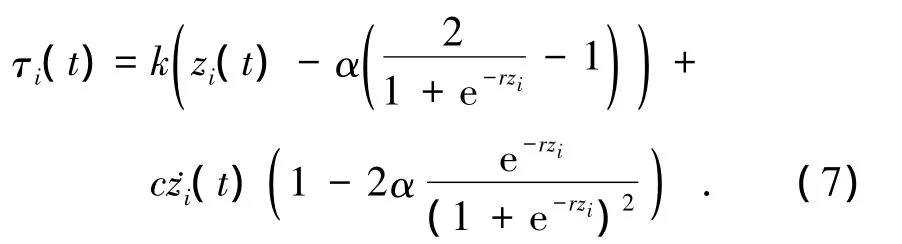
其中r＞0.

為了便于設計控制器，選擇 x1，x2，x3i，x4i為狀態變量

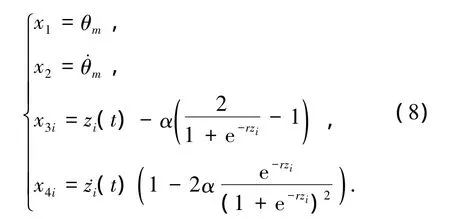
并且 τi(t)=kx3i+cx4i.

于是，狀態方程可表示為

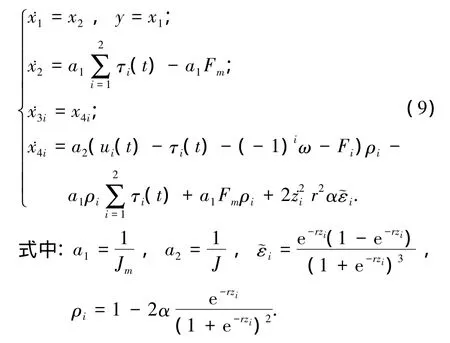
本文主要目的是設計相應的快速終端滑模控制器，使系統輸出精確跟蹤參考信號并完成2電機之間的同步控制.下面，我們對這個方面進行詳細介紹.

2 控制器設計

為了確保系統輸出能夠精確跟蹤參考信號，研究跟蹤誤差e(t)=y(t)-yd(t)的穩態性能.通過簡單的推導，可得下列等式

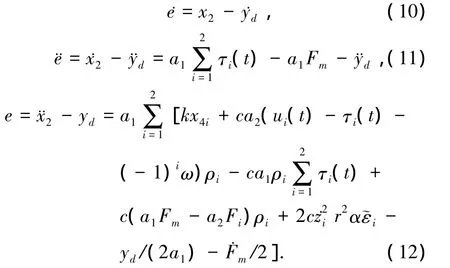
定義快速終端滑模為

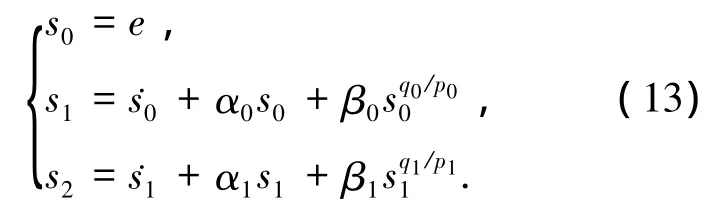
式中:pi＞ qi是正奇數，而 αi＞ 0，βi＞ 0.

為了能夠達到跟蹤與同步控制的目的，本文引入一個表征同步程度的可變系數，將原有滑模控制分為兩部分，即保證速度同步部分usi和不能速度保證同步部分uti.

基于連續LuGre穩態摩擦模型，控制量ui可表示為

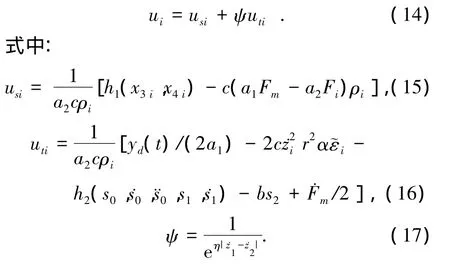
這里，b＞0，并且η是一個足夠大的正常數，而 h1(x3i，x4i)為系統的狀態反饋項，h1(x3i，x4i)=為滑模項，且

可變系數ψ反映兩電機轉速的同步程度，當兩電機轉速差較大時，ψ變小，保證速度同步部分的控制量usi起主要作用，兩電機逐漸達到同步狀態;當轉速差較小時，ψ趨近于1，控制量變為原有的滑模跟蹤控制，從而完成跟蹤目的，因此選擇合理的η，能夠保證系統達到先同步后跟蹤的目的.

以下，將對整個系統的穩定性進行分析.

定理1 考慮狀態方程(9)，控制率由式(14)～(17)給出，那么兩電機的轉速將會達到同步，并且跟蹤誤差e一致收斂.

證明 通過兩個步驟對整體的穩定性進行證明，即兩電機同步穩定性和輸出跟蹤穩定性.

首先，選擇以下Lyapunov函數證明兩電機同步穩定性，

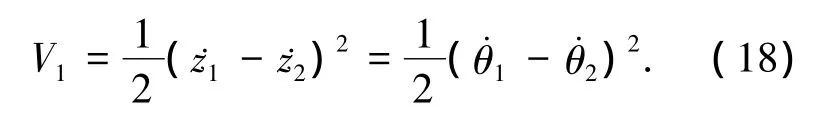
對式(18)進行求導，并將式(3)代入可得

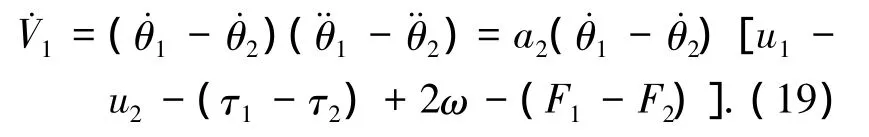
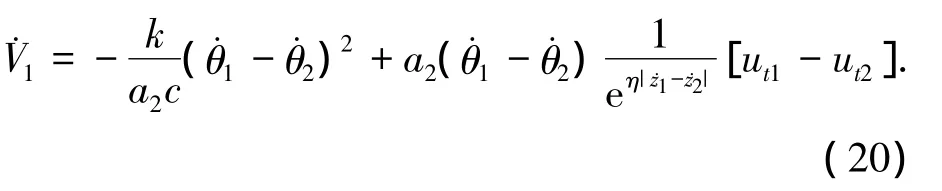
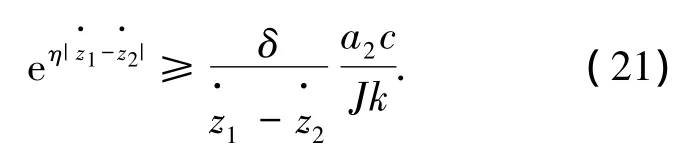
其中δ=ut1-ut2.

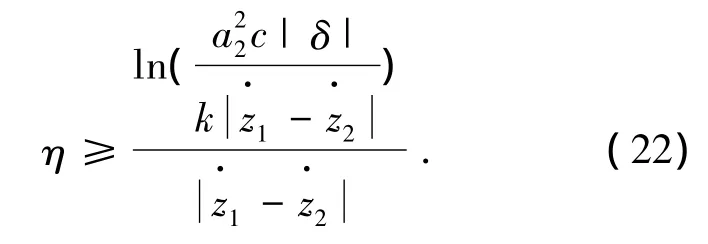
由于式(22)右端函數是有界函數，這里假設該函數上界為σ，那么當且僅當η≥σ時電機能夠達到同步.

下面選取另一個Lyapunov函數證明跟蹤誤差的穩定性.

對式(23)求導并將控制量代入得

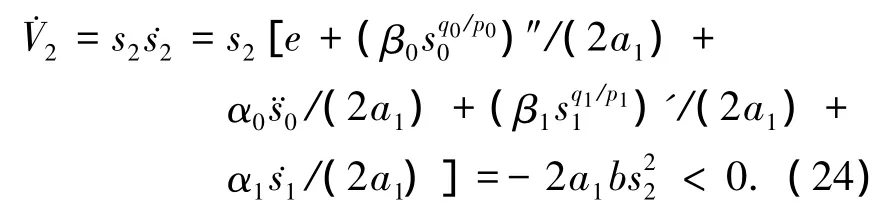
由上述推導可得，在控制率ui的作用下，系統能夠達到同步，并且跟蹤誤差e一致收斂.

3 仿真研究

為了驗證文中方法的有效性，將對系統的位置跟蹤和速度同步進行仿真研究.仿真以雙電機伺服系統為研究對象，其系統參數如表1所示.

表1 雙電機伺服系統參數

仿真中，選取yd=2sin(2/5πt)為跟蹤信號，應用式(14)～(17)所給出的控制率對系統進行控制.設計參數選擇如下:α0=46，α1=56，β0=10，β1=65，p0=11，q0=9，p1=9，q1=7，r=8.005，b=350，其中可變系數ψ的參數選擇為η=300.

位置跟蹤和速度同步仿真結果如圖2～5所示.

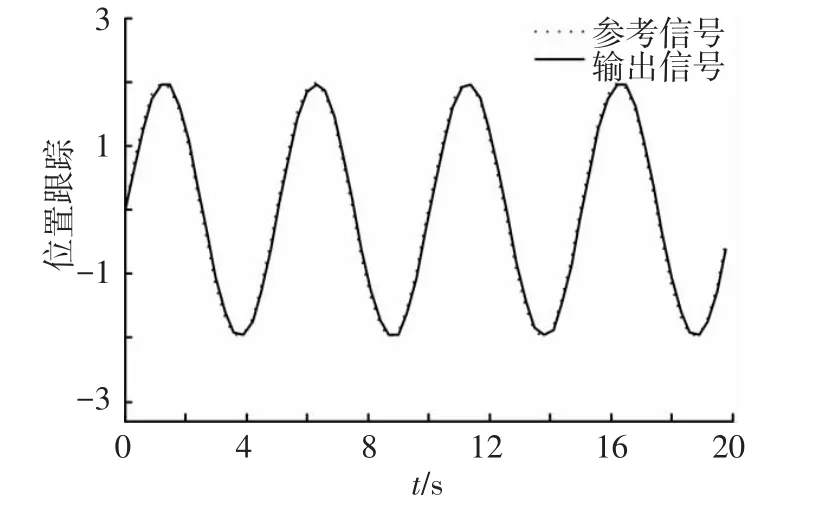
圖2 位置跟蹤結果

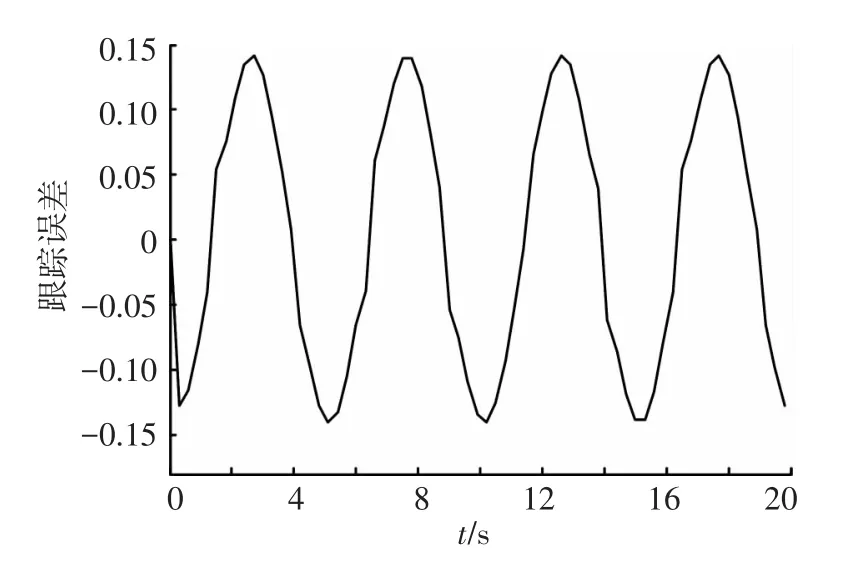
圖3 位置跟蹤誤差

圖 2、3為跟蹤控制的結果，圖 4、5給出了同步控制的結果.從仿真結果可以看出，文中提出的方法具有很好的控制性能，即具有較快的收斂速度和較小的誤差，該方法既能保證兩電機快速達到同步，又能保證輸出高精度跟蹤參考信號.

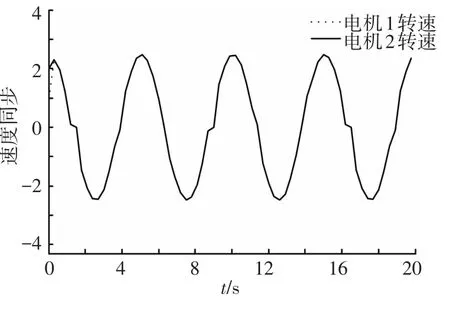
圖4 兩電機速度同步結果

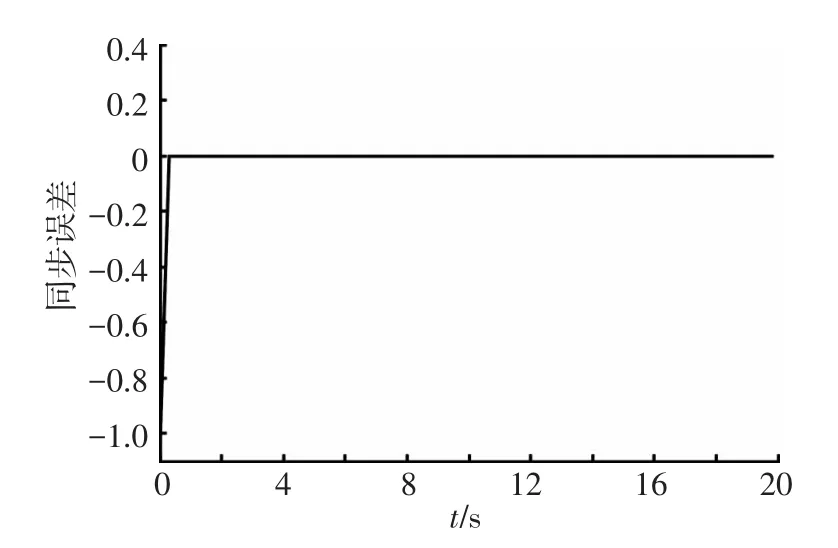
圖5 兩電機速度同步誤差

4 結語

本文考慮了含LuGre穩態摩擦項的雙電機伺服系統同步和跟蹤控制問題.建立連續LuGre穩態摩擦模型，解決原模型不可微分的缺點，該連續模型可以有效刻畫庫倫摩擦、粘滯摩擦、Stribeck現象等多種摩擦特征.基于該模型提出了含有可變系數的快速終端滑模控制器，該方法既能保證電機快速達到同步，又能完成高精度的跟蹤.仿真結果表明了文中所提方法具有很好的性能.

［1］MUVENGEI O，KIHIU J，IKUA B.Dynamic analysis of planarmulti-body systems with LuGre friction at differently located revolute clearance joints［J］.Multibody System Dynamics，2012，28(4):369－393.

［2］WANG X，WANG S.High performance adaptive control of mechanical servo system with LuGre friction model:identification and compensation［J］.Journal of Dynamic Systems，Measurement and Control，2012，134(1):011021.

［3］HOSHINO D，KAMAMICHI N，ISHIKAWA J.Friction compensation using time variant disturbance observer based on the LuGre model［C］//Proceedings of the 12th IEEE InternationalWorkshop on Advanced Motion Control.Sarajevo:IEEE，2012:1－6.

［4］FREIDOVICH L，ROBERTSSON A，SHIRIAEV A，et al. LuGre-model-based friction compensation ［J］.Control Systems Technology，IEEE Transactions on，2010，18(1):194－200.

［5］向紅標，譚文斌，李醒飛，等.基于LuGre模型的自適應摩擦補償［J］.機械工程學報，2012，48(17):70－74.

［6］WANG X J，LI J Y，WU B，et al.Continuous rotary motor electro-hydraulic servo system based on the zero phase error tracking controller［J］.Applied Mechanics and Materials，2012，121:3205－3209.

［7］LIU Z，LIU B F.Robust Control strategy for the speed control of brushless DC motor［J］.Journal of Harbin Institute of Technology，2013，20(2):90－94.

［8］ZHANG Z，CHAU K T，WANG Z.Chaotic speed synchronization control of multiple induction motors using stator flux regulation［J］.Magnetics，IEEE Transactions on，2012，48(11):4487－4490.

［9］TIAN Y F，GUO Q C，Robustness-tracking control based on sliding mode and H∞theory for linear servo system［J］.Journal of Harbin Institute of Technology，2005，12(2):213－217.

［10］LIU Z L，LIU G Z，LIU J.Neural adaptive sliding mode speed tracking control of a DC motor［J］.Journal of Systems Engineering and Electronics，2004，15(3):304－308.

The fast terminal sliding mode control of dual-motor driving servo systems with friction

ZHAO Wei，REN Xuemei
(School of Automation，Beijing Institute of Technology，100081 Beijing，China)

To solve the non-differentiable problem of original frictionmodel，an exponential function containing speed variables is introduced to design the continuous differentiable LuGre steady-state friction model for dualmotor driving servo systems.The proposed model captures the main characteristics of friction including Stribeck effect，coulomb and viscous friction.Based on the continuous differentiable model，a nonlinear variable coefficient characterizing the synchronization rate is used for fast terminal sliding mode，such that the system is proved to achieve synchronization and tracking control for the reference signal with prescribed performance by Lyapunov function.The simulations are included to verify fast convergence speed and high tracking precision of the proposed algorithm.

dual-motor driving servo systems;fast terminal sliding mode;continuous LuGre friction model;tracking control;synchronization control

TP13

A

0367－6234(2014)03－0119－05

2013－10－23.

國家自然科學基金資助項目(61273150、60974046);高等學校博士學科點專項科研基金資助項目(20121101110029);長江學者和創新團隊發展計劃資助項目(IRT12 08).

趙 威(1986—)，男，博士研究生;

任雪梅(1967—)，女，教授，博士生導師.

任雪梅，xmren@bit.edu.cn.

(編輯 苗秀芝)