壽命服從PH分布的冷貯備可修系統

趙 丹，周 巖，孟憲云，李海霞

（燕山大學理學院，河北秦皇島 066004）

壽命服從PH分布的冷貯備可修系統

趙 丹，周 巖，孟憲云，李海霞

（燕山大學理學院，河北秦皇島 066004）

研究了由兩個不同部件組成的冷貯備系統。假定部件的工作時間服從的是PH分布，且假定部件能夠修復如新，部件失效后的修理時間服從指數分布。利用引進變量法、廣義的馬爾可夫過程和PH分布的性質，得到了系統的瞬時概率分布、系統首次故障前的平均時間、系統穩態概率分布等可靠性指標的Laplace變換表達式。

PH分布；冷貯備；引進變量法；廣義的馬爾可夫過程；可修系統；可靠性

0 引言

在可靠性分析中，常用的貯備系統有溫貯備系統和冷貯備系統，冷貯備系統應用比較廣泛，因此受到學者們的關注。所謂冷貯備就是指部件在貯備過程中既不失效也不劣化，貯備期的長短與部件日后使用時的工作壽命無關，貯備部件替換失效部件是通過轉換開關來完成的。文獻［1］研究了壽命和修理時間服從一般分布的可修系統，文獻［2－3］分別研究了含有兩個同型和不同型部件的冷貯備可修系統，文獻［4］在此基礎上針對帶有優先權的兩不同型部件冷貯備系統進行了可靠性分析，文獻［5］研究了有優先權且有兩不同修理設備的兩部件冷貯備可修系統，文獻［6］研究了修理時間服從PH分布、壽命服從指數分布的兩個不同型部件、一個修理工組成的并聯可修系統，更多關于帶有PH分布的可修系統的可靠性分析可參考文獻［7－9］。本文在以往文獻的研究基礎上，對于修理時間服從指數分布、壽命服從PH分布的兩個不同型部件、一個修理工組成的冷貯備系統進行了討論。

1 模型假設

（Ⅰ）部件1的工作壽命服從的是m階PH分布，其分布函數為G1（t）＝1－αeTte，t≥0，過程的初始概率向量為α＝（α1，α2，…，αm），狀態轉移概率矩陣為T＝（Tij）m×m，且滿足T0＝－Te1＝（，…）′，其中e1為分量全為1的m階列向量。

部件2的工作壽命服從的是n階PH分布，其分布函數為G2（t）＝1－βeRte，t≥0，過程的初始概率向量為β＝（β1，β2，…，βn），狀態轉移概率矩陣為R＝（Rij）n×n，且滿足R0＝－Re2＝（，…，）′，其中e2為分量全為1的n階列向量。

（Ⅱ）部件i故障后的修理時間服從參數為μi的指數分布，其分布函數為Fi（t）＝1－e－μit，t≥0，（μi＞0），i＝1，2。

（Ⅲ）上述所有隨機變量是相互獨立的。

（Ⅳ）在t＝0時刻，部件1先開始工作，部件2貯備，且兩個部件都是完好無損的。轉換開關完全可靠且轉換是瞬時的。當正在工作的部件癱瘓時，貯備部件立即去替換而進入工作狀態，修理工立即修理失效部件；如果兩個部件都壞了，則遵循先壞先修的原則，假定修復如新。

2 主要結果及證明

X（t）＝i表示時刻t系統處于狀態i，i＝0，1，2，3，4，5。由于系統中所假設的部件壽命不服從指數分布，那么可以驗證｛X（t），t≥0｝不是馬氏過程。現在引入補充變量：令Z（t）＝j表示正在工作中的部件在時刻t所處的位相，則｛X（t），Z（t），t≥0｝構成了一個廣義的馬爾可夫過程。此時系統的狀態可有

證明由系統的模型假設可得系統的狀態為

狀態0：部件1開始工作，部件2進入貯備狀態。

狀態1：部件2開始工作，部件1進入貯備狀態。

狀態2：部件1修理，部件2開始工作。

狀態3：部件2修理，部件1開始工作。

狀態4：部件1正在修理，部件2處于待修。

狀態5：部件2正在修理，部件1處于待修。

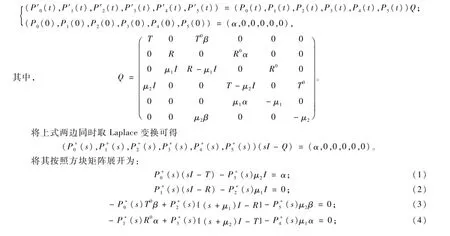
證明由可用度的定義和定理1的結果即可得出結論。

定理2設Z為系統首次失效時間，則Z服從2（m＋n）階PH分布F（t），且可得系統的可靠度函數為R（t）＝P｛Z≥t｝＝γePte，e為分量全為1的2（m＋n）維列向量，且該函數的Lap lace變換為R*（s）＝

證明將上述馬氏過程中的故障狀態（4，5）歸并為一個吸收態N，則狀態空間為j＝｛（0，1），…，（0，m），（1，1），…，（1，n），（2，1），…，（2，n），（3，1），…，（3，m），N｝，對應的轉移概率矩陣為：

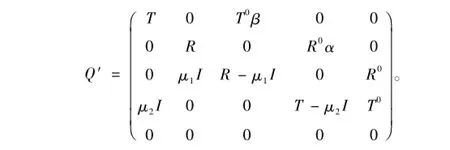
劃去最后一行和最后一列的矩陣為P，其中，P0＝－Pe＝（0，0，R0，T0）T；γ＝（α，0，0，…，0）∈R2（m＋n）；e為分量全為1的2（m＋n）維列向量。則由PH分布的定義可知：系統的首次失效時間Z服從2（m＋n）階PH分布，再由可靠度的定義及Lap lace變換即可得到定理后半部的結論。

定理3設π＝（π0，π1，π2，π3，π4，π5）為系統的平穩概率分布，其中πi是系統處于狀態i的穩態概率，其中，π4，π5∈R＋；π1，π2是n維行向量；π0，π3是m維行向量，則有

證明該隨機過程是一個不可約有限狀態馬氏過程，所以其平穩概率π＝（π0，π1，π2，π3，π4，π5）存在，且滿足方程組

將式（8）按方塊矩陣展開為：

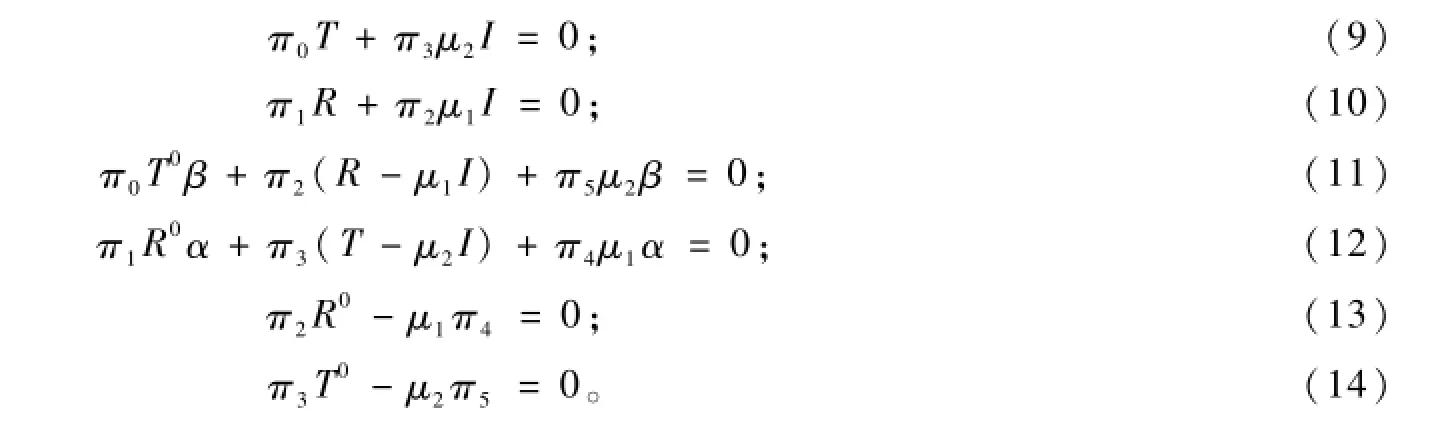
由式（13）和式（14）可得

將式（15）代入式（11）和式（12）化簡得

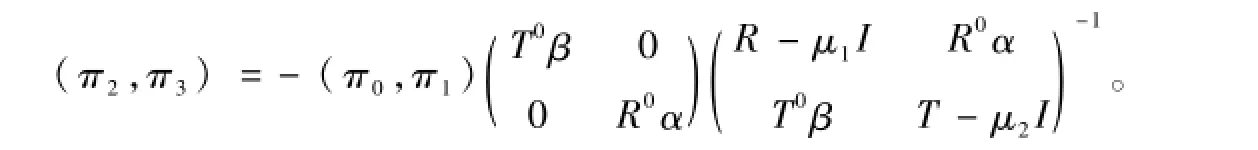
將上式代入式（15）則有

由式（9）、式（10）和式（11）可得

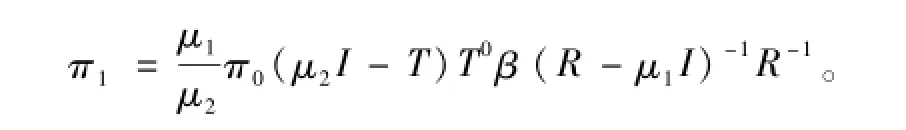
推論2假設系統的穩態可用度為A，則有

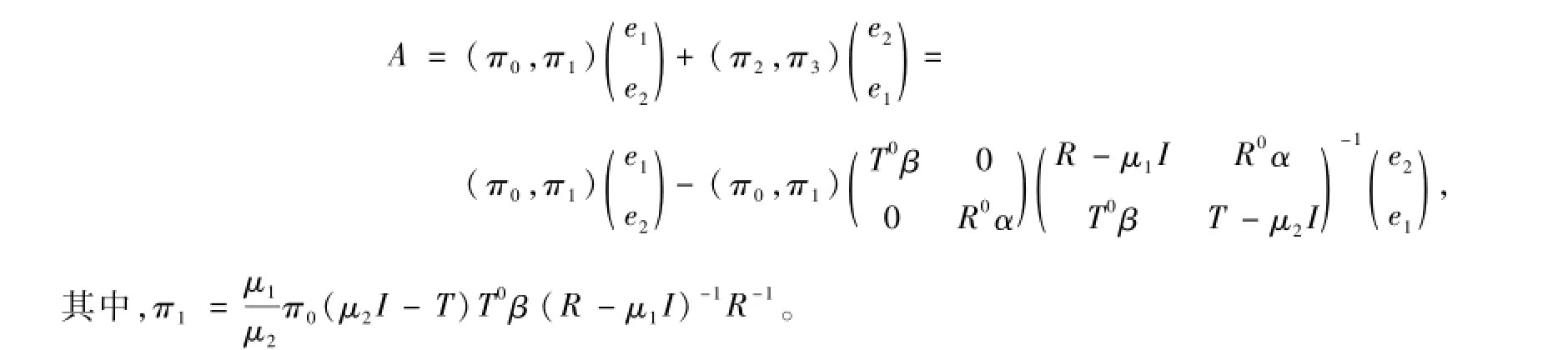
證明由可用度的定義和定理3的結果即可得出結論。

3 結論

本文討論了部件壽命服從PH分布、修理時間服從指數分布的兩不同型部件的冷貯備系統。PH分布是指數分布和幾何分布的矩陣類比，它的參數矩陣具有明顯的概率意義，將之應用于可靠性分析中，可以較易地得到系統的一些主要可靠性指標，所得結果更具有一般性，因此更加具有實際意義。

［1］ 曹晉華，程侃.可靠性數學引論［M］.北京：科學出版社，2006.

［2］ 李才良，蒲冰遠，唐應輝，等.兩不同部件冷貯備系統的可靠性分析［J］.電子科技大學學報，2003，32（4）：447－450.

［3］ 周美秀，范偉峰，胡曉曉.兩相同部件冷貯備可修系統的定性分析［J］.數學的時間與認識，2009，39（18）：50－53.

［4］ 張民悅，包林濤，段紅星.有優先權的兩個不同型部件冷貯備可修系統［J］.蘭州理工大學學報，2007，33（2）：152－155.

［5］ 賈鵬茹，孟憲云，張曉爽，等.有優先權且有兩不同修理設備的兩部件冷貯備可修系統的可靠性分析［J］.數學的實踐與認識，2010，4（10）：187－192.

［6］ 董兵，唐應輝.修理時間服從PH分布的兩部件可靠性分析［J］.西華大學學報，2008，27（3）：69－71，76.

［7］ 岳德權，李蘭巧，祁洪娟.PH／M／c可修排隊系統［J］.數學的實踐與認識，2010，40（8）：132－137.

［8］ Delia M C，Rafael P O.A Deteriorating Two-system with Two Repair Modes and Sojourn Times Phase-type Distributed［J］.Reliability Engineering and System Safety，2006，91：1－9.

［9］ Juan E R C，Rafael P O，Gemma F V.Modelling a Reliability System Governed by Discrete Phase-type Distributions［J］. Reliability Engineering and System Safety，2008，93：1650－1657.

O213.2

A

1672－6871（2014）01－0092－05

全國統計科研計劃基金項目（2010LC33）；河北省教育廳計劃基金項目（2007323）

趙 丹（1986－），女，黑龍江鶴崗人，碩士生；周 巖（1964－），男，黑龍江齊齊哈爾人，副教授，碩士生導師，研究方向為系統的可靠性分析及優化.

2012－04－20