1-丁烯/聚1-丁烯溶液體系黏度的測量及建模

沈周峰，王金剛，于魯強，陳江波，畢福勇，杜亞鋒

（中國石化 北京化工研究院，北京 100013）

1-丁烯/聚1-丁烯溶液體系黏度的測量及建模

沈周峰，王金剛，于魯強，陳江波，畢福勇，杜亞鋒

（中國石化 北京化工研究院，北京 100013）

測定了1-丁烯/聚1-丁烯溶液體系在不同的固含率（C，%（w））、溫度（t，℃）和剪切速率（γ，s-1）下的黏度（η，Pa·s），并對測定的黏度數據進行擬合。實驗結果表明，1-丁烯/聚1-丁烯溶液體系的黏度隨溫度的升高而降低，隨剪切速率的增大而降低，隨固含率的增大而增大。在10 s-1＜γ＜500 s-1、70 ℃≤t≤130 ℃、2.5%≤C≤25.0%的條件下，將1-丁烯/聚1-丁烯溶液體系測定的黏度數據經擬合得到恒壓黏度模型：η = 2.543×10-4γ.-0.3611×exp[1 625.53/(t + 273)]×exp(12.76C)。該黏度模型的方差齊性檢驗值為17 314.02、結果可信度值為0、調整相關系數平方為0.946 8，對實驗數據擬合較好。

聚1-丁烯；1-丁烯；黏度模型

聚1-丁烯具有良好的耐溫性、化學穩定性、耐磨性和可塑性，它無味、無毒、無嗅，可與其他聚烯烴共混生產各種不同特性的聚烯烴塑料產品，擴大了聚烯烴塑料制品的品種和應用范圍。自20世紀60年代Ziegler-Natta催化劑出現后，國內外對1-丁烯的聚合開展了大量研究。目前，高全同（全同結構含量不小于96%（w））、高結晶度（50%～60%）的聚1-丁烯塑料已實現工業化生產［1-4］。聚1-丁烯的主要生產方法為本體聚合［5-7］，但有關1-丁烯/聚1-丁烯溶液體系的相關基礎研究報道較少。

本工作測定了1-丁烯/聚1-丁烯溶液體系在不同的固含率、溫度和剪切速率下的黏度，并對實驗測定的黏度數據進行擬合，建立了1-丁烯/聚1-丁烯溶液體系的黏度與固含率、溫度和剪切速率之間關系的函數模型，為1-丁烯本體聚合的工藝設計提供參考。

1 黏度模型

1-丁烯/聚1-丁烯溶液體系為假塑性流體［8］，其流變特性可用指數函數方程（見式（1））描述［9］。

式中，τ為剪切應力，Pa；γ為剪切速率，s-1；n為流動行為指數；k為稠度指數。

為便于計算，將式（1）簡化為式（2）。

式中，η為黏度，Pa·s。

Harper等［10］經過統計分析，提出如式（3）的經驗式。

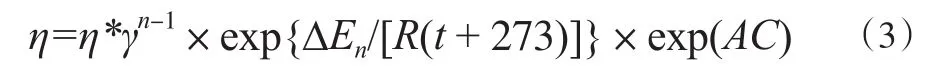
式中，η*為表觀黏度，Pa·s；ΔEn為流動活化能，J；R=8.314，氣體常數；t為溫度，℃；C為固含率（w），%；A為常數。

式（3）雖得到廣泛應用，但它并不適用于γ的全部值域。當γ→0時，η→η0；當γ→∞時，η→η∞，且η0和η∞都是非零且有限的。因此式（3）只對γ的中等值域適用。

可利用Oldroyd方程［11］建立修正模型［12］，得到式（4）。

式中，η0，a1，a2均為正的常數。

對于式（4），當γ→0時，η→η0；當γ→∞時，η→η0a1/a2。對于假塑性流體，a1＜a2；對于膨脹性流體，a1＞a2；對于牛頓流體，a1=a2=0。所以，式（4）能較好地在全值域描述流體黏度，但它比式（3）復雜，會給待定參數的擬合帶來困難。

本工作選擇的γ范圍基本在式（3）允許的范圍內，故根據實際情況可選用式（3）作為黏度模型進行數據擬合。如最后的擬合結果不能滿足黏度描述的要求，可再考慮用式（4）進行修正。式（3）可轉化為相對簡單的多項式（見式（5））以易于進行函數擬合。

式中，y=lnη，k0=lnη*，k1=n-1，k2=ΔEn/R，k3=A，z1=lnγ，z2=1/（t+273），z3=C。

2 實驗部分

2.1 試劑與儀器

聚1-丁烯：牌號PB4235，荷蘭巴塞爾公司；1-丁烯：聚合級，天津化工廠，經脫氧、脫水處理后使用。

HAAKE RS6000型旋轉流變儀：美國Thermo Fisher Scientifc公司。

2.2 實驗方法

1-丁烯/聚丁烯-1溶液體系黏度的測定裝置見圖1。測試方法為：向反應釜中加入一定量的聚1-丁烯和1-丁烯，升溫至90 ℃，加熱并攪拌2 h左右直至1-丁烯/聚1-丁烯充分溶解。打開旋轉流變儀，升溫至70 ℃，預熱10 min以上。打開反應釜底部與旋轉流變儀之間的連接閥，將1-丁烯/聚1-丁烯溶液利用釜內自身壓力壓入流變儀中，然后關閉連接閥。啟動旋轉流變儀，設定一定剪切速率進行預剪切使溶液混合均勻，開始測定黏度。

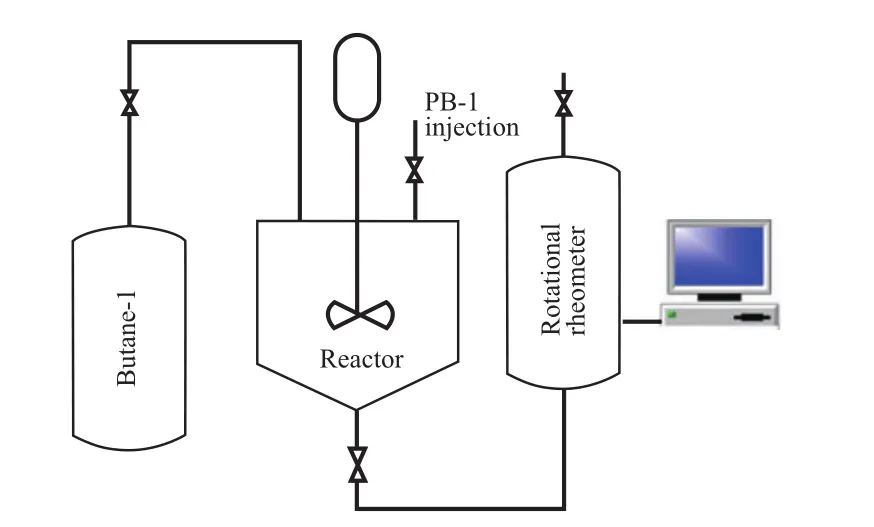
圖1 1-丁烯/聚1-丁烯溶液體系黏度的測定裝置Fig.1 Device for measuring the viscosity of butane-1/polybutylene-1（PB-1） solution.

3 結果與討論

3.1 黏度的影響因素

分別測定了1-丁烯/聚1-丁烯溶液體系在不同的固含率、溫度和剪切速率下的黏度。固含率為10%和20%的1-丁烯/聚1-丁烯溶液體系的黏度-剪切速率曲線分別見圖2和圖3。從圖2～3可看出，當固含率相同時，1-丁烯/聚1-丁烯溶液體系的黏度隨溫度的升高而降低，隨剪切速率的增大而降低。

1-丁烯/聚1-丁烯溶液體系的黏度-固含量曲線見圖4。由圖4可看出，當溫度和剪切速率相同時，1-丁烯/聚1-丁烯溶液體系的黏度隨固含率的增大而增大。

3.2 黏度模型的擬合

將1-丁烯/聚1-丁烯溶液體系在不同的固含率、溫度和剪切速率下測定的黏度數據按式（5）進行換算。其中，固含率為10%（w）的1-丁烯/聚1-丁烯溶液體系在70 ℃下測定的黏度數據的換算見表1。

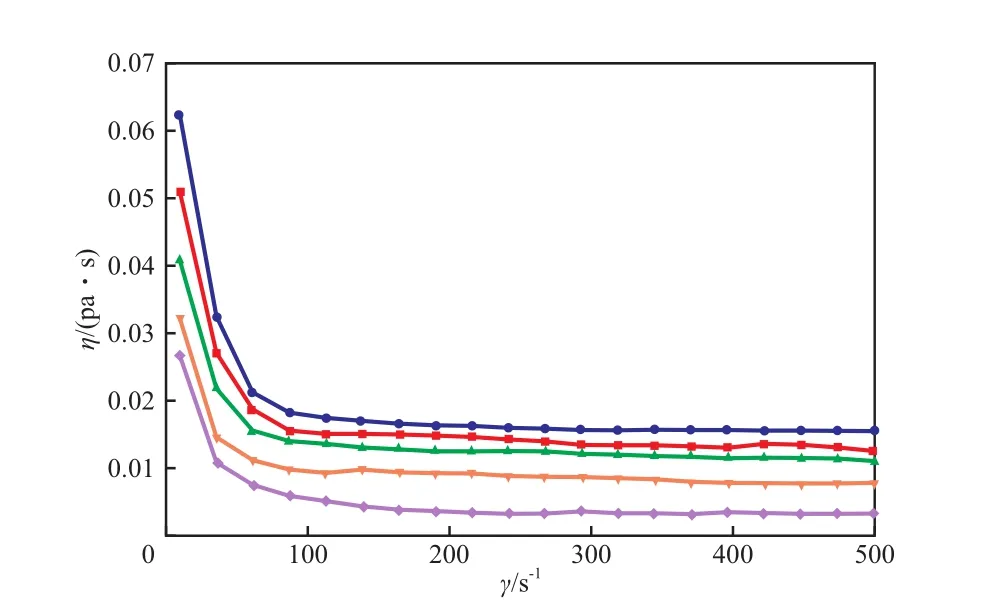
圖2 固含率為10%的1-丁烯/聚1-丁烯溶液體系的黏度-剪切速率曲線Fig.2 Viscosity（η）-shear rate（γ） curves of butane-1/PB-1 solution system with solid content of 10%（w）.

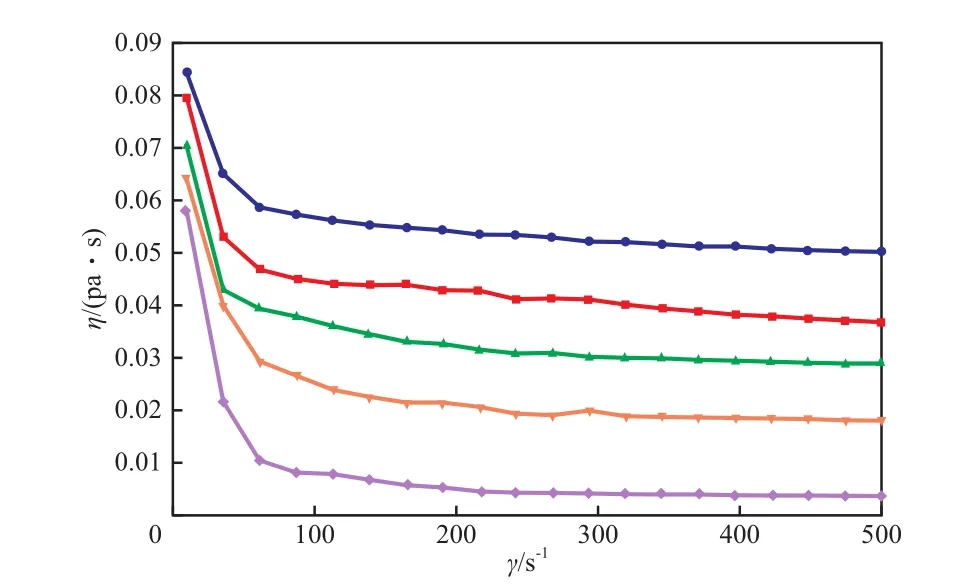
圖3 固含率為20%的1-丁烯/聚1-丁烯溶液體系的黏度-剪切速率曲線Fig.3 η-γ curves of butane-1/PB-1 solution system withsolid content of 20%（w）.

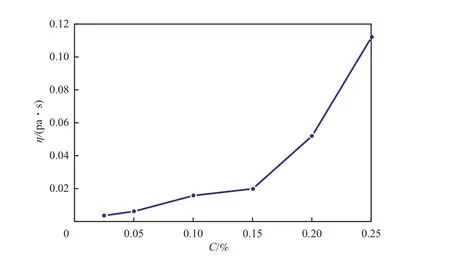
圖4 1-丁烯/聚1-丁烯溶液體系的黏度-固含量曲線Fig.4 η-solid content（C） curve of butane-1/PB-1 solution systems.

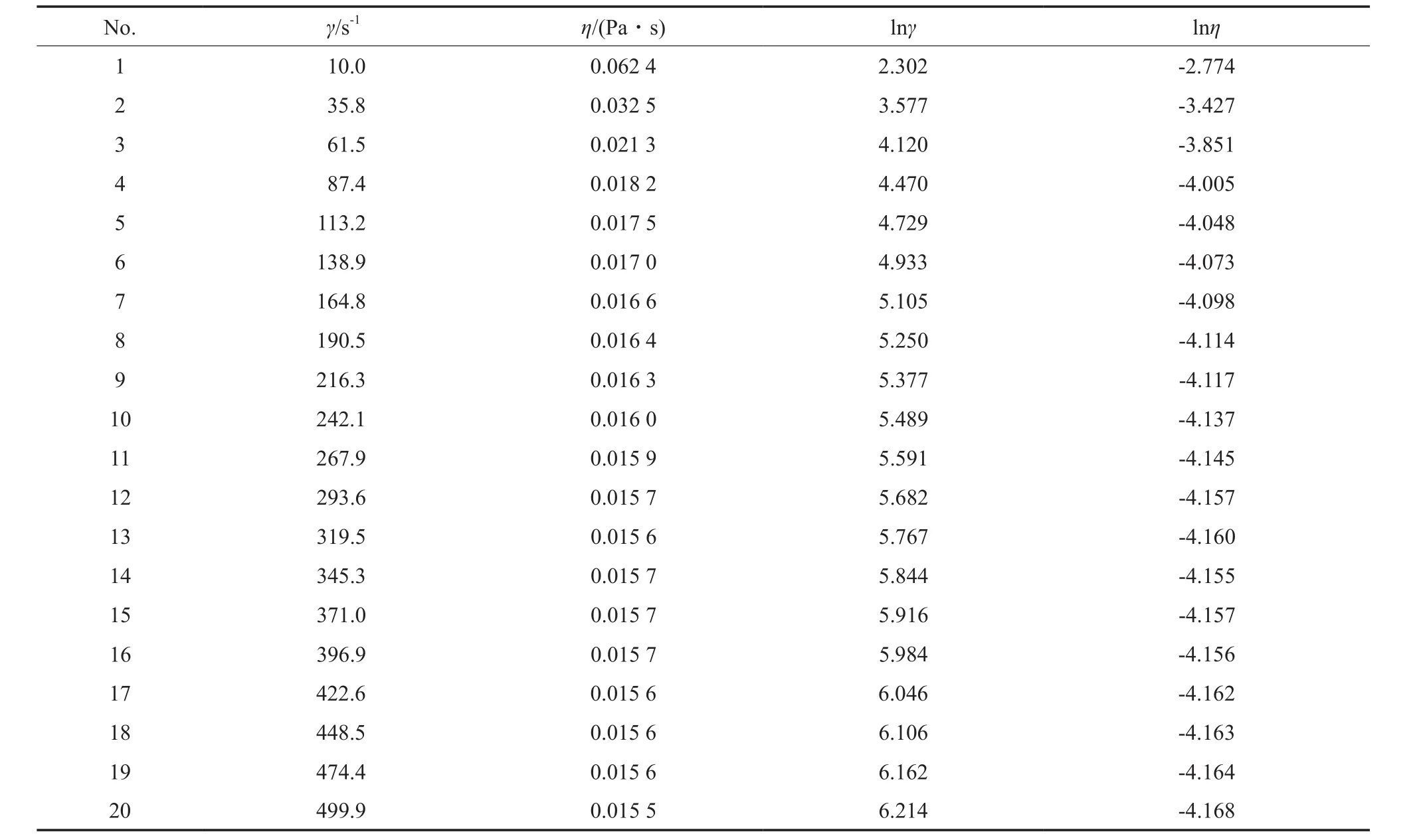
表1 1-丁烯/聚1-丁烯溶液體系黏度測定實驗數據的換算Table1 Experimental results for measuring the viscosity of the butane-1/PB-1 solution systems

1-丁烯/聚1-丁烯溶液體系在溫度高于146.4℃、壓力大于4.05 MPa時為超臨界狀態，因此150℃時，1-丁烯/聚1-丁烯溶液體系已處于超臨界狀態，黏度會發生較大突變，故在黏度模型擬合時不考慮150 ℃的數據。

將1-丁烯/聚1-丁烯溶液體系在不同溫度下測定的黏度數據經擬合計算，得到回歸方程（見式（6））。

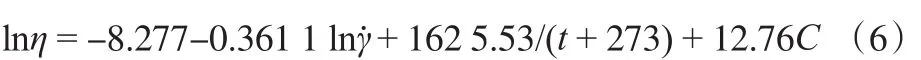
計算結果表明，式（6）的調整相關系數平方R2=0.946 8，說明該回歸方程的擬合度很好。方差齊性檢驗（F）值為17 314.02，；結果可信度（P）值為0（P值越小可信度越高），說明該回歸方程的相關性極其顯著。因此，用式（3）描述黏度隨固含率、溫度和剪切速率的變化規律是適用的。

再將式（6）變換為式（3）的形式，可得恒壓黏度模型（見式（7））。

式中，10 s-1＜γ＜500 s-1，70 ℃≤t≤130 ℃，2.5%≤C≤25%。

以1 625.53/（t+273）+12.76C為橫坐標（X），lnη+8.277+0.361 1lnγ為縱坐標（Y）做圖，線性回歸結果見圖5。由圖5可看出，所得曲線Y=X為直線，說明黏度模型對實驗中測定的黏度數據擬合較好。

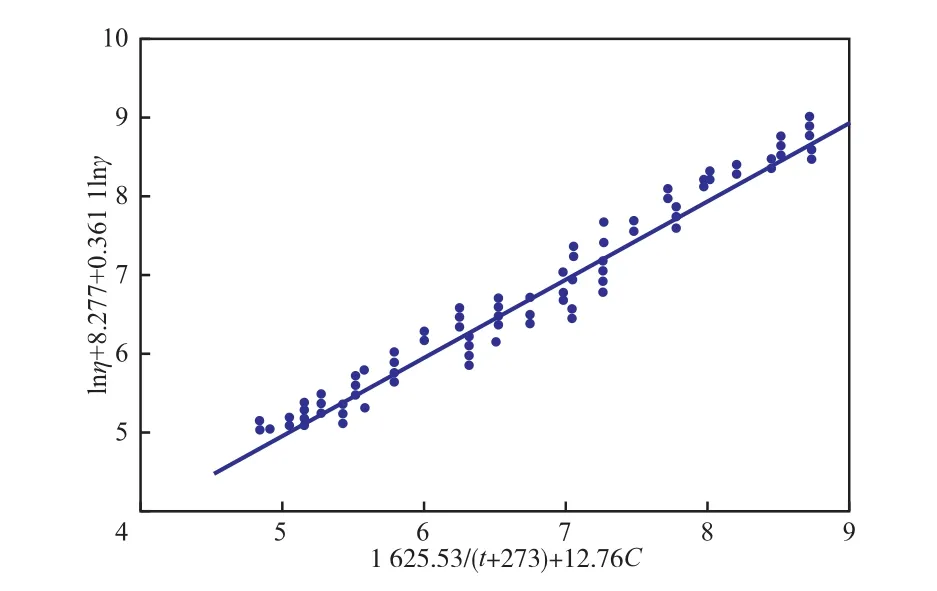
圖5 黏度模型的線性回歸圖Fig.5 Linear regression by the viscosity model.

4 結論

1）1-丁烯/聚1-丁烯溶液體系的黏度隨溫度的升高而降低，隨剪切速率的增大而降低，隨固含率的增大而升高。

2）在10 s-1＜γ＜500 s-1、70 ℃≤t≤130 ℃、2.5%≤C≤25%的條件下，將1-丁烯/聚1-丁烯溶液體系測定的黏度數據經擬合得到恒壓黏度模型：η=2.543×10-4γ.-0.3611×exp [1 625.53/(t+273)]×exp (12.76C)。該黏度模型的F=17 314.02、P=0、 R2=0.946 8，對實驗數據的擬合較好。

［1］ 楊曉瑩，白玉潔，王秀繪. 聚丁烯-1技術研究進展［J］. 化工中間體，2012，9（6）：5 - 8.

［2］ 楊金興，喬輝，史翎. 國內外聚丁烯-1的研究進展［J］. 塑料，2013，42（3）：47 - 50.

［3］ 彭嘉冠，孫研. 全材料聚丁烯-1的性能及應用［J］. 河南化工，2010，27（1）：17 - 19.

［4］ 馮濤，邵華鋒，姚薇，等. 不同聚合方法合成聚1-丁烯熱塑性彈性體的結構和性能［J］. 合成橡膠工業，2009，32（1）：26 - 28.

［5］ 盛海波，王波，姚薇，等. 負載鈦催化丁烯-1本體聚合研究［J］. 彈性體，2005，15（3）：21 - 23.

［6］ Azzurri F，Gmez M A，Alfonso G C，et al. Time-Resolved SAXS/WAXS Studies of the Polymorphic Transformation of 1-Butene/Ethylene Copolymers［J］. J Macro Mol Sci，2004，B43（1）：177 - 189.

［7］ Abedi S，Sharifi-Sanjani N. Preparation of High Isotactic Polybutene-1［J］. J Appl Polym Sci，2000，78（14）：2533 -2539.

［8］ Song Yuhua，Mathias P M，Tremblay D，et al. Liquid Viscosity Model for Polymer Solutions and Mixtures［J］. Ind Eng Chem Res，2003，42（11），2415 - 2422.

［9］ 王凱，孫建中. 工業聚合反應裝置［M］. 北京：中國石化出版社，1997：1 - 30.

［10］ Harper J M. Extrusion of Food （Volume 1）［M］. Florida：CRC Press Ico，1981：41 - 46.

［11］ 陳文芳. 非牛頓流體力學［M］.北京：科學出版社，1984：112 - 117.

［12］ 馬海樂. 大豆面團粘度模型的研究［J］. 江蘇理工大學學報：自然科學版，2001，22（2）：34 - 37.

（編輯 鄧曉音）

Measurement and Modeling of Butene-1/Polybutylene-1 Solution Viscosity

Shen Zhoufeng，Wang Jingang，Yu Luqiang，Chen Jiangbo，Bi Fuyong，Du Yafeng
（SINOPEC Beijing Research Institute of Chemical Industry，Beijing 100013，China）

The viscosity（η） of butane-1/polybutylene-1 solutions with different solid content（C）at different temperature（t） and shear rate（γ） was measured and a viscosity model was established. The results indicated that the viscosity of the butane-1/polybutylene-1 solutions decreased with temperature rise，decreased with increasing shear rate and increased with increasing solid content. Under the condition of 10 s-1＜γ＜500 s-1，70 ℃≤t≤130 ℃ and 2.5%≤C≤25%，the constant pressure viscosity model for the butane-1/polybutylene-1 solutions was η = 2.543×10-4γ.-0.3611×exp [1 625.53/(t + 273)]×exp(12.76C)with homoscedasticity test value of 17 314.02，confdence level of 0 and correlation coeffcient square of 0.946 8.

polybutylene-1；1-butene； viscosity model

1000 - 8144（2014）12 - 1401 - 04

TQ 325.15

A

2014 - 06 - 09；［修改稿日期］ 2014 - 09 - 21。

沈周峰（1987—），男，浙江省嘉興市人，碩士，電話 18758805807，電郵 670779301@qq.com。聯系人：于魯強，電話 010 - 59202618，電郵 yulq.bjhy@sinopec.com。