基于復雜網絡的時間序列雙變量聯動波動

安海崗

（石家莊經濟學院管理科學與工程學院，石家莊 050031）

基于復雜網絡的時間序列雙變量聯動波動

安海崗

（石家莊經濟學院管理科學與工程學院，石家莊 050031）

選擇倫敦金與Au9999下午收盤價格作為樣本數據研究時間序列雙變量之間的聯動波動規律.依據粗粒化方法，將倫敦金與Au9999價格的聯動波動狀態轉化為由5個｛P，N，M｝字符組成的字符串，每個字符串代表5天的價格聯動波動模態.將模態作為節點，模態之間的轉化為邊，構建價格聯動波動復雜網絡.運用復雜網絡理論對時間序列雙變量聯動波動模態的統計、變化規律和演化機制進行分析.結果表明：時間序列雙變量聯動波動模態分布具有冪律性、群簇性和周期性，其聯動波動模態主要通過少數幾種模態進行轉換與演化.本方法不僅可以研究不同類型時間序列雙變量聯動波動，同時可為多變量聯動波動研究提供思路.

復雜網絡；粗粒化；聯動波動；時間序列

0 引言

時間序列數據是一種動態的高維數據，與靜態數據不同之處在于它是隨著時間的改變而發生變化.在金融、經濟及工程管理等眾多領域，通過對時間序列數據進行挖掘與分析能夠為管理者提供許多有價值的商業信息，為管理決策制定提供參考［1］.挖掘時間序列數據中的各種動態特征及發展演化規律，是一種重要的統計分析方法，廣泛應用于自然科學、社會科學等領域，是一種科學研究的創新性思維.時間序列數據是一種歷史數據，通過對歷史數據進行統計分析，可預測其未來發展趨勢，即時間序列數據預測.

時間序列數據預測包括單變量預測和多變量預測兩種.在目前單變量時間序列預測方法中，常用的有移動平均與分解方法［2］、指數平滑方法［3］、Box-Jenkins方法［4］、ARARMA模型［5］、Pandit-Wu方法［6］、干預分析模型［7］、狀態空間模型及Bayesi-an預測方法［8］等.倫敦金與Au9999現貨黃金價格屬于時間序列雙變量，對時間序列雙變量之間關系進行研究的傳統方法主要側重于探究它們之間的均衡關系，包括自回歸模型［9］、協整檢驗及誤差修正模型、方差分析［10］、數據挖掘［11］、多元統計［12］、協同理論［13］等.倫敦金與Au9999每天都在發生著變化，兩種價格的聯動性也隨之發生著改變，它們之間的聯動關系是一個非線性的、動態變化的復雜系統.現有的傳統經濟學中的方法很難揭示關系的波動機理，而物理經濟領域的研究為我們提供了一些新的思路和方法.對于此類問題，國內外學者將粗粒化方法與復雜網絡理論結合起來進行了一些研究，包括對我國溫度波動模態的分析［14］、國際原油價格波動的分析［15］、國際原油與國內原油價格波動關系的研究［16］等.

黃金具有貨幣和商品的雙重屬性，是各國外匯儲備的重要組成部分，具有良好的流通性和不可替代的保值與避險功能，一直受到各國政府的重視.近些年來，由于中國黃金市場的發展和中國影響力的不斷增大，中國黃金市場正日益受到國際社會的關注，在國際黃金市場上的影響力也在逐年提高，但中國黃金市場在國際黃金定價中的影響力究竟有多大，與國際黃金市場之間存在怎樣的聯系以及這種聯系的動態特征，是多數投資人與管理者關注的問題.

由以上研究可知，國際倫敦金與我國的Au9999黃金現貨價格的時間序列雙變量之間存在聯動性，通過傳統的經濟方法可以將雙變量之間的關系表示出來，但是對于雙變量之間是如何聯動波動的，以及內在的變化規律和演化機理卻無法描述.要解決該問題可以借鑒統計物理學的方法，將復雜網絡理論與粗粒化方法應用于其聯動波動的研究中來.本文運用粗粒化方法將倫敦金與Au9999黃金現貨價格的聯動波動關系轉換為聯動波動模態，以時間順序關系為邊構建復雜網絡模型，并運用復雜網絡理論對其聯動波動復雜網絡進行統計分析，進而研究其內在的變化規律和演化機理.

1 數據與方法

1.1 數據

本文的研究需選擇兩個時間序列單變量作為研究對象，且此變量應具有一定代表性，因此選擇上海黃金交易所Au9999黃金現貨收盤價與倫敦標準黃金現貨的下午定盤價作為樣本數據.上海黃金交易所黃金現貨價格是我國黃金現貨價格的晴雨表，倫敦標準金代表國際黃金現貨的黃金價格.倫敦標準黃金現貨為純度不低于99.5%的標準金塊，而上海黃金交易所的Au9999為純度在99.99%以上的Au9999金，是上海黃金交易所交易時間最長且交易量較大的一種黃金現貨，二者在品質上具有一致性［17］.

選取2003年1月1日到2013年9月6日之間的黃金價格數據.由于國內外市場節假日不同，為使數據保持一致，刪除所有的不匹配數據，得到配對數據2553個.由于上海黃金交易所黃金報價單位為人民幣元／克，倫敦黃金報價單位為美元／盎司，因此需對Au9999現貨價格進行標準化處理，其中1盎司＝31.103 5克，匯率采用國家外匯管理局網站統計數據庫中提供的人民幣基準匯價.

1.2 數據粗粒化處理

選取倫敦標準黃金現貨與AU9999的下午定盤價時間序列數據作為研究對象，對于此類經濟金融學數據，價格波動扮演著十分重要的角色.

設AUt為第t天的Au9999現貨價格，LDt為第t天的倫敦標準金現貨價格，AUt－1和LDt－1為第t－1天的Au9999與倫敦金價格，則ΔAU＝AUt-AUt－1，ΔLD＝LDt-LDt－1．當ΔAU×ΔLD＞0時，表示兩者之間具有同向聯動性；當ΔAU×ΔLD＜0時，表示兩者之間具有異向聯動性；當ΔAU×ΔLD＝0時，表示兩者之間價格沒有聯動性［18］.

為了更有效地分析它們之間的聯動性，所選擇的模態符號應越少越好.因此，設兩個價格之間的聯動性為符號CLi，即ΔAU×ΔLD

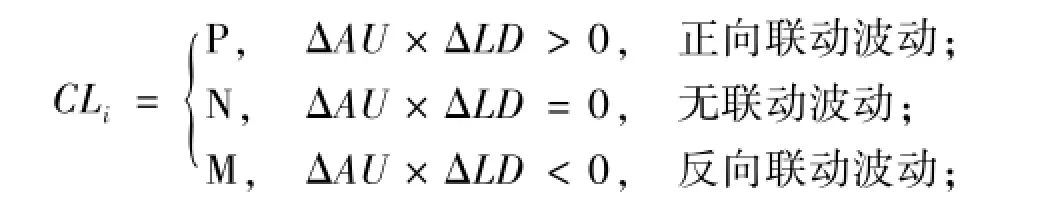
由此，可將雙變量之間聯動波動情況用連續的符號序列來表示，使得對粗粒化的符號序列等同于對時間序列數據的研究.轉化后相應的符號序列CLt為

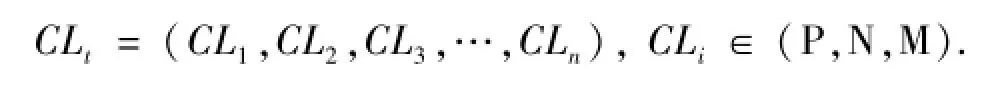
在對2 521－1個聯動波動符號化后，將得到同樣數量的抽象符號序列CLi＝（CL1，CL2，CL3，CL4，CL5，…，CLn）（n＝2 520）．同樣以5個聯動波動符號作為一個符號序列，以1天為步長作數據滑動，由此將得到2 516個價格聯動波動模態.例如本文所構建的黃金價格聯動波動符號序列為：｛MPPMPMMPMPPMMPPNP PPPPPPPPMMP…｝對此字符串做數據滑窗，形成的模態集合｛MPPMP，PPMPM，PMPMM，MPMMP，PMMPM，MMPMP，MPMPP，PMPPM，MPPMM，PPMMP，PMMPP，MMPPN，MPPNP，PPNPP，PNPPP，NPPPP，PPPPP，PPPPP，PPPPP，PPPPP，PPPPP，PPPPM，PPPMM，PPMMP，…｝.由于模態形成過程是通過數據滑動的形式實現的，因此后一個模態的形成以前一個模態為基礎，模態之間具有了傳遞性與有向性，便于模態復雜網絡的構建.整體數據滑動及模態形成過程如表1所示.

1.3 聯動波動復雜網絡分析方法

復雜網絡分析方法主要用來解釋系統中各個要素（即各個模態）之間的分布特征及相互關系，所以應首先構建時間序列雙變量聯動波動復雜網絡模型.復雜網絡由節點與邊構成，本文構建復雜網絡模型時以時間序列雙變量聯動波動模態為節點，模態之間的有向轉換為邊，由此構建復雜網絡.雙變量時間序列聯動波動是一個有向加權網絡，模態間轉換的次數為此有向加權網絡的權重.

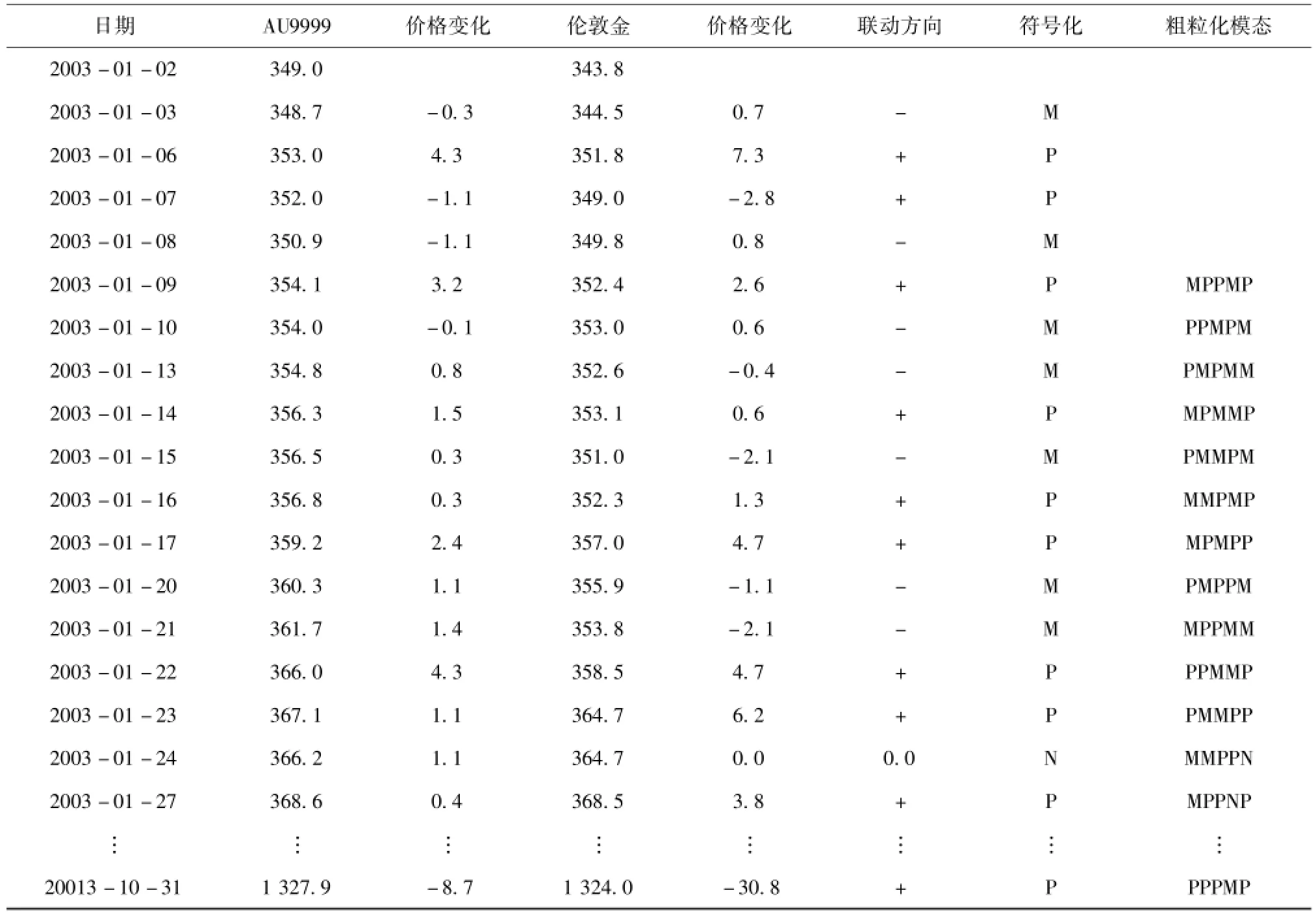
表1 聯動波動粗粒化處理過程Table 1 Coarse-grained process of linkage fluctuation

復雜網絡包括許多統計參數，如度、點強度、平均最短路徑、中心性、加權集聚系數、小團體及結構洞等.通過對這些參數進行分析可對時間序列雙變量聯動波動情況、變化規律與演化機理有所掌握，可對其未來演變趨勢進行預測，為規避市場風險投資提供決策與建議.

1）聯動波動模態的統計規律

聯動波動模態統計規律是對聯動波動模態間復雜關系的統計.本文所構建的倫敦金與Au9999時間序列雙變量聯動波動復雜網絡屬有向加權網絡，與無權網絡不同，加權網絡的邊帶有權重，因此采用點強度的概念，點強度對應無權網絡的度.點強度是該節點在此網絡中重要性的體現，它不僅考慮與該節點連接的所有近鄰，而且還考慮鄰近節點與其之間關聯的緊密，即它們之間的權重.點強度的定義為［19］

式（1）中，Ni為與節點i相連接的由節點i指向的所有近鄰節點的集合，Wij為節點i到j的權重.點強度越大，表明該模態在復雜網絡中的地位越重要，該模態向其他模態轉換的次數越多.

不同節點的點強度不一樣，強度分布存在差異性，本文將時間序列雙變量聯動波動復雜網絡點強度分布定義為

式（2）中ki代表節點i的點強度，N代表所有節點強度的和.

時間序列雙變量聯動波動復雜網絡的點強度及強度分布描述了雙變量之間聯動波動模態及其之間的關聯程度.節點的點強度及強度分布越大表明當前模態向其他模態轉換的次數越多，在網絡中出現的概率也就越大，此模態也就越重要.

2）聯動波動模態的變化規律

聯動波動模態變化規律主要用來研究那些模態在網絡中處于重要位置，這些模態之間怎樣轉換，模態轉換中的核心模態有那些，那些節點控制著網絡的交往能力，在網絡中存在多少個網絡子群.

對子群進行分析時可主要采用n-Cliques方法和k-Plex方法.n-Cliques方法主要對網絡的可達性進行分析，k-Plex方法是基于節點度基礎上子群的一種分析方法.對于一個網絡圖來說，如果存在這樣一個子圖，則可稱它為n－派系：在網絡子圖中，該子圖中的任何兩點之間的最短距離不超過n［20］.令d（i，j）代表節點i和節點j之間的距離，則d（i，j）≤n，將滿足該條件的所有節點組成的子圖即為n-Cliques.k-Plex即滿足以下條件的凝集子群：假如子群中有n個節點，子群中的每個節點都至少與n-k個節點直接有邊相連，即該子群中的每個節點度數都大于或等于n-k［21］.

運用n-Cliques方法和k-Plex方法可對網絡中的凝集子群進行分析，可以解決該復雜網絡中那些模態存在著較多的相互轉換，但是對于模態轉換中的核心模態及不同模態的重要性進行挖掘還需要對其集聚系數進行研究.加權聚集系數為有向復雜網絡中表示網絡節點近鄰之間聚集性質的一個統計參數，聚集系數越高，表示近鄰之間的關聯程度越緊密，反之越松散.倫敦金與Au9999聯動波動復雜網絡就屬于加權復雜網絡，權重表示兩個節點之間關系的緊密程度，權重越大，關系越緊密.本文將加權聚集系數定義為［22］

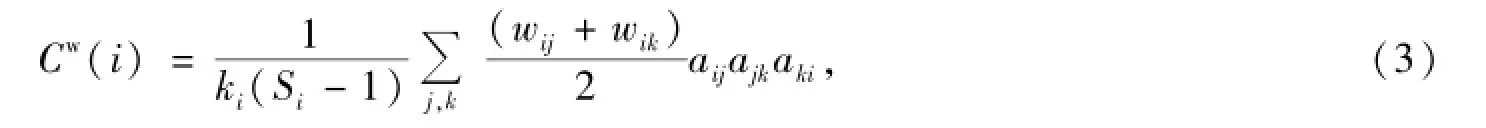
式（3）中，wij代表節點（i，j）邊的權重，ki代表節點i的點強度，Si代表節點i的度數．aijajkaki代表三個節點之間是否相互有關聯，值為0表示它們之間沒有關聯，值1表示它們之間有邊相關聯，如果三者之間均有關聯，表示它們構成一個三角形.加權聚集系數值越高，代表該模態在子群中位置越重要，該模態與其他模態轉換越頻繁越緊密.

3）聯動波動模態的演化規律

聯動波動模態演化規律主要研究不同模態隨時間演化情況，聯動波動模態是通過哪些模態進行轉化的，轉化周期是多少.聯動波動模態演化規律可借助中介中心性和平均路徑長度來統計分析.

對于節點控制能力的分析，可對網絡的中介中心性進行分析.節點中介中心性wk的定義如下：設c（i，j）是節點i與j之間所有最短路徑的總數，路徑的長度就是路徑通過的各條邊的權重，這些路徑中通過中間節點k的路徑數為ck，則節點k的中介中心性測度wk為所有節點對wk（i，j）的和［23］.

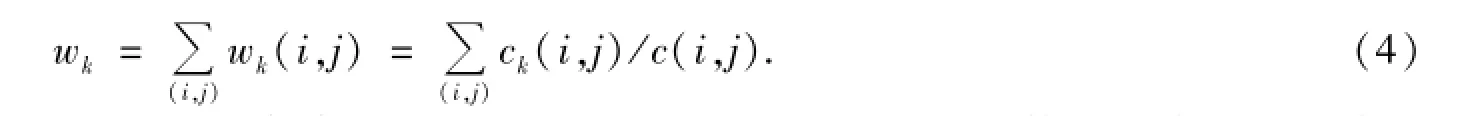
假如兩個節點i和j之間的距離為dij（即任意兩個節點相互連接所要經過的連邊數），網絡的平均路徑長度定義為任意兩個節點之間距離的平均值.在有向網絡中，網絡的平均路徑長度定義為：其中N為網絡中的節點數目.

2 結果及分析

2.1 聯動波動模態統計規律

本文對雙時間序列雙變量倫敦金與Au9999下午定盤價聯動波動模態點強度及強度分布進行了統計計算，對其模態作了粗粒化處理，得到了聯動波動的符號序列.由此符號序列組成的聯動波動模態理論上存在35＝243種，但是實際只出現了106個，其它模態并沒有出現.對符號序列中不同符號出現的次數進行統計后，發現代表正向聯動波動的符號P出現了1 668次，占比66%，代表異向聯動波動的符號M出現了819次，占比32%，代表無聯動波動的符號N僅出現了45次，占比僅2%.這說明在2003年到2013年間，倫敦金與Au9999價格聯動性較強，這與事實一致，結果如圖1所示.

對雙變量聯動波動模態節點強度及強度分布進行統計計算，結果如表2所示.

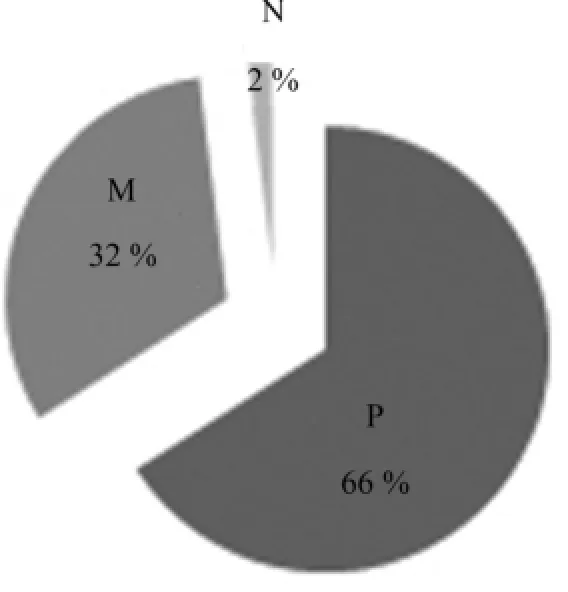
圖1 聯動波動符號出現次數比重Fig.1 Proportion of P，M，N

由表2可知，代表倫敦金與Au9999連續5天同向聯動的字符PPPPP點強度為336，代表連續5天異向聯動的字符MMMMM點強度為17，這說明在這十年多內，倫敦金與Au9999連續5天同向變化共出現了336次，而連續5天異向變化出現次數較少，只有17次，倫敦金與Au9999價格同向聯動性較強.在點強度最高的32個節點中，字符“N”出現次數為零次，這表明在近10年的黃金現貨市場中，黃金現貨價格波動激烈，兩者之間連動性較強.兩者之間的聯動方向性，可通過對加權次數M的計算來獲得.M可定義為價格波動符號出現的次數與該節點的強度分布（即加權次數的權重）的乘積.

在節點度數最高的32個節點中，其聯動性符號組合加權次數如表3所示.由表3可知，隨著同向與反向符號數量的增多，同向符號組合除以反向符號組合的數值越來越大，這表明在黃金現貨聯動波動網絡中，隨著時間的逐步推移，同向聯動性出現的比率越來越多，價格同增或同長頻率越來越高.

在106個節點中，點強度排名前32的節點強度分布占比92.15%，這32個模態向其他模態轉變、或者其他模態向此32個模態轉換概率相對較高.節點強度分布在0.2%以下的節點個數為63，這些節點在此復雜網絡中出現概率較小.

時間序列雙變量倫敦金與Au9999價格聯動波動復雜網絡節點強度k與累積強度LP（k）分布關系如圖2所示.

對聯動波動復雜網絡節點的點強度由高到低排序可得到各個節點的排序名詞，并計算點強度與排序名詞的對數，得到線性回歸方程Y＝－1.751 8＋3.528，回歸系數為0.901，發現它們整體上也服從冪律分布，結果如圖3所示.

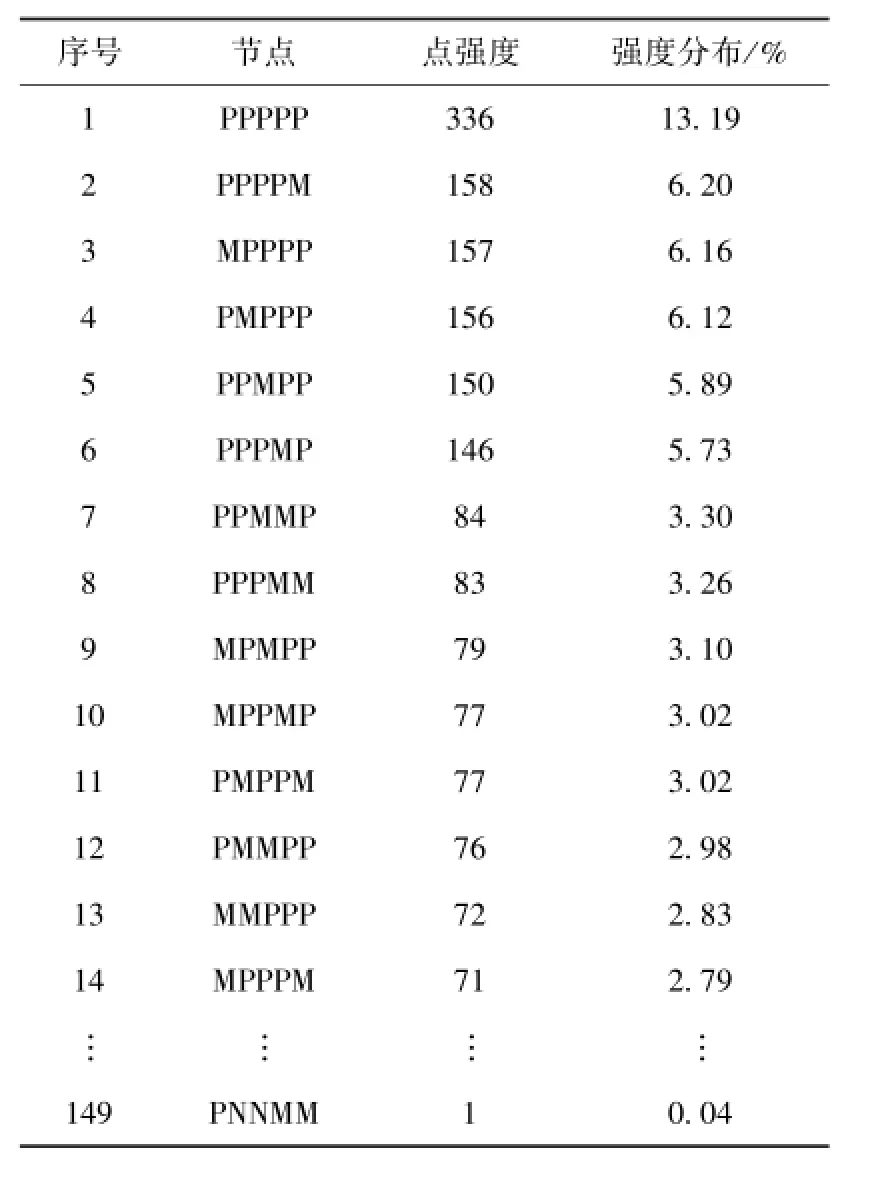
表2 聯動波動復雜網絡各節點點強度及強度分布Table 2 Strength degrees and distribution of nodes of a linkage fluctuation complex network

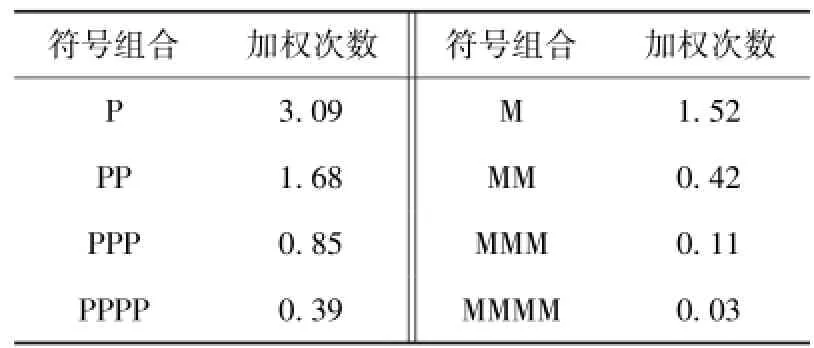
表3 前32個模態聯動性符號組合加權次數Table 3 Weighted counts of linkage fluctuation combination symbols of former 32 nodes

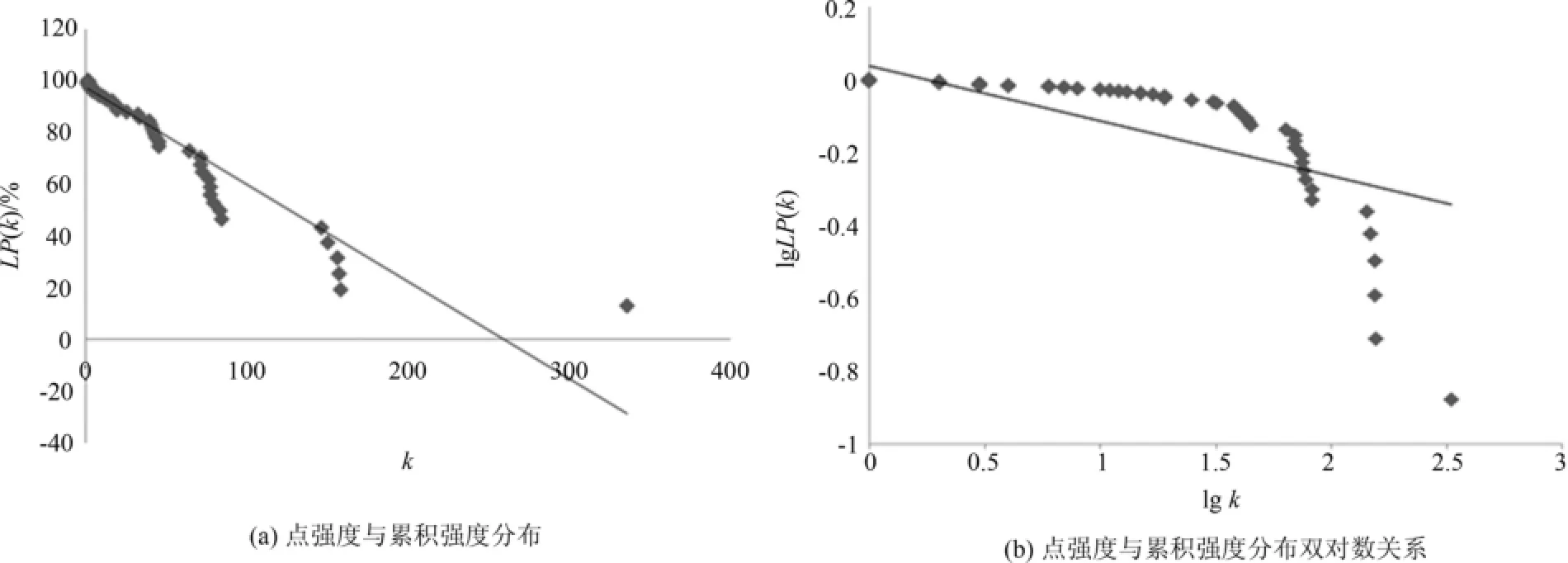
圖2 （a）點強度與累積強度分布；（b）點強度與累積強度分布雙對數關系Fig.2 （a）Distribution of strength degree and accumulation strength degree；（b）Double logarithm distribution of strength degree and accumulation strength degree

由以上分析可知，時間序列雙變量倫敦金與Au9999收盤價格聯動波動復雜網絡點強度與強度分布、排序名詞均服從冪律分布，且同向聯動性趨勢較強.說明我國黃金現貨價格Au9999受到倫敦金價格的影響，且基本保持同步.但是二者之間并非完全同步，表明我國在制定黃金現貨價格時，并不是完全與國際價格一致，而是根據我國政治經濟環境作適當調整.

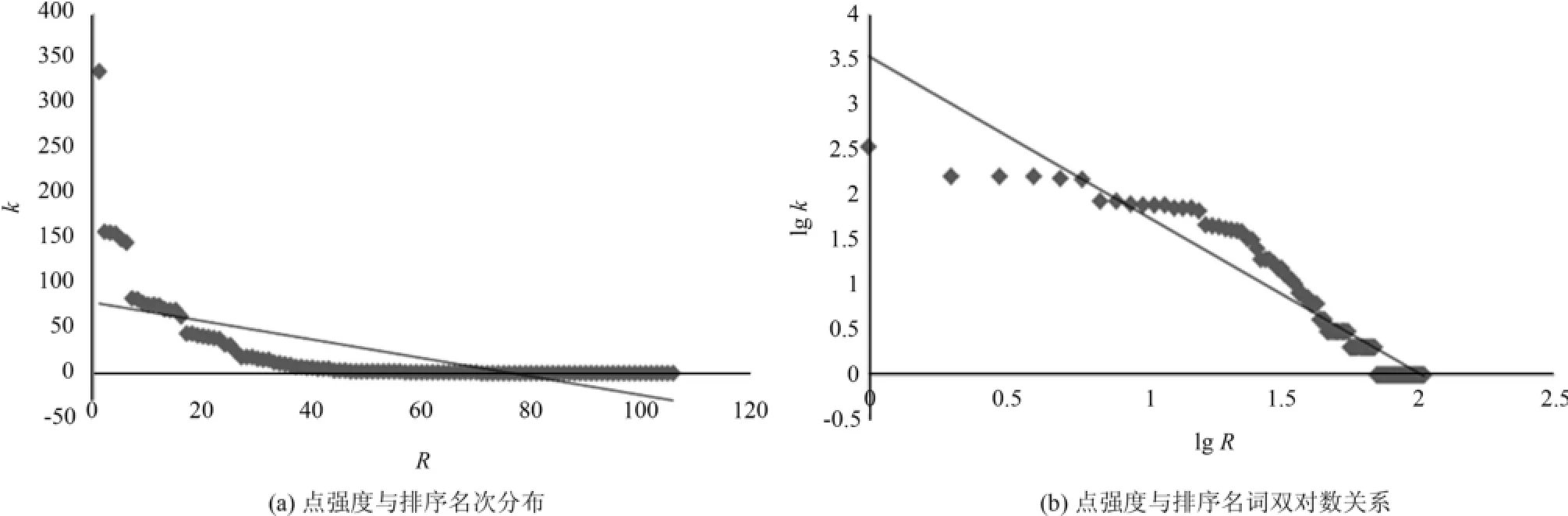
圖3 （a）點強度與排序名次分布；（b）點強度與排序名詞雙對數關系Fig.3 （a）Distribution of strength degree and its ranking；（b）Double logarithm distribution of strength degree and its ranking

2.2 聯動波動模態變化規律研究

運用n-Cliques對倫敦金與Au9999價格聯動波動復雜網絡進行統計研究，當n＝2，節點規模為7時，存在11個子群；當n＝2，節點規模為8時候，存在2個子群，結果如表4所示.

表4 n-Cliques方法聯動波動復雜網絡子群集合Table 4 Clusters of a linkage fluctuation complex network based on n-Cliques

表4中，13個子群中模態之間的相互轉換最多不超過2步，當某一模態屬于一子群時，此模態轉化為同一子群內其他模態概率較大.13個子群根據其模態可分為二類：1－11號子群中，符號P和M出現次數相當，價格正向聯動與異向聯動相互轉換頻率較高；12－13號子群中，符號M出現次數較多，在這兩個子群中，持續的異向聯動波動相互轉換概率較大.在某些子群中，價格聯動波動以同向為主，但黃金現貨市場有時會根據實際情況進行微小調整，例如小團體“NMPPP、MMPPP、MPPPP、PMPPP、PPPMM、PPPMP、PPPPM、PPPPP”中就存在9天的異向聯動.當進入小團體模態時，價格聯動變化遵循一定規律，能對黃金市場交易、風險投資及規避經濟風險提供決策參考.運用k-Plex方法，當k＝2，節點規模為4時，共存在33個子群，在這33個子群中，每個節點都至少與3個節點直接有邊相連，且向這些節點轉化較頻繁；當k＝2，節點規模為5時，不存在子群.

通過對網絡的子群進行統計分析有助于掌握聯動波動變化過程中那些模態變化較為頻繁和迅速.但是要挖掘核心模態及不同模態在轉換過程中的重要性，還需要對此網絡的聚集系數進行分析.

實驗發現整個網絡中僅有14個模態的加權集聚系數不為零，前7個節點占比86%，即這14個模態的近鄰節點之間有關聯，形成了以這些模態為核心的14個小群簇（見表5）.在復雜網絡中，若節點的聚集系數較高，度值也較高，則說明該節點在網絡中具有一定的主導地位.建立節點加權聚集系數與點強度的分布發現，兩者之間并沒有表現出良好的相關性，時間序列雙變量聯動波動復雜網絡表現出較高的復雜性，如圖4所示.

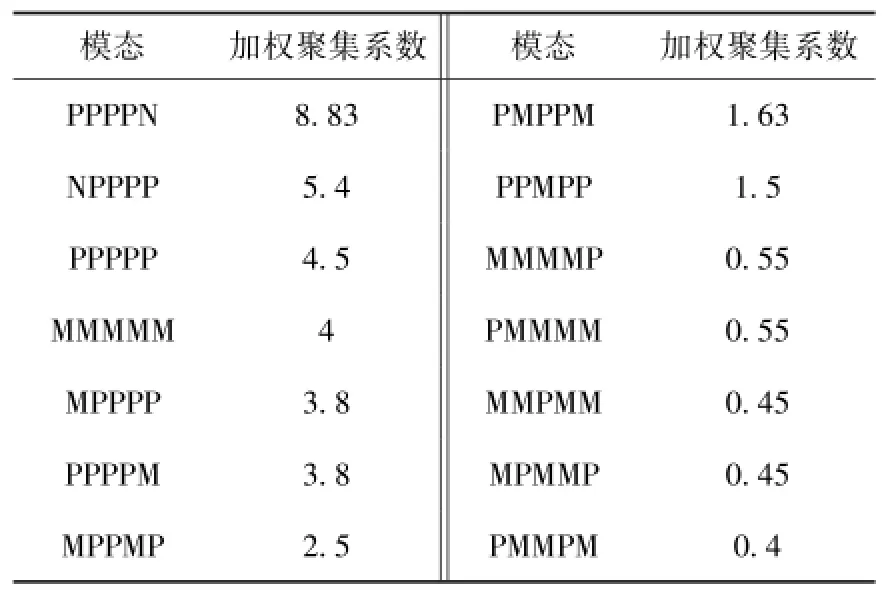
表5 各模態及其加權聚集系數Table 5 All models and their weighted clustering coefficients

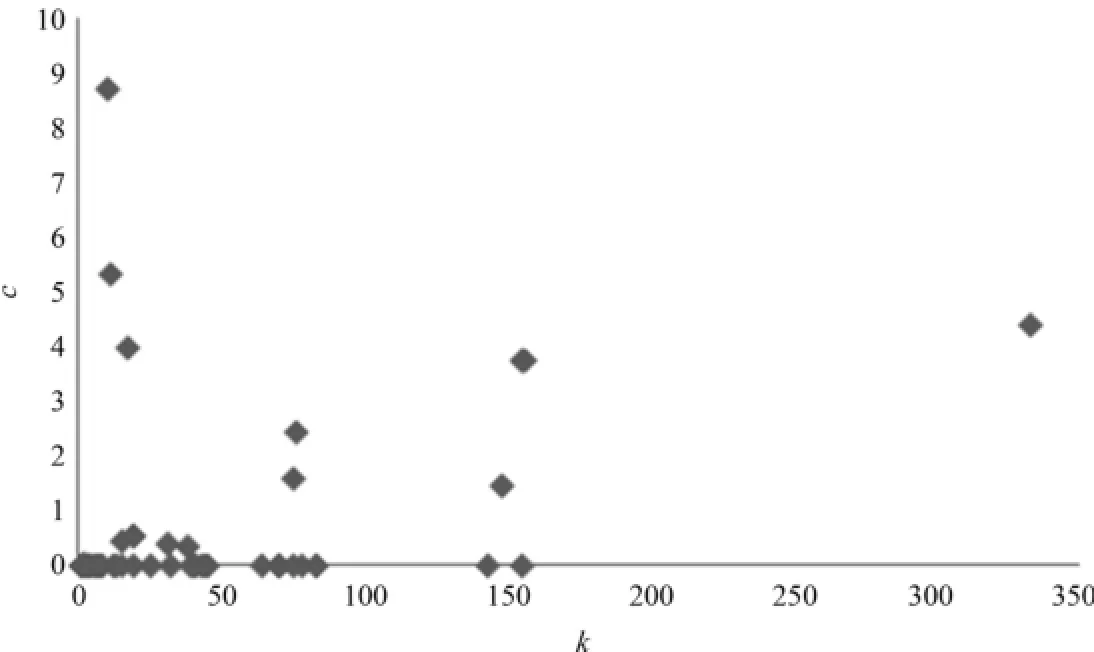
圖4 節點加權聚集系數與點強度分布Fig.4 Distribution of weighted clustering coefficients and strength degrees

2.3 聯動波動模態的演化規律

通過對此網絡的中介中心性進行計算發現模態MPPPM、PPPMP、PPPPM、PPPMM、MMPPP、PPMPN中介中心性較高，其中MPPPM為組群1、2、8、9的核心模態，PPPMP為組群1－7的核心模態.研究節點中介性與節點強度發現，某些點強度較高的節點（如PPPPP）中介中心性很弱，某些點強度較低的節點（如PPMPN或NPPPP）反而充當著網絡中重要的中介功能.當網絡中出現如PPMPN或NPPPP節點時，說明該時期為倫敦金與Au9999價格聯動波動的過渡時期，從而可以對下一時期的波動狀態做出預測.

對節點的中介中心性與等級數取雙對數，結果如圖5所示.由圖5可知，雙對數坐標系下，等級數與中心性呈冪律關系.

通過對時間序列雙變量聯動波動復雜網絡中節點中介性進行分析，發現此網絡中某些節點的中介性較高，這意味著網絡中任意兩個價格聯動波動模態之間的轉換經過這些節點中轉的可能性較大，這些節點對控制其他節點的轉換具有重要意義，它們在一定程度上可以作為聯動波動模特之間轉換的前兆，對其進行研究將有利于更好的把握黃金價格變化的規律性，為規避市場風險提供決策支持.

時間序列雙變量聯動波動復雜網絡是一個有向加權網絡，通過計算發現此網絡的平均路徑長度為7.670，網絡基于距離的聚類系數為0.166（范圍從0到1，值越小代表集聚性越弱），加權距離為0.833.結合加權聚集系數分析結果可知，在10個小族群中，模態之間轉化不需要經過多次路徑，而在這10個族群之外的其他模態節點之間平均轉換周期為7.7.

此網絡基于距離的聚類系數為0.166，接近于0，這表明此網絡聚集性很弱，盡管此網絡中存在10個小族群，但每個族群中模態數量較少，并且族群間關聯性也較弱.例如，節點PPPPP與MMMMM聚集系數相對較高，但此兩個節點之間如要進行轉換至少需要5步（PPPPP→PPPPM→PPPMM→PPMMM→PMMMM→

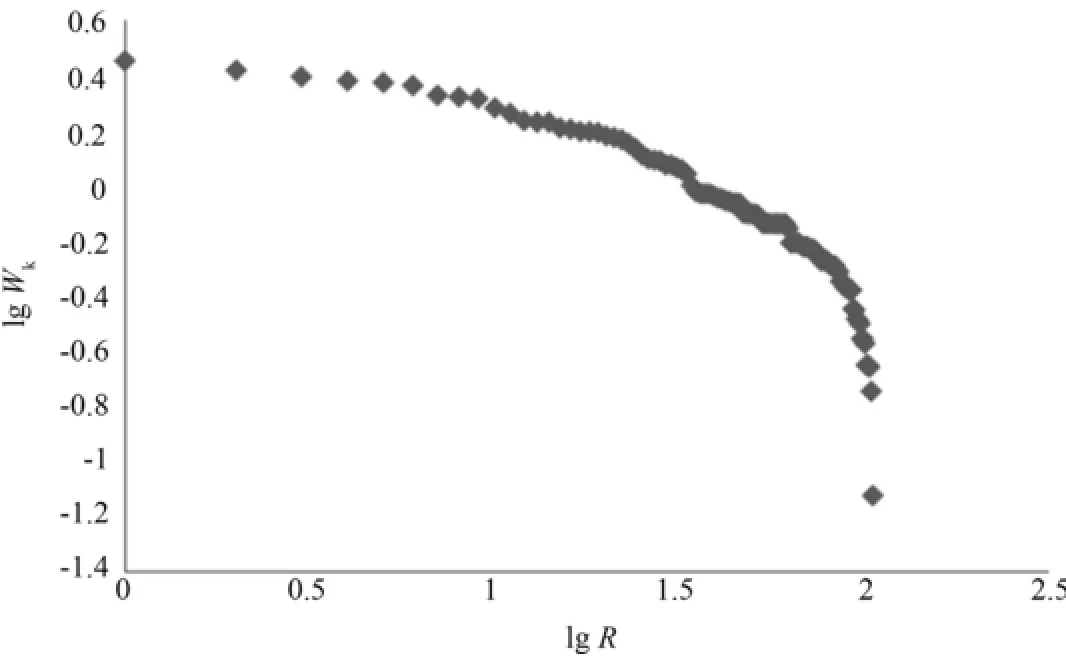
圖5 等級數與中介中心性雙對數Fig.5 Distribution of betweenness centrality and ranking

MMMMM），如圖6所示.

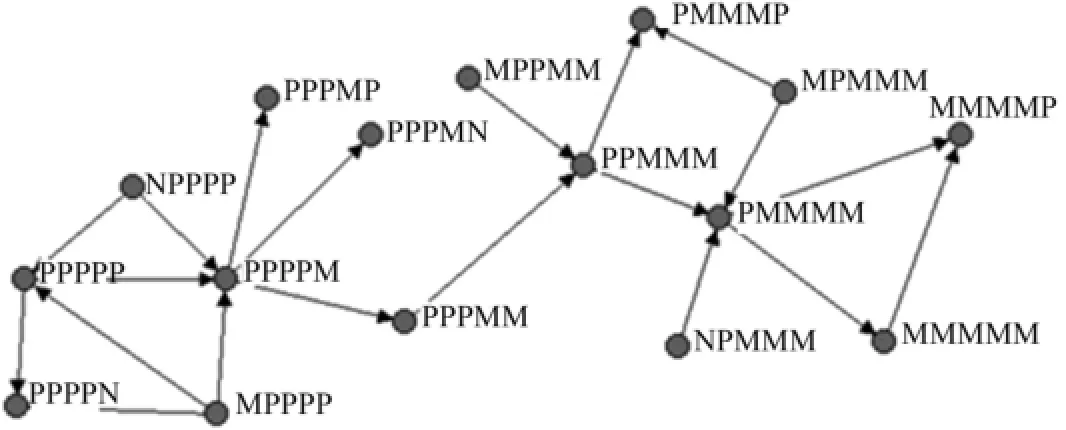
圖6 模態PPPPP與MMMMM轉換過程示意圖Fig.6 Transformation process of PPPPP and MMMMM

3 結論

時間序列雙變量聯動波動是一個非線性、非穩定的復雜系統.現有的傳統經濟學中的方法很難揭示其波動機理，而物理經濟領域的研究為我們提供了一些新的思路和方法.對于此類問題，國內外學者通常根據一定的規則將單時間序列變量波動狀態轉化為特定的符號，運用復雜網絡對其波動狀態（即變量的升與降）進行統計分析，但是對雙變量聯動波動模態變動及內在演化機理卻沒有涉及.

選擇時間序列雙變量倫敦金與Au9999價格作為樣本數據，對其聯動波動狀態進行粗粒化，步長為1天作數據滑動，構建連續五天的價格聯動波動模態.借鑒復雜網絡理論，構建時間序列雙變量聯動波動復雜網絡模型，通過對復雜網絡模型進行分析，對其模態分布規律、變化規律和演化機理進行了研究.

由于時間序列雙變量聯動波動是一個非線性的、動態變化的復雜系統，常受到國際政治經濟環境及其他因素的影響，且現實社會中存在不同的時間序列變量，其聯動波動具有不同的分布特征和演化機理.下一步將收集更多的數據，對時間序列雙變量影響因素及不同類型變量聯動波動進行研究.

［1］ 蘇木亞，郭崇慧.基于主成分分析的單變量時間序列聚類方法［J］.運籌與管理.2011，20（6）：66－72.

［2］ Armstrong J S.Long range forecasting：From crystal ball to computer［M］.2nd ed.New York：Wiley，1985.

［3］ Filders R，Lusk E J.The choice of a forecasting model［J］.Omega，1984，12：427－435.

［4］ Hill G，Filders R.The accuracy of extrapolative methods：An automatic Box-Jenkins package sift［J］.Journal of Forecasting，1984，3：319－323.

［5］ Meade N，Smith I M.ARARMA vs ARIMA-A study of the benefits of a new approach to forecasting［J］.Omega，1985，13：519534.

［6］ Pandit S M，Wu S M.Time series and system analysis with application［M］.New York：Wiley，1983.

［7］ Thury G，Anderson In O D，et al.Time series analysis：Theory and practice 1：Modeling private consumer expenditure in Austria by intervention analysis［M］.Armsterdam：North-Holland，1980：349－364.

［8］ Abraham B，Ledolter J.Statistical methods for forcasting［M］.New York：Wiley，1983.

［9］ 魏曉琴，潘妍霞，陳慧芳.上海黃金市場與倫敦黃金市場價格聯動關系研究［J］.金融理論與實踐，2012，3：46－52.

［10］ Yen H L，Hsu Ning H.Jump dynamics with structural breaks for crude oil prices［J］.Energy Econ，2012，32：343－350.

［11］ 鄭濤.金屬期貨與現貨市場價格互動關聯規則挖掘研究［J］.企業經濟，2011，（1）：166－169.

［12］ Kaufmann R K，Ullman B.Oil prices，speculation，and fundamentals：Interpreting causal relations among spot and future prices［J］.Energy Economics，2009，31（4）：550－558.

［13］ Svetlana M，Russell S Energ.Cointegration between oil spot and future prices of the same and different grades in the presence of structural change［J］.Energy Policy，2009，37：1687－1693.

［14］ 周磊，龔志強，支蓉，封國林.利用復雜網絡研究中國溫度序列的拓撲性質［J］.物理學報，2008，57（11）：7380－7389.

［15］ 陳衛東，徐華，郭琦.國際石油價格復雜網絡的動力學拓撲性質［J］.物理學報，2010，7（59）：4514－4523.

［16］ 高湘昀，安海忠，等.原油期貨與現貨價格聯運性的復雜網絡拓撲性質［J］.物理學報，2010，6（60）：0659021.

［17］ 魏曉琴，潘妍霞，陳慧芳.上海黃金市場與倫敦黃金市場價格聯動關系研究［J］.金融理論與實踐，2012，3：46－52.

［18］ 高湘昀，安海忠等.原油期貨與現貨價格聯動性的復雜網絡拓撲性質［J］.物理學報，2010，6（60）：068902.

［19］ Yook S H，Jeong H，Barabási A L，Tu Y.Small world network of athletes：Graph representation of the world professional tennis player［J］.Phys Rev Lett，2010，86：5835－5838.

［20］ Wasserman S，Faust K.1994 social network analysis：Methods and applications［M］.Cambridge：Cambridge University Press，1994：275.

［21］ Ronald S B.1992 strnctural holes：The social structure of competition［M］.Cambridge：Harvard University Press，1992：66.

［22］ Barrat A，Barthelemy M，Pastor S R，Vespignani A.The architecture of complex weighted networks［J］.Sci USA，2004，101：3747－3752.

［23］ Zhou L，Gong Z Q，Zhi R，Feng G L.Influence of time delay on global temperature correlation［J］.Acta Phys Sin，2011，20（8）：380－387.

Linkage Fluctuation in Double Variables of Time Series Based on Complex Networks

AN haigang
（Management Science and Engineering，Shijiazhuang University of Economics，Shijiazhuang 050031，China）

To study linkage fluctuation of double variables of time series，we took London Gold and Au9999.Model of linkage fluctuation is consisted of characters｛P，N，M｝，using coarse graining process.Nodes of complex network are 5-symbol strings.Linkage fluctuation complex network is composed of all models and link edges between them.It indicates that models have power-law distribution，clustering and periodicity.Transmission and evolution are finished mainly by few models.It provides an analyzing method for many kinds of double variables of time series and ideas for general law of multi-variables of time series，as well.

complex networks；coarse-grained；linkage fluctuation；time series

date： 2013－11－25；Revised date： 2014－04－02

N945.2

A

2013－11－25；

2014－04－02

國家自然科學基金（71173199）、國土資源部資源環境承載力評價重點實驗室和河北省重點學科技術經濟及管理聯合資助作者簡介：安海崗（1980－），男，博士，從事復雜系統與復雜項目管理研究，E-mail：anhaigang＠163.com

1001-246X（2014）06-0742-09