基于有限差分擴展卡爾曼濾波的鋰離子電池SOC估計

劉艷莉 戴 勝 程 澤 朱樂為

（天津大學電氣與自動化工程學院 天津 300072）

1 引言

為了應對能源危機，減緩全球氣候變暖，許多國家都開始重視節(jié)能減排和發(fā)展低碳經(jīng)濟。電動汽車因為采用電力進行驅動，可以降低二氧化碳的排放量甚至實現(xiàn)零排放，所以得到各國的重視而迅速發(fā)展。

隨著電動汽車的發(fā)展,電池管理系統(tǒng)(Battery Management System,BMS)得到了廣泛應用。為了充分發(fā)揮電池系統(tǒng)的動力性能，提高其使用的安全性、防止電池過充過放，延長電池的使用壽命，優(yōu)化駕駛和提高電動汽車的使用性能，需要 BMS對電池的荷電狀態(tài)（State of Charge,SOC）進行準確估計。電池的SOC是指電池目前所存儲的能量，作用與燃油汽車系統(tǒng)中的油量表類似。但是，由于鋰離子電池結構復雜，電池的荷電狀態(tài)受工作電流、電池內阻及其周圍的環(huán)境溫度、自放電和老化等因素的影響，使得SOC的估算困難[1]。

目前，對單體電池SOC估計的主要方法有開路電壓法和安時積分法。文獻[2]介紹的開路電壓法是利用電池的開路電壓與SOC之間的對應關系，通過測量電池的開路電壓來估計SOC。開路電壓法簡單易行，但是需要靜置較長時間才能得到穩(wěn)定的開路電壓值，只適應于電池電流非劇烈變化狀態(tài)下的SOC估計，不能滿足在線檢測要求。文獻[3]應用了目前電動汽車最常使用的安時積分法，它是通過負載電流的積分估計SOC，簡單易用，但它存在不能自動確定SOC初值和有很大的累積誤差的問題。

為了達到更高的SOC估計精度，目前國內外的研究主要集中在智能算法的應用，如神經(jīng)網(wǎng)絡法、卡爾曼濾波法等。神經(jīng)網(wǎng)絡法在建好模型的前提下，依靠大量的樣本進行數(shù)據(jù)訓練可以得到較好的精度，但是這種方法對訓練方法和訓練數(shù)據(jù)的依賴性很大，目前還沒有得到很好的應用[4]。卡爾曼濾波法根據(jù)采集到的電壓電流，由遞推算法得到SOC的最小方差估計，解決SOC初值估計不準和誤差累計的問題，但是它僅用于線性系統(tǒng)[5]。采用線性系統(tǒng)對電池進行建模得到的 SOC估計精度必定受到限制。這一問題的解決辦法之一是采用擴展卡爾曼濾波（Extended Kalman Filter,EKF）[6]來進行SOC的估計，但EKF為了求取估計誤差方差通過非線性函數(shù)的傳播，需將非線性函數(shù)用Taylor級數(shù)展開并線性化，在該過程中忽略了高階項，必定會引起誤差。

本文提出了卡爾曼濾波的另一種非線性化方法——有限差分擴展卡爾曼濾波（Finite Difference Extended Kalman Filter，F(xiàn)DEKF）法，并將此方法應用到電池SOC估計中。利用有限差分方法[7]代替EKF算法中非線性函數(shù)的偏導運算，其精度高于Taylor級數(shù)的一階展開，而且充分利用了由模型線性化產(chǎn)生的有效誤差信息，具有較強的魯棒性。本文建立了進行動力電池SOC估計的模型，給出了針對該模型利用FDEKF進行電池SOC估計的關鍵步驟和算法，并通過實驗對算法的估計精度、復雜度及魯棒性進行了驗證。

2 鋰離子電池等效模型與參數(shù)辨識

2.1 鋰離子電池模型

電池模型的種類很多，如電化學模型、等效電路模型、神經(jīng)網(wǎng)絡模型等，在文獻[8]中給出了很好的總結。電化學模型[9]基于電化學理論采用數(shù)學方法描述電池內部的反應過程，能夠全面描述電池反應的動態(tài)特性，但是電化學模型要求已知電池的化學參數(shù)、結構參數(shù)甚至材料特性等，而這些參數(shù)很難得到，因此電化學模型難以應用到電動汽車仿真與建模中，一般僅用于電池性能分析與設計中。神經(jīng)網(wǎng)絡模型[10]具有自學習能力，并且能夠模擬電池充放電過程的非線性特性，已廣泛應用于各種電池系統(tǒng)的建模仿真中。但神經(jīng)網(wǎng)絡方法受訓練數(shù)據(jù)和訓練方法的影響很大，而且經(jīng)此數(shù)據(jù)訓練的神經(jīng)網(wǎng)絡模型只能在原訓練數(shù)據(jù)的范圍內使用，因此神經(jīng)網(wǎng)絡模型更適用于批量生產(chǎn)的成熟產(chǎn)品。等效電路模型結構簡單，物理意義清晰，能夠用數(shù)學模型解析表達，便于參數(shù)辨識，在目前的研究中得到了廣泛應用。

目前被廣泛應用于電動車輛仿真的電池等效電路模型主要有 Rint模型[11]、Thevenin 模型[12]、PNGV模型[13]和多階動力學模型[14]等。前3個模型結構簡單，但難以準確反映電池的動態(tài)特性；多階模型可以達到很高的精度，但隨著階數(shù)的增高，計算量也相應增大，難以實際應用。綜合考慮模型精度、復雜度以及實驗選用的LiFePO4，本文采用圖1所示的二階RC等效電路模型。

圖1 二階RC等效電路模型Fig.1 Equivalent circuit of second-order RC model

圖中，Uoc表示開路電壓（Open Circuit Voltage，OCV），Ut為端電壓，It為端電流；R0為歐姆內阻；Re、Ce和Rd、Cd用來描述電池的極化效應。由于鋰離子電池工作的物理化學過程相當復雜，要描述清楚也相當困難，因而，可以大致地把鋰離子的運動分成在電極間的傳輸過程與在電極上的擴散過程兩個部分。

2.2 辨識方法

為了建立一個準確的電池模型，需要對模型中的未知參數(shù)進行辨識[15]。目前常用的鋰離子電池參數(shù)估計的方法有脈沖放電法[16]、最小二乘法[17]等。

脈沖放電方法適合離線估計模型參數(shù)的初始值，其基本方法是將電池靜置較長一段時間后，讓電池以恒定電流放電一段時間，并記錄下電池的電壓響應，然后根據(jù)電壓和電流計算模型的參數(shù)。其計算簡單容易實現(xiàn)，但只能用于離線的參數(shù)估計，具有一定的局限性。

最小二乘法是一種古老的數(shù)據(jù)處理方法，在辨識和參數(shù)估計領域中，最小二乘法已經(jīng)是一種基本的重要估計方法，許多用于系統(tǒng)辨識的估計算法也往往可以解釋為最小二乘法。

假設被辨識系統(tǒng)差分方程的最小二乘法形式為

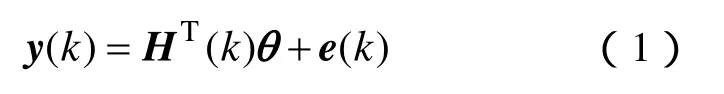
式中，y(k)為系統(tǒng)輸出量的第 k次觀測值；H為觀測向量，HT(k)=[-y(k-1)…-y(k-n) u(k)…u(k-n)]；u(k)為系統(tǒng)的第 k次輸入值；θ為被辨識的參數(shù)，θ=[α1…αnβ0β1…βn]；e(k)為均值零噪聲。

取準則函數(shù)

上面給出了最小二乘一次完成算法，但具體使用時不僅占用內存大，而且不能用于在線辨識，解決這個問題的方法是把它轉化為遞推算法。

遞推最小二乘法的基本思想是新估計值?(1)k+θ是在舊估計值?()kθ的基礎上，利用新觀測數(shù)據(jù)對老估計值?()kθ進行修正得到的。遞推最小二乘法無需存儲全部數(shù)據(jù)，取得一組觀測數(shù)據(jù)，便可估計一次參數(shù)，因此所需的計算量和占用的存儲空間都很小，而且能夠實現(xiàn)在線實時辨識。這樣，隨著觀測數(shù)據(jù)的逐次引入，一次接一次地進行參數(shù)估計，直到參數(shù)估計值達到滿意的精確度為止。

遞推最小二乘法遞推公式[18]為

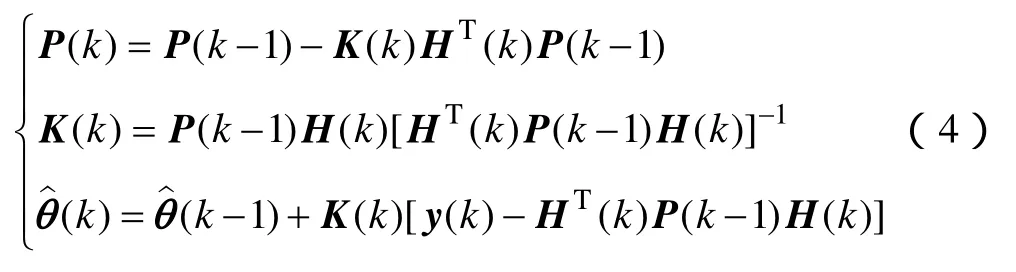
式中，K(k)為增益因子；P(k)是第k次測量的協(xié)方差陣。

2.3 參數(shù)辨識

在圖1所示電池模型中，系統(tǒng)輸入是端電流It，輸出U為開路電壓Uoc與端電壓Ut之差，由基爾霍夫定律與拉普拉斯變換導出頻域算式

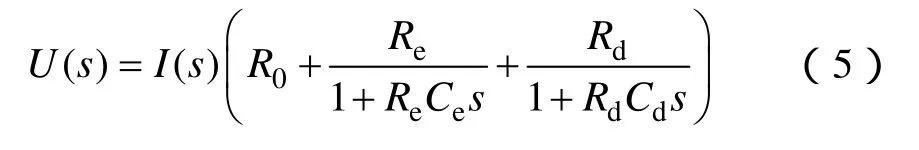
將式（5）展開后，轉化為差分方程可得

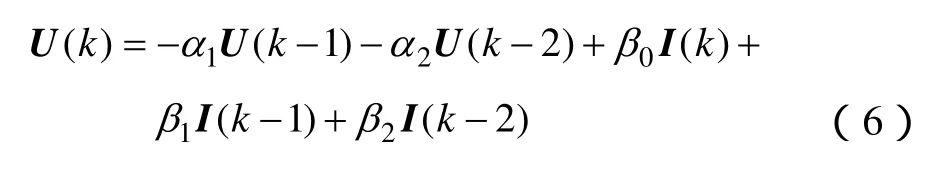
對式（6）整理，令θ=[α1α2β0β1β2]T，HT(k)=[-U(k-1)-U(k-2) I(k) I(k-1) I(k-2)]，得到最小二乘法的形式

然后利用遞推式（4）可求出 α1、α2、β0、β1和β2的值。

3 鋰離子電池的SOC估計

3.1 基于擴展卡爾曼濾波的SOC估計

圖1所示電池模型以荷電狀態(tài)SOC、兩電容上的電壓Ue、Ud為狀態(tài)變量，端電流It為輸入量，端電壓Ut為輸出量，模型離散化后的狀態(tài)方程和觀測方程分別為式（8）、式（9）

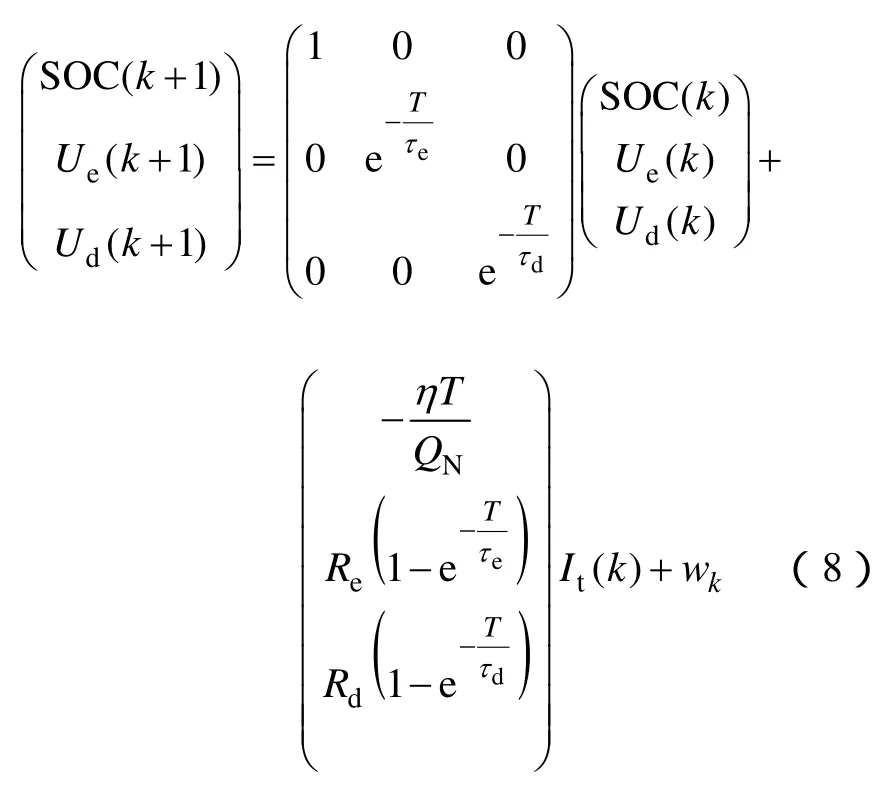
式中，η為庫侖效率[19]，可以通過電池充放電實驗得到；QN為電池額定容量；T為采樣周期；τe、τd是RC網(wǎng)絡的時間常數(shù)，且τe=ReCe，τd=RdCd；It(k)為k時刻的電流，本文中，充電時It(k)<0，放電時It(k)>0；wk和 νk是互不相關的高斯白噪聲，且假設有如下統(tǒng)計學特性

式中，Qk、Rk都為正定對稱陣；δkj為 Kronecker-δ函數(shù)。

電池開路電壓OCV與SOC存在一一對應的關系，用Uoc(SOC(k))表示該關系，該關系可以通過實驗得到（見圖2）。

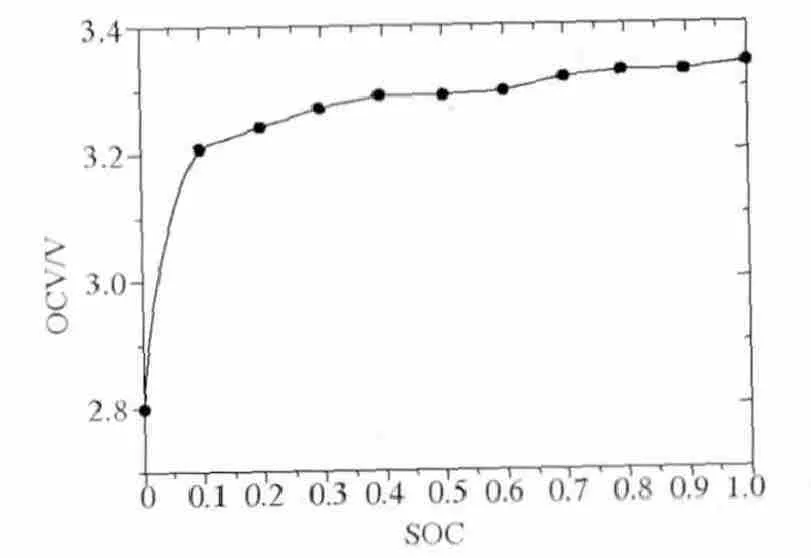
圖2 OCV-SOC關系曲線Fig.2 OCV-SOC curve

由于 OCV-SOC呈非線性關系，因此模型是非線性的，本文無法直接使用卡爾曼濾波來進行系統(tǒng)狀態(tài)的估計。一種常用方法是將它們用Taylor級數(shù)進行展開，并取其一階線性量對原函數(shù)進行線性近似后再采用卡爾曼濾波進行估計，具體步驟如下：

令xk=[SOC(k) Ue(k) Ud(k)]，上標“￣”表示驗前估計，符號“^”表示驗后估計。對狀態(tài)方程式（8）和觀測方程式（9）線性化處理，即圍繞 ?kx進行泰勒級數(shù)展開，略去二次以上項。

初始化

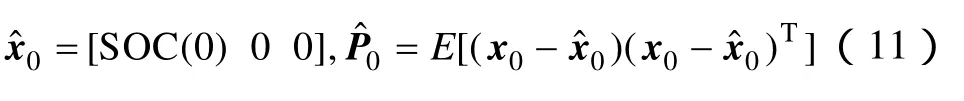
循環(huán)遞推計算

3.2 基于有限差分擴展卡爾曼濾波的SOC估計

擴展卡爾曼濾波在狀態(tài)估計過程中，存在兩個缺點：①當非線性函數(shù)的Taylor展開式高階項無法忽略時，線性化會使系統(tǒng)產(chǎn)生較大誤差，甚至使濾波器不穩(wěn)定。②在每個濾波周期需要計算 Jacobian矩陣，對于復雜系統(tǒng)，將大大增加濾波估計的運算量。有限差分擴展卡爾曼濾波則是另一種迭代型最小方均差誤差估計器，它應用有限差分代替非線性函數(shù)的偏導數(shù)計算，其精度高于Taylor級數(shù)的一階展開。

有限差分的思想最早由 Schei[20]提出，該算法的理論基礎是，采用多項式近似技術和一階中心差分法計算非線性函數(shù)的偏導數(shù)，它具有一階非線性函數(shù)近似的能力。設非線性函數(shù)y=f(x)，則其在x =處的一階有限中心差分展開為

式（17）用Taylor級數(shù)展開后為

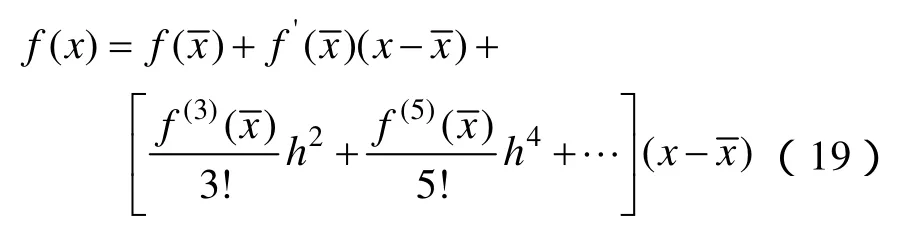
比較式（18）和式（19）可以看出，式（19）右邊的前2項與一階Taylor展開式相同，后1項對應高階項，其精度由h控制。顯然，用中心差分代替一階導數(shù)得到展開式的精度高于一般一階 Taylor級數(shù)的精度，而且適用于不同非線性函數(shù)。有限差分擴展卡爾曼濾波的實現(xiàn)如下：

對 Qk，Rk，（驗前狀態(tài)方差），（驗后狀態(tài)方差）進行Cholesky分解，有

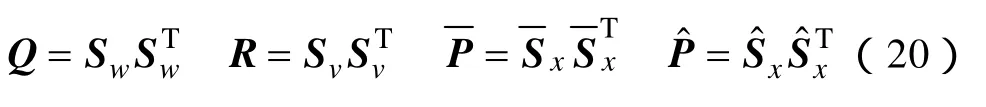
利用一階中心差分計算非線性函數(shù)偏導數(shù)，即

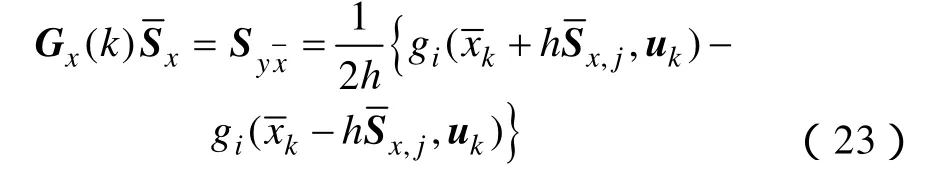
（1）驗前方差估計為

（2）驗后增益矩陣和方差估計為

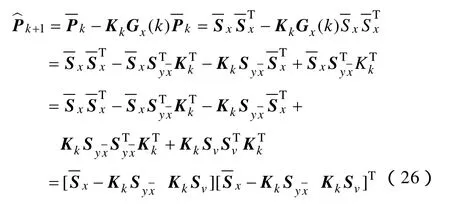
那么，式（24）～式（26）替換EKF算法流程中的式（13）、式（14）、式（16），即組成 FDEKF算法。

從上述推導過程來看，驗前方差、驗后方差和驗后增益矩陣的計算，綜合考慮了過程噪聲的影響和模型線性化誤差的影響 。因此，應用有限差分對EKF的改進，可以增加算法的精確性和魯棒性。

4 實驗分析

本文測試選用的電池是天津力神公司生產(chǎn)的磷酸鐵鋰動力電池LP2770102AC，電池的標稱電壓為3.3V，標稱容量為12.5A·h。測試是在Digatron動力電池測試系統(tǒng)上進行，為驗證算法的性能，設計了脈沖放電，用來估算模型參數(shù)和驗證SOC算法的精度。

4.1 模型驗證

實驗具體實現(xiàn)如下：將電池組充滿電(SOC(0)=100%)，在恒溫條件下(20℃±2℃)對電池組進行脈沖放電（4.17A放電18min，靜置60min），整個放電過程時長 780min，采樣間隔為 1s。圖3為實驗過程中采集的端電流和端電壓。

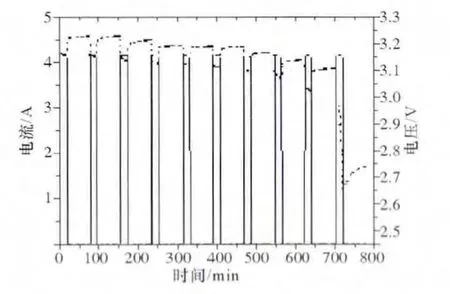
圖3 脈沖放電端電流/電壓波形Fig.3 Terminal current/voltage curves by pulse discharge

為了研究遞推最小二乘法的辨識結果，本文對圖3所示的脈沖放電工況進行辨識，參數(shù)辨識結果如圖4所示。為真實反映電池動態(tài)特性，在Matlab/Simscape中搭建如圖5所示的等效電路模型，將電流加載到模型上得到仿真電壓。圖6是根據(jù)估計的仿真電壓和實測電壓比較曲線，從圖6中可以看出，在 692min以前，等效電路模型可以準確反映鋰離子電池實際的動態(tài)特性，誤差在20mV以內。在最后一個放電區(qū)間（SOC＜0.1），電池實際電壓劇烈跌落，從參數(shù)辨識曲線可以看出，極化電容Ce、Cd均劇烈變化，模型仿真電壓與實測電壓也存在較大誤差(200mV)。

圖4 參數(shù)辨識曲線Fig.4 Parameters identification curve

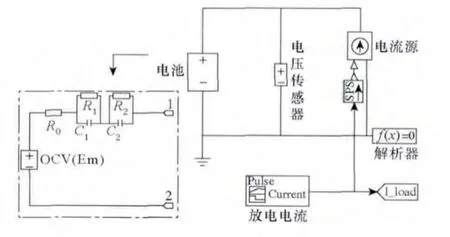
圖5 Simscape等效電路模型Fig.5 Equivalent circuit of simscape model

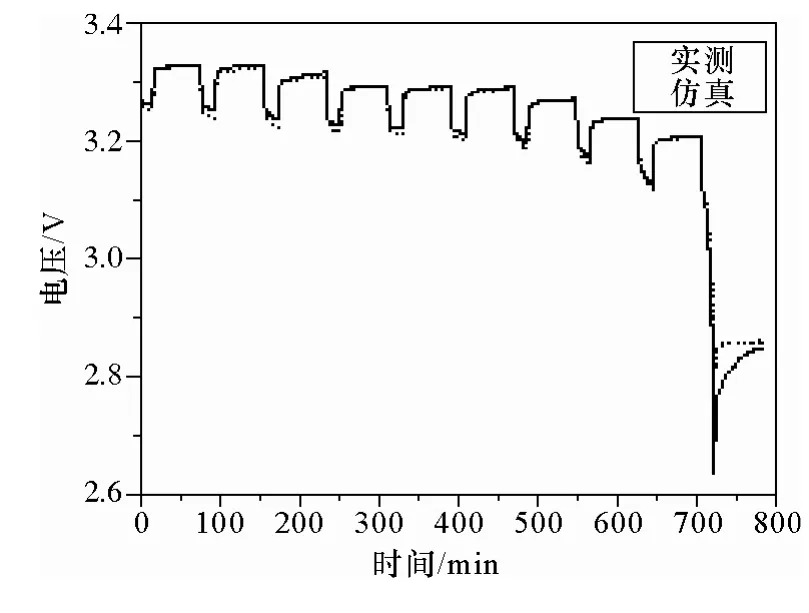
圖6 端電壓曲線Fig.6 Terminal voltage curve

4.2 算法驗證

分別采用擴展卡爾曼濾波和有限差分擴展卡爾曼濾波估計電池SOC，實驗結果如圖7所示。

圖7 脈沖放電下的SOC估計及誤差曲線Fig.7 Comparison of SOC estimation and error curve by pulse discharge with same current

為了定量的比較EKF和FDEKF的性能，分別定義方均根誤差和算法的平均耗時為

式中，T表示一次實驗的時間步長；?kx表示狀態(tài)SOC的第k步的估計值；xk表示狀態(tài)SOC的第k步的真實值；為第k步實驗算法耗時時間。

表 SOC估計比較Tab.Comparison of SOC estimation

通過圖7可以看出，在模型較為準確時(0.1＜SOC＜1)，此時EKF算法和 FDEKF算法均能較好的估算電池SOC，其中EKF算法的最大誤差為6%，而FDEKF算法的最大誤差為2%，說明FDEKF算法精度高于EKF算法。而在電池SOC＜0.1時,電池等效模型存在一定偏差，此時 FDEKF算法仍能準確跟蹤實際值，但 EKF算法在模型失效時的 SOC估計值存在較大偏差，說明 FDEKF具有較好的魯棒性。表1全面比較了EKF算法和FDEKF算法的性能，F(xiàn)DEKF算法無論是平均耗時還是均方根誤差上，均優(yōu)于EKF算法。

5 結論

本文采用了等效電路模型對鋰離子電池進行建模分析，并使用了遞推最小二乘法辨識模型參數(shù)；研究了基于有限差分擴展卡爾曼濾波的電池 SOC估計方法。實驗分析表明，采用 FDEKF算法，有利于提高動力電池SOC估計精度，且在模型存在誤差時有較好的魯棒性。

[1] 張劍波,盧蘭光,李哲.車用動力電池系統(tǒng)的關鍵技術與學科前沿[J].汽車安全與節(jié)能學報,2012(2):87-104.Zhang Jianbo,Lu Languang,Li Zhe.Key technologies and fundamental academic issues for traction battery systems[J].Journal of Automotive Safety and Energy,2012(2): 87-104.

[2] 林成濤,王軍平,陳全世.電動汽車 SOC估計方法原理與應用[J].電池,2004(5): 376-378.Lin Chengtao,Wang Junping,Chen Quanshi.Methods for state of charge estimation of EV batteries and their application[J].Battery,2004(5): 376-378.

[3] 齊國光,李建民,郟航,等.電動汽車電量計量技術的研究[J].清華大學學報(自然科學版),1997(3):47-50.Qi Guoguang,Li Jianming,Jia Hanget al.Research on the power measurement technology for electric vehicle[J].Journal of Tsinghua University(Science &Technology),1997(3): 47-50.

[4] 尹安東,張萬興,趙韓,等.基于神經(jīng)網(wǎng)絡的磷酸鐵鋰電池 SOC預測研究[J].電子測量與儀器學報,2011(5): 433-437.Yin Andong,Zhang Wanxing,Zhao Han,et al.Research on estimation for SOC of LiFePO4 Li-ion battery based on neural network[J].Journal of Electronic Measurement and Instrument,2011(5):433-437.

[5] Piller Sabine,Perrin Marion,Jossen Andreas.Methods for state of charge determination and their applications[J].Journal of Power Sources,2001,96(1): 113-120.

[6] 夏超英,張術,孫宏濤.基于推廣卡爾曼濾波算法的SOC估算策略[J].電源技術,2007(5): 414-417.Xia Chaoying,ZhangShu,Sun Hongtao.A strategy of estimating state of charge based on extended Kalman filter[J].Power Technology,2007(5): 414-417.

[7] Rulkov Nikolai F,Sushchik Mikhail M,Tsimring Lev S,et al.Generalized synchronization of chaos in directionally coupled chaotic systems[J].Physical Review E,1995,51(2): 980-994.

[8] 陳全世,林成濤.電動汽車用電池性能模型研究綜述[J].汽車技術,2005(3): 1-5.Chen Quanshi,Lin Chengtao.Summarization of studies on performance models of battery for electric vehicle[J].Automotive Technology,2005(3): 1-5.

[9] Di Domenico,Domenico,Giovanni Fiengo.Lithiumion battery state of charge estimation with a Kalman filter based on a electrochemical model[C].IEEE International Conference on Control Applications(CCA),2008: 702-707.

[10] Fang Kaizheng,Mu Daobin,Chen Shi,et al.A prediction model based on artificial neural network for surface temperature simulation of nickel–metal hydride battery during charging[J].Journal of Power Sources,2012,208(0): 378-382.

[11] Johnson V H.Battery performance models in advisor[J].Journal of Power Sources,2002,110(2):321-329.

[12] He Hongwen,Xiong Rui,Zhang Xiaowei,et al.State-of-charge estimation of the lithium-ion battery using an adaptive extended kalman filter based on an improved thevenin model[J].IEEE Transactions on Vehicular Technology,2011,60(4): 1461-1469.

[13] Gao Wengen,Jiang Ming,Hou Youming.Research on PNGV model parameter identification of LiFePO4 li-ion battery based on fmrls[Z].2011: 2294-2297.

[14] Kroeze,Ryan Carter,Krein Philip T.Electrical battery model for use in dynamic electric vehicle simulations[C].IEEE Power Electronics Specialists Conference,2008: 1336-1342.

[15] Bambach M,Heinkenschloss M,HERTY M.A method for model identification and parameter estimation[J].Inverse Problems,2013,29(2): 25009.

[16] 田甜,李孝尊,李紅梅.磷酸鐵鋰電池的改進建模及 SOC估計[J].合肥工業(yè)大學學報(自然科學版),2012(9): 1192-1195.Tian Tian,Li Xiaozun,Li Hongmei.Modified modeling and SOC estimation of LiFePO4 Li-ion battery[J].Journal of Hefei University Of Technology(Natural Science).2012(9): 1192-1195.

[17] Zhong Muda,Jiang Jiuchun.Wavelet-based identification method of li-ion battery model for electric vehicles[Z].2013: 1529-1532.

[18] Hu Yuanbiao.Iterative and recursive least squares estimation algorithms for moving average systems[J].Simulation Modeling Practice and Theory,2013,34(0): 12-19.

[19] 黃文華,韓曉東,陳全世.電動汽車 SOC估計算法與電池管理系統(tǒng)的研究[J].汽車工程,2007(3):198-202.Huang Wenhua,Han Xiadong,Chen Quanshi.A study on soc estimation algorithm and battery management system for electric vehicle[J].Automotive Engineering,2007(3): 198-202.

[20] Tor Steinar Schei.A finite-difference method for linearization in nonlinear estimation algorithms[J].Automatica,1997,33(11): 2053-2058.