主跨支撐特性對(duì)三支撐結(jié)構(gòu)振動(dòng)的影響

蘇引平，曾慶猛，傅行軍

（1.中機(jī)國能電力工程有限公司，上海200061；2.東南大學(xué) 火電機(jī)組振動(dòng)國家工程研究中心，南京210096）

發(fā)電機(jī)和勵(lì)磁機(jī)的三支撐結(jié)構(gòu)在機(jī)組中應(yīng)用較多，也較容易出現(xiàn)故障［1-2］.主跨支撐特性對(duì)軸系響應(yīng)的影響不可忽略，現(xiàn)場(chǎng)動(dòng)平衡需要考慮該因素［3］，在早期軸系動(dòng)特性研究中就考慮了滑動(dòng)軸承和軸承座［4］的影響.本文的理論模擬基于有限元法，它是一種數(shù)值計(jì)算方法，可以從所考察的物理模型出發(fā)，對(duì)物體直接進(jìn)行離散化處理，計(jì)算結(jié)果精度較高且數(shù)值穩(wěn)定.筆者采用Ansys有限元軟件，基于某機(jī)組建立了軸系的有限元模型，然后利用Ansys中的模態(tài)分析模塊和諧響應(yīng)分析模塊研究三支撐結(jié)構(gòu)的振動(dòng)特性并進(jìn)行試驗(yàn)驗(yàn)證.

1 三支撐結(jié)構(gòu)振動(dòng)特性的理論模擬

1.1 有限元建模及模態(tài)分析

根據(jù)某1 000 MW 機(jī)組建立軸系有限元模型，軸系由高壓缸、4個(gè)低壓缸、發(fā)電機(jī)和勵(lì)磁機(jī)轉(zhuǎn)子組成，為減小計(jì)算工作量，只分析低壓缸、發(fā)電機(jī)和勵(lì)磁機(jī)連成的軸系，且這與對(duì)整個(gè)軸系的計(jì)算結(jié)果相比誤差很小.軸系有限元模型見圖1.

若支撐系統(tǒng)的基礎(chǔ)及軸承座剛性較好，則基礎(chǔ)及軸承座可簡(jiǎn)化為質(zhì)量-彈簧-阻尼器模型，軸承座及基礎(chǔ)在x、y方向的參振質(zhì)量 分別用Mb，x和Mb，y表示，x、y方向耦合較弱，不考慮交叉剛度和交叉阻尼的影響，支撐系統(tǒng)可簡(jiǎn)化為圖2（a）所示的模型.在圖2中，kb，x、kb，y分別為軸承座及基礎(chǔ)在x、y方向 的等效靜 剛 度 系 數(shù)；kp，x、kp，y分 別 為 油 膜 在x、y方向的剛度系數(shù)；cx、cy分別為支撐系統(tǒng)在x、y方向的等效阻尼系數(shù).

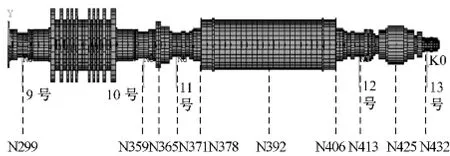
圖1 軸系有限元模型Fig.1 Finite element model of the shafting

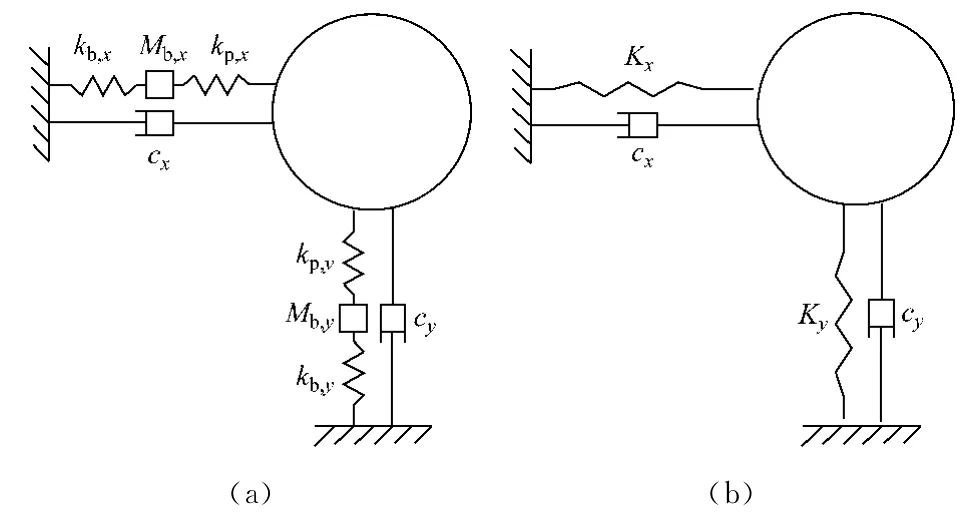
圖2 支撐系統(tǒng)的簡(jiǎn)化示意圖Fig.2 Simplified diagram of the supporting system

圖2（a）的支撐模型還可以進(jìn)一步簡(jiǎn)化為更簡(jiǎn)單的彈性支撐模型，如圖2（b）所示.參振質(zhì)量在y方向的運(yùn)動(dòng)微分方程為

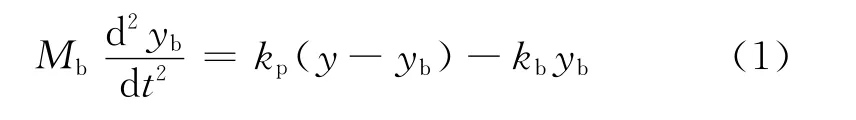
由此方程求得軸承座中心坐標(biāo)yb與軸頸中心坐標(biāo)y之間的關(guān)系

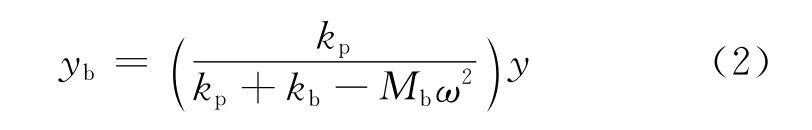
代入圖2（a）與圖2（b）的等效關(guān)系式

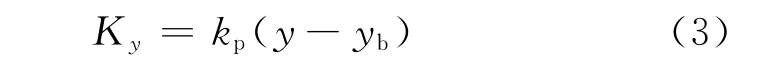
得圖2（b）等效支撐的相應(yīng)剛度系數(shù)K為

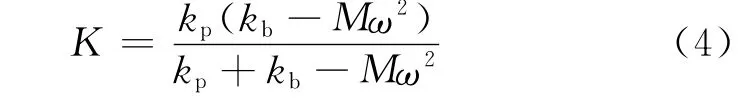
式中：K為滑動(dòng)軸承的支撐總剛度系數(shù)，這一系數(shù)綜合反映了油膜、軸承座及基礎(chǔ)的動(dòng)力特性.與一般的等剛度的支撐不同，此支撐的總剛度系數(shù)不是常數(shù)，而與轉(zhuǎn)子的渦動(dòng)角速度有關(guān)，但在軸承形式、結(jié)構(gòu)尺寸和載荷一定的條件下，在臨界轉(zhuǎn)速計(jì)算中，可用所感興趣的轉(zhuǎn)速范圍內(nèi)的平均值來代替，即視為常數(shù)，一般由此引起的誤差也較小.根據(jù)該機(jī)組軸承形式、結(jié)構(gòu)尺寸和載荷等，取發(fā)電機(jī)兩端水平、垂直支撐剛度分別為0.8×109N／m、1.3×109N／m，水平、垂直支撐阻尼分別為0.23×107（N·s）／m、1×107（N·s）／m，忽略對(duì)軸系動(dòng)力特性影響很小的交叉剛度和交叉阻尼.模態(tài)分析得到該軸系發(fā)電機(jī)一階臨界轉(zhuǎn)速為830r／min，二階臨界轉(zhuǎn)速為2 160r／min，與實(shí)測(cè)值一階臨界轉(zhuǎn)速785r／min、二階臨界轉(zhuǎn)速2 060r／min相比，誤差分別為5.7%和4.9%，模型較合理.

1.2 支撐相近情況下的不平衡響應(yīng)計(jì)算

在發(fā)電機(jī)兩端支撐特性相近的情況下，當(dāng)發(fā)電機(jī)兩端的風(fēng)扇環(huán)處存在二階不平衡和勵(lì)磁機(jī)中部N425節(jié)點(diǎn)處存在不平衡時(shí)，利用所建模型分別對(duì)其進(jìn)行諧響應(yīng)分析，得到發(fā)電機(jī)兩端11號(hào)、12號(hào)瓦處的振動(dòng)數(shù)據(jù)，然后按照諧分量法對(duì)11號(hào)、12號(hào)瓦處振動(dòng)進(jìn)行對(duì)稱和反對(duì)稱分解，得到發(fā)電機(jī)兩端的同相和反相振動(dòng)分量隨轉(zhuǎn)速的變化曲線（見圖3）.

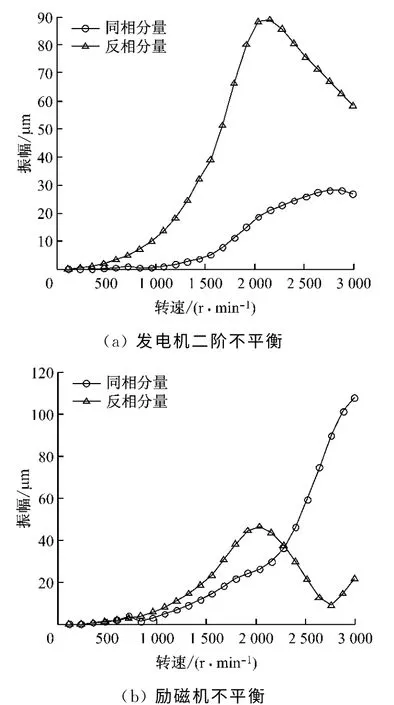
圖3 在主跨支撐特性相近情況下不平衡激起的同相和反相振動(dòng)波德曲線Fig.3 In-phase and anti-phase vibration Bode curves stimulated by imbalance with similar main-span supporting characteristics

由圖3可知：（1）發(fā)電機(jī)二階不平衡激起發(fā)電機(jī)兩端的反相振動(dòng)明顯大于同相振動(dòng)，同相振動(dòng)的幅值小于28μm，而反相振動(dòng)的幅值最大達(dá)到90μm；（2）勵(lì)磁機(jī)不平衡時(shí)，只在發(fā)電機(jī)二階臨界轉(zhuǎn)速下反相振動(dòng)較大，而在工作轉(zhuǎn)速下以同相振動(dòng)為主.

1.3 支撐差別情況下的不平衡響應(yīng)計(jì)算

1.3.1 發(fā)電機(jī)前瓦（11號(hào)）剛度較低時(shí)

將11號(hào)瓦支撐剛度降為原來的1／10，分別計(jì)算當(dāng)發(fā)電機(jī)兩端存在二階不平衡和勵(lì)磁機(jī)中部存在不平衡時(shí)軸系的響應(yīng)，然后對(duì)發(fā)電機(jī)兩端的振動(dòng)進(jìn)行諧分量分解，得到發(fā)電機(jī)兩端的同相和反相振動(dòng)隨轉(zhuǎn)速的變化曲線（見圖4）.

由圖4可知：（1）不論是發(fā)電機(jī)二階不平衡還是勵(lì)磁機(jī)不平衡，對(duì)11號(hào)瓦影響都較大，振幅與不平衡激勵(lì)成正比，而與支撐剛度成反比.（2）發(fā)電機(jī)二階不平衡激起11號(hào)瓦在二階臨界轉(zhuǎn)速下振動(dòng)很大，發(fā)電機(jī)兩端振幅差別較大，即在發(fā)電機(jī)二階臨界轉(zhuǎn)速下，不僅激發(fā)反相振動(dòng)，同相振動(dòng)也較大，如圖4（a）所示.（3）當(dāng)發(fā)電機(jī)11號(hào)瓦剛度大幅降低后，勵(lì)磁機(jī)中部不平衡激起的發(fā)電機(jī)兩端同相和反相振動(dòng)的變化趨勢(shì)及幅值基本一致，如圖4（b）所示.

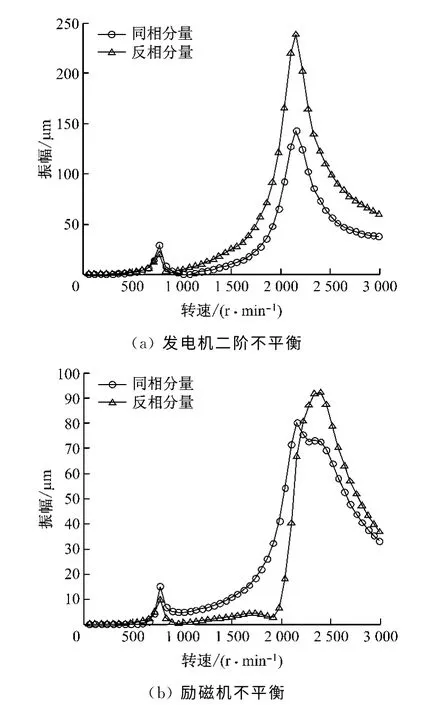
圖4 11號(hào)瓦支撐剛度降低時(shí)不平衡激起的同相和反相振動(dòng)波德曲線Fig.4 In-phase and anti-phase vibration Bode curves stimulated by imbalance with stiffness reduction of No.11pad

1.3.2 發(fā)電機(jī)后瓦（12號(hào)）剛度較低時(shí)

11號(hào)瓦的支撐剛度正常，將12 號(hào)瓦支撐剛度降為原來的1／10，加重位置和大小與第1.3.1節(jié)中相同，計(jì)算發(fā)電機(jī)兩端的振動(dòng)并進(jìn)行諧分量分解，得到發(fā)電機(jī)兩端同相和反相振動(dòng)的波德曲線（見圖5）.

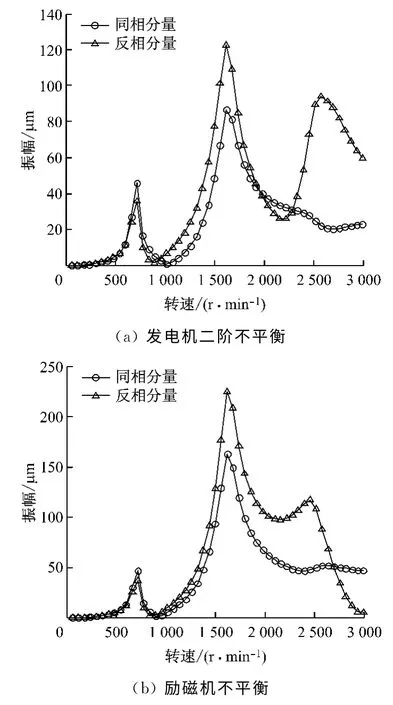
圖5 12號(hào)瓦支撐剛度降低時(shí)不平衡激起的同相和反相振動(dòng)波德曲線Fig.5 In-phase and anti-phase vibration Bode curves stimulated by imbalance with stiffness reduction of No.12pad

由圖5可知：（1）發(fā)電機(jī)二階不平衡下，12號(hào)瓦支撐剛度降低時(shí)二階臨界轉(zhuǎn)速下同相和反相振動(dòng)振幅比11號(hào)瓦支撐剛度降低時(shí)小70～110μm，這是因?yàn)殡m然12號(hào)瓦支撐剛度低，但距離12號(hào)瓦較近的13號(hào)瓦可對(duì)發(fā)電機(jī)起到一定的支撐作用，減小12號(hào)瓦剛度降低對(duì)振動(dòng)的影響，但此時(shí)發(fā)電機(jī)和勵(lì)磁機(jī)振型相互影響較大，這也是勵(lì)磁機(jī)一階臨界轉(zhuǎn)速下發(fā)電機(jī)兩端反相振動(dòng)也出現(xiàn)峰值的原因，如圖5（a）所示；（2）勵(lì)磁機(jī)存在不平衡時(shí)，發(fā)電機(jī)二階臨界轉(zhuǎn)速下，圖5（b）所示振幅比圖4（b）所示振幅大90～150μm，這是因?yàn)?2號(hào)瓦支撐作用較弱，導(dǎo)致三支撐結(jié)構(gòu)對(duì)勵(lì)磁機(jī)不平衡響應(yīng)較敏感.（3）不論是發(fā)電機(jī)二階不平衡還是勵(lì)磁機(jī)不平衡，在發(fā)電機(jī)二階和勵(lì)磁機(jī)一階臨界轉(zhuǎn)速下均存在波峰，這是因?yàn)?2號(hào)瓦支撐剛度大幅度降低后，距離12 號(hào)瓦較近的13號(hào)瓦作為三支撐結(jié)構(gòu)的末端支撐，不僅要支撐勵(lì)磁機(jī)，還要承受發(fā)電機(jī)的部分質(zhì)量，三支撐結(jié)構(gòu)的11號(hào)和13號(hào)瓦承受較大載荷，導(dǎo)致發(fā)電機(jī)和勵(lì)磁機(jī)振型相互影響.

2 三支撐結(jié)構(gòu)振動(dòng)特性的試驗(yàn)?zāi)M

為進(jìn)一步研究三支撐結(jié)構(gòu)的振動(dòng)特性，利用ZT-1轉(zhuǎn)子振動(dòng)模擬試驗(yàn)臺(tái)（見圖6）進(jìn)行試驗(yàn).試驗(yàn)臺(tái)由直流電動(dòng)機(jī)驅(qū)動(dòng)，手動(dòng)調(diào)整調(diào)速器輸出電壓可實(shí)現(xiàn)電機(jī)0～10 000r／min轉(zhuǎn)速范圍內(nèi)的無級(jí)調(diào)速.由于該試驗(yàn)臺(tái)的軸承支撐不是實(shí)際汽輪發(fā)電機(jī)組中真正意義上的油膜，可能造成通過單純地松動(dòng)支撐與底座間的連接螺絲來達(dá)到降低軸承支撐剛度的效果不明顯，所以為了盡量模擬實(shí)際支撐特性，試驗(yàn)中分別在1號(hào)、2號(hào)和3號(hào)軸承與底座之間加一薄片，這樣可通過緊固螺絲來模擬支撐特性相近的情況，而通過拆掉2號(hào)軸承下的墊片且松動(dòng)2號(hào)軸承的螺絲來模擬支撐特性差別顯著的情況.在圓盤上加不同形式的重量（配重為試驗(yàn)臺(tái)專用螺絲釘），分別模擬在各支撐螺絲擰緊和2號(hào)軸承支撐螺絲松動(dòng)情況下的響應(yīng)，1號(hào)、2號(hào)軸承處軸振對(duì)稱、反對(duì)稱分解后的同相和反相振動(dòng)分量隨轉(zhuǎn)速的變化曲線見圖7和圖8.

圖6 ZT-1轉(zhuǎn)子振動(dòng)模擬試驗(yàn)臺(tái)Fig.6 Experimental setup for vibration simulation of ZT-1rotor

在圓盤1、圓盤2上加反對(duì)稱重量，支撐螺絲均擰緊后，同相和反相振動(dòng)波德曲線如圖7（a）所示，在4 500r／min之前同相振動(dòng)大于反相振動(dòng)，之后的轉(zhuǎn)速范圍內(nèi)，反相振動(dòng)均大于同相振動(dòng).當(dāng)松動(dòng)2號(hào)軸承支撐螺絲后，同相和反相振動(dòng)波德曲線如圖8（a）所示，在高于5 500r／min的轉(zhuǎn)速范圍內(nèi)，同相振動(dòng)大于反相振動(dòng)，可見在支撐差別顯著時(shí)，主跨二階不平衡激起反相振動(dòng)的同時(shí)，也將激起較大的同相振動(dòng).

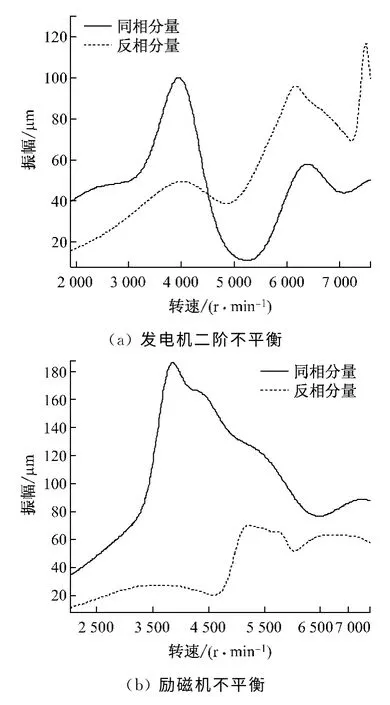
圖7 支撐螺絲擰緊時(shí)各不平衡下同相和反相振動(dòng)波德曲線Fig.7 In-phase and anti-phase vibration Bode curves stimulated by imbalance with supporting screws tightened

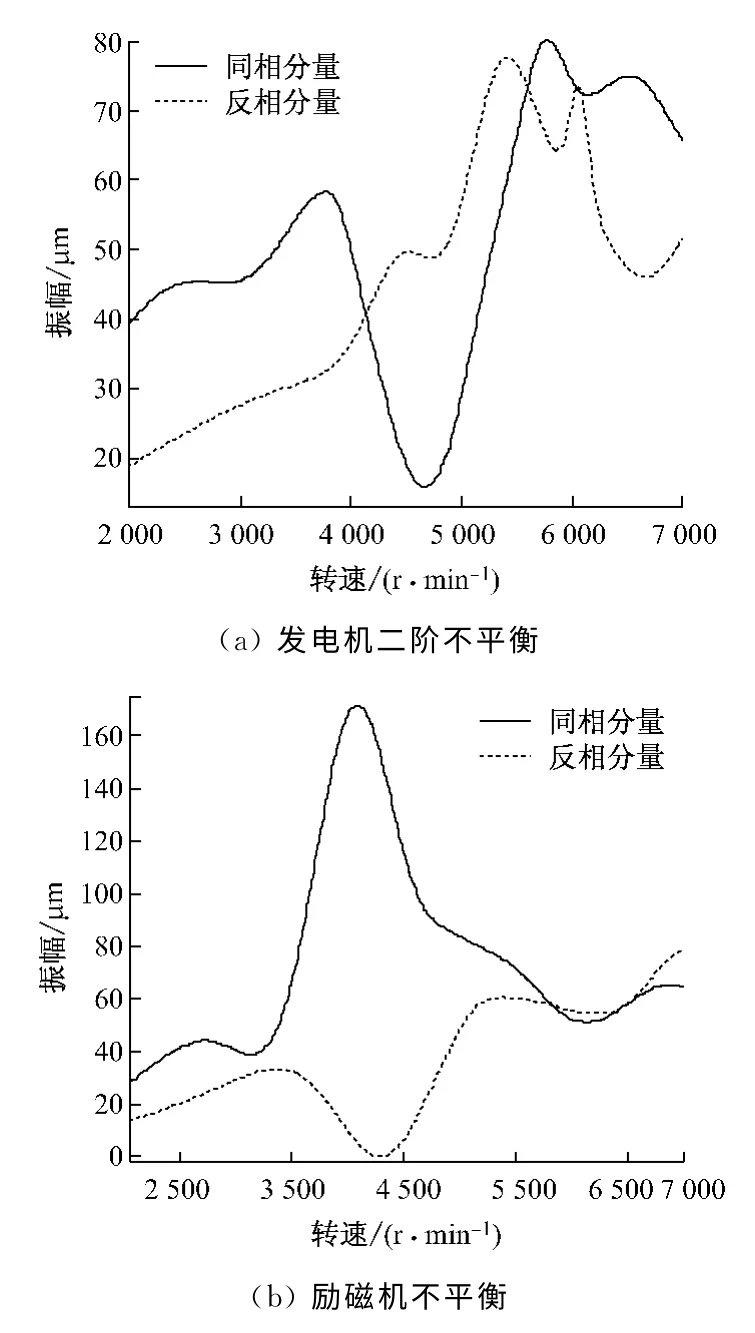
圖8 支撐螺絲松動(dòng)時(shí)各不平衡下同相和反相振動(dòng)波德曲線Fig.8 In-phase and anti-phase vibration Bode curves stimulated by imbalance with supporting screws slackened

拆掉圓盤1和圓盤2上的反對(duì)稱配重，在圓盤3上加螺絲釘.由圖7（b）可知，支撐螺絲擰緊后，勵(lì)磁機(jī)不平衡激起主跨兩端的振動(dòng)主要以同相振動(dòng)為主，在較高轉(zhuǎn)速范圍內(nèi)，同相振動(dòng)略大于反相振動(dòng).由圖8（b）可知，2號(hào)軸承支撐螺絲松動(dòng)后，勵(lì)磁機(jī)不平衡在一階臨界轉(zhuǎn)速下激起非常大的同相振動(dòng)，隨著轉(zhuǎn)速的繼續(xù)升高，反相振動(dòng)越來越大，5 500r／min以后反相和同相振動(dòng)相當(dāng)，甚至略大于同相振動(dòng)，這與第1節(jié)中的理論計(jì)算結(jié)果相符合.

試驗(yàn)結(jié)果表明：在主跨支撐特性相近時(shí)，勵(lì)磁機(jī)不平衡主要激起主跨兩端同相振動(dòng)，二階不平衡主要激起反相振動(dòng)；當(dāng)主跨支撐特性相差較大時(shí)，不論是發(fā)電機(jī)二階不平衡還是勵(lì)磁機(jī)的不平衡，都將激起主跨兩端較大的同相和反相振動(dòng).此試驗(yàn)進(jìn)一步驗(yàn)證了理論模擬結(jié)果的可靠性.

3 結(jié) 論

（1）發(fā)電機(jī)前瓦支撐剛度不足時(shí)，不論是發(fā)電機(jī)二階還是勵(lì)磁機(jī)不平衡都將激起較大的同相和反相振動(dòng)，且各種形式的不平衡在其對(duì)應(yīng)的臨界轉(zhuǎn)速下同相和反相振動(dòng)都較大，避開臨界轉(zhuǎn)速后振幅大幅下降.

（2）發(fā)電機(jī)后瓦支撐剛度降低較多時(shí)，則發(fā)電機(jī)二階或勵(lì)磁機(jī)不平衡在發(fā)電機(jī)二階臨界轉(zhuǎn)速和勵(lì)磁機(jī)一階臨界轉(zhuǎn)速下都激起較大振動(dòng).

（3）發(fā)電機(jī)任何一端支撐剛度大幅下降后，發(fā)電機(jī)二階和勵(lì)磁機(jī)不平衡都將激起較大同相和反相振動(dòng)；而在發(fā)電機(jī)兩端支撐特性相近的情況下，勵(lì)磁機(jī)不平衡主要激起發(fā)電機(jī)兩端同相振動(dòng)，發(fā)電機(jī)二階不平衡主要激起反相振動(dòng).

［1］沈佩華，顧晃，任浩仁.關(guān)于引進(jìn)型300 MW 汽輪發(fā)電機(jī)組振動(dòng)異常問題的研究［J］.中國電機(jī)工程學(xué)報(bào)，2004，24（9）：267-271. SHEN Peihua，GU Huang，REN Haoren.A research of the vibration malfunction problem for imported type 300 MW turbogenerator sets［J］.Proceedings of the CSEE，2004，24（9）：267-271.

［2］李小軍，童小忠，李榮義，等.600 MW 超臨界機(jī)組軸系振動(dòng)分析診斷及處理［J］.汽輪機(jī)技術(shù)，2009，51（1）：70-72. LI Xiaojun，TONG Xiaozhong，LI Rongyi，etal.Analysis diagnosis and treatment of vibration for 600 MW supercritical units［J］.Turbine Technology，2009，51（1）：70-72.

［3］何國安，閔昌發(fā)，張學(xué)延，等.國產(chǎn)600MW 汽輪發(fā)電機(jī)組軸系動(dòng)平衡研究［J］.動(dòng)力工程學(xué)報(bào)，2012，32（4）：282-288. HE Guoan，MIN Changfa，ZHANG Xueyan，etal.Dynamic balancing of the shaft system for a domestic 600 MW turbo-generator set［J］.Journal of Chinese Society of Power Engineering，2012，32（4）：282-288.

［4］NICHOLAS J C，BARRET L E.The effect of support flexibility on critical speed prediction［J］.ASLE Trans-actions，1986，29（3）：329-338.