具有參數區間不確定的協調器保性能優化

石海軍,錢林方,李淼

(1.南京理工大學機械工程學院,江蘇南京 210094;

2.南京南瑞集團公司智能化電氣設備研發中心,江蘇南京 211100）

具有參數區間不確定的協調器保性能優化

石海軍1,2,錢林方1,李淼1

(1.南京理工大學機械工程學院,江蘇南京 210094;

2.南京南瑞集團公司智能化電氣設備研發中心,江蘇南京 211100）

為了解決協調器優化設計中的不足,提出了基于參數區間不確定分析的保性能優化方法。該方法考慮工程設計中關鍵尺寸或材料參數變化的區間性,通過將參數區間變化從參數變差空間映射到目標和約束空間,得到的目標和約束性能退化估計作為原優化問題的附加約束,形成外層、內層的優化結構。某火炮協調器的優化結果證明了該方法在解決具有參數區間不確定的復雜工程優化問題上的有效性。

兵器科學與技術;區間不確定;保性能優化;協調器

0 引言

傳統優化設計是基于確定性模型的,即材料特性、載荷、幾何尺寸、元器件參數等在優化過程中不存在攝動影響。然而在實際工程問題中,這些參數或多或少會受到外界干擾而產生攝動,進而影響設計的優化目標性能或改變約束的可行性[1-2]。近年來,針對參數不確定性問題,國內外學者提出了許多方法。一般而言,這些方法基于兩類模型:概率模型和非概率模型。在基于概率的模型中,參數的不確定性由概率密度函數來描述。與之對應的優化問題是在規定的失效概率下最小化設計成本(即可靠性設計優化)[3-4]或者同時最小化目標函數均值和結構響應方差(即魯棒設計優化)[5-6]。由于基于概率模型的優化能夠得到高置信度和高魯棒性的設計,所以它成為結構魯棒設計的有力工具。盡管概率模型提供了魯棒設計的有效框架,但是值得注意的是,它有時很依賴于不確定參數的精確概率分布信息,然而這些信息在實際工程設計問題中很難或不可能獲得。與概率不確定模型不同,非概率模型只需要假設不確定參數的變化范圍,不要求統計學意義上的概率分布信息[7-10]。由于實際產品在設計和加工過程中,均給定一個確定的公差尺寸,而不是一個確定的概率分布,故而基于參數區間不確定模型的研究很有實際意義。

本文針對某中口徑火炮協調器的傳統優化解不能滿足設計要求的問題,提出了基于參數區間不確定的保性能優化方法。通過該方法得到的魯棒解,在系統參數存在區間不確定的情況下,仍然滿足設計要求。

1 協調器優化問題描述

圖1 某火炮協調器機電液一體化模型Fig.1 Integrative model of mechanics-electronics-hydraulics of a shell transfer arm

火炮協調器是自行火炮供輸彈系統的一個重要部件,是連接彈倉與輸彈器、藥倉與輸藥器的紐帶,其作用是負責從彈倉和藥倉中接受彈丸和裝藥模塊,將它們傳輸到炮尾后部,并實現與炮膛軸線的對齊,經輸彈機和輸藥機把彈丸和模塊藥分別可靠、一致地推入藥室[11]。協調器由機械臂、液壓系統和電氣控制系統組成,是一個典型的機電液控系統,如圖1所示。轉換電路、控制器、信號放大電路等,其作用是根據期望輸入對液壓及機械子系統進行控制;機械子系統包括液壓缸本體、協調臂本體及彈丸抱夾機構,負責執行液壓輸出,完成預期的協調任務;液壓子系統由液壓泵、蓄能器、伺服閥及其他輔件組成,主要對電氣控制信號作出響應,驅動液壓缸動作。協調器存在多個設計變量,本文主要考慮PD控制器的比例增益Kp、微分增益Kd、傳感器增益Ka、功率放大器增益Kf、液壓缸內徑D、活塞桿直徑d、協調臂上液壓缸活塞支點位置L,其中D和d取離散值。

1.1 協調器模型

1)電氣控制器模型。電氣控制系統通過安裝在協調臂轉軸上的角位移傳感器檢測到協調臂當前轉角信號θ,經模數轉換,結合期望轉角θd,則轉角誤差e=Kaθ-θd.然后通過PD控制器,輸出控制電流,經功率放大器放大,得到電流控制信號控制液壓系統作動。其工作原理如圖2所示。則電氣控制輸出為

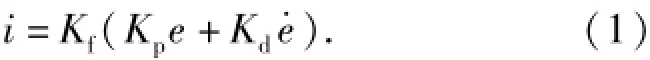
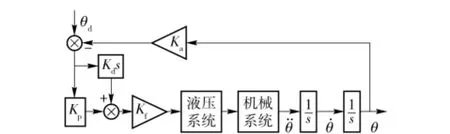
圖2 PD控制回路Fig.2 PD controller

2)液壓伺服閥模型。液壓系統中由于存在蓄能器和溢流回路,所以假設供油壓力基本保持不變。伺服閥的輸入為閥芯的位移,其流量qL與閥芯位移xs之間的關系為

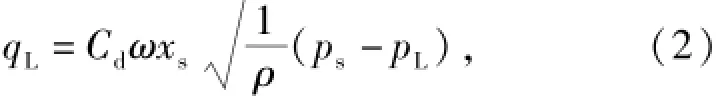
式中:ω=πd,d為閥芯凸肩直徑;xs=Ksi,Ks為伺服閥增益,i為輸入電流;Cd為流量系數;ρ為油液密度;ps為供油壓力;pL為液壓缸工作壓力,其值由工作負載決定。

3)液壓缸模型。液壓缸為機械系統的執行元件,輸入為油液壓力,輸出為活塞桿速度,如圖3所示。

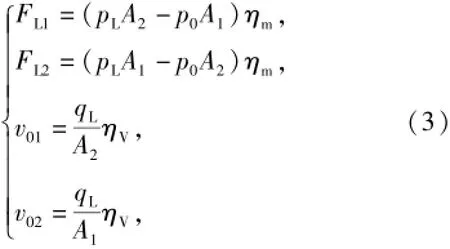
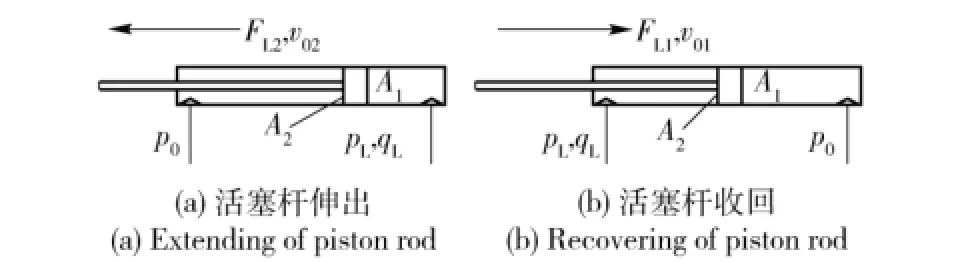
圖3 液壓缸模型分析Fig.3 Analytical model of hydraulic cylinder

4)機械臂本體動力學模型。機械臂在液壓缸活塞桿B點驅動下,繞點A旋轉,液壓缸與機械臂所成夾角為α,FL為液壓缸負載,即作用在協調臂上的驅動力;v0為液壓缸活塞輸出速度,當活塞桿伸出時v0=v02,反之v0=v01.設機械臂質量為m,轉動慣量為J,質心距點A的距離為L,機械臂轉角為θ,其他參數如圖4所示。分析可知機械臂上B點的速度為

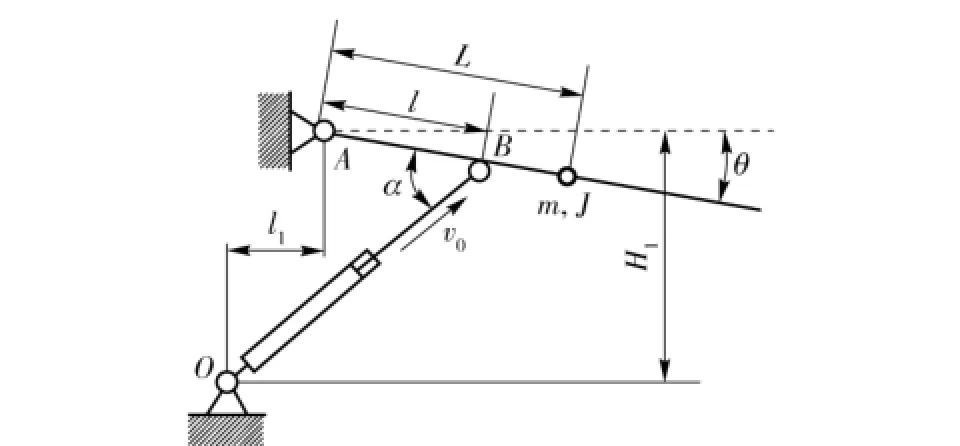
圖4 機械臂本體模型Fig.4 Mechanical arm model

則液壓缸負載為

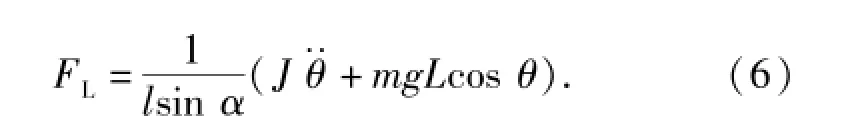
1.2 優化的數學模型

為了使液壓缸活塞桿在整個協調過程中受力均衡分布,協調器設計要求在超調量不超過σ0,上升時間不超過0.5 s的約束條件下,最小化液壓缸活塞桿受力的最大值,由于力存在方向性,故而取標量(其絕對值的最大值)作為目標。其數學模型如下:

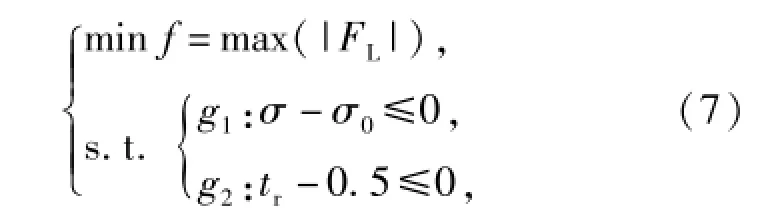
式中:σ0為允許的超調量,σ0=1.5%;tr為上升時間。

1.3 不確定問題

按照(7)式的優化模型進行仿真分析,優化結果如表1所示,求得的目標函數值為6 670 N,約束函數值分別為-0.136、-0.014.可以看出約束g1、g2均為有效約束。但是在實際生產和使用過程中,存在許多不確定因素,如隨溫度變化的傳感器增益、放大器增益、裝配誤差等。本文考慮Ka、Kf、L及ps這4個設計變量和參數存在攝動,且攝動幅值分別為0.005、0.005、3 mm和0.2 MPa,利用Matlab隨機生成按正態分布規律的20組攝動數據。模擬系統參數的不確定性,分析結果如圖5～圖7所示。圖5是20組隨機攝動下活塞桿的受力相對優化結果的偏差,圖6、圖7分別為兩個約束函數在攝動數據下與優化結果中的約束值之間的偏差,虛線為約束的最大退化許可值。

表1 設計優化結果Tab.1 Results of design optimization

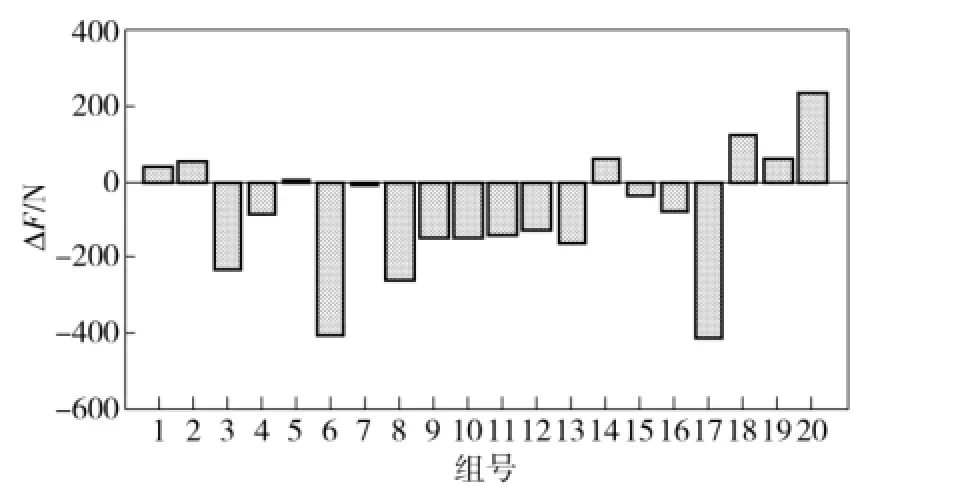
圖5 隨機攝動對活塞桿受力的影響Fig.5 The effect of random perturbation on force applied on piston rod

可以看出,在參數不確定的情況下,活塞桿受力出現波動,最大增加了約300 N,同時系統出現了違背約束g1、g2的情況,即在實際生產過程中,按照給定的設計公差加工或裝配出的協調器不能完全滿足設計要求,故而必須考慮參數區間不確定對系統性能的影響。

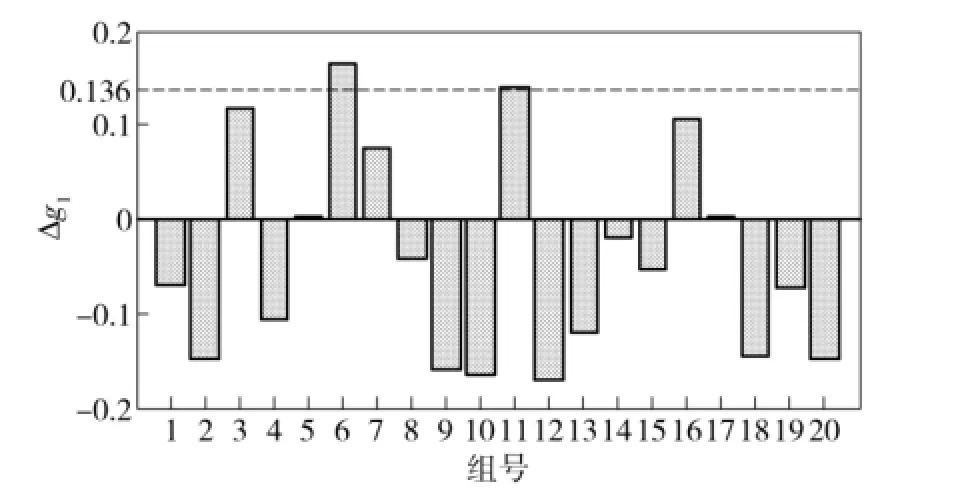
圖6 隨機攝動對約束g1的影響Fig.6 The effect of random perturbation on the constraint g1

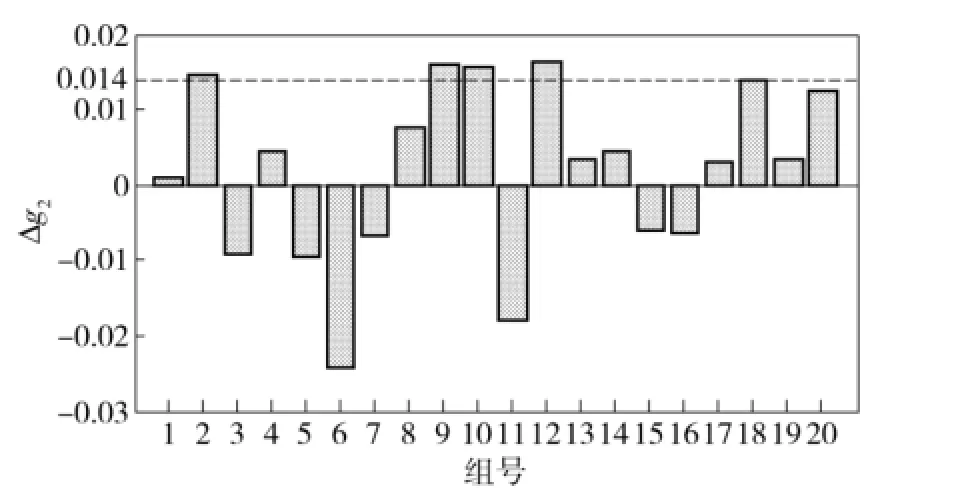
圖7 隨機攝動對約束g2的影響Fig.7 The effect of random perturbation on the constraint g2

2 參數區間不確定的保性能優化

2.1 參數區間不確定保性能優化

對于設計變量標稱值x0及參數標稱值p*,對應的目標函數及約束函數標稱值用f0、g0表示,參數p (包括不確定的設計變量)變化下界、上界分別為pL和pU,對應的目標函數變化為Δf,圖8所示以2個不確定參數與2個目標函數為例,圖8(a)所示參數為線性相關,本文所提方法同樣適用非線性情況。從圖中可以看出,在參數存在不確定的情況下,目標函數性能可能會出現“退化”現象,約束函數與目標函數相似,也會出現類似退化,對于起作用的約束,可能會出現違背原始約束的情況。

為此人為規定一個可接受的目標退化域Δfk,0(AODR),如圖8(b)所示,若目標函數的性能變化范圍在AODR內,那可以認為優化解可以接受。于是對于具有望小特性的目標函數,設計點的最大退化估計可表示為

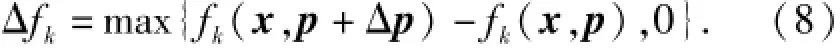
對于望目特性的目標函數,可采用原函數的付函數構造新目標函數,則新目標函數具有望小特性,完全可由(8)式求得;對于望目特性的目標函數,其最大退化估計可表示為

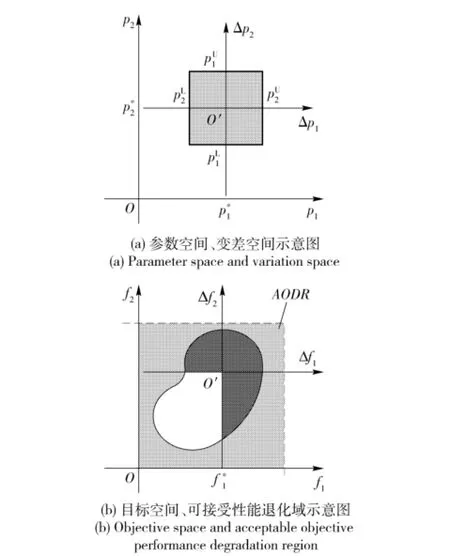
圖8 參數空間、目標空間Fig.8 Parameter space and objective space

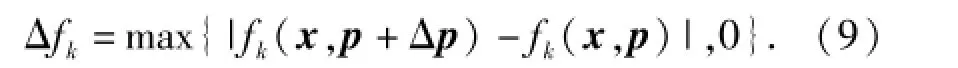
以具有望小特性的目標函數為例,設計點對性能滿足的程度用目標性能退化指標Rf描述

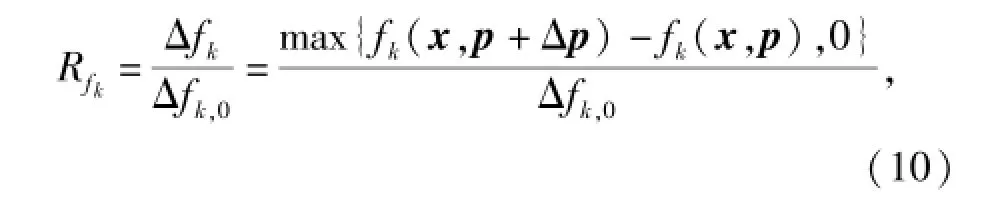
式中:0≤k≤K,K為目標函數個數。可見,當Rf≤1時,目標函數性能變化區域在AODR內,解滿足設計要求。

與目標性能退化估計類似,假設在點x約束函數可行,即gm(x,p)＜0,0≤m≤M,M為約束函數個數。此時約束函數可接受的最大退化Δgm,0= |gm(x,p)|,那么約束可行性的最大退化估計Δgm和退化指標Rgm可以表示為

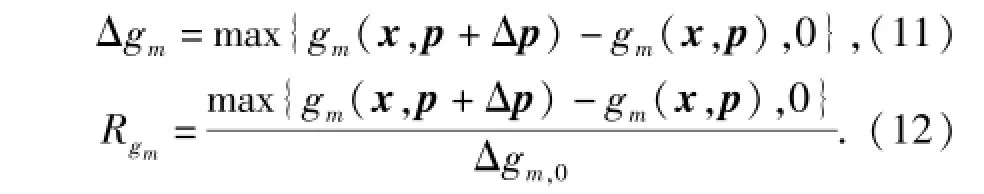
若所有的目標性能和約束可行性的靈敏度區域均在可接受性能退化范圍內,那么設計優化結果滿足性能優化條件,用性能優化指標R來描述,則也即,將性能優化指標R≤1作為原優化問題的一個附加約束,那么即使存在不確定因素,優化結果也必定滿足設計要求。

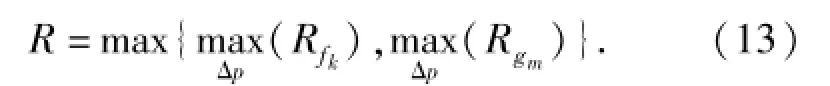
(10)式和(12)式所示的性能優化指標可以變換為

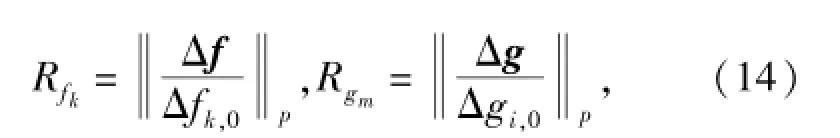
式中:p取∞,即表示無窮大范數。擴展而言,也可根據具體情況取p=1(1-范數)或2(2-范數)來作為性能優化指標的一種度量。

2.2 數學模型

由于不確定參數及變量的存在,(7)式所描述的優化模型變為如下形式:

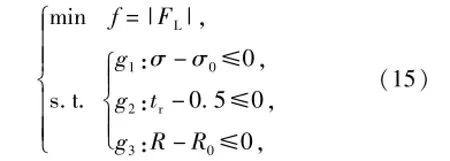
式中:R由(13)式給出;R0為決策者期望的魯棒程度。這樣,(7)式所描述的優化模型就轉變為內層優化求R的極大值、外層優化求原目標函數極小值的問題,如圖9所示,其中K=1,M=2.

圖9 性能魯棒優化的雙層優化框架Fig.9 Double-layer framework of performance robustness

3 優化結果分析

由于模型復雜,計算量較大,為了提高計算效率,本文采用徑向基函數(RBF)近似技術構建計算模型。外層優化采用進化計算算法,最大進化代數取400,內層優化采用非線性規劃。于是對(15)式給出的魯棒優化模型進行求解,其優化結果在表2中給出,求得的目標函數值為9 150 N,約束函數值分別為-0.4、-0.021.

為了和傳統優化結果進行對比,采用相同的攝動數據進行分析,其結果如圖10～圖12所示。圖10為重新優化后在攝動數據下活塞桿受力相對優化結

表2 設計優化結果Tab.2 Results of guaranteed cost optimization

果的變化情況,圖11、圖12分別為2個約束函數在攝動數據下與優化結果中的約束值之間的偏差,虛線為約束退化的最大限制。從圖中可以看出,在攝動存在的情況下,原優化結果使得活塞桿受力特性變差,最大高出設計標稱值約300 N,而經保性能優化后,活塞桿受力均得到改善,只有極少部分會超出設計標稱值,最大增加約100 N,同樣優于原設計;約束函數g1、g2的值在標稱值上下變化,但是均未超出其最大限制,說明該方法能夠有效解決具有參數區間不確定的協調器優化問題。

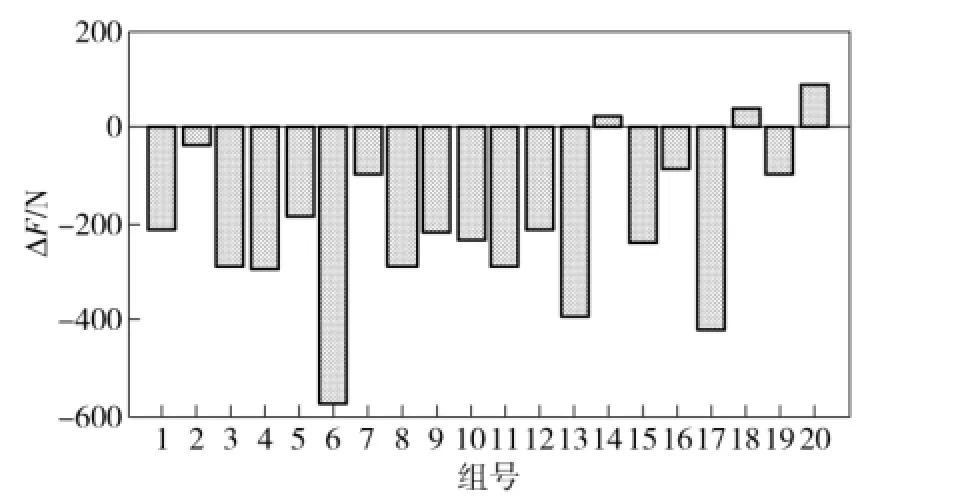
圖10 活塞桿受力在攝動數據下的變化Fig.10 Variation of force applied on piston rod with perturbed data

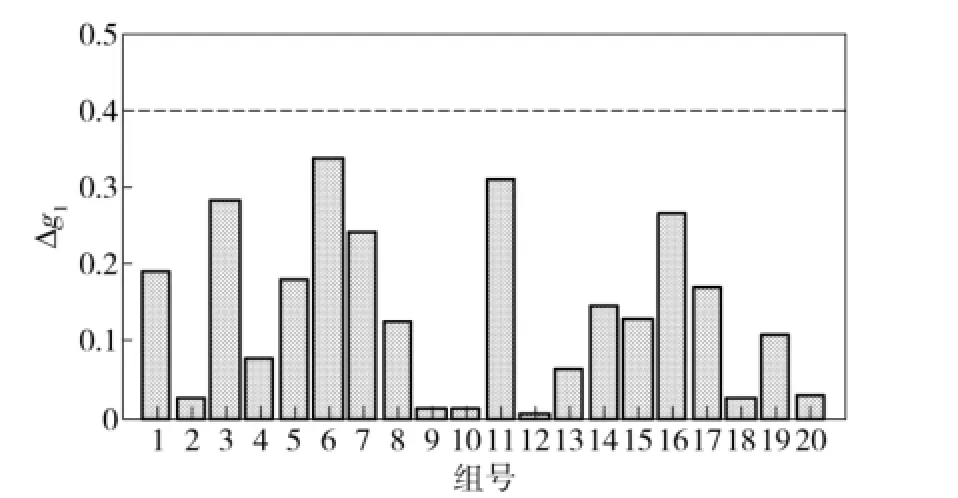
圖11 約束g1在攝動數據下的變化Fig.11 Variation of the constraint g1with perturbed data

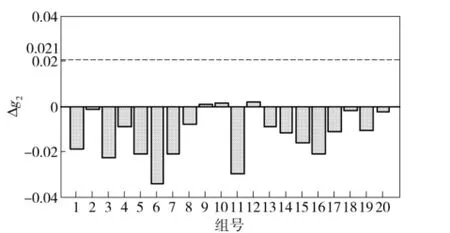
圖12 約束g2在攝動數據下的變化Fig.12 Variation of the constraint g2with perturbed data

通過以上分析可知,本文提出的保性能優化方法可以保證目標函數性能不退化,同時也能夠使優化解在參數區間不確定存在的情況下具有良好的魯棒性。

4 結論

由于實際工程設計及生產過程中,零部件的加工與裝配尺寸均用精度公差配合來表示的;在使用過程中,環境溫度的變化、電子元器件的特性變化也是區間變化的。傳統的設計優化方法針對的是確定型優化模型,所以求得的設計解不能完全滿足原始設計要求;而基于概率模型的優化方法需要較精確的概率分布信息,在火炮武器裝備使用及管理過程中較難獲取。本文從參數區間變化的角度出發,將參數區間變化從參數變差空間映射到目標和約束空間,得到的目標和約束性能退化估計作為原優化問題的附加約束,形成雙層優化結構。通過某火炮協調器設計優化的對比分析,可以看出,在解決具有參數區間不確定的復雜工程優化問題上,該方法有很好的應用參考價值。

References)

[1] Lin X X,Janak S L,Floudas C A.A new robust optimization approach for scheduling under uncertainty:Ⅰ.bounded uncertainty [J].Computers and Chemical Engineering,2004,28(6/7): 1069-1085.

[2] Beyer H G,Sendhoff B.Robust optimization-a comprehensive survey[J].Computer Methods in Applied Mechanics and Engineering,2007,196(33/34):3190-3218.

[3] Du X X,Huang B Q.Reliability-based design optimization with equality constraints[J].International Journal for Numerical Methods in Engineering,2007,72(11):1314-1331.

[4] Lee I,Choi K K,Du L,et al.Dimension reduction method for reliability-based robust design optimization[J].Computers and Structures,2008,86(13/14):1550-1562.

[5] Shin S,Samanlioglu F,Cho B R,et al.Computing tradeoffs in robust design:perspectives of the mean squared error[J].Computers&Industrial Engineering,2011,60(2):248-255.

[6] 郭惠昕,岳文輝.含間隙平面連桿機構運動精度的穩健優化設計[J].機械工程學報,2012,48(3):75-81.

GUO Hui-xin,YUE Wen-hui.Design optimization of planar linkage mechanism with joint clearance for improving the robustness of kinematic accuracy[J].Chinese Journal of Mechanical Engineering,2012,48(3):75-81.(in Chinese)

[7] Li M,Azarm S,Boyars A,et al.A new deterministic approach using sensitivity region measures for multi-objective robust and feasibility robust design optimization[J].Journal of Mechanical Design,2005,128(4):874-883.

[8] 張曙光.不確定結構分析及優化中的區間模型[J].長春工程學院學報:自然科學版,2009,10(3):1-3.

ZHANG Shu-guang.Interval model of uncertain structure analysis and optimization[J].Journal of Changchun Institute of Technology:Natural Science Edition,2009,10(3):1-3.(in Chinese)

[9] 董榮梅,孫偉,許煥衛.基于區間分析的非概率穩健優化設計[J].大連理工大學學報,2011,51(1):51-55.

DONG Rong-mei,SUN Wei,XU Huan-wei.Non-probabilistic robust optimization design based on interval analysis[J].Journal of Dalian University of Technology,2011,51(1):51-55.(in Chinese)

[10] 李方義,李光耀,鄭剛.基于區間的不確定多目標優化方法研究[J].固體力學學報,2010,31(1):86-92.

LI Fang-yi,LI Guang-yao,ZHENG Gang.Uncertain multi-objective optimization method based on interval[J].Chinese Journal of Solid Mechanics,2010,31(1):86-92.(in Chinese)

[11] 侯保林,樵軍謀,劉琮敏.火炮自動裝填[M].北京:兵器工業出版社,2010:13.

HOU Bao-lin,QIAO Jun-mou,LIU Cong-min.The autoloader for self-propellant howitzer[M].Beijing:The Publishing House of Ordnance Industry,2010:13.(in Chinese)

Guaranteed Cost Optimization for the Shell Transfer Arm with Interval Uncertainty

SHI Hai-jun1,2,QIAN Lin-fang1,LI Miao1
(1.School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,Jiangsu,China;
2.Intelligent Electrical Equipment R&D Center,Nanjing NARI Group Co.Ltd.,Nanjing 211100,Jiangsu,China)

A guaranteed cost optimization method based on analysis of parameter interval uncertainties is proposed to overcome the disadvantage in design optimization of shell transfer arm.In this proposed method,the interval characteristic of key dimensions or material parameters in the engineering design is considered,and the parameter perturbations are mapped from variation space into objective and constraint spaces,then the obtained degraded-estimation of objective and constraint is acted as an additional constraint of original optimization problem,resulting in a new robust optimization of an outer-inner optimization structure.The optimization results of shell transfer arm show that the proposed method is effective in solving complex engineering optimization problems with interval uncertainties.

ordnance science and technology;interval uncertainty;guaranteed cost optimization;shell transfer arm

TP 301;TP18

:A

1000-1093(2014)02-0152-06

10.3969/j.issn.1000-1093.2014.02.002

2013-04-19

國家基礎科研計劃項目(A2620110003)

石海軍(1986—),男,博士研究生。E-mail:opt_bingo@163.com;錢林方(1961—),男,教授,博士生導師。E-mail:lfqian@vip.163.com