大定源瞬變電磁均勻?qū)訝罱橘|(zhì)正演計(jì)算

柳建新，張 維*，曹創(chuàng)華，蔡 盛

(1．中南大學(xué) 地球科學(xué)與信息物理學(xué)院，長沙 410083；2．有色資源與地質(zhì)災(zāi)害探查湖南省重點(diǎn)實(shí)驗(yàn)室，長沙 410083；3．中南大學(xué) 地質(zhì)調(diào)查研究院，長沙 410083)

0 引言

瞬變電磁法的主要工作裝置有中心回線、重疊回線、大定源回線等，其中又以大定源回線裝置應(yīng)用最為廣泛[1-2]。大回線源裝置的工作方法是采用較長的發(fā)送回線,利用階躍波電流場源激勵,在大地產(chǎn)生過渡過程場,斷電瞬間在大地中形成渦旋交變電磁場。在回線內(nèi)外一定的范圍內(nèi),可觀測到這種由地下介質(zhì)產(chǎn)生的二次感應(yīng)電磁場,隨時間變化的衰減特性,進(jìn)而從測量得到的異常信號中分析出地下不均勻體的導(dǎo)電性能和位置,以達(dá)到解決地質(zhì)問題的目的。大回線裝置與目標(biāo)體具有最佳耦合、異常幅值大、形態(tài)簡單、受旁側(cè)地質(zhì)體影響小的特點(diǎn),并對高阻層有很強(qiáng)的穿透能力,對低阻層有較高的分辨能力。這種裝置對鋪設(shè)回線的要求不是很嚴(yán)格,一旦鋪好回線后,不僅可采用多臺接收機(jī)同時工作,而且可以把接收線圈排成陣列,發(fā)展成陣列式接收的觀測系統(tǒng)。這種場源具有發(fā)射磁矩大、場均勻及隨距離衰減慢等特點(diǎn),適合于密集點(diǎn)距采樣,精細(xì)探測。

大回線由于面積較大，不能看作磁偶極子。因此，研究大回線源激發(fā)的電磁場有著重要的意義。國內(nèi)、外對大回線源產(chǎn)生電磁場的研究并不多，翁愛華[3]等首先求出任意一層電磁波的反射系數(shù)和透射系數(shù)，然后據(jù)此計(jì)算了圓形發(fā)射回生的頻率域電磁場；M. Poddar[4]根據(jù)電磁學(xué)互易原理和垂直磁偶源產(chǎn)生的電磁場；求解出距形發(fā)射回線產(chǎn)生的頻率域電磁場；Nagendra Partap Singh等[5]利用超幾何分布函數(shù)，化簡了圓形發(fā)射回線電磁場表達(dá)式中貝塞爾函數(shù)的乘積，從而求解出頻率域電磁場。

作者從基本的電磁場理論出發(fā)，給出大回線發(fā)射源框內(nèi)外不同位置的電磁響應(yīng)表達(dá)式，利用一種新的算法計(jì)算電磁響應(yīng)，并與傳統(tǒng)的線性數(shù)值濾波法計(jì)算結(jié)果進(jìn)行了對比分析(對比所用的濾波權(quán)系數(shù)，采用Anderson 計(jì)算的801個系數(shù))。

1 理論基礎(chǔ)

ε算法是一種遞歸方法，主要是基于以下三組關(guān)系式[7-8]：

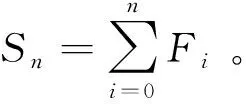
每個區(qū)間上的積分，采用以下形式計(jì)算：

式中m是積分階數(shù)；w是與橫坐標(biāo)x有關(guān)的權(quán)重向量。

通過對上述方程做簡單的變換，可以變換成與FHT算法一樣的形式：

2 回線源瞬變電磁響應(yīng)理論分析

圖1為大回線源瞬變電磁法工作裝置圖。置于地表的發(fā)送線框激發(fā)的階躍波，會在地下形成渦流場，回線電流的通斷過程中，在回線內(nèi)的磁通量會發(fā)生變化，通過分析接收線框接收到的磁通量變化信息，可以獲知地下介質(zhì)的分布情況。

圖1 大定源回線瞬變電磁工作布置示意圖Fig．1 Working schematic of transient electromagnetic method in large loop source

在層狀介質(zhì)情況下，由階躍電流激發(fā)，在發(fā)送線框內(nèi)任意位置接收的頻率域電磁響應(yīng)為[9]：

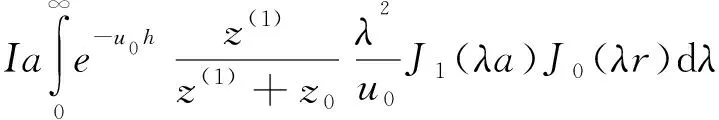
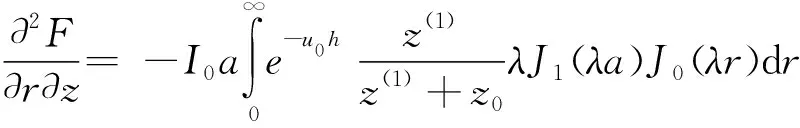
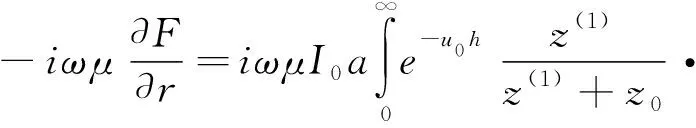
其中Hr(ω)、Eφ(ω)為徑向的磁場分量和電場分量；Hz(ω)為垂向磁場分量；a是回線等效半徑；I是發(fā)送電流；z0是表層阻抗；z(1)是總的波阻抗；h為發(fā)送線框距地面高度；r為發(fā)送線圈中心點(diǎn)與接收線框中心點(diǎn)之間的距離。波阻抗由以下公式計(jì)算[10]得到：

Hn為層狀介質(zhì)第n層的厚度。

z(n)=znzj=-iωμ0/uj

z0=-iωμ0/u0=-iωμ0/λ

3 計(jì)算結(jié)果分析

計(jì)算都是基于均勻?qū)訝罱橘|(zhì)模型進(jìn)行的。ρ1=100 Ω·m，ρ2=1 000 Ω·m，a=100 m，H=40 m，發(fā)送電流為I=1 A，發(fā)送頻率為f= 25 Hz。

圖2和圖3描述了積分核函數(shù)的收斂情況。由圖2可知，對于h= 0 m的情況，零階和一階的第一類貝塞爾函數(shù)在λ增大的時候，振蕩很明顯，這是貝塞爾函數(shù)本身的性質(zhì)。除去貝塞爾函數(shù)之后，核函數(shù)剩余部分的虛部是單調(diào)遞減的，而實(shí)部則是單調(diào)遞增的。在h= 5 m 時(圖3)，除去貝塞爾函數(shù)之后的核函數(shù)虛部仍然是單調(diào)遞減的，而實(shí)部則是隨λ增大而增大，達(dá)到一個最大值后開始隨λ增大而減小。

由Anderson 的研究可知，在利用快速漢克爾變換計(jì)算貝塞爾函數(shù)積分的時候，積分核函數(shù)(除去貝塞爾函數(shù))必須是單調(diào)遞減的。所以對于h= 0 m的情況，用漢克爾變換不能得到穩(wěn)定的解(圖4)。

對于垂向磁場實(shí)部的計(jì)算：在h= 0 m時(圖4)，利用FHT算法得到的結(jié)果跳動比較厲害，而且在r>a時，計(jì)算結(jié)果誤差較大，而用QWE法得到的結(jié)果除了在r= 100 m附近出現(xiàn)一個極大值外，在框內(nèi)、外的計(jì)算結(jié)果都比較穩(wěn)定；在h= 5 m時(圖5)，兩種方法的計(jì)算結(jié)果曲線趨勢是一樣的，不過用QWE算法得到的計(jì)算結(jié)果相對較穩(wěn)定。對于虛部的計(jì)算，兩者的計(jì)算結(jié)果吻合的都非常好。通過上面的分析可知，這是因?yàn)楹撕瘮?shù)的虛部是收斂，所以利用FHT算法計(jì)算能得出比較精確的結(jié)果。

此外，由于QWE計(jì)算積分時的求積點(diǎn)是不均勻分布的一些高斯積分點(diǎn)，計(jì)算的核函數(shù)的數(shù)量是隨r的變化而變化的，而數(shù)值濾波法由于濾波權(quán)系數(shù)數(shù)量是固定的(801個)，所以計(jì)算的核函數(shù)的數(shù)量是不隨r變化的。由圖6可以看出，對于大多數(shù)的r，用QWE算法所需計(jì)算的核函數(shù)數(shù)量都是少于用FHT算法的。

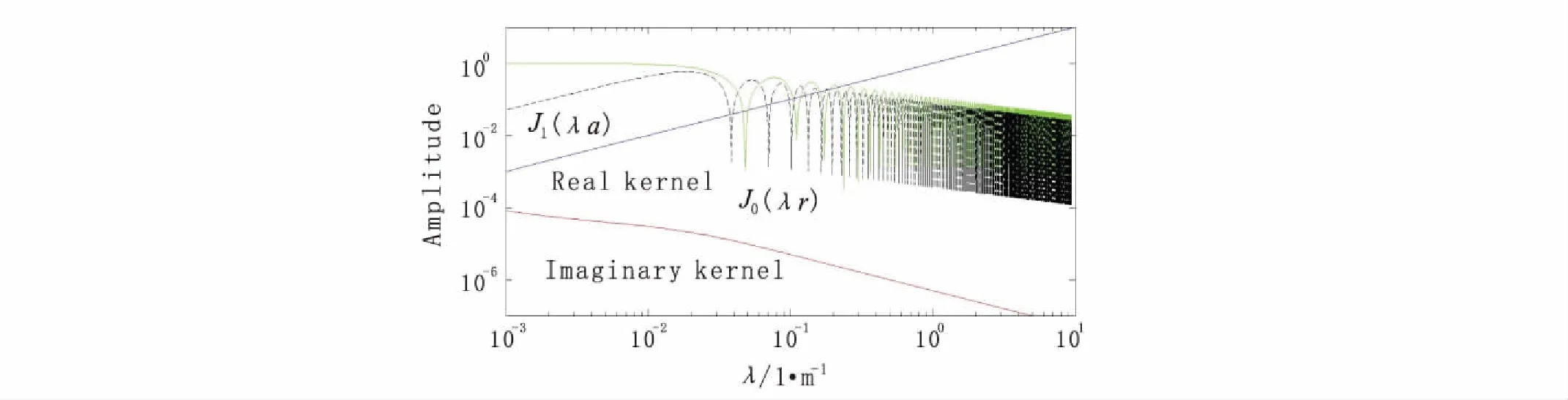
圖2 r =50 m，h =0 m 時，積分核函數(shù)(不含貝塞爾函數(shù))及貝塞爾函數(shù)性質(zhì)Fig．2 Characteristics of kernel functions (without the Bessel functions) and Bessel functions when r =50m, h=0 m

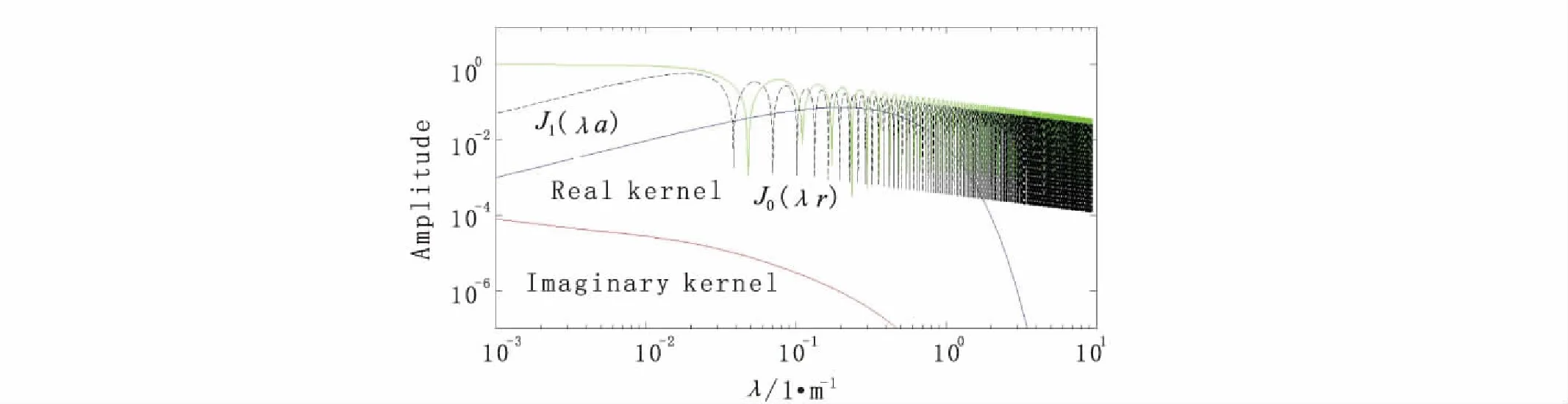
圖3 r =50 m，h =5 m 時，積分核函數(shù)(不含貝塞爾函數(shù))及貝塞爾函數(shù)性質(zhì)Fig．3 Characteristics of kernel functions (without the Bessel functions) and Bessel functions when r =50 m, h =5 m

圖4 h=0 m時，兩種方法在不同偏移距條件下實(shí)部和虛部響應(yīng)對比圖Fig．4 Comparison of real and imaginary responses by each method in different offset, h=0 m

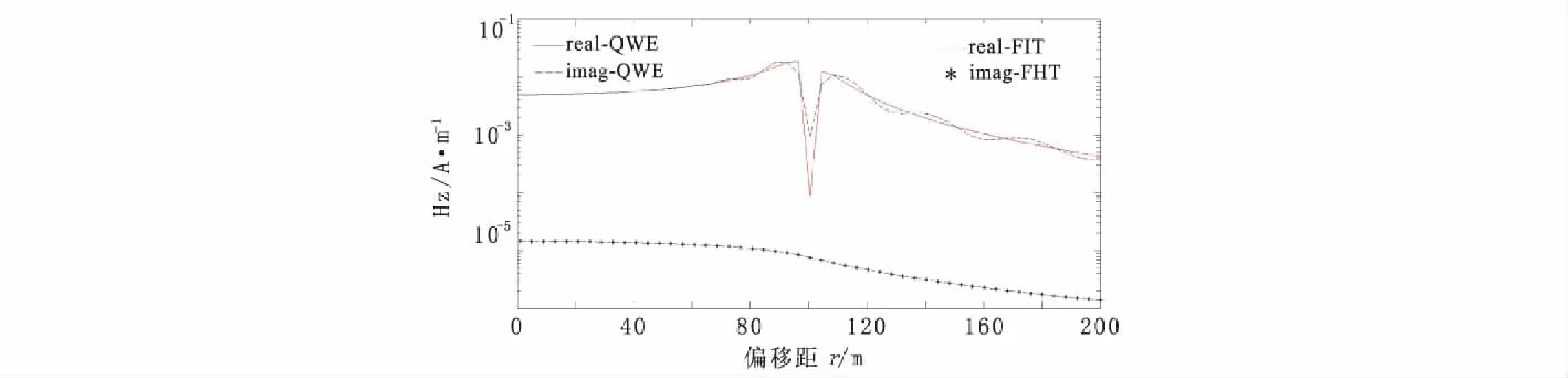
圖5 h = 5 m時，兩種方法在不同偏移距條件下實(shí)部和虛部響應(yīng)對比圖Fig．5 Comparison of real and imaginary responses by each method in different offset, h=5 m

4 結(jié)論

作者對大回線源瞬變電磁法一維層狀正演算法進(jìn)行了研究，將QWE方法與傳統(tǒng)的基于快速漢克爾變換的數(shù)字濾波法進(jìn)行了比較：兩者對于虛部的計(jì)算吻合比較好；然而對于實(shí)部的計(jì)算，QWE算法計(jì)算的結(jié)果相對較穩(wěn)定，尤其是對于線框位于地表的情況，F(xiàn)HT算法對于不同偏移距的計(jì)算結(jié)果變化較大，而QWE算法的結(jié)果比較穩(wěn)定；此外QWE算法所需計(jì)算的核函數(shù)數(shù)量隨偏移距的不同是不斷變化的，在大多數(shù)偏移距條件下，所需計(jì)算的核函數(shù)數(shù)量均少于數(shù)字濾波法。

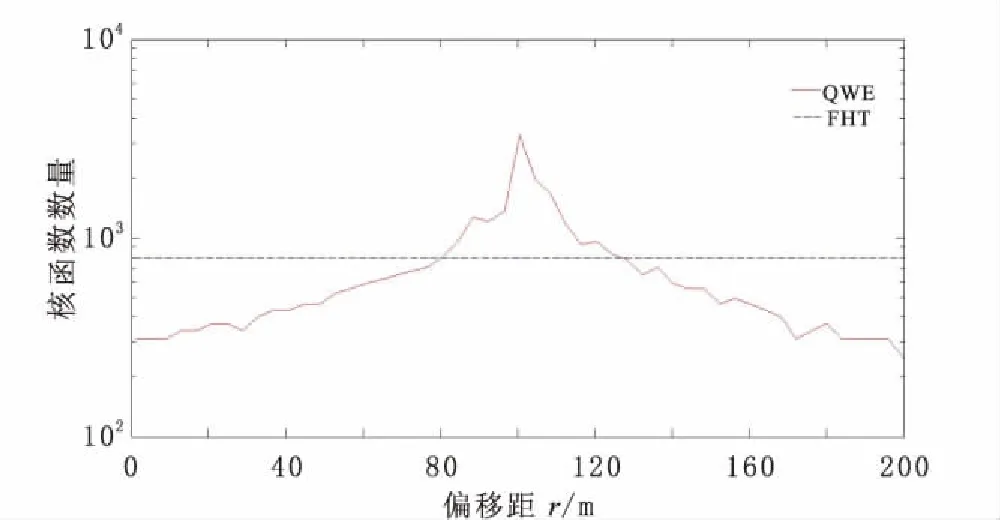
圖6 h =0 m時，兩種方法不同偏移距條件下核函數(shù)計(jì)算數(shù)量對比Fig．6 Comparison of the number of kernels evaluations required by each method in different offset

參考文獻(xiàn)：

[1] 薛國強(qiáng), 秦克章, 黃樹峰,等.大回線源瞬變電磁技術(shù)在西藏山南地區(qū)探礦中的應(yīng)用[J].地質(zhì)與勘探,2011, 47(1):100-106.

[2] 徐貴東, 黃繼軍, 劉德軍,等.瞬變電磁在吉林省紅旗嶺銅鎳礦勘查中的應(yīng)用[J].吉林地質(zhì), 2010, 29(4): 79-82.

[3] 翁愛華,李舟波,王雪秋.地表大回線源在任意層狀介質(zhì)中產(chǎn)生磁場的計(jì)算[J].物探化探計(jì)算技術(shù), 2000, 22(3):245-248.

[4] PODDARM A. Rectangular Loop Source of Current on a Two-layered Earth[J]. Geophys,Prosp, 1982, 30:101-114.

[5] NAGENDRA PARTAP SINGH, TORU MOGI. Electromagnetic Response of a Large Circular Loop Source on a Layered Earth: A New Computation Method[J]. Pure and Applied Geophysics,2005, 162:181.

[6] LONGMAN I M. Note on a method for computing infinite integrals of oscillatory functions: Mathematical Proceedings of the Cambridge Philosophical Society[J].Mathematical proceedings of the Cambrige Philosophical Society,1956,52(4): 764-768.

[7] SHANKS D. Nonlinear transformations of divergent and slowly convergent sequences[D]．Journal of Mathematical Physics, 1955, 34：1-42.

[8] KERRY KEY.Is the fast Hankel transform fast than quadrature[J]．Geophysics, 2012,77(3): 21-30.

[9] 考夫曼A.A, 凱勒.G.V.頻率域和時間域電磁測深[M].北京:地質(zhì)出版社,1987.

[10] 牛之璉.時間域電磁法原理[M].長沙：中南大學(xué)出版社, 2007.

[11] ANDERSON W L. Fast Hankel-transfroms using related and lagged convolution[J]．ACM Transforms on Mathematical Software, 1982, 8(4)：344-368.

[12] GUPTASARMA D B. Singh. New digital linear filters for Hankel J(0)and J(1)transforms[J]. Geophysical Prospecting, 1997, 45:745-762.

[13] 方文藻,李予國,李貅.瞬變電磁測深法原理[M].西安:西北工業(yè)大學(xué)出版社,1993.

[14] 李貅.瞬變電磁測深的理論與應(yīng)用[M].西安：陜西科學(xué)技術(shù)出版社, 2002.

[15] 薛國強(qiáng),李貅,郭文波.大回線源瞬變電磁響應(yīng)[J].石油地球物理勘探,2007,42(5):586-590.

[16] CHAVE A D. Numerical integration of related Hankel transforms by quadrature and continued fraction expansion[J].Geophysics, 1983, 48:1671-1686.

[17] 劉繼東, 方文藻. 用線性數(shù)字濾波法計(jì)算大回線源在地下形成的瞬變電磁場[J].物探化探計(jì)算技術(shù), 1996, 18(4):231-237.

[18] 李建慧, 劉樹才, 李富,等.大定源瞬變電磁法矩形發(fā)射回線激發(fā)的電磁場[J]．物探化探計(jì)算技術(shù), 2008, 30(2):154-157.