一種描述放射性氣體模型解的適定性擴(kuò)展

楊 麗

（濰坊醫(yī)學(xué)院公共衛(wèi)生學(xué)院，山東濰坊261053）

一種描述放射性氣體模型解的適定性擴(kuò)展

楊 麗

（濰坊醫(yī)學(xué)院公共衛(wèi)生學(xué)院，山東濰坊261053）

在新的初值條件下研究了一類雙曲與橢圓耦合系統(tǒng)解的適定性，并且將解空間在半群的意義下進(jìn)行擴(kuò)展，使此類系統(tǒng)解的適定性有了全新的意義和性質(zhì).同時(shí)利用該系統(tǒng)解的適定性，使用雙曲型伸縮技術(shù)，對松弛極限也進(jìn)行了討論.

守恒律方程；適定性；半群；松弛極限

1 預(yù)備知識

守恒律方程作為偏微分方程的重要組成部分一直是廣大數(shù)學(xué)工作者的重要研究內(nèi)容，它興起于20世紀(jì)50年代，可以說是一個(gè)新的研究領(lǐng)域.它在物理方面的應(yīng)用非常廣泛，幾乎所有連續(xù)力學(xué)的模型都是這種方程.本文的研究對象是一類雙曲和橢圓耦合系統(tǒng)的守恒律方程，它是描述放射性氣體運(yùn)動的歐拉方程的簡化，系統(tǒng)為［1－4］：

其中：（u，q）（x，t）為未知函數(shù)，f（u）是屬于C2的光滑函數(shù)，初值條件為u（x，0）＝u0（x），f（0）＝0.（x，t）∈（R，［0，＋∞））.方程ut＋f（u）x＋qx＝0是雙曲守恒律方程，方程－qxx＋q＋ux＝0是一個(gè)線性橢圓方程.這樣系統(tǒng)即為雙曲－橢圓耦合系統(tǒng).

下面將方程進(jìn)行轉(zhuǎn)化［5］，

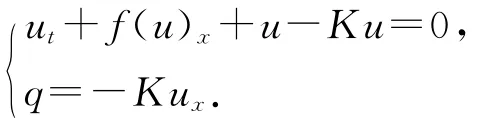
其中：q＝－Kux，qx＝－Kuxx＝u－Ku，K滿足

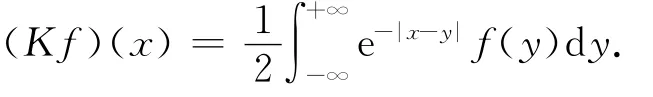
2 系統(tǒng)適定性已有的結(jié)果

考慮原系統(tǒng)轉(zhuǎn)化后的方程

其中f（u）是屬于C2的光滑函數(shù)，且

上述方程加粘性項(xiàng)后的方程為

其中μ≥0為粘性系數(shù).利用粘性系數(shù)消失法，當(dāng)初始條件u0∈L1（R）∩L∞（R）時(shí)，原系統(tǒng)的解具有下列性質(zhì)：

定理2.1［6－8］設(shè)u，ˉu∈L∞（［0，T］；L1（R）∩L∞（R））是方程（1.1）的弱熵解，對應(yīng)初值u0，ˉu0∈L1（R）∩L∞（R），則?t∈［0，T］有

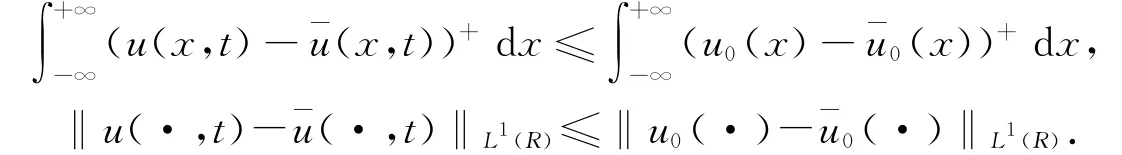
若u0（x）≤ˉu0（x），則

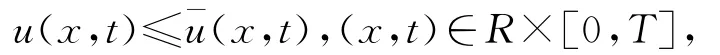
且u，ˉu∈［－a，a］.其中a＝max｛‖u0‖L∞（R），‖ˉu0‖L∞（R）｝.

推論2.1（解的唯一性） 方程（1.1）存在最多一個(gè)弱熵解u∈L∞（［0，T］；L1（R）∩L∞（R）），其中對應(yīng)初值u0∈L1（R）∩L∞（R）.

推論2.2 由解的唯一性知，方程（1.1）的任意熵解u∈L∞（［0，T］；L1（R）∩L∞（R））滿足估計(jì)式

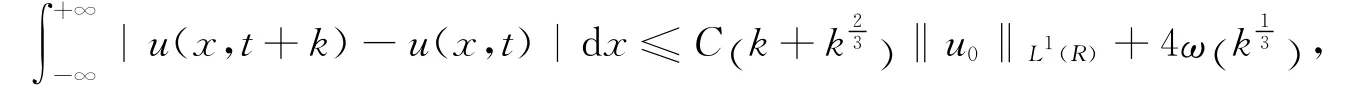
ω代表初值的L1連續(xù)模，且u∈C（［0，T］；L1（R）），其中T＞0.

3 系統(tǒng)適定性的擴(kuò)展

將初值u0∈L1（R）∩L∞（R）擴(kuò)展到u0∈L∞（R）.首先賦予新的范數(shù)‖｜·｜‖，令

其中φ（x）≥0，φ（x）∈C∞（R），滿足

如果定義方程（1.1）的解算子S（t）：t＞0，

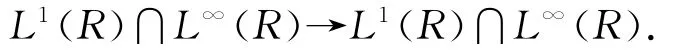
這樣方程（1.1）的解u（x，t）在初值u0（x）條件下可以表達(dá)為

且

總結(jié)上述關(guān)于方程（1.1）解的一系列性質(zhì)可以知道解算子S（t）滿足下面性質(zhì)：

（1）S（0）＝I.

（2）S（t＋τ）＝S（t）S（τ），?t，τ＞0.

（3）如果u0－ˉu0∈L1（R），則

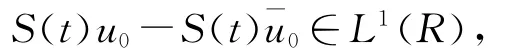
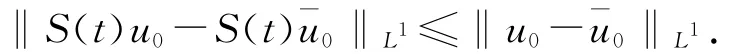
（4）如果u0≥ˉu0，?x∈R，則

（5）S（t）u0∈C（［0，＋∞）；L1（R））.

這樣解算子S（t）在空間L1（R）∩L∞（R）中形成了L1的壓縮半群，為把這個(gè)半群的定義空間擴(kuò)大至L∞，并且賦予（3.1）式所定義的范數(shù)，就需要證明S（t）在空間L1（R）∩L∞（R）中按范數(shù)‖｜·｜‖是連續(xù)的，為此給出下列定理［9］：

定理3.1 設(shè)u，ˉu∈L∞（［0，T］；L1（R）∩L∞（R））是方程（1.1）的弱熵解，對應(yīng)初值u0，ˉu0∈L1（R）∩L∞（R），則?t∈［0，T］，

其中C與φ，‖u0‖L∞，‖ˉu0‖L∞有關(guān).

證明 由前面知u，ˉu可看做是其粘性逼近方程（2.1）的解uμ，ˉuμ的極限，關(guān)于（uμ－ˉuμ）方程（2.1）兩端同乘以檢驗(yàn)函數(shù)φ，則

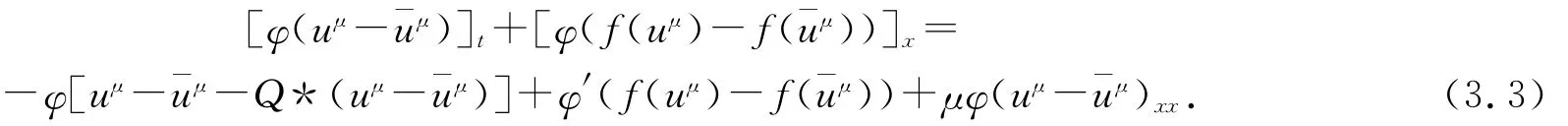
類似于定理2.1的證明，在（3.3）式兩端同乘以ηε（uμ－ˉuμ），其中ηε（ξ）是｜ξ｜的一個(gè)正則逼近，從而得到

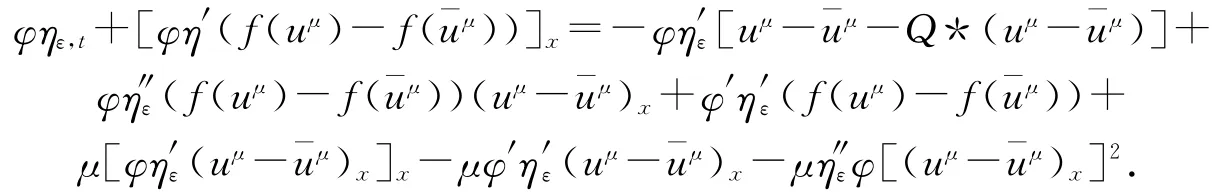
當(dāng)ε→0，對x和t進(jìn)行積分，得到

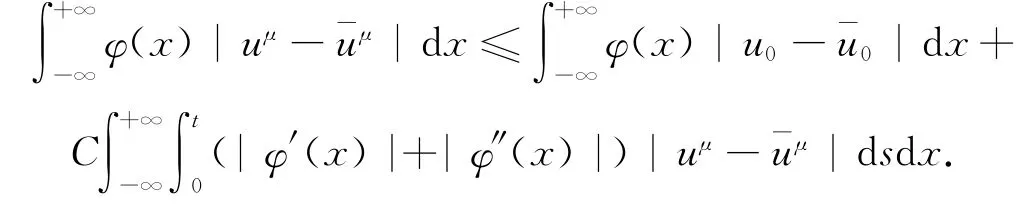
因?yàn)椋ǎ铡洌▁）｜＋｜φ″（x）｜）≤C1φ，且由（3.1）式，并應(yīng)用Gronwall引理，當(dāng)u↓0時(shí)，可以得到（3.2）式.證畢.

在此性質(zhì)下對于初值u0∈L∞（R）在（3.1）式所定義的范數(shù)同樣有類似定理2.1的結(jié)果.

定理3.2 設(shè)u，ˉu∈L∞（［0，T］；L1（R）∩L∞（R））是方程（1.1）的弱熵解，對應(yīng)初值u0，ˉu0∈L∞（R），則?t∈［0，T］有

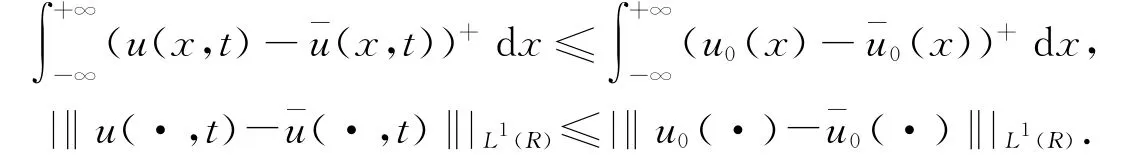
若u0（x）≤ˉu0（x），則

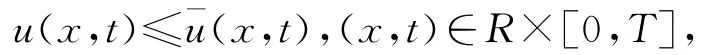
且u，ˉu∈［－a，a］，其中a＝max｛‖u0‖L∞（R），‖ˉu0‖L∞（R）｝.

4 系統(tǒng)的松弛極限

利用伸縮技術(shù)

可以把系統(tǒng)

轉(zhuǎn)化為

當(dāng)ε→0時(shí)，由方程組（4.1）的第二個(gè)方程知，q＝0時(shí)，（4.1）式可以寫為

其中f（u）是屬于C2的光滑函數(shù)，且f（0）＝0.

這樣系統(tǒng)的極限方程變?yōu)橐粋€(gè)雙曲守恒律方程式.為了對這一極限過程進(jìn)行嚴(yán)格的證明，首先對（4.1）式進(jìn)行改寫（類似于預(yù)備知識中的變換），得到

對（4.3）式有一系列定理和推論［8］.

定理4.1 設(shè)u，ˉu∈L∞（［0，T］；L1（R）∩L∞（R））是方程（4.3）的弱熵解，對應(yīng)初值u0，ˉu0∈L1（R）∩L∞（R），則?t∈［0，T］，有

若u0（x）≤ˉu0（x），則

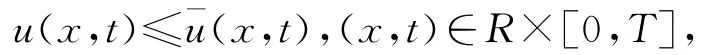
且

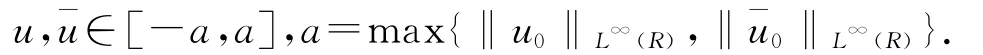
引理4.1 設(shè)uε∈L∞（［0，T］；L1（R）∩L∞（R））是方程（4.3）的弱熵解，對應(yīng)初值u0∈L1（R）∩L∞（R），且

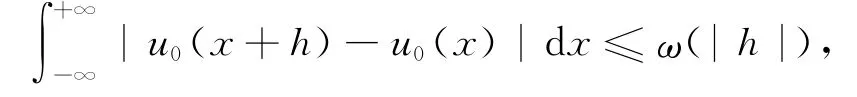
?h∈R，其中ω（r）→0，r→0，r∈［0，＋∞）.那么，?C依賴于‖u0‖L∞（R），使得?t＞0，

由引理4.1的結(jié)果知，uε在L∞上一致有界，且在L1Loc是緊的.由此，有下列雙曲－雙曲型松弛定理：

定理4.2 設(shè)uε∈L∞（［0，T］；L1（R）∩L∞（R））是方程（4.3）的弱熵解，對應(yīng)初值u0∈L1（R）∩L∞（R），那么當(dāng)ε→0時(shí)，?T＞0，uε→u，在LPLoc（R×［0，T］），P＜＋∞時(shí)強(qiáng)收斂，u∈L∞（［0，T］；L1（R）∩L∞（R）），且u是滿足方程（4.2）的唯一熵解，對應(yīng)的初始條件是u0.

［1］ 江澤堅(jiān)，吳智泉.實(shí)變函數(shù)論［M］.北京：高等教育出版社，1994：157－159.

［2］ KAWASHIMA S，NISHIBATA S.Shock waves for a model system of a radiating gas［J］.SIAM J Math Anal，1999，17：95－117.

［3］ KAWASHIMA S，NISHIBATA SHOCK S.Cauchy problem for a model system of the radiating gas：weak solutions with a jump and classical solutions［J］.Math Models Methods Appl Sci，1999，62：69－91.

［4］ 楊麗.一類雙曲與橢圓耦合系統(tǒng)的適定性和松弛極限［D］.長春：東北師范大學(xué)數(shù)學(xué)與統(tǒng)計(jì)學(xué)院，2006.

［5］ 楊麗，張毅.一類粘性逼近方程局部解的存在性［J］.臨沂師范學(xué)院學(xué)報(bào)，2008，30（3）：19－22.

［6］ KAWASHIMA S.Larger－time behavior of solution stohyperbolic－parabolic system of conservation laws and applications［J］.Proceeding of the Royalsociety of Edinburgh，1987，106（A）：169－199.

［7］ HAMER K.Nonlinear effects on the propagation of sounds waves in a radiating gas［J］.Quarter Journ Mech Appl Math，1971，24：155－168

［8］ KAWASHIMA S，NISHIBATA S.Weak solutions withashockto amodelsystem ofthe radiating gas［J］.Sci Bull Josai Univ，1998，5：119－130.

［9］ NISHIBATA S.Asymptotic behavior of solution stoamodel system of radiating gas with discontinuous initial data［J］.Math Models Methods Appl Sci，2000，10：1209－1231.

The well－posedness extend of a model for radiating gas's solution

YANG Li
（College of Public Health，Weifang Medical University，Weifang 261053，China）

In this paper，the initial condition is considered for a class of hyperbolic and elliptic coupled system well posedness of the solution，and the solution space is extended in the semigroup sense，make the system well posedness of the meaning and nature of the new.At the same time，the well posedness of the solution of this system，the use of hyperbolic type expansion technology，discuss the relaxation limit of the system.

scalar conservation laws；well－posedness；semigroup；relaxation limit

O 175 ［學(xué)科代碼］ 110·47

A

（責(zé)任編輯：陶 理）

1000－1832（2014）02－0012－04

10.11672／dbsdzk2014－02－003

2013－03－31

數(shù)學(xué)天元基金資助項(xiàng)目（NSFC－11126269）.

楊麗（1979－），女，碩士，講師，主要從事偏微分方程研究.