回歸課本 注重課本原題在高考題中的應用
——余弦定理的又一妙用

宋顯梅

（福建省廈門康橋中學，福建 廈門 361000）

回歸課本 注重課本原題在高考題中的應用
——余弦定理的又一妙用

宋顯梅

（福建省廈門康橋中學，福建 廈門 361000）

余弦定理反映了三角形的一種邊角關系，將其轉化為單純的角的關系，對解決一些三角恒等變形問題會起到一種獨特的效果。

高考；轉化；余弦定理；應用

一、問題的提出

2012年福建省理科高考第17題是本份試卷的一個亮點。一方面它以研究性學習為背景，考查學生運算求解能力、抽象概括能力、推理論證能力，考查特殊與一般思想、化歸與轉化思想，充分體現了高中新課程的理念；另一方面本題位于試卷的第17題，充分體現出命題組不為難學生和送分的意圖，但許多平時水平較高的考生表現并不理想，體現在運算量和時間成本投入較大。2012年福建省狀元（有四位學生并列）的數學分數也只在136～139分之間，沒有突破140分，這和前面用時較多不無關系，也就說明了這個問題。最后從落腳到探究課本的定理和例題這一視角看，給出的評分標準和標準答案也不是最佳。

【2012年福建省理科高考第17題】回放：

某同學在一次研究性學習中發現，以下五個式子的值都等于同一個常數：

（Ⅰ）試從上述五個式子中選擇一個，求出這個常數；

（Ⅱ）根據（Ⅰ）的計算結果，將該同學的發現推廣為三角恒等式，并證明你的結論。

（本題的解答見后，需要說明的是該解答屬筆者原創。）

二、問題的解決

我們來看下一組題目。求下列三角函數的值：

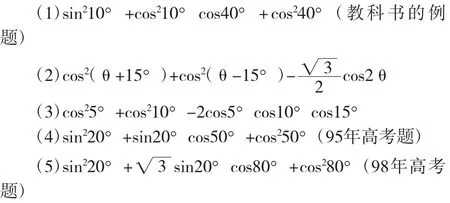
其實它們原于教科書的例題：sin210°+sin10°cos40° +cos240°課本的解法如下：

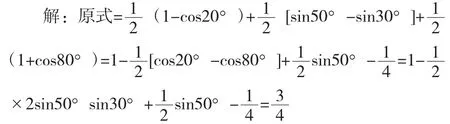
【點評】此解法的利弊很明顯，利：比較全面地復習了三角中比較常用的倍半公式、降次公式等公式；弊：運算量較大和加大了時間成本，這將導致運算出現誤差和影響后面區分度較大的考題的解答。在當今120分鐘要完成22道題（每題約5分鐘）的高考中如何縮短時間提高效率顯得重要。怎么辦？

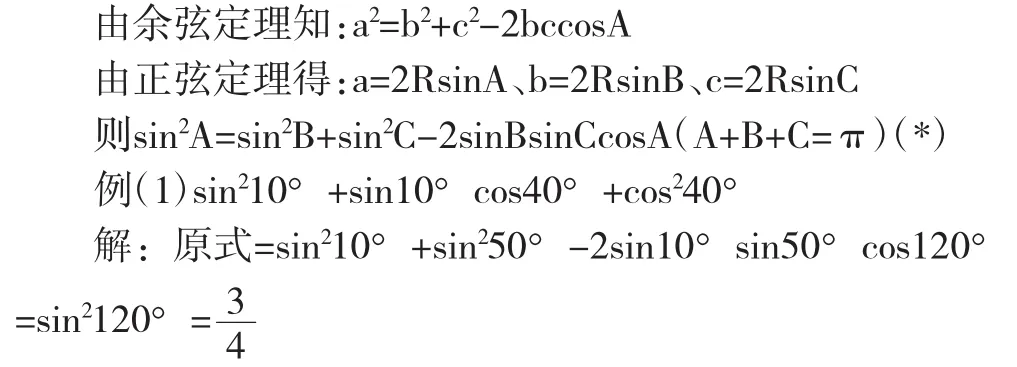
【點評】整個解答運算量小、準確率高、時間成本有效控制，一氣呵成、干凈利落。

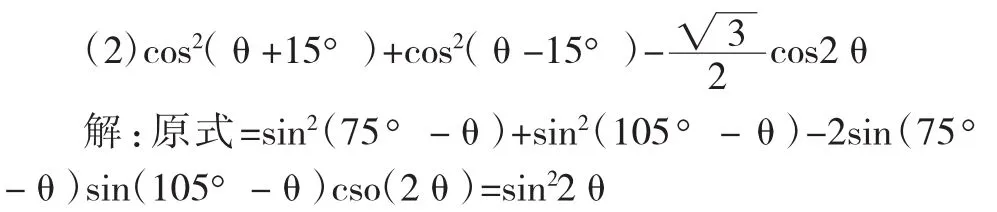
【點評】對類似該組題型的選擇和填空題我們利用（*）式可直接得出結果。對該形式的解答題可利用它檢查結論：或對（*）式加以證明后（易證）再加以應用。效果比較明顯。

三、運用上述推廣（＊）對2012年福建省理科高考第17題的原創解答

（Ⅰ）選擇（1）式，計算如下：

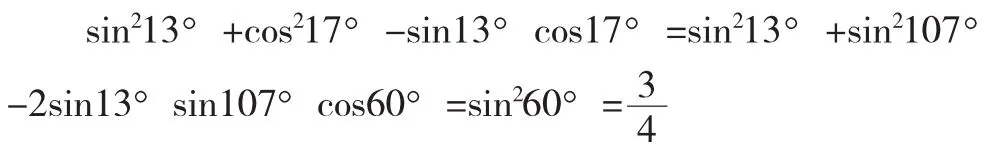
（Ⅱ）三角恒等式為sin2α+cos2（30°-α）-sinαcos（30°-α）=

【高考評分標準如下】：

（Ⅱ）三角恒等式為sin2α+cos2（30°-α）-sinαcos（30°-α）=

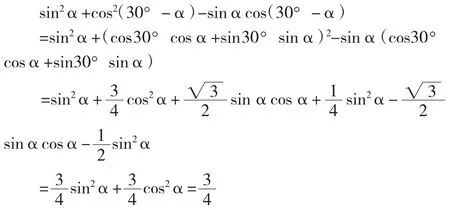
解法二：（Ⅰ）同解法一

（Ⅱ）證明如下：

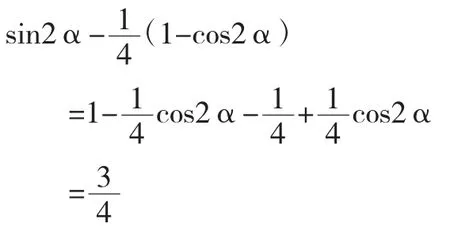
【對比說明】限于文章的篇幅對高考標準答案不再進一步評價。本題原創解法的可取之處在于敏銳地捕捉出它原于教科書的例題，固本朔源，探究余弦定理的等價變形，本題完美解出一舉成功拿下，所用時間可以接受。事半功倍。只要我們真正意義上地培養學生創新精神，我們的高三數學迎考將更加有效。

四、結論的推廣與證明

下面給出已知：A+B+C=π時sin2A=sin2B+sin2C-2sinB-sinCcosA（*）的推廣：

【結束語】

隨著高考制度的改革，高考中三角的試題大多來源于課本中的習題和例題或它們的變形，因此復習時應“立足于課本，著眼于提高”，注重等價轉化在教學中的應用，在教學中，我們應努力使學生熟練掌握公式的正用、反用、變形用或在特定條件下使用，即注重等價轉化在教學中的應用，因為它可以提高思維起點，縮短思維線路，從而使運算流暢自然，縮短時間提高效率。

G633.6

A

1674-9324（2014）07-0231-02