改進的TRUST方法在航磁數據線性特征增強中的應用

耿美霞，黃大年，楊慶節

吉林大學地球探測科學與技術學院，長春 130026

改進的TRUST方法在航磁數據線性特征增強中的應用

耿美霞，黃大年，楊慶節

吉林大學地球探測科學與技術學院，長春 130026

基于各向異性擴散濾波的TRUST方法對航磁數據線性特征趨勢增強時，未考慮數據光滑區域與異常邊緣區域的區別，在光滑區域擴散持續進行，導致光滑區域產生許多虛假小異常。為此，提出一種改進的TRUST方法。該方法對TRUST方法中擴散張量的特征值通過引入相干性的辦法進行了重新構造，使其能夠正確識別光滑區域和異常邊緣區域，并自動降低光滑區域的擴散速率，從而避免濾波過程中虛假異常的產生。在模型試驗中，將該方法與TRUST方法處理結果進行了對比。結果顯示，采用改進后的TRUST方法，不僅使航磁數據圖上“串珠狀”走樣現象被消除，而且光滑區域的低振幅信息也被很好地保存。最后應用此方法對某地區的航磁數據進行趨勢增強濾波，證實了該方法的實用性。

航磁數據；串珠狀走樣；趨勢增強；TRUST方法

0 引言

地球物理數據處理往往要求數據是間隔均勻的網格數據，因此需要采用合理的網格化插值方法對原始測量數據進行網格化[1]。網格數據的質量直接影響后期數據處理以及解釋圖件的質量和可靠性。然而在航空數據采集中，測線之間的距離往往比測點之間的距離大很多，使得測量數據的不均勻性非常嚴重。這種密度顯著不均勻的數據被稱為測線型數據，對測線型數據網格化，常常會帶來假異常[1]。例如，當線性異常的趨勢方向與測線方向的夾角為銳角時，網格化后會出現“串珠狀”假異常，并且夾角越小，這種假異常現象越明顯。“串珠狀”假異常不僅降低了航磁數據圖形光滑度，還使本應明顯的線性異常特征變成了小異常體特征，給后續處理和解釋工作帶來不便，甚至導致錯誤的解釋。因此，為了滿足當前高精度航空物探數據處理和解釋的需要，保持原始測量信息的同時需要消除或減弱“串珠狀”假異常現象，這已成為一個不能回避的問題。

大量研究[2-5]表明，無論是采用最小曲率、Akima插值還是雙三次樣條插值等方法，都會產生“串珠狀”假異常現象，即“串珠狀”假異常與常規網格化方法無關，而是由于測線間采樣不足導致的短波長特征空間混疊效應而產生的。往往當測線間距大于或等于異常寬度的一半時，就會出現這種現象，并且異常走向與測線夾角越小，“串珠狀”假異常越明顯。前人研究[6-9]表明，使用最小曲率網格化過程中，用實際測量梯度數據代替計算得到的梯度數據，在一定程度上能夠增強航磁數據中的線性特征，提高異常分辨率。但由于測量設備的限制，梯度數據并非總能獲得。

由于“串珠狀”走樣問題的廣泛存在，已經有很多學者對此進行了研究。Zhou[10]使用Radon變換的方法進行趨勢增強，但是該方法只能對一個方向進行趨勢增強。Sykes等[11]采用2-D Radon變換，通過在變換域中取閥值，對大于閥值的變換值作一定的增長，這樣反演重建后的圖像中相應的線性特征得到增強。但由于重磁圖像線性特征的灰度相比于“背景”值并無特殊之處，閥值的選取較為困難。另外，該方法不能準確恢復原始圖像的振幅，限制了其在高精度航磁數據處理中的應用。Hansen[12]采用各向異性克里金方法對數據進行網格化，由于該方法只能對一個固定的方向進行趨勢增強，尚無法在有多個方向的趨勢數據中應用。Fitzgerald等[13]沿著異常值方差最小的方向，從測線上抽取數據值，并將這些抽取的數據作為原始觀測數據插入到測線之間，隨后進行樣條或最小曲率網格化；該方法需要確定一個接受度來判定特征是否為異常，網格化結果受接受度的影響非常大，并且對于走向與測線夾角小于45°的異常，處理效果不是很好。此外，Keating[14]采用最鄰近分析法找出測線上的最大值和最小值，通過連接相鄰測線上最鄰近的最大值(或最小值)來確定插入測線間的數據，然后再進行網格化；該方法在線性特征走向與測線夾角比較大時能取得不錯的趨勢增強效果，但在構造復雜地區容易產生錯誤的線性趨勢。

此外，基于偏微分方程尤其是各向異性擴散濾波方程的方法也已被應用到航磁數據趨勢增強領域中[1, 15-16]。Smith等[16]成功地將各向異性擴散濾波方法應用到航磁數據趨勢增強領域。該方法被稱為TRUST(trends using structure)方法，它是在網格化后的數據上進行的，能自動對多個走向的趨勢特征進行增強。然而TRUST方法未考慮數據光滑區域與異常邊緣區域的區別，擴散在光滑區域持續進行，因而在光滑區域不可避免地產生虛假小異常。這種假異常在解析信號模圖上會更加明顯[16]，需要后續處理來消除。

筆者針對TRUST方法進行趨勢增強時在光滑區域中產生虛假異常的缺點，基于相干性[17]重新構造新的特征值，從而構造新的擴散張量。新的特征值能夠正確判斷航磁異常數據中的光滑區域和異常邊緣區域，以實現對不同的異常特征進行不同程度的擴散濾波，從而在消除“串珠狀”構造的同時保護光滑區域的低振幅信息。

1 基于各向異性擴散濾波的TRUST趨勢增強方法

基于偏微分方程的擴散濾波理論最初由Perona等[18]提出，并在數字圖像處理領域中得到廣泛應用。其構建的非線性擴散濾波模型為

其中：t為擴散時間；div為散度算子；g(·)為擴散濾波器的擴散系數，為一非負單調遞減函數，且滿足g(0)=1，g(∞)=1；u為t時刻的擴散濾波結果；u0表示t=0時的原始數據，作為該擴散方程的初始條件。

為了滿足增強圖像中各向異性紋理結構的需要，Weickert[19]通過對圖像數據中各向異性結構的分析，將式(1)中的擴散系數變為張量，并構建了如下的張量型擴散模型[15]：

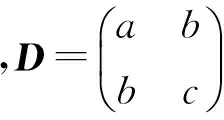
J0(uσ)=uσuσT=

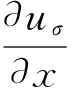
Jρ(uσ)=Gρ*(uσ

第一個特征向量v1=(cosφ,sinφ)T滿足

‖

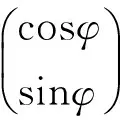
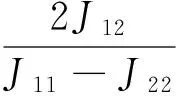
各向異性擴散張量D與結構張量J的特征向量相同，在Smith等[16]提出的TRUST方法中，其特征值為

式中，λ1和λ2又被稱為擴散速率。D的分量分別為

在實際應用中，式(2)可以用有限差分方法求解，空間導數通常由中心差分代替[15]。式(2)的有限差分形式為

un+1=un+Δtdiv(Dn

其中：Δt為空間步長，通常情況下，只要Δt<0.25，式(11)在一定迭代次數內就是穩定的；un是u(x,y)在位置(x,y)處nΔt時刻的近似。由于擴散張量D在每次迭代過程中變化非常小，因此筆者選擇在經過一定迭代次數后再重新計算一次D，這樣可以大大提高該方法的計算效率。

2 改進的TRUST方法

觀察式(9)可發現，特征值λ2沒有考慮到光滑區域與邊緣區域之間的差別，在相對光滑的區域濾波容易導致虛假異常的產生：在光滑區域，只要存在梯度各向異性，就會沿著梯度值較小的方向擴散，從而導致虛假異常的出現。

實際上，結構張量的特征值μ1和μ2包含了圖像結構信息[17]。所以特征值μ1、μ2可以用來描述圖像的局部結構特征：在光滑區域μ1≈μ2≈0；對于構造的邊緣區域μ1?μ2≈0；在拐角的邊界區域有μ1>μ2?0。由此定義相干性H[17]如下：

根據局部圖像的相干性，筆者構造了新的特征值：

其中，C為常數。

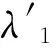
擴散濾波的過程是將原始的圖像數據，即航磁數據進行濾波。其在消除“串珠狀”假異常的同時，不可避免地造成原始測點上數據的改動。這樣的濾波處理違背了高精度航磁異常處理的原則[16]。一個防止原始測線數據被改動的簡單方法，就是在迭代濾波過程中將這些測點數據固定不變。在實際應用中，另一個問題是迭代停止時間的選擇。迭代次數過少，圖像上的線性特征得不到足夠的增強；而迭代次數過多不僅花費的計算時間較長，還會導致圖像被過度平滑。因此，選擇適當的迭代次數對最終趨勢增強效果非常重要。根據筆者的試驗結果，一般情況下，迭代次數取300～500，就能得到比較滿意的趨勢增強效果。

3 關于幾個參數的意義和選擇

在結構張量構造中有2個參數，σ和ρ。其中，參數σ被稱為噪聲尺度[16]。對原始數據處理前，先用噪聲尺度為σ的高斯核對數據進行卷積，可以保證在進行求導計算時，尺度小于σ的數據不對導數計算產生影響，從而保證了求導過程的穩定性和可靠性。在選取參數σ時，根據航磁數據的噪聲水平進行選擇，才能達到預期的目的。根據筆者的試驗結果，發現通常σ選擇為1倍測線距左右時，能夠得到較好的濾波效果。

參數ρ被稱為綜合尺度，它反映的是圖像的紋理特征[16]。它的作用是對結構張量的方向進行濾波，進一步消除尺度規格小于ρ的噪聲干擾。如果ρ的值過大，就會使濾波后的數據過度平滑，丟失原有信息。根據筆者的試驗結果，通常ρ選擇為1.5倍的測線距。這樣能夠保證連續出現在相鄰2條測線上的“串珠”異常得到增強。

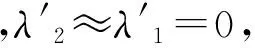
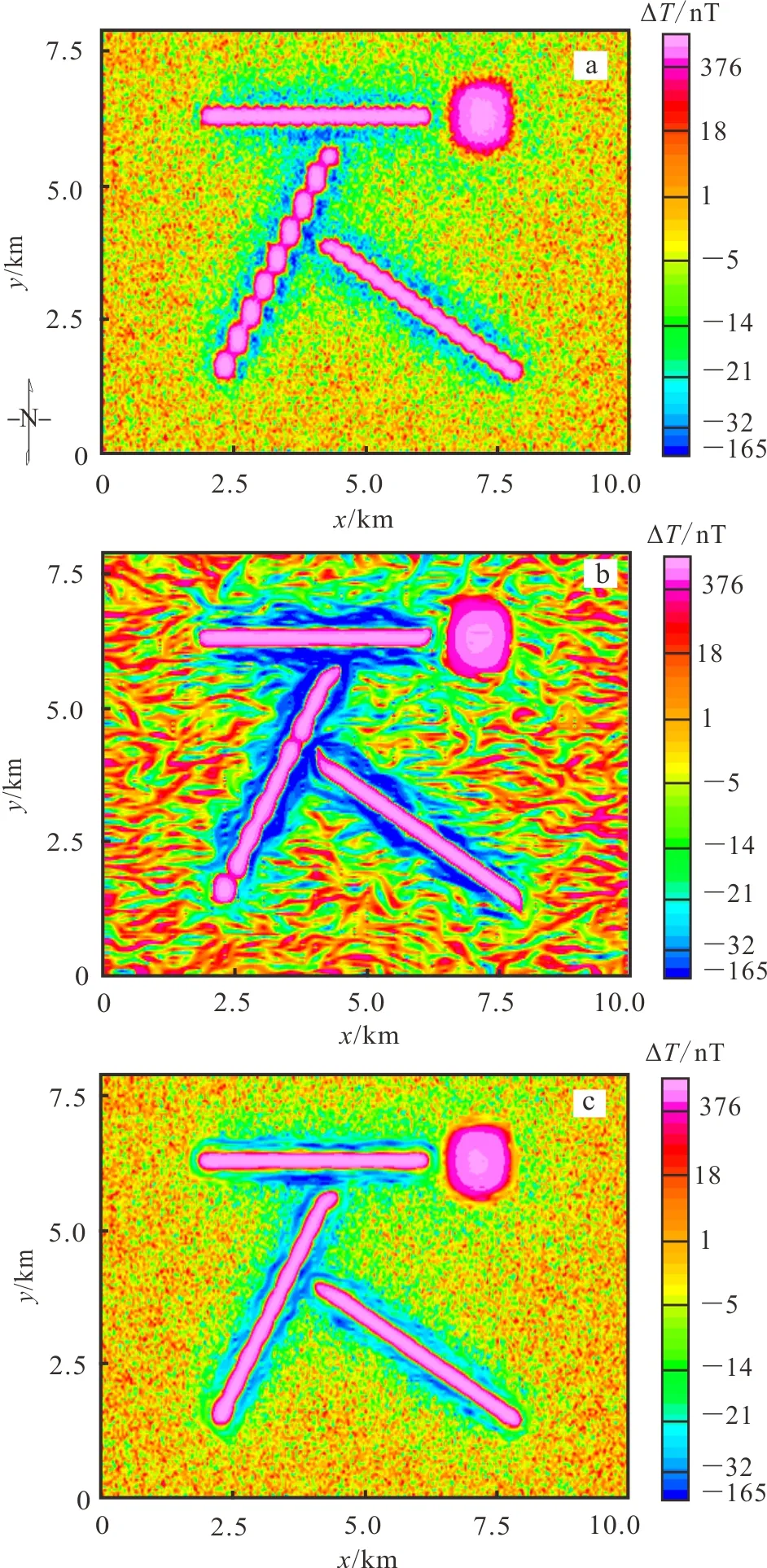
a.濾波前；b.TRUST方法濾波后；c.改進的TRUST方法濾波后。圖1 趨勢增強前后航磁異常(ΔT)圖Fig.1 Application of the trend enhancement filter to the aeromagnetic data

4 模型計算與對比

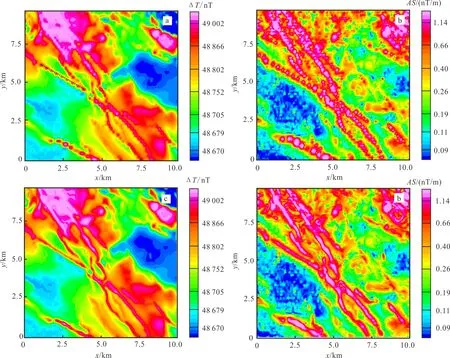
a.原始航測數據網格化后異常；b.原始異常解析信號模；c.經過改進的TRUST方法濾波后的航磁異常；d.經過改進的TRUST方法濾波后異常的解析信號模。AS=。圖2 航測數據趨勢增強前后異常和相應的解析信號模圖Fig.2 Comparison of the original aeromagnetic data and the data after trend enhancement as well as the corresponding analytic signal maps

為了驗證改進的TRUST方法消除“串珠狀”假異常的有效性，筆者采用了含有高斯白噪聲的組合磁性體模型對趨勢增強效果進行檢驗。組合模型包括1個塊狀和3個不同走向的脈狀體，磁化方向I0=75°，磁偏角A0=25°，磁化強度J=1 A/m。測線方向為南北方向。如圖1a所示，3個脈狀體與測線的夾角分別為30°，60°和90°。測線間距為 200 m，測線上測點間距為 10 m，在原始的測線數據中加入了8%的高斯白噪聲。采用最小曲率方法對測線數據進行網格化，網格間距為 50 m。圖1a 給出了網格化后的航磁異常。從圖1a 可以看到：當線性磁異常與測線夾角為銳角時，網格化后異常呈現出“串珠狀”假異常特征，并且，夾角越小，這種走樣現象越嚴重；垂直于測線的線性磁異常以及塊狀磁異常，雖然沒有出現走樣現象，但是網格化后異常的邊緣呈“鋸齒狀”，影響了圖像的光滑性。

圖1b顯示的是經過TRUST方法擴散濾波后的航磁異常圖。迭代次數為300。可以看到：經過TRUST方法濾波后，與測線夾角為銳角的線性趨勢特征得到增強，“串珠狀”假異常基本被消除；同時，塊狀異常和與測線垂直的線性異常邊緣的“鋸齒”特征也被消除。然而，由于噪聲的存在，濾波后光滑區域產生了大量小的假異常。此外沿測線方向也有少量的高頻假異常產生。

圖1c顯示的是經過改進的TRUST方法擴散濾波后的航磁異常。迭代次數同樣為300。可以看到：經過改進的TRUST方法濾波后，與測線夾角為銳角的線性趨勢特征得到增強，“串珠狀”假異常被完全消除；塊狀異常和與測線垂直的線性異常邊緣的“鋸齒”特征也被很好地消除。此外，由于改進的TRUST方法中擴散張量的特征值能夠在相對平滑區域自動降低擴散速率，有效地保護了原始低振幅信息，從而避免了平滑區虛假小異常的產生。

5 實例分析

圖2a 為某地區采集的航空磁異常數據，該地區存在大量的西北--東南走向的脈狀磁性體。飛行測線距為 200 m，測點距為 17 m，測線方向為東西方向。采用最小曲率法對原始的航磁數據進行網格化，網格間距為 40 m。可以看到，圖2a上存在明顯的“串珠狀”走樣，并且與測線方向夾角越小，“串珠狀”走樣越明顯。圖2b 為該異常的解析信號模。解析信號模類似于航磁化極圖，能夠部分消除斜磁化影響，異常幅度大體反映了場源的相對磁性強度[20]，并且對異常體的邊緣非常敏感，因此常被用來估計磁異常體的水平位置。在解析信號模(圖2b)上，“串珠狀”走樣特征更加明顯，給后續處理和解釋工作帶來不便，甚至可能導致錯誤的解釋。

圖2c 為圖2a 中的數據經過改進后的TRUST方法濾波后的航磁異常圖。迭代次數為300。可以看到，經過濾波之后，“串珠狀”假異常被消除，同時線性特征也得到了增強。由于改進后的TRUST方法能夠在光滑區域自動降低擴散速率，因此光滑區域的低振幅信息也被很好地保存下來。圖2d 為圖2c 的解析信號模，可以看到，“串珠狀”走樣特征也已被消除，使后期解釋更加方便。

為了檢驗趨勢增強前后航磁圖上數據的變化，從圖2a 上用沿某一線性趨勢方向虛線標出的點提取數值，并將抽取的數據點構成一條剖面(圖3)。經過300次迭代濾波后，該剖面數據再次顯示在圖3中。可以看到，濾波后剖面數據上的波峰抖動被消除，得到了一個相對光滑的長波長曲線。圖3中五角星指示的峰值都是航空測線穿越的位置。由于在進行濾波運算的同時固定原始測點數據不變，所以濾波后原始測點上的數據被保存下來。

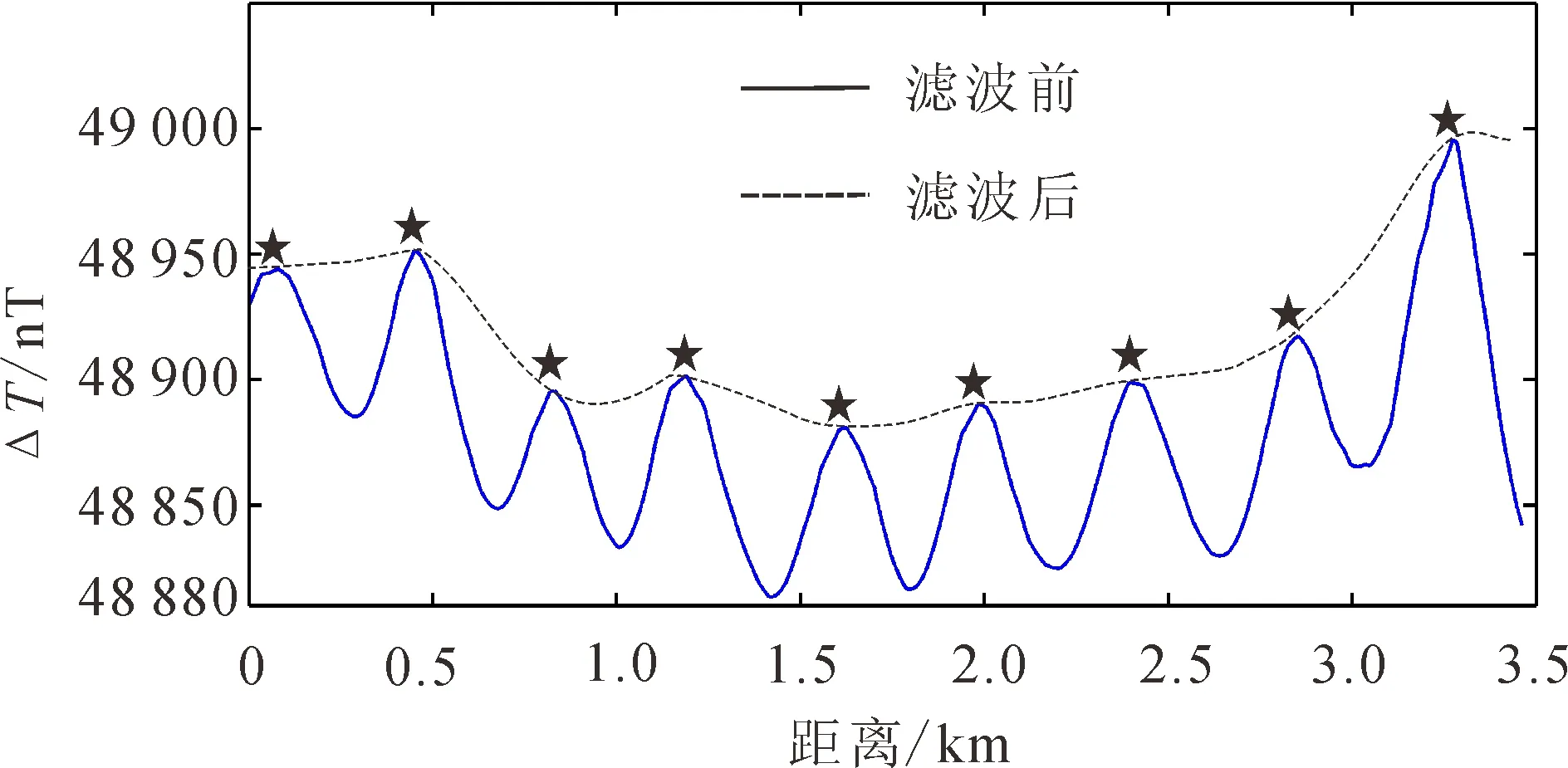
圖3 濾波前后抽取的剖面數據對比Fig.3 Comparison of the original data on the ridge profile and the data after trend enhance

6 結束語

本文針對TRUST方法擴散張量特征值的選取不適合光滑區域濾波而導致虛假異常的缺點，引入圖像相干性，重新構造了擴散張量的特征值。新的特征值能夠正確區分航磁異常中的異常邊緣和光滑區域，并在光滑區域自動降低擴散速率以便有效地保護低振幅信息，從而避免了假異常的產生。此外，為了保護原始測信息，本文算法在濾波過程中對原始測線上的數據點進行了約束保護，使得處理后的數據精度得到很大提高，在實際數據應用中取得了非常好的效果。

[1] 姚長利，龐旭林. 航磁數據線性特征增強濾波方法技術研究[C]//中國地球物理年會.北京：中國地球物理學會，2009：267. Yao Changli, Pang Xulin. Researeh on the Enhancement Trends of Magnetic Date[C]// Chinese Geophysics Society Annual Meeting. Beijing: Chinese Geophysical Society，2009: 267.

[2] Billings S, Richards D. Quality Control of Gridded Aeromagnetic Data[J]. Exploration Geophysics, 2000, 31 (4): 611-616.

[3] 李麗麗，杜曉娟，馬國慶. 改進的局部波數法及其在磁場數據解釋中的應用[J]. 吉林大學學報：地球科學版，2012，42(4): 1179-1185. Li Lili, Du Xiaojuan, Ma Guoqing. Improved Local Wave Number Methods in Interpretation of Magnetic Fields[J]. Journal of Jilin University: Earth Science Edition, 2012, 42(4): 1179-1185.

[4] 曾昭發，吳燕岡，郝立波，等. 基于泊松定理的重磁異常分析方法及應用[J]. 吉林大學學報：地球科學版，2006，36(2)： 279-283. Zeng Zhaofa, Wu Yangang, Hao Libo, et al. The Poisson’s Theorem Based Analysis Method and Application of Magnetic and Gravity Anomalies[J]. Journal of Jilin University: Earth Science Edition, 2006, 36(2): 279-283.

[5] 方東紅，曾昭發，陳家林. 基于小波分析的重磁數據求導方法及應用[J]. 吉林大學學報：地球科學版，2008，38(6)：1049-1054. Fang Donghong, Zeng Zhaofa, Chen Jialin. The Derivatives Calculation Based on Wavelet Analysis of G/M Data and Its Application[J]. Journal of Jilin University: Earth Science Edition, 2008, 38(6): 1049-1054.

[6] Marcotte D L, Hardwick C D, Lemieux J M, et al. Aeromagnetic Gradiometry Methods: A Study Using Real Data[C]//60th Annual International Meeting. SEG: [s.n.], 1990:584-586.

[7] Cowan D R, Baigent M, Cowan S. Aeromagnetic Gradiometers: A Perspective[J]. Exploration Geophysics, 1995, 26: 241-246.

[8] McMullan S R, McLellan W H, Koosimile D I. Three Dimensional Aeromagnetics[J]. Preview, 1995, 57: 83-91.

[9] Hardwick C. Gradient-Enhanced Total Feld Gridding[C]// 69th Annual International Meeting.SEG: [s.n.], 1999:381-384.

[10] Zhou Y X. Radon Transform Application to the Im-proved Dridding of Airborne Geophysical Survey Data[J]. Geophysical Prospecting, 1993, 41: 459-494.

[11] Sykes M P, Das U C. Directional Filtering for Linear Feature Enhancement in Geophysical Maps[J]. Geophysics, 2000, 65: 1758-1768.

[12] Hansen R O. Interpretive Gridding by Anisotropic Kriging[J]. Geophysics, 1993, 58: 1491-1497.

[13] Fitzgerald D, Yassi N, Dart P. A Case Study on Geophysical Gridding Techniques: Intrepid Perspective[J]. Exploration Geophysics, 1997, 28: 204-208.

[14] Keating P. Automated Trend Reinforcement of Aero-magnetic Data[J]. Geophysical Prospecting, 1997, 45: 521-534.

[15] 孫夕平，杜世通，湯磊. 相干增強各向異性擴散濾波技術[J].石油地球物理勘探，2004，39(6)：651-655. Sun Xiping, Du Shitong, Tang Lei. Coherent-Enhancing Anisotropic Diffusion Filtering Technique[J]. Oil Geophysical Prospecting, 2004, 39(6): 651-655.

[16] Smith R S, O’Connell M D. Interpolation and Grid-ding of Aliased Geophysical Data Using Constrained Anisotropic Diffusion to Enhance Trends[J]. Geophysics, 2005, 70(5): 121-127.

[17] 王大凱，侯榆青，彭進業. 圖像處理的偏微分方程方法[M]. 北京：科學出版社，2008. Wang Dakai, Hou Yuqing, Peng Jinye. Partial Differential Equation in Image Processing[M]. Beijing: Science Press, 2008.

[18] Perona P, Malik J. Scale Space and Edge Detection Using Anisotropic Diffusion[J]. IEEE Trans Pattern Anal Mach Intell, 1990, 12: 629-639.

[19] Weickert J. Anisotropic Diffusion in Image Pro-cessing[M]. Stuttgart: Teubner,1998.

[20] 駱遙，王明，羅鋒，等. 重磁場二維希爾伯特變換：直接解析信號解釋方法[J]. 地球物理學報，2011，54(7)：1912-1920. Luo Yao, Wang Ming, Luo Feng，et al. Direct Analytic Signal Interpretation of Potential Field Data Using 2-D Hilbert Transform[J]. Chinese Journal of Geophysics, 2011, 54(7): 1912-1920.

Application of Improved TRUST Method in Enhancing Linear Trends of Aeromagnetic Data

Geng Meixia，Huang Danian，Yang Qingjie

College of GeoExploration Science and Technology, Jilin University, Changchun 130026, China

As for the enhancement of linear Trends, the TRUST method proposed by Smith and O’Connell does not consider the distinctions between the smooth area and other image features. The diffusion is carried on in smooth area and thus inevitably produces artifacts. An improved TRUST method was proposed. The eigenvalues of the structure matrix are reconstructed，so that the method only diffuses the image in specific areas where strong anisotropy is detected. This method is tested on both synthetic and field data sets. The results indicate that the method can be used efficiently to enhance linear structure locally in multiple directions. We have also compared the proposed method with the TRUST method by applying them to the synthetic data set. The results demonstrate that the proposed method can produce better effect with fewer artifacts.

aeromagnetic data；boudinage；enhancement of trends；TRUST method

2014-03-04

國家“863”計劃項目(2014AA06A613)；吉林大學研究生創新基金資助項目(2014066)

耿美霞(1986--)，女，博士研究生，主要從事航空重磁數據處理和反演方面的研究，E-mail:gengmeixia@126.com

黃大年(1958--)，男，教授，博士生導師，國家千人計劃特聘專家，主要從事移動平臺探測數據處理與解釋及一體化軟件平臺開發，E-mail:dnhuang@jlu.edu.cn。

10.13278/j.cnki.jjuese.201404301.

10.13278/j.cnki.jjuese.201404301

P631.2

A

耿美霞，黃大年，楊慶節.改進的TRUST方法在航磁數據線性特征增強中的應用.吉林大學學報:地球科學版,2014,44(4):1333-1339.

Geng Meixia，Huang Danian，Yang Qingjie.Application of Improved TRUST Method in Enhancing Linear Trends of Aeromagnetic Data.Journal of Jilin University:Earth Science Edition,2014,44(4):1333-1339.doi:10.13278/j.cnki.jjuese.201404301.