基于相對高程異常的GPS高程擬合方法探討

陳艷紅，馬全明，劉瑞敏，毛曉康

(1.石家莊經(jīng)濟學(xué)院，河北 石家莊 050031；2.北京城建勘測設(shè)計研究院有限責(zé)任公司，北京 100101；3.中南大學(xué)，湖南 長沙 410083)

基于相對高程異常的GPS高程擬合方法探討

陳艷紅1，馬全明2，劉瑞敏2，毛曉康3

(1.石家莊經(jīng)濟學(xué)院，河北 石家莊 050031；2.北京城建勘測設(shè)計研究院有限責(zé)任公司，北京 100101；3.中南大學(xué)，湖南 長沙 410083)

在傳統(tǒng)二次曲面GPS高程擬合的基礎(chǔ)上，提出一種基于相對高程異常的GPS高程擬合方法。該方法首先通過相對正常高高程異常值的改正，把GPS點的相對大地高轉(zhuǎn)化為相對正常高，然后將相對正常高與已知點的正常高高程連算，按照傳統(tǒng)的水準(zhǔn)測量計算方法平差解算，即能得到最優(yōu)解的正常高。采用某山區(qū)工程實例數(shù)據(jù)進行了驗證，表明該方法在地勢起伏較大的測區(qū)比二次曲面擬合得到的精度要高。

大地高；正常高；GPS高程擬合；高程異常

一、引 言

近年來，GPS衛(wèi)星定位技術(shù)已在測繪領(lǐng)域得到廣泛應(yīng)用，它不僅能獲取高精度的平面位置，而且能獲得高精度的大地高，如果將大地高轉(zhuǎn)換為我國采用的正常高，代替部分的傳統(tǒng)水準(zhǔn)作業(yè)，具有較大的經(jīng)濟效益[1]。

目前，對GPS高程數(shù)據(jù)進行轉(zhuǎn)換的常用方法有物理重力法和幾何解析法兩種。在實際工程應(yīng)用中，由于無法獲得必要的重力數(shù)據(jù)，故重力法難以普及[2]。因此，在工程應(yīng)用中以幾何解析法居多，其主要包括解析多項式法、加權(quán)均值法、多面函數(shù)法及近年來非常流行的神經(jīng)網(wǎng)絡(luò)法等[3-10]。這些 GPS高程擬合方法的精度受到聯(lián)測水準(zhǔn)點在測區(qū)的分布情況和數(shù)量的限制，只考慮了高程異常與點的位置間的關(guān)系，而沒有考慮高程異常與點的高程間的關(guān)系。本文在GPS高程擬合時不僅考慮高程異常與位置的關(guān)系，以及與大地高的關(guān)系[11]，并提出了基于相對正常高高程異常的GPS高程擬合模型。

二、基于相對正常高高程異常的GPS高程擬合原理

由于原有GPS高程擬合精度受到聯(lián)測水準(zhǔn)點在測區(qū)的分布情況和數(shù)量的限制，只考慮到高程異常與點的位置有關(guān)，而沒有考慮到高程異常與點的高程的關(guān)系。因此本文在傳統(tǒng)二次曲面GPS高程擬合的基礎(chǔ)上，不僅考慮高程異常與位置的關(guān)系，還考慮與相對大地高的關(guān)系。

原有GPS高程擬合思路是先求出高程異常ζ，然后把大地高轉(zhuǎn)化為正常高。本文在擬合時不求高程異常ζ，而是先把GPS點的相對大地高轉(zhuǎn)化為相對正常高，須加一個改正數(shù)，即相對正常高高程異常值。在得到相對正常高高程后，再與已知點的正常高高程連算，按照傳統(tǒng)的水準(zhǔn)測量計算方法平差解算，就能得到最優(yōu)解的正常高。

1.GPS相對大地高高程轉(zhuǎn)化為相對正常高高程

將GPS大地高程數(shù)據(jù)轉(zhuǎn)化為水準(zhǔn)測量的相對正常高高程Δh0，即

式中，HA、HB分別表示A、B兩點的大地高，大地高即GPS數(shù)據(jù)中的高程數(shù)據(jù)；分別表示A、B兩點的正常高，即我國使用的高程系統(tǒng)；ΔhAB表示A點到B點的相對大地高，即 A、B兩點的大地高差；表示A點到B點的相對正常高高差，即A、B兩點正常高高差；ζAB表示A點到B點的相對正常高高程異常，即A、B兩點的高程異常值的差值。

從式(1)中可以看出，只要得到兩點的相對正常高高程異常ζAB，就可以把GPS大地高程數(shù)據(jù)轉(zhuǎn)化為兩點的相對正常高，再根據(jù)兩點的相對正常高和已知點的正常高進行連算，利用間接平差進行計算，就可以得出測區(qū)所有點的正常高高程，把GPS大地高轉(zhuǎn)化為正常高高程。

2.相對正常高高程異常求解

(1)建立相對正常高高程異常ζij模型

根據(jù)相對正常高高程異常ζij不僅與點的位置有關(guān)系，還與相對大地高有關(guān)，建立如下函數(shù)模型

式中，ζij表示i點到j(luò)點的相對正常高高程異常，ζij＝ζj－ζi；Δhij表示i點到j(luò)點的相對大地高高程，Δhij＝Hj－Hi；(Xj，Yj)表示j點平面坐標(biāo)。

在測區(qū)中選定一個起始點，所有點的相對正常高高程異常都是基于這一個點的。這個起點最好選在測區(qū)的中間。

為了便于擬合計算，對上面的函數(shù)模型具體化，ζij與Δhij、Xj、Yj多項式關(guān)系為

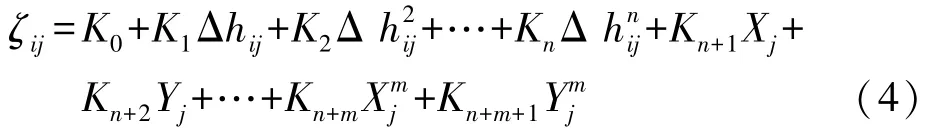
式中，Ki(i＝0，1，…，n＋m＋1)為系數(shù)。

對于不同的測區(qū)，根據(jù)已知數(shù)據(jù)來選擇系數(shù)Ki的個數(shù)。

(2)相對正常高高程異常ζij的求解

利用已知點的平面坐標(biāo)、大地高和正常高的數(shù)據(jù)按最小二乘法求解系數(shù)K。根據(jù)式(4)計算未知點的相對正常高高程異常的步驟如下：

1)明確測區(qū)已知點的個數(shù)，來確定式(4)中的系數(shù)K的個數(shù)，K的個數(shù)要少于已知點的個數(shù)。

2)在測區(qū)里選定一個起始點，計算其他已知點相對起始點的相對大地高高程、相對正常高高程和相對正常高高程異常，再利用間接平差按最小二乘法求解系數(shù)K。

3)計算待擬合點相對于起始點的相對大地高Δh起始點到未知點，然后代入式(4)中可求得待擬合點相對起始點的相對正常高高程異常。

3.GPS相對大地高轉(zhuǎn)化為相對正常高

求解待定點相對于起始點的相對正常高高程異常后，通過式(2)求得待定點相對起始點的相對正常高，即

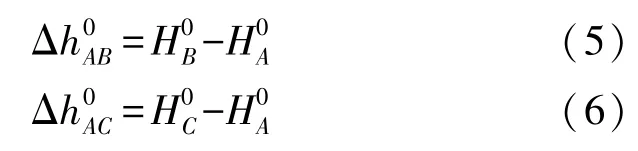
利用式(5)—式(6)就可以得到B、C兩點的相對正常高。這樣就能把待定點相對于起始點的相對正常高轉(zhuǎn)化為任意兩個待定點間的相對正常高。

4.相對正常高求解正常高高程

求得的兩點間相對正常高和已知點的正常高高程數(shù)據(jù)按下列公式計算就得到待定點的正常高高程。

上式求出的待定點的正常高高程，由于待定點可以由不同的已知點來推求，這樣就存在多余觀測數(shù)據(jù)，利用平差計算優(yōu)化待定點的正常高高程解。

三、實例數(shù)據(jù)分析

為了驗證相對正常高高程異常的GPS高程擬合方法的可行性，本文采用二次曲面擬合的方法進行比較驗證。某山區(qū)測區(qū)控制點共有15個，控制點的示意圖如圖1所示，在該區(qū)選取了平均對稱的7個已知點，具體數(shù)據(jù)見表1，其余8個點作為待擬合點，具體數(shù)據(jù)見表2。

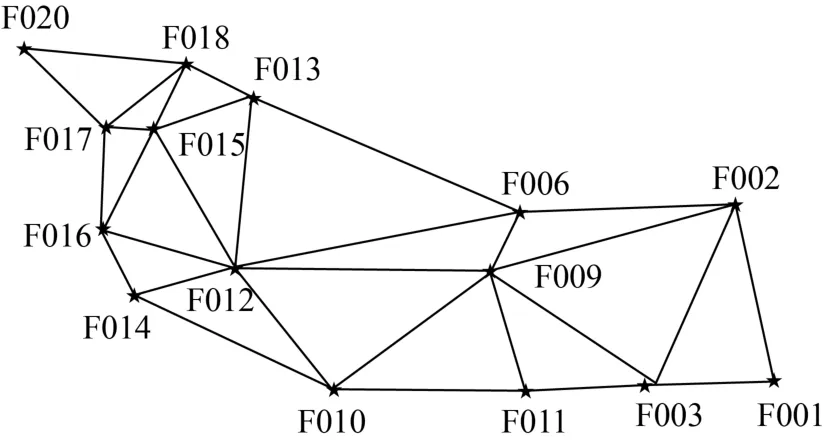
圖1 山區(qū)GPS控制點示意圖

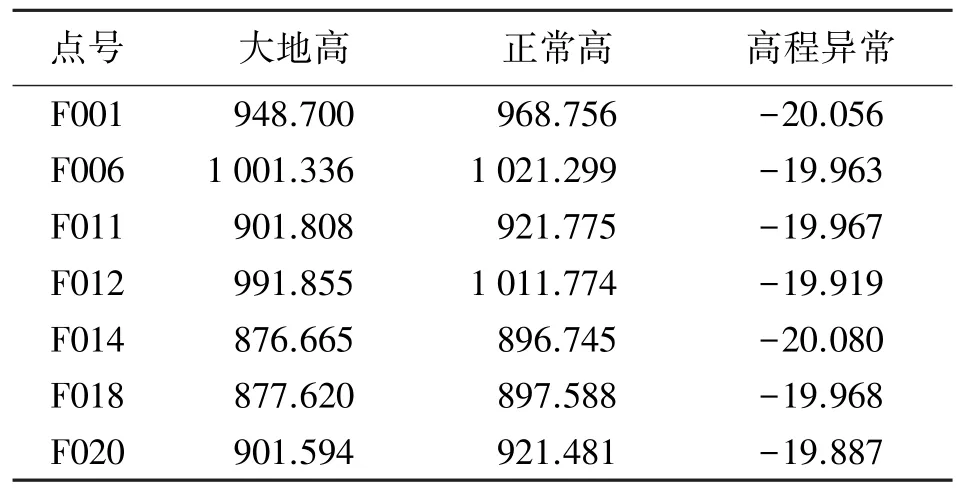
表1 7個已知點的數(shù)據(jù) m

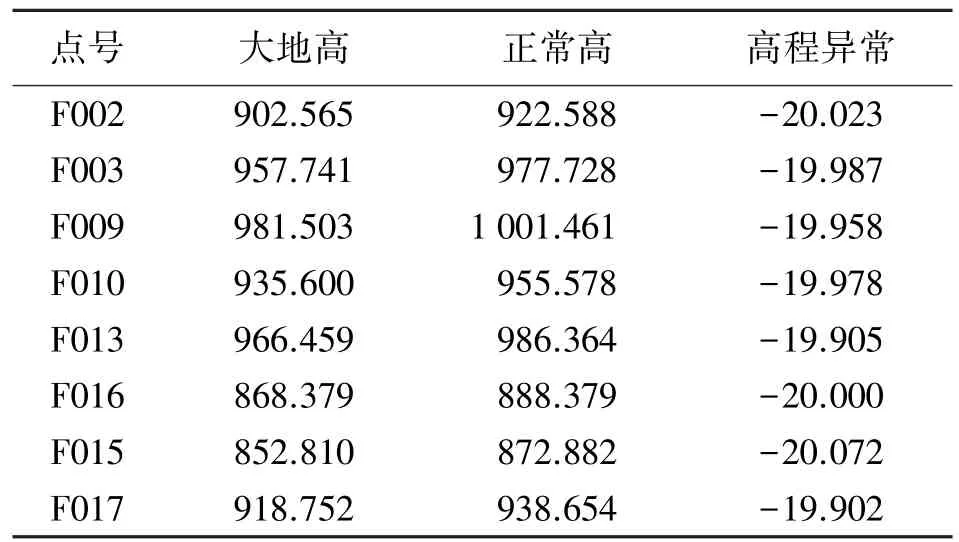
表2 8個待擬合點的數(shù)據(jù) m

1.利用二次曲面進行GPS高程擬合

采用二次曲面擬合，用Matlab 7.0實現(xiàn)其算法，得到了8個待擬合點的正常高(見表3)，內(nèi)部符合

精度為1.4 cm，外部符合精度為23.0 cm。

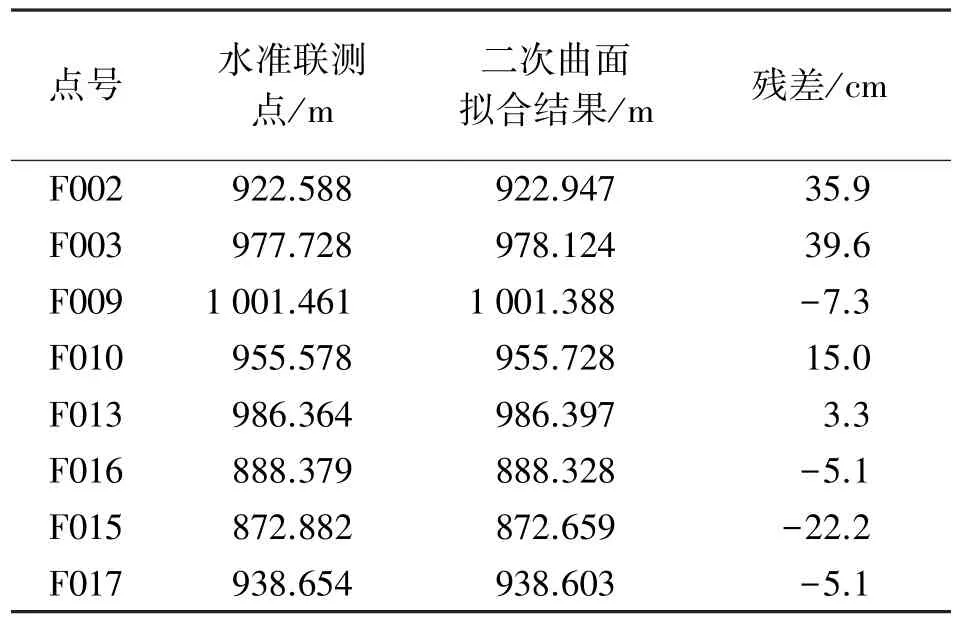
表3 二次曲面擬合結(jié)果

2.基于相對正常高高程異常的GPS高程擬合

選取F012作為起始點，根據(jù)待擬合點和已知點組合的控制網(wǎng)模型，列出間接平差方程，求解待擬合點的正常高見表4，其內(nèi)部符合精度為4.3 cm，外部符合精度為2.74 cm。3.二次曲面擬合與相對正常高高程異常擬合對比

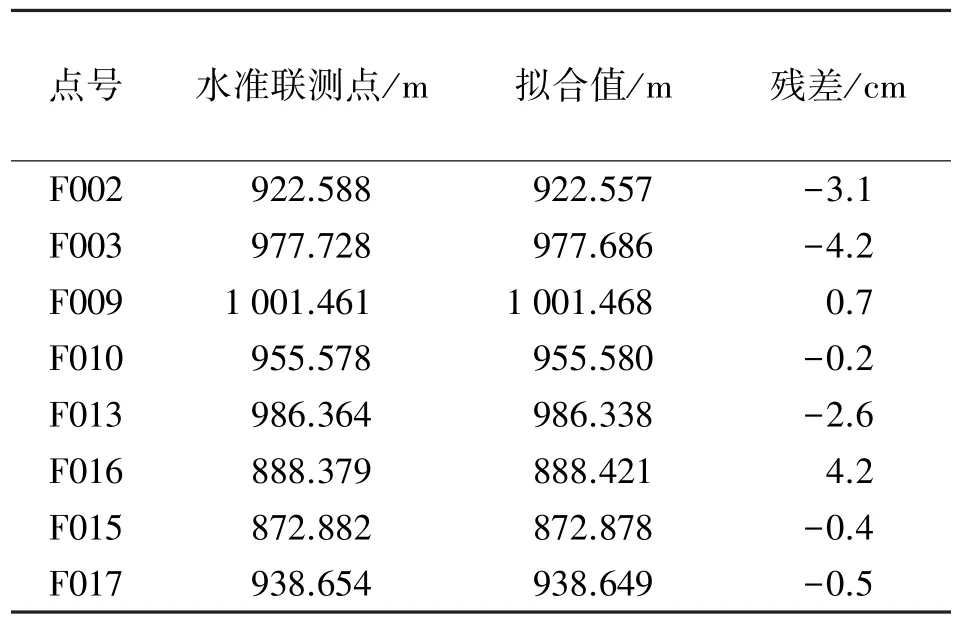
表4 8個待擬合點結(jié)果

由表3、表4可以明顯地看出，利用相對正常高高程異常的GPS高程擬合得到的待定點的精度好于傳統(tǒng)的二次曲面擬合，其最大的殘差為4.2 cm。測區(qū)的GPS點之間的平均邊長在2 km左右，最大殘差為4.2 cm，在普通幾何水準(zhǔn)測量誤差允許殘差范圍內(nèi)。在地勢起伏較大的地區(qū)應(yīng)用二次曲面擬合，其精度有的很差。從表中可以看出，二次曲面擬合的內(nèi)符合精度很高但外符合精度很低，這是由于山區(qū)的高程異常變化大所決定的。

通過對比，充分地說明了基于相對正常高高程異常的GPS高程擬合在處理山區(qū)的數(shù)據(jù)時能明顯地提高GPS高程擬合的精度。

四、結(jié)束語

傳統(tǒng)的GPS高程擬合依賴于已知點平面位置數(shù)據(jù)，而沒有考慮到高程異常值與地面高低起伏之間的關(guān)系。本文在進行高程擬合時不僅考慮了高程異常與平面的位置間的關(guān)系，而且還考慮了與地面的起伏高差之間的關(guān)系，在傳統(tǒng)二次曲面GPS高程擬合的基礎(chǔ)上，通過增加一個相對大地高擬合變量，提出了基于相對正常高高程異常的GPS擬合方法，并通過某山區(qū)工程實例驗證了此方法的可行性，同時也驗證了采用此方法的擬合精度比傳統(tǒng)二次曲面的GPS高程擬合精度要高。

[1] 張正祿，鄧勇，羅長林，等.利用GPS精化區(qū)域似大地水準(zhǔn)面[J].大地測量與地球動力學(xué)，2006，26(4)：14-17.

[2] 張小紅，程世來，許曉東.基于Kriging統(tǒng)計的GPS高程擬合方法研究[J].大地測量與地球動力學(xué)，2007，27(2)：47-51.

[3] 楊江波，李為樂，余代俊，等.GPS高程擬合方法的實驗研究[J].測繪科學(xué)，2009，34(3)：54-57.

[4] 黃祥雄，廖超明，曾教勝，等.區(qū)域精化似大地水準(zhǔn)面在工程三維GPS控制網(wǎng)建設(shè)中的應(yīng)用研究[J].測繪通報，2010(2)：35-37.

[5] 楊明清，靳蕃，朱達成，等.用神經(jīng)網(wǎng)絡(luò)方法轉(zhuǎn)換GPS高程[J].測繪學(xué)報，1999，28(4)：301-307.

[6] 劉俊領(lǐng)，劉海生，王衍靈，等.GPS高程擬合方法研究[J].測繪與空間地理信息，2009，32(1)：143-147.

[7] 魏立峰，何建國.GPS高程擬合似大地水準(zhǔn)面的方法[J].地理空間信息，2010，8(4)：72-73.

[8] 李秀海.平坦地區(qū)GPS高程擬合方法精度分析[J].黑龍江工程學(xué)院學(xué)報：自然科學(xué)版，2009，23(4)：4-6.

[9] 陳本富，王貴武，沈慧，等.基于Matlab的數(shù)據(jù)處理方法在GPS高程擬合中的應(yīng)用[J].昆明理工大學(xué)學(xué)報：理工版，2009，34(5)：1-4.

[10] 高寧，高彩云，吳良才.GPS高程迭加擬合模型的研究[J].西安科技大學(xué)學(xué)報，2009，29(3)：339-343.

[11] 吳曉平.似大地水準(zhǔn)面的定義及在空中測量中涉及的問題[J].測繪科學(xué)，2006，31(6)：24-25.

Discussion on the Relative Height Anomaly of GPS Elevation Fitting Method

CHEN Yanhong，MA Quanming，LIU Ruimin，MAO Xiaokang

P228.4

B

0494-0911(2014)12-0067-03

陳艷紅，馬全明，劉瑞敏，等.基于相對高程異常的GPS高程擬合方法探討[J].測繪通報，2014(12)：67-69.

10.13474/j.cnki.11-2246.2014.0400

2014-01-08

陳艷紅(1977—)，女，河北阜城人，碩士，講師，主要從事大地測量數(shù)據(jù)處理的研究與工作。