非磁性次級直線感應(yīng)電機力特性及渦流損耗分析

李碩， 范瑜， 呂剛， 李華偉

(北京交通大學(xué)電氣工程學(xué)院，北京100044)

0 引言

磁懸浮列車是一種新型地面無接觸高速交通運輸工具，具有無污染、噪音小、能耗低、安全性高等特點［1］。但其鋪設(shè)成本高，維護復(fù)雜，與既有線路不兼容等局限性，不適合大規(guī)模推廣。

本文所研究的非磁性次級直線感應(yīng)電機屬于電動式磁懸浮系統(tǒng)。在電機初級繞組中通入三相對稱交變電流產(chǎn)生運動的行波磁場，該磁場與非磁性次級導(dǎo)體中感應(yīng)出的渦流磁場相互作用產(chǎn)生懸浮力，同時又可以提供驅(qū)動力［2］。

目前研究電動式磁懸浮系統(tǒng)以永磁電動式為主，如美國威斯康辛州立大學(xué)的 T.A.Lipo教授［3-4］及日本九州大學(xué)的藤井信南教授［5-6］都對永磁電動式磁懸浮系統(tǒng)進行了深入研究，但目前尚處于實驗室研究階段。永磁電動式磁懸浮系統(tǒng)產(chǎn)生懸浮力需要附加的推進系統(tǒng)使永磁體與非磁性導(dǎo)體板相對運動，存在附加的推進系統(tǒng)將產(chǎn)生很大的機械振動及機械噪聲大等缺點。

非磁性次級直線電動式磁懸浮系統(tǒng)通過運動磁場相互作用可同時提供推進力和懸浮力，相對于永磁電動式磁懸浮具有不需要附加的推進系統(tǒng)，可避免產(chǎn)生機械振動，整體總量輕等優(yōu)點。與現(xiàn)有復(fù)合次級直線牽引電機相比，由于采用非磁性次級，電機法向力不再是吸引力而表現(xiàn)為懸浮力，在實際運行中，在一定范圍內(nèi)可減輕車體重量，提高運載能力。

為了深入了解非磁性次級直線電機的性能特性，本文從經(jīng)典電磁場理論分析出發(fā)，建立了非磁性次級直線感應(yīng)電機的簡化二維電磁模型，并對其磁場進行了分析，得到該電機的推進力、懸浮力及次級渦流損耗解析表達式;得到了推進力、懸浮力及次級渦流損耗的特性曲線。研究了次級損耗與輸入電流幅值、頻率、轉(zhuǎn)差率之間的關(guān)系，找出較合適的工作區(qū)間。通過樣機實驗來驗證理論分析的正確性。

1 電機的電磁模型

非磁性次級直線感應(yīng)電機示意如圖1所示。電機由初級鐵心、繞組及非磁性次級(鋁板)構(gòu)成。考慮到非磁性次級直線感應(yīng)電機的結(jié)構(gòu)特點，建立其二維電磁場模型可有效減少計算量。

假定電機初級鐵心磁導(dǎo)率無窮大;氣隙磁場強度在z軸方向均勻恒定;電機初級鐵心在x軸方向與次級相對運動，y軸為懸浮方向。并用表面電流層代替初級磁勢，僅考慮基波分量忽略諧波影響。邊端效應(yīng)及齒槽效應(yīng)通過卡氏系數(shù)進行修正［7］，即

式中:g為裝置氣隙長度;ge為考慮了各種主要影響因素的等效氣隙長度;Kc為消除初級開槽對氣隙中磁場分布造成影響的卡氏系數(shù);Kg為消除磁場分布y方向上分布不均的波形畸變系數(shù);Kt為補償裝置橫向邊端效應(yīng)的橫向邊端效應(yīng)系數(shù)。

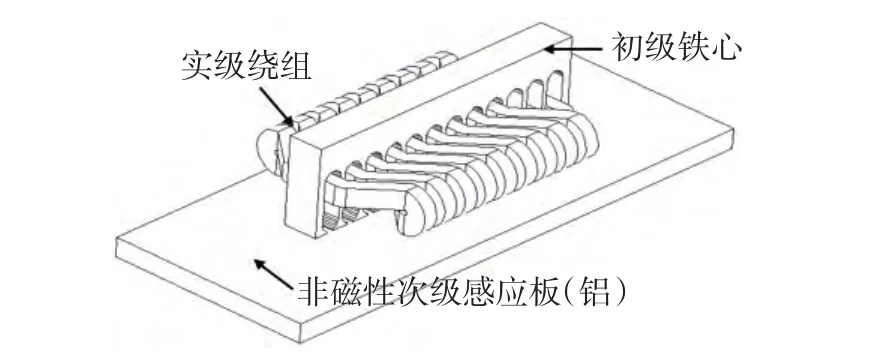
圖1 非磁性次級直線感應(yīng)懸浮電機示意Fig.1 The scheme of non-magnetic secondary linear induction maglev motor

基于以上假設(shè)，在笛卡爾坐標(biāo)系內(nèi)，將參考坐標(biāo)固定在初級鐵心上，建立非磁性次級直線感應(yīng)電機的二維電磁分析模型，如圖2所示。

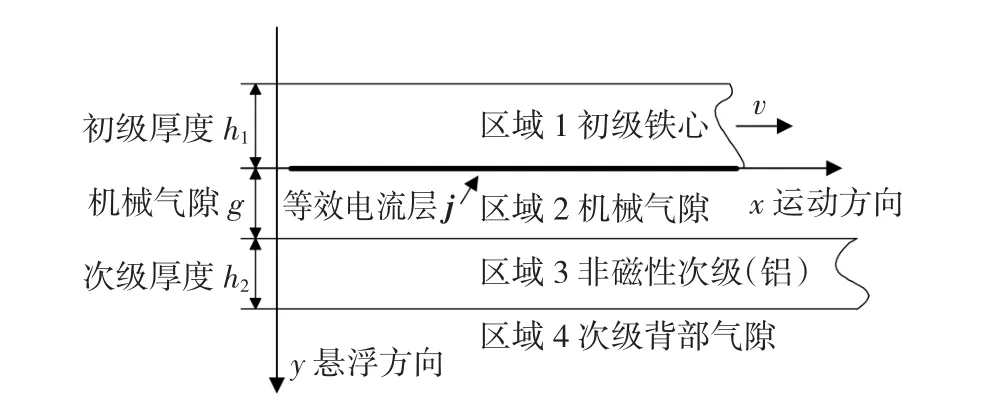
圖2 電機二維電磁分析模型Fig.2 2D electromagnetic analysis model of the motor

將分布繞組等效為電流層，初級電流層j在區(qū)域1和區(qū)域2之間，在電機初級表面。其表現(xiàn)形式［8-11］為

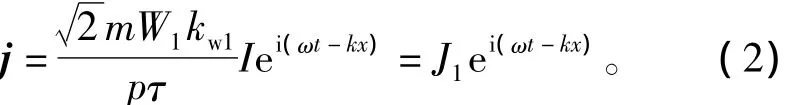
式中:m為初級繞組的相數(shù);W1為初級繞組每相串聯(lián)匝數(shù);kw1為初級繞組系數(shù);p為初級繞組極對數(shù);I為初級相電流有效值。

從穩(wěn)態(tài)麥克斯韋基本電磁場理論出發(fā)［12～15］，則有

由歐姆定律得

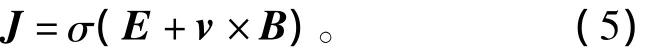
結(jié)合式(3)～式(5)可得二階偏微分方程為

根據(jù)初級表面電流分布的周期性邊界條件，磁場B具有x、y分量，次級渦流在z方向流動，B、J可具有如下形式，即

將式(7)代入式(6)得

其中，Q2=k2+ikμσv，μ、σ、v 分別為磁導(dǎo)率、電導(dǎo)率、行波線速度。式(8)和式(9)的通解為

由于不同區(qū)域的介質(zhì)條件不同，需分別求解。區(qū)域 1 中，σ1=0，μ1= μFe，Q1=k，可得

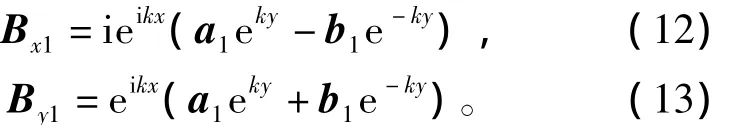
區(qū)域2 中，σ2=0，μ2= μ0，μ0=4π ×10-7N/A2為真空磁導(dǎo)率，Q2=k，可得

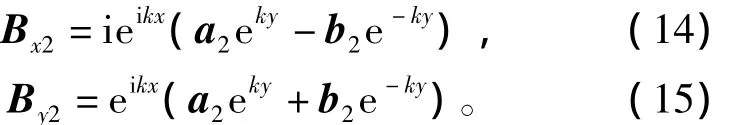
區(qū)域 3 中，σ3= σAl=3.8 ×107S/m，μ3= μ0，可得

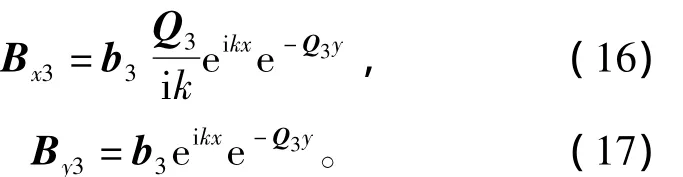
根據(jù)分界面邊界條件，可確定以下方程，即

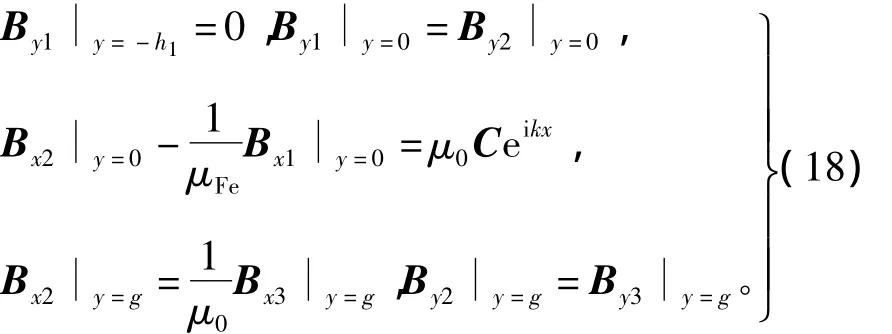
確定待定系數(shù) a1、a2、b1、b2、b3為

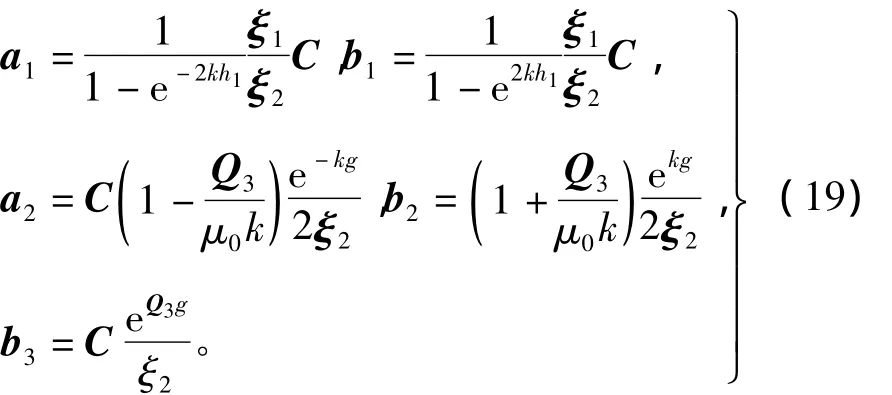
g為機械氣隙高度;h1為初級鐵心厚度。

2 力特性及損耗計算

由麥克斯韋張量法可確定次級所受到的推力及懸浮力，即

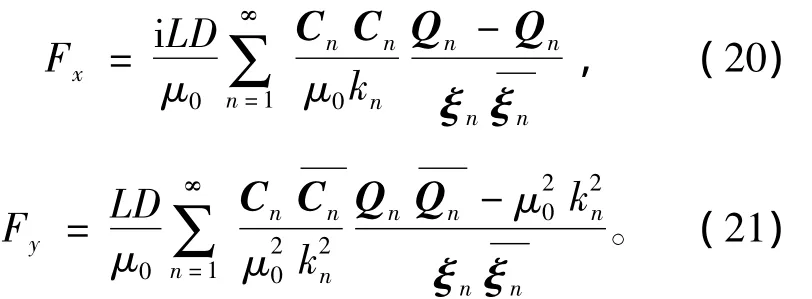
式中:L為電機長度;D為電機寬度;n為磁場諧波次數(shù)。

次級的渦流損耗為

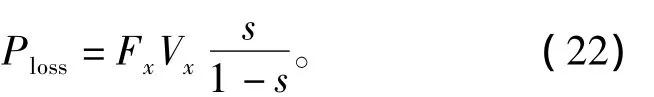
式中，Vx=2τf(1-s)為電機推進速度。

3 實驗平臺及特性分析

3.1 實驗平臺及參數(shù)設(shè)計

本直線感應(yīng)電機實驗平臺主要包括直線電機本身與車載系統(tǒng)、數(shù)據(jù)采集系統(tǒng)、控制系統(tǒng)3部分。直線電機安放在輪軌車輛底部，與實驗臺板上拼接布置的非磁性感應(yīng)板相對。車輛可沿軌道行走。通過調(diào)節(jié)的車體懸掛上的螺栓，可以調(diào)節(jié)氣隙大小。推力可通過安裝在車后部的傳感器1測得。懸浮力可通過車體上傳感器2、傳感器3協(xié)同測得。非磁性次級直線電機極數(shù)為 4，極距為42 mm，槽寬為11 mm，槽高為 28.72 mm，軛部高為 25.78 mm，鐵心寬度為 11 mm，繞組匝數(shù)為 150，次級鋁板厚為15 mm，氣隙在1～20 mm范圍內(nèi)調(diào)整。電機工作電壓為380 V，最大電流為8 A。

圖3 直線感應(yīng)電機實驗平臺Fig.3 Photo of experimentation vehicle

3.2 理論計算及實驗驗證

利用式(20)～式(22)可計算出電機的推力、懸浮力及次級渦流損耗，并利用Ansoft有限元軟件及實驗平臺進行有限元分析及實驗驗證。

圖4為不同幅值下電機可產(chǎn)生的推力圖。由圖4可知，轉(zhuǎn)差率為1時，電流幅值在4 A、6 A和8 A的條件下，電機推力隨著電源頻率先增大后減小。在20～40 Hz之間可達到最大值。由此可見，電機在低頻段可輸出較大推力。

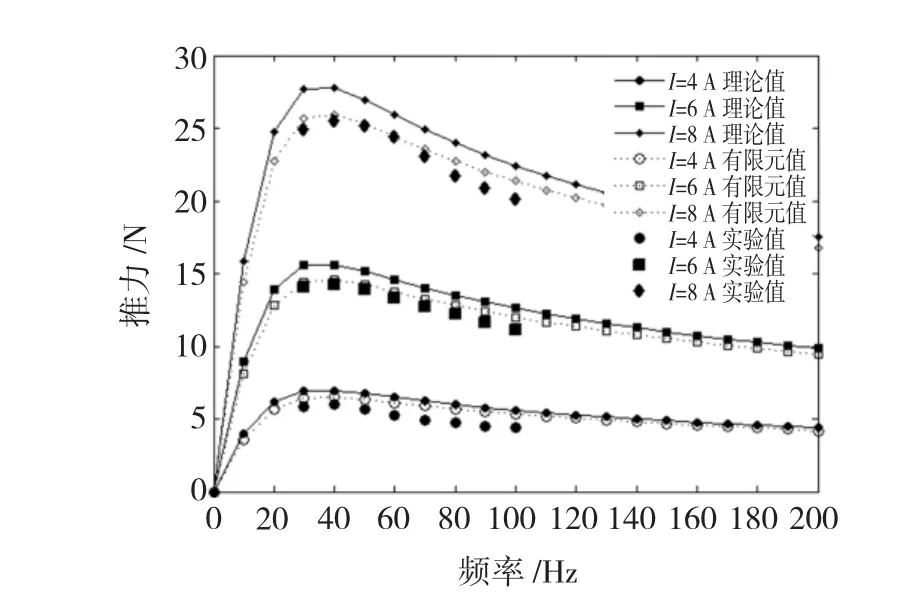
圖4 不同電流幅值下的推力Fig.4 Thrust force curve under different current

圖5為在電流幅值恒定，不同頻率的條件下，電機的推力與轉(zhuǎn)差率之間的關(guān)系。由圖5可知，電機的推力隨轉(zhuǎn)差率先增大后減小。在120 Hz條件下，推力最大值出現(xiàn)在轉(zhuǎn)差率為0.2～0.3之間。而在30 Hz條件下，推力最大值出現(xiàn)在轉(zhuǎn)差率為0.6～1之間。

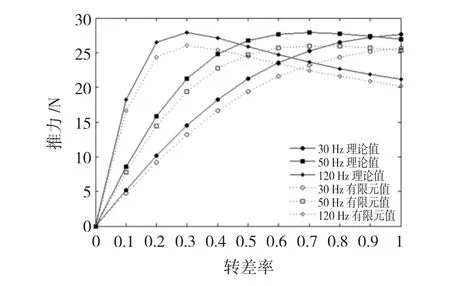
圖5 不同轉(zhuǎn)差率下的推力Fig.5 Thrust force curve under different slip

圖6為考察電流分別在4 A、6 A及8 A條件下，不同頻率電機輸出懸浮力特性。懸浮力與頻率呈單調(diào)上升關(guān)系。當(dāng)頻率增加到100～140 Hz后，懸浮力增加趨勢變緩。理論值、有限元值與實驗值之間的平均誤差分別為 7.2%和 4.3%，均滿足工程需要。

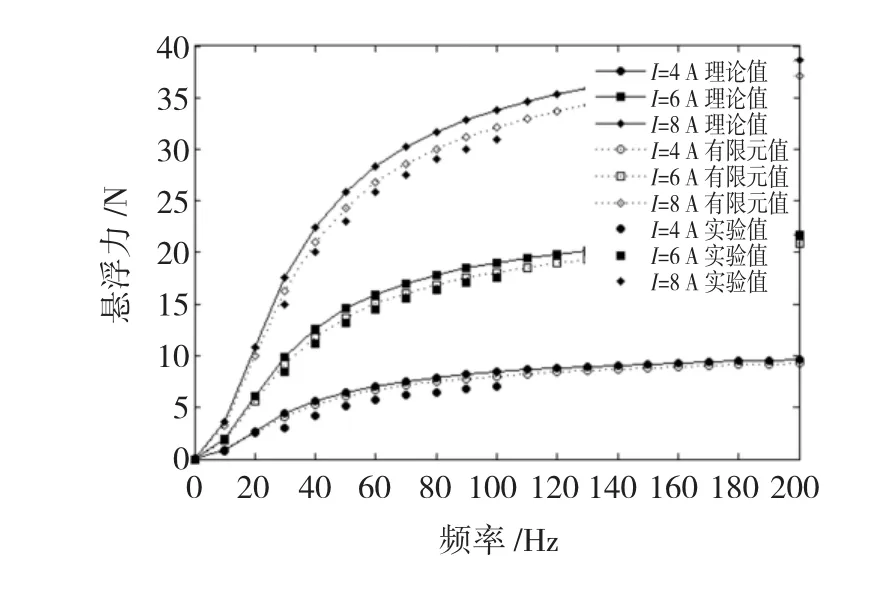
圖6 不同電流幅值下的懸浮力曲線Fig.6 Levitation force curve under different current

圖7為不同轉(zhuǎn)差率時懸浮力變化曲線。由圖7可知，在電流幅值恒定，不同頻率的條件下，電機的懸浮力隨轉(zhuǎn)差率單調(diào)增加。在轉(zhuǎn)差率為1時(堵轉(zhuǎn)時)達到最大值。

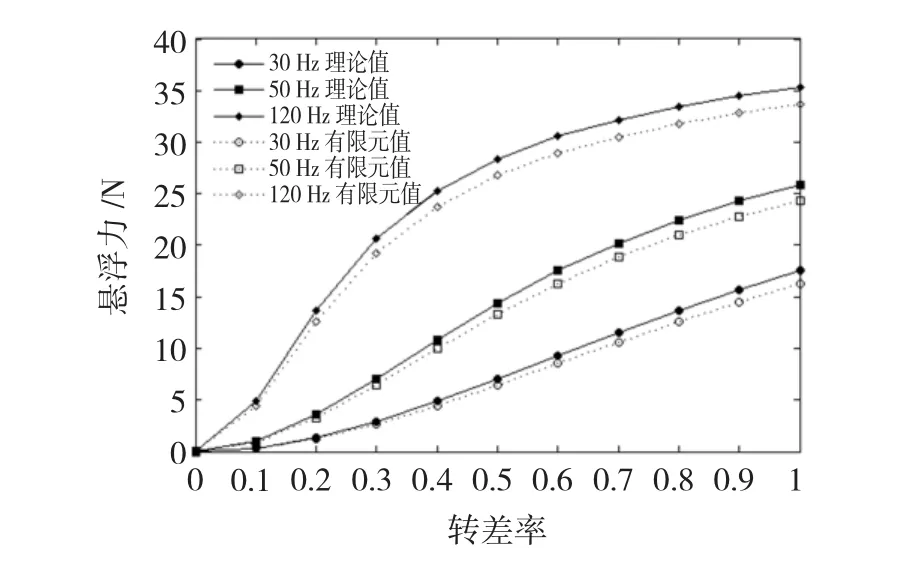
圖7 不同轉(zhuǎn)差率下的懸浮力Fig.7 Levitation force curve under different slip

圖8為電流幅值0～8 A，頻率0～200 Hz范圍內(nèi)次級渦流損耗三維特性曲線。由圖8可知，電機次級渦流損耗隨電流幅值呈平方關(guān)系快速增加;隨頻率增加單調(diào)增加，但在高頻段增加趨勢放緩。次級損耗隨頻率變化趨勢與懸浮力隨頻率變化趨勢十分接近，這是由于懸浮力主要由次級內(nèi)部渦流磁場產(chǎn)生。此結(jié)果與文獻［14］結(jié)論相似。圖9為不同轉(zhuǎn)差率下，次級渦流損耗變化曲線。由圖9可知，次級渦流損耗隨轉(zhuǎn)差率單調(diào)遞增。當(dāng)轉(zhuǎn)差率小于0.3時，即高速運行時，渦流損耗增加較為平緩;當(dāng)轉(zhuǎn)差大于0.3時，損耗增加速度要明顯加快，最大值出現(xiàn)在轉(zhuǎn)差率為1附近。此外，高頻條件下的渦流損耗遠大于低頻段的損耗。這說明單從損耗方面考慮，該類電機應(yīng)工作在中高速范圍內(nèi)，這樣可以有效降低次級損耗，提高工作效率。因此，在實際應(yīng)用中，根據(jù)不同工況應(yīng)找出合適的工作點，如在中低速工況下，可選擇低頻大電流條件，此時既可實現(xiàn)較大推力和一定的懸浮力，而次級渦流損耗相對較小。

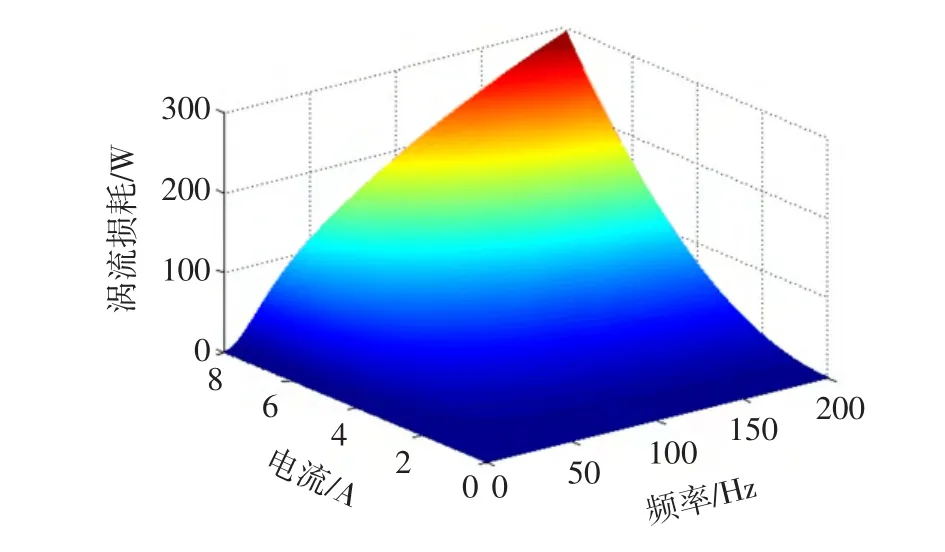
圖8 不同電流幅值、頻率下的次級渦流損耗曲線Fig.8 Eddy loss curve under different current and frequency

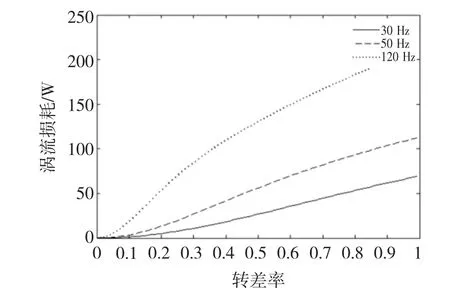
圖9 不同轉(zhuǎn)差率下的次級損耗Fig.9 Eddy loss curve under different slip

4 結(jié)語

本文研究了非磁性次級直線感應(yīng)電機的基本原理，以麥克斯韋電磁方程為基礎(chǔ)，建立了直線感應(yīng)電機的簡化二維電磁模型，并對其磁場進行了分析，得到了該電機的推進力、懸浮力及次級渦流損耗的解析表達式。非磁性次級直線感應(yīng)電機與常規(guī)復(fù)合次級直線感應(yīng)電機相比，其法向力表現(xiàn)為懸浮力，這樣在實際運行中，可以減輕車體有效重量，提高運載能力。在輸入電流一定的條件下，若以輸出推力、效率為目標(biāo)，電機應(yīng)工作在低頻段;若以輸出懸浮力為目標(biāo)，電機應(yīng)工作在高頻段。

［1］ YAN Luguang.Development and application of the magnet technology in China［C］//MT 15 Conference，Beijing，October.1997.

［2］ CHEN Yaowming，F(xiàn)AN Shuyuan，LU Wieshin.Electromagneticforce analysis of the magnetically levitated motor with two directions of movement［J］.IEEE Transactions on Industry Applications，2006，42(1):31-41.

［3］ BIRD Jonathan，LIPO Thomas A.A 3-D magnetic charge finiteelement model of an electrodynamic wheel［J］.IEEE Transactions on Magnetics，2008，44(2):253-265.

［4］ BIRD Jonathan，LIPO Thomas A.Characteristics of an electrodynamic wheel using a 2-D steady-state model［J］.IEEE Transactions on Magnetics，2007，43(8):3395-3405.

［5］ FUJII N，OGAWA K，CHIDA M.Three dimensional force of magnet wheel with revolving permanent magnets［J］.IEEE Transactions on Magnetics，1997，33(5):4221-4223.

［6］ FUJII N，NONAKA S，HAYASH G.Design of magnet wheel integrated own drive［J］.IEEE Transactions on Magnetics，1999，35(5):4013-4015.

［7］ 張廣溢.直線電機靜態(tài)橫向邊端效應(yīng)研究［J］.電機與控制學(xué)報，1999，3(2):126-128.

ZHANG Guangyi.Research on the static transverse end effect of the linear motor［J］.Electric Machines and Control，1999，3(2):126-128.

［8］ 朱熙，范瑜，呂剛，等.單邊盤式感應(yīng)電機的數(shù)學(xué)模型與轉(zhuǎn)矩分析［J］.中國電機工程學(xué)報，2010，30(24):69-74.

ZHU Xi，F(xiàn)AN Yu，Lü Gang，et al.Modeling and torque analysis of a disc induction motor［J］.Proceedings of the CSEE，2010，30(24):69-74.

［9］ 朱熙，范瑜，李碩，等.旋轉(zhuǎn)磁場電動式磁懸浮裝置的狀態(tài)方程與懸浮力控制［J］.電工技術(shù)學(xué)報.2011，26(12):1-6.

ZHU Xi，F(xiàn)AN Yu，LI Shuo，et al.State equations and lift force control of rotating field electrodynamic levitation device［J］.Transactions of China Electrotechnical Society，2011，26(12):1-6.

［10］ 秦偉，范瑜，呂剛，等.非磁性次級感應(yīng)懸浮電機磁場和力特性研究［J］.電機與控制學(xué)報，2011，15(8):1-6.

QIN Wei，F(xiàn)AN Yu，Lü Gang，et al.Characteristic and magnetic field analysis non-magnetic secondary induction maglev motor［J］.Electric Machines and Control，2011，15(8):1-6.

［11］ LI Shuo，F(xiàn)AN Yu，ZHU Xi，et al.New structure of axial flux induction motor and characterization analysis［C］//2011 International Conference on Electrical Machines and Systems，August 20-23，2011，Beijing，China.2011:6073906.

［12］ SUN Yanhua，YU Lie.Eddy current effects on radial active magnetic bearings with solid rotor［C］//8th International Symposium on Magnetic Bearing，August 26-28，2003，Mito，Japan，2003.

［13］ SUN Yanhua，YU Lie.Analytical method for eddy current loss in laminated rotors with magnetic bearings［J］.IEEE Transactions on Magnetics，2002，38(2):1341-1347.

［14］ 朱熙，范瑜，秦偉，等.旋轉(zhuǎn)磁場電動式磁懸浮裝置的力和損耗特性分析［J］.中國電機工程學(xué)報，2012，35(12):90-96.

ZHU Xi，F(xiàn)AN Yu，QIN Wei，et al.Force and loss characteristic analysis of rotating field electro-dynamic levitation devices［J］.Proceedings of the CSEE，2012，35(12):90-96.

［15］ 李碩，范瑜，朱熙，等.軸向磁通懸浮感應(yīng)電機的特性研究與實驗［J］.電工技術(shù)學(xué)報，2012，27(9):204-209.

LI Shuo，F(xiàn)AN Yu，ZHU Xi，et al.Characteristics of an axial flux induction maglev motor and experiment［J］.Transactions of China Electrotechnical Society，2012，27(9):204-209.