負阻抗補償法在機電作動器上的研究與應用

王娜， 周元鈞

(北京航空航天大學自動化科學與電氣工程學院，北京100191)

0 引言

在多電飛機的270V高壓直流供電系統中，功率電子裝置驅動的電動機負載和變換器類負載顯著增加。航空機電作動器(electromechanical actuator，EMA)作為其中的典型負載之一，由于閉環控制而具有恒功率負載(constant power loads，CPLs)特性。恒功率負載具有負阻抗特性，該特性會給供電系統的穩定運行帶來負面影響［1-10］。另一方面，連接在航空直流供電網絡上的電力傳動系統，當采用PWM控制時必須考慮電磁兼容問題，一般采取在直流母線輸入端必須加LC濾波器的方法［1，8-13］。

目前對于穩定性的研究，主要分為大信號方法和小信號方法兩大類。根據Brayton-Moser混合勢函數理論［8］，在選定濾波諧振頻率的情況下選取較大的濾波電容值，可實現系統在大擾動下的穩定性。但電容過大會導致電源合閘時大電流浪涌，這是航空電源所不希望的。另一方面，對于大容量的電容要求，如果采用電解電容會降低系統的可靠性，這也是航空設備所不希望的，同時不滿足國軍標航空系統特性中對于可靠性及瞬態電流的要求［16］。針對以上弊端，有研究者［11-14］根據Middlebrook阻抗比定理，采用無源阻尼的方法，在LC濾波電路中加入阻尼電路來抑制系統的。然而當阻尼電阻與電感串聯時，阻尼電阻中會流過幾乎所有的直流電流而降低效率;當阻尼電阻與電容串聯時，則會流過幾乎所有交流電流而嚴重影響濾波器的衰減特性及效率。還有文獻［16-18］針對CPL的特殊負載特性，提出設計具有高性能魯棒性的控制器，通過Lyapunov穩定性判據來解決系統穩定性問題。但是這類大信號分析方法引用復雜的非線性方程，要么控制器參數與系統參數有關，要么實現復雜，或者不滿足快速性和可靠性要求，不能形成通用的控制算法，因而在實際應用中存在一定的局限性。

文獻［19］提出一種負阻抗補償法，它在母線電壓上引入高頻濾波器后，在保持恒功率特性的同時，使系統具有正導納值，提高系統的穩定性。此方法基于小信號理論推導補償器參數設計，通過勞斯判據保證穩定性，但是對于具有高性能指標的航空機電作動器而言，單純的穩定性并不能保證良好的系統性能。因此還應在保證穩定性的同時，兼顧系統性能，以實現最優設計。

針對上述問題，本文研究該方法在航空機電作動器中的應用，由于航空機電作動器是一種存在大擾動的伺服控制系統，因此在補償器的設計中，除保證系統穩定性外，還研究了補償器對系統動態性能的影響，要求最大限度提高系統抗干擾能力。

1 系統建模及補償器的設計

以270 V航空高壓直流電源帶載的電力作動器為研究對象，其系統結構如圖1所示。直流電源經EMI濾波，通過雙極性逆變器對5 kW無刷直流電機(BLDCM)供電。轉速環和電流環均為傳統的帶限幅的PI調節器，位置環為比例調節。反饋電流是對母線電流采樣而得。參考電流由轉速調節器ASR輸出和改進型負阻抗補償器(modified negative input-resistance compensator，MNIRC)輸出兩部分組成。MNIRC補償器公式為

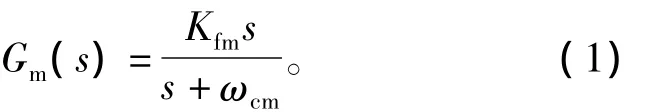
式中:Kfm為高頻增益;ωcm為轉折頻率。而增大電容法改善系統穩定性是通過增大圖1中Cs電容值來實現的。

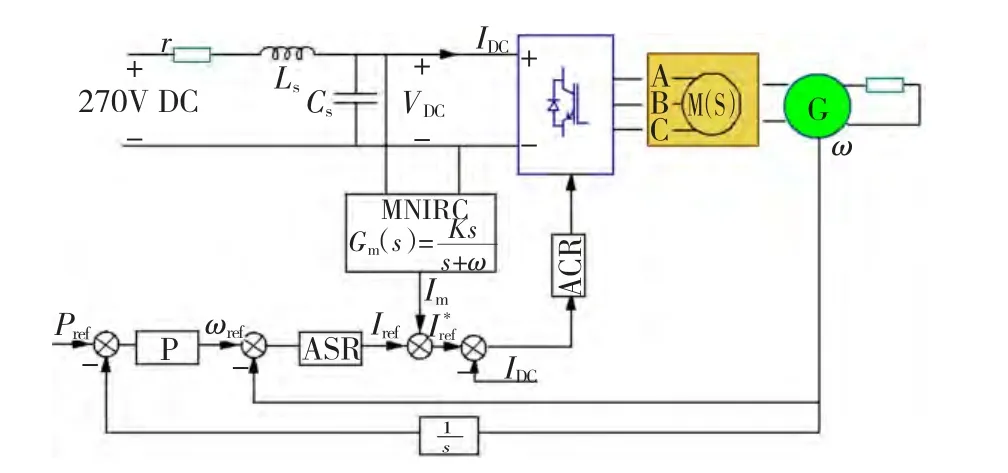
圖1 帶有補償器的系統結構圖Fig.1 Diagram of system with compensator

1.1 系統的輸入導納推導

定義系統輸入導納為由逆變器前直流端向逆變器側看去的導納值。保證這部分系統在動態模型時的導納值為正，便能消除由閉環系統帶來的負阻抗效應。

1.1.1 逆變器模型的建立

大功率逆變器具有非線性，建模時采用平均模型法，并將其進行小信號線性化處理。母線電壓Vdc和PWM波信號決定電機輸入電壓Va。設電機電壓平均值為Va，占空比為d，由于逆變器采用雙極性PWM控制，存在Va=(2d-1)Vdc。因此為計算方便將2d-1記作D，則有

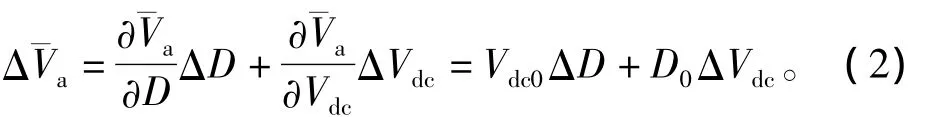
式中:前綴Δ為變量的小信號變量;下標0為變量的穩態值。

同理可得

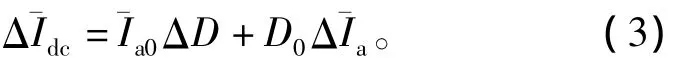
1.1.2 系統傳遞函數

BLDCM電壓方程和轉矩方程可描述為

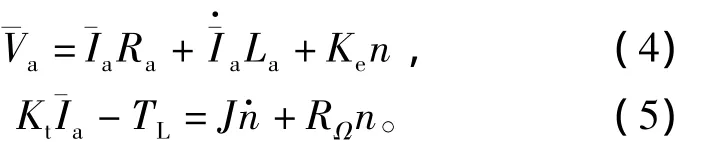
其中:Ra和La分別為電機繞組電阻和電感;Ke和Kt分別為電機反電勢常數和轉矩;n分別為轉子轉動的電角度;TL為負載轉矩;J為轉動慣量;RΩ為旋轉阻尼系數。

將式(4)和式(5)進行Laplace變換，并消去n，可以得到電樞電流的平均值模型為

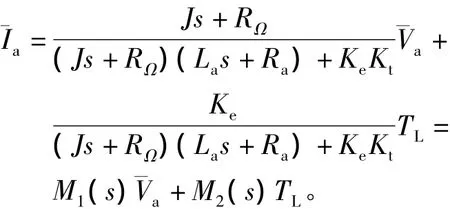
由此可見，電樞電流由電機電壓和負載轉矩共同決定的。

1.1.3 輸入導納的推導

在作動器控制系統中，為了很好地抑制負載干擾，要求電流環響應速度遠高于負載轉矩的變化速度。本補償器設計是在電流環實現的，采用小信號分析時可認為負載轉矩變化ΔTL為0。設電流環的傳遞函數為Gc(s)=Kc(s+zc)/s，根據系統電流環小信號模型可得

利用式(7)消去式(3)和式(8)中ΔD，再重新整理可得

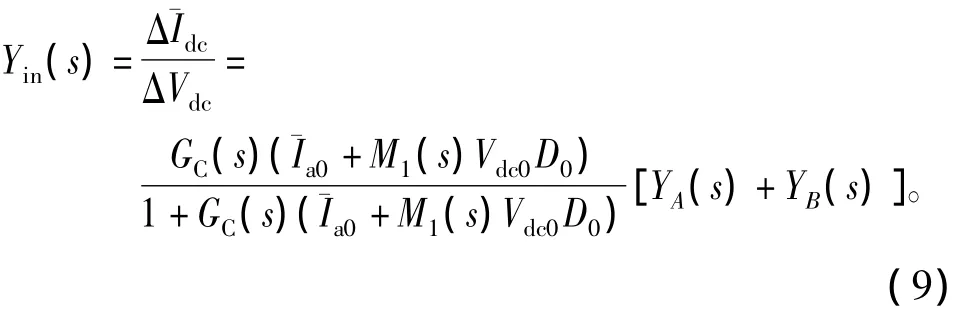
其中，

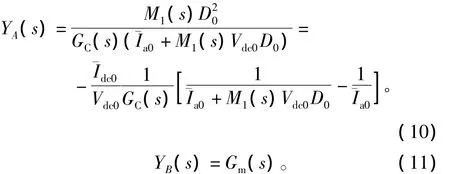
式(9)表明，系統輸入導納由兩部分組成，YA(s)代表系統固有導納，與補償器無關。YB(s)表示補償器修正下的導納。在中頻段，|GC(s)(+M1(s)Vdc0)|≥1，因此系統輸入導納第一項可近似為1。

1.2 改進型負阻抗補償器的設計

補償器應在保證系統穩定性的基礎上，同時滿足系統對快速性及航空直流電源畸變系數小于1%的要求。

將各參數及表達式代入可得

其中

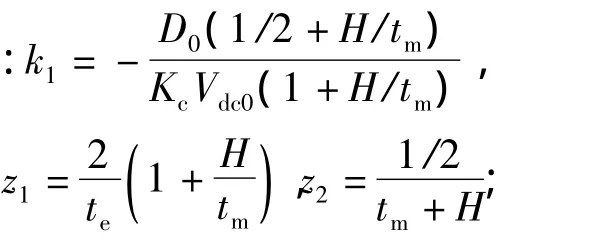
te=La/Ra和tm=JRa/KeKt分別為電機的電磁時間常數和機械時間常數。H=nJ/2TL為轉動慣量常數。

式(12)表明固有導納YA(s)有3個極點，其中z2接近于0，zc和z1間為中頻段，且在中頻段具有負的導納。在中頻段固有導納YA(s)實部為

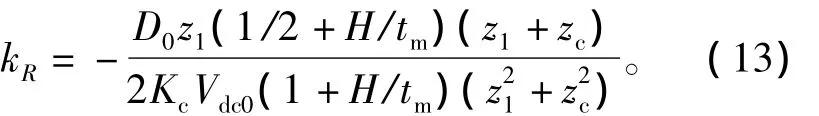
由式(11)可得，YB(s)在中頻段實部為Kfm/2。為使系統具有正的阻抗值，必須滿足YA(s)+YB(s)具有正實部，即

由此可見，高頻增益Kfm越大，系統穩定性越好。同時，為了最大程度衰減輸入濾波器極點震蕩，輸入濾波器固有頻率應選在中頻段，即

為考察系統抗干擾能力，分析加入補償對轉矩的影響，定義直流電壓小擾動時變量變化為其靈敏度傳遞函數。假設負載轉矩恒定，并忽略位置環和速度環，根據小信號模型可得電樞電流靈敏度傳遞函數為

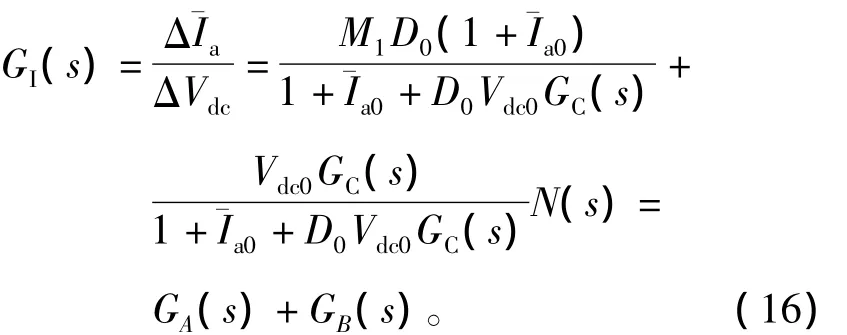
與輸入導納表達式相似，式(16)由兩部分組成，GA(s)代表系統固有靈敏度，GB(s)代表加入補償后對其影響。整理GB(s)可得

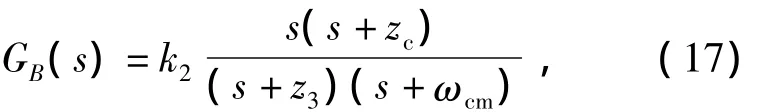
為提高系統抗干擾能力，使GB(s)在中頻段盡可能衰減，系統還應滿足k2＜1，即

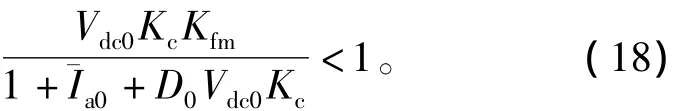
即根據系統對干擾的要求，規定了高頻增益Kfm的上限，因而要求Kfm不能取值太大，進一步限制了補償器參數的范圍，從而在保證系統穩定性的同時，兼顧系統動態性能，提高了系統的抗干擾能力。

1.3 系統穩定性分析

作動器系統濾波器輸出阻抗為Zs，驅動系統輸入阻抗為Zin，則系統總的輸入阻抗值為ZsZin/(Zs+Zin)。根據系統結構圖，可得出總輸入阻抗表達式，其特征方程所有的根均為負，因此滿足勞斯判據，故系統穩定。

2 雙閉環調速系統仿真及性能分析

本文研究的機電作動器的主要參數如表1所示。分別采用增大電容和采用改進型補償器的方法使系統穩定，仿真分析兩種方法控制的系統的動態性能。

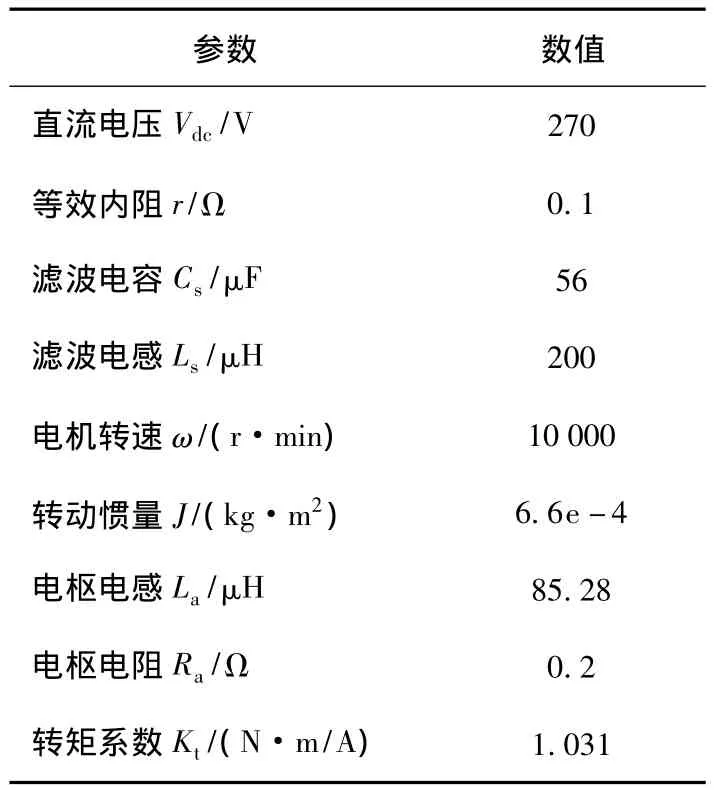
表1 閉環系統主要參數Table 1 Parameters of closed-loop system

將系統參數代入不等式(14)，式(15)和式(18)，可得到 MNIRC的參數應滿足 0.015＜Kfm＜0.93，ωcm＜ωs＜29.4e3。Kfm的增大可減小紋波，但過度增大會加大系統超調，影響系統性能。隨著ωcm的增大，電機轉速超調量減小，調節時間縮短，但是直流側電壓震蕩加劇，增大紋波系數，系統趨于不穩定。綜合考慮，選定補償器參數Kfm為0.3，ωcm為700。

2.1 系統的動態響應

分別對沒有補償器、采用大電容穩定、原負阻抗補償器系統和采用改進型負阻抗補償法的機電作動器系統進行仿真，其動態響應如圖2所示，圖中左側為電網電壓Vdc，右側為電機轉速。圖2(a)是沒有采用補償器的系統響應，雖然快速性比較好，但是由于恒功率的附阻抗特性引起電網電壓的振蕩，調節時間長。由圖2(b)可看出，因增大了濾波電容而增加了電網的穩定性，但是電網合閘時會出現很大的浪涌電流，使電流調節器出現負飽和狀態，進而使電機轉速產生很大的超調。同時太大的容性負載會加重電源負擔，也是航空系統所不允許的。圖2(c)為原負阻抗補償器系統響應，為保證電網電壓的穩定性，需要較大的補償器系數，然而此時電機轉速出現較大超調，因此不能兼顧電網穩定性和系統動態性能。圖2(d)為帶有改進型補償器的系統響應，不僅使電網電壓穩定，電機轉速的快速性和超調都被控制到比較好的程度。

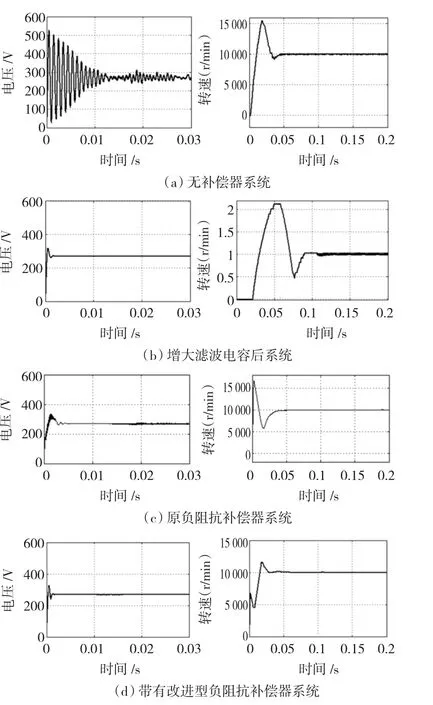
圖2 電機啟動至額定轉速時電網響應比較Fig.2 Performance comparison for starting motor to rated speed

2.2 系統抗干擾性能

圖3給出補償器參數Kfm不同時在0.3 s電機由滿載負載轉矩突卸至空載時的波形。左側為母線電流，右側為電機轉速。可以看出，當選定Kfm為0.3時，對于轉矩大擾動，補償器仍能很好的改進電能質量，減小紋波。但是當高頻增益Kfm增大至超出由抗干擾因素限制的上限時，電機及電網電流均出現不期望的震蕩，從而驗證了對Kfm取值上限進行電機平穩運行。

圖3 負載轉矩大擾動時電機響應Fig.3 Response for large disturbance of load

仿真結果表明，改進型負阻抗補償器可以在不影響電機快速性的情況下，改善電能品質，減小紋波系數。當電網電壓發生擾動，以及對于轉速及負載轉矩大擾動問題，仍然適用。

3 帶補償器的航空作動器系統仿真及實驗

電力作動器是驅動飛機舵面的位置伺服控制系統，運行中轉速、負載變化范圍很大。電力作動器的運行中盡管功率是大幅度變化的，但每個小區間可看作閉環調速系統，即對于電網而言是恒功率負載。事實上電力作動器的大擾動狀態下運行，保證系統的穩定性更為重要，它不僅會影響對飛機舵面的操縱性能，而且更容易導致飛機電網的不穩定。改進型負阻抗補償器在航空電力作動器中的應用，不僅能夠保證作動器的動態性能，更為重要的是保證了電網的穩定性。

圖4給出了帶有改進型負阻抗補償器的航空作動器系統仿真及實驗曲線，系統參數如表1所示，伺服電機由啟動到平穩運行，0.25 s后到達給定偏角。圖4(a)左側為直流側電網電流，右側為電機轉速。控制電機在額定轉速下運行，在電機停車后仍需要一定的轉矩來維持偏角位置。實驗采用補償器設計方法，實驗曲線如圖4(b)所示。由于此時電源系統為開環理想電源和等效內阻結構組成，因此可通過電網電流波形來體現電網電壓響應。實驗數據表明該方法可大大改善電網電流波形，減小紋波大小，提高了系統穩定性，與理論推導結果一致。圖4可以看出，加補償后在電機啟動、運行及制動過程中，系統穩定，直流電網受影響程度較小，紋波系數小，可滿足航空供電要求，驗證了補償器對原系統穩定性及電能品質的改善。

圖4 帶有補償的航空作動器系統仿真及實驗曲線Fig.4 Simulations and experiments curves of the actuator system with compensator

4 結論

改進型負阻抗補償法從穩定性及系統性能兩方面考慮。其參數由不等式范圍決定，通過仿真分析可得，當高頻增益增大時，電網紋波減小，但過度增大會加大超調，且對電網擾動的抗干擾能力降低;當轉折頻率增大時，電機轉速超調量減小，調節時間縮短，但是電網電壓震蕩加劇，系統趨于不穩定。雖然公式推導自小信號法，但對于大擾動問題仍然適用。

通過仿真和實驗驗證，在同樣的紋波系數要求下，相對于大電容法，能更好的保障伺服電機平穩運行，從而實現使用較小電容滿足系統穩定性要求，同時滿足電機快速性及魯棒性。因此，帶有改進型負阻抗補償器的航空作動器系統以其簡單易行，線性等優勢具有較強的應用前景。

［1］ 劉欣博，周元鈞.具有雙級LC濾波器的恒功率負載系統在大擾動下的穩定性［J］.中國電機工程學報，2011，31(27):29-35.

LIU Xinbo，ZHOU Yuanjun.Large signal stability criteria for constant power loads with double-stage LC filters［J］.Proceedings of the CSEE，2011，31(27):29-35.

［2］ 朱成花，嚴仰光.Boost變換器恒功率負載時動態性能分析［J］.南京航空航天大學學報，2005，37(1):20-24.

ZHU Chenghua， YAN Yangguang. Stablity and dynamics of BOOST converter with constant power load［J］.Journal of Nanjing University of Aeronautics＆ Astronautics，2005，37(1):20-24.

［3］ JUSOH A B.The instability effect of constant power loads［C］//National Power and Energy Conference，Malaysia，2004.

［4］ 高朝暉，林輝，張曉斌.Boost變換器帶恒功率負載狀態反饋精確線性化與最優跟蹤控制技術研究［J］.中國電機工程學報，2007，27(13):70-75.

GAO Zhaohui，LIN Hui，ZHANG Xiaobin.Exact linearization and optimal tracking control of boost converter with constant power loads［J］.Proceedings of the CSEE，2007，27(13):70-75.

［5］ EMADI A，FAHIMI B，EHSANI M.On the concept of negative impedance instability in the more electric aircraft power systems with constant power loads［C］//34thIntersociety Energy Conversion Engineering Conference.Savannah，USA:ASME，1999:689-699.

［6］ EMADI A，KHALIGH A，RIVETTA C H，et al.Constant power loads and negative impedance instability in automotive systems:definition，modeling，stability，and control of power electronic converters and motor drives［J］.IEEE Transactions on Vehicular Technology，2006，55(4):1112-1125.

［7］ 錢浩，郭宏，呂振華.同步發電機整流系統帶恒功率負載的穩定性分析［J］.航空學報，2010，31(12):2379-2384.

QIAN Hao，GUO Hong，LV Zhenhua.Stability analysis of synchronous generator-rectifier systems with constant power loads［J］.Acta Aeronautica Et Astronautica Sinica，2010，31(12):2379-2384.

［8］ JELTSEMA D，SCHERPEN J M A.On Brayton and Moser’s missing stability theorem［J］.Circuits and Systems，2005，52(9):550-552.

［9］ Roux Nand Richardeau F.Stability of DC link with reduced energy storage for regenerative synchronous drive-Analytical approach［C］//European Conference on Power Electronics and Applications，2-5 Sept.2007，Aalborg，Denmark.2007:1-10.

［10］ MOSSKULL H，WAHLBERG B，GALIC J.Validation of stability for an induction machine drive using power iterations［C］//16th IFAC World Congress，Czech republic，2005.

［11］ ERICH S Y，POLIVKA W M.Input filter design criteria for current programmed regulators［J］.IEEE Transactions on Power E-lectronics，1992，7(1):143-151.

［12］ GIRINON S，PIQUET H，ROUX N，et al.Analytical input filter design in DC distributed power systems approach taking stability and quality criteria into account［C］//13th European Conference on Power Electronics and Applications，8-10 Sept.2009，Barcelona，Spain.2009:1-10.

［13］ MARX D，PIERFEDERICI S，DAVAT B.Nonlinear control of an inverter motor drive system with input filter-Large signal analysis of the DC-link voltage stability［C］//39thIEEE Annual Power Electronics Specialists，15-19 June，2008，Rhodes，Greece.2008:498-503.

［14］ 空軍 GJB181A-2003飛機供電特性［S］.2003.

［15］ CIEZKI J G，ASHTON R W.Application of feedback linearization techniques to the stabilization of DC-to-DC converters with constant power loads［C］//ISCAS，31 May-3 June 1998，Monterey，CA.1998:526-529.

［16］ LOOP B P，SUDHOFF S D，ZAK S H，et al.Estimating regions of asymptotic stability of power electronics systems using genetic algorithms［J］.IEEE Transactions on Control System and Technology，2010，18(5):1011-1022.

［17］ MOHEIMANI S O R.Perspectives in Robust Control(Lecture Notes in Control and Information Sciences)［M］.Berlin:Springer，2001.

［18］ HARNEFORS L，Pietl?inenardier K.Inverter DC-link stabilizing control with improved voltage sag ride-through capability［C］//European Conference on Power Electronics and Applications，2005，Dresden，Germany.2005:10 pp.-P.10.

［19］ LIU Xinyun，Andrew J，Andrew M.Negative input-resistance compensator for a constant power load［J］.IEEE Transactions on Industrial Electronics，2007，54(6).