基于支持向量機的開關磁阻電機轉子位置在線建模

司利云， 林輝

(1.長安大學 電子與控制工程學院，陜西西安710064;2.西北工業大學 自動化學院，陜西 西安710072)

0 引言

開關磁阻電機驅動系統(switched reluctance motor drive system，SRD)以其結構簡單、工作可靠、效率高和成本較低等優勢，成為工業應用中比較理想的電機選擇，最近其作為最有可能進入電動汽車和混合電動車輛市場的主流產品而備受關注［1］。SRD是位置閉環系統，獲取轉子位置信號的傳統方式是采用機械式位置傳感器直接檢測。位置傳感器的存在削弱了SRD結構簡單的優勢，降低了系統高速運行的可靠性。因此，探索取消位置傳感器的轉子位置間接檢測方法成為SRD研究的一個熱點。

近年來許多學者都對該問題進行了探討，提出了各種可行的方案［2］。這些方案大都利用了電機可測的電氣參數與轉子位置之間存在的函數關系，基于這種函數關系解算出轉子位置信息，其中最有代表性的便是使用如模糊邏輯［3］、神經網絡［4－5］或支持向量機［6－7］等人工智能法間接獲取轉子位置信號，但是這些方法大都使用離線獲取的磁化特性曲線進行學習，所建立的離線模型在實際工程應用中，由于電機的運行狀態會出現不規律的變化，并且存在各種干擾因素，使得所建立的離線模型無法滿足電機的工程應用要求［8］。基于此，為了使所建立的轉子位置估計器模型能夠更加準確地描述電機的運行狀態，目前有兩種解決思路，一種是設計模型的在線調節方法，對離線模型進行在線學習和調節。如文獻［8］首先利用基于徑向基函數的神經網絡建立開關磁阻電機的離線模型，然后在電機實際運行過程中，根據估計磁鏈和實際磁鏈的誤差，實時地調整神經網絡的輸出權值，使得經過在線調整的磁鏈模型更加準確地描述電機的磁鏈特性;另一種則是直接使用在線建模技術對轉子位置進行實時預測。如文獻［5］建立了轉子位置檢測的神經網絡模型，并給出了模型的在線學習算法和訓練步驟，采用TMS320F2812 DSP實現神經網絡在線訓練算法，開發完成了一臺15 kW三相12/8極無位置傳感器SRD樣機。實驗結果表明，無位置傳感器SRD具有較好的動態特性和較高精確度。本文將從在線建模的角度出發，將只受極少數的相關數據點(支持向量)的影響，且計算量較小的支持向量機模型作為研究的重點，研究利用開關磁阻電機實際運行過程中獲取的磁特性數據建立轉子位置估計器的在線預測模型。

1 支持向量機在線建模原理

系統實際運行過程中得到的數據集會隨著時間的推移及工作區域的變化而動態改變，從而使得建立的在線模型也是動態變化的。

假設系統當前的狀態主要由過去時刻到當前時刻的l組數據來描述，這個區域段的樣本集為{(x1，y1)，(x2，y2)，…，(xl，yl)}∈Rn× R，當前系統的建模信息便從這l組數據中得到。隨著系統的運行，系統狀態的不斷改變，新的數據不斷得到，要使模型能準確的反映系統的當前狀態，就要用新的數據集來描述模型。通常使用的建模過程如下［9］:

1)選擇適當的支持向量回歸機模型;

2)以{(x1，y1)，(x2，y2)，…，(xl，yl)}∈Rn× R為訓練樣本集建立系統模型;

5)若誤差在允許的范圍之內，則l←l+1轉3);

6)否則便轉2)，將采集的數據加到訓練樣本集中，在新的數據集上重新建立模型。

有別于離線建模對支持向量回歸機模型的要求，在線建模除了希望模型具有良好的逼近精確度，還希望模型的訓練算法具有較快的收斂速度，以便滿足在線建模對實時性的需求。

目前在線建模使用最多的模型可分為兩類:一類以標準支持向量回歸機模型(standard support vector regression，SSVR)為代表［10－12］;另一類以最小二乘支持向量回歸機模型(least squares support vector regression，LSSVR)為代表［13－15］。前者由于要求解二次規劃問題，所以需要的訓練算法比較復雜;后者只需求解一組線性方程組，算法簡單快速，但其解卻喪失了稀疏性。為了尋求一種適合電機實際運行特性的在線建模算法，本文將探討基于灰色關聯的加權分類近似支持向量回歸機模型來進行轉子位置估計器的在線建模。

2 基于灰色關聯的加權分類近似支持向量回歸機模型

2.1 分類近似支持向量回歸機模型

近似支持向量機(proximal support vector machine，PSVM)是由 Fung和 Mangasaran提出的一種解決分類問題的變形支持向量機［16］。其通過將標準支持向量機的損失函數由一次改為二次，并在目標函數中加入偏移項b2，使目標函數成為強凸函數，算法的收斂速度比標準支持向量機要快得多;另外其將約束條件由不等式約束變為等式約束，不需要求解二次優化問題，大大降低了求解的難度。本文又借鑒了文獻［17］提出的分類支持向量機的思想，通過樣本集因變量的上下平移將回歸問題轉化為二值分類問題，將近似支持向量機的分類算法推廣到回歸問題中，得到了分類近似支持向量回歸機模型(proximal support vector regression via classification，CPSVR)，其對應的優化問題為

式中:(w，η)為超平面的權向量;b為偏置;非線性映射φ(·)將輸入空間的樣本點映射到一個高維的特征空間(Hilbert空間);＜·＞表示向量內積;ξj為松弛變量(也是回歸誤差項);C為懲罰因子;ε為容許誤差;zj為類別標簽，取值為+1或－1。

利用對偶理論得到對應的線性方程組為

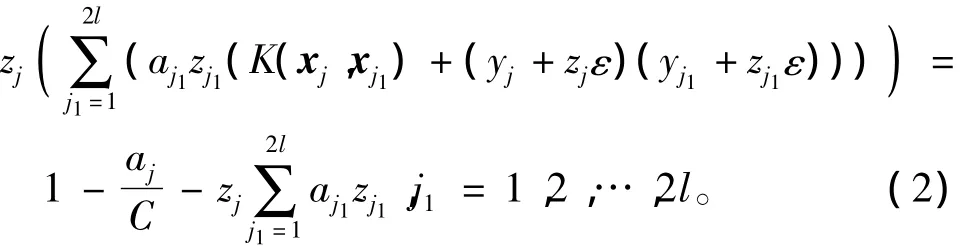
式中:aj1和 aj為 Lagrange乘子;K(xj，xj1)為核函數，K(xj，xj1)=〈φ(xj)·φ(xj1)〉，其中 xj，xj1為訓練樣本集中的任意兩個樣本。

求解上述方程組，得到CPSVR對應的非線性回歸函數為

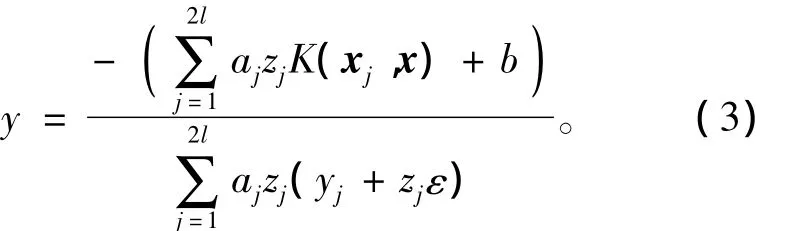
式中核函數K(xj，x)中xj為訓練后得到的支持向量樣本，因為該模型的解喪失了稀疏性，所以訓練樣本便全部成為支持向量;x為測試集中的樣本。

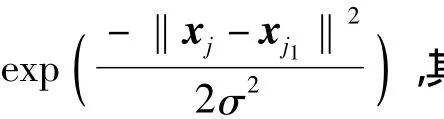
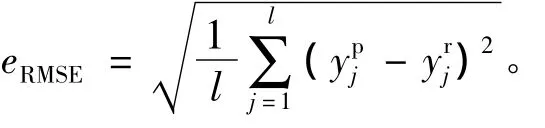
測試結果如表1所示。

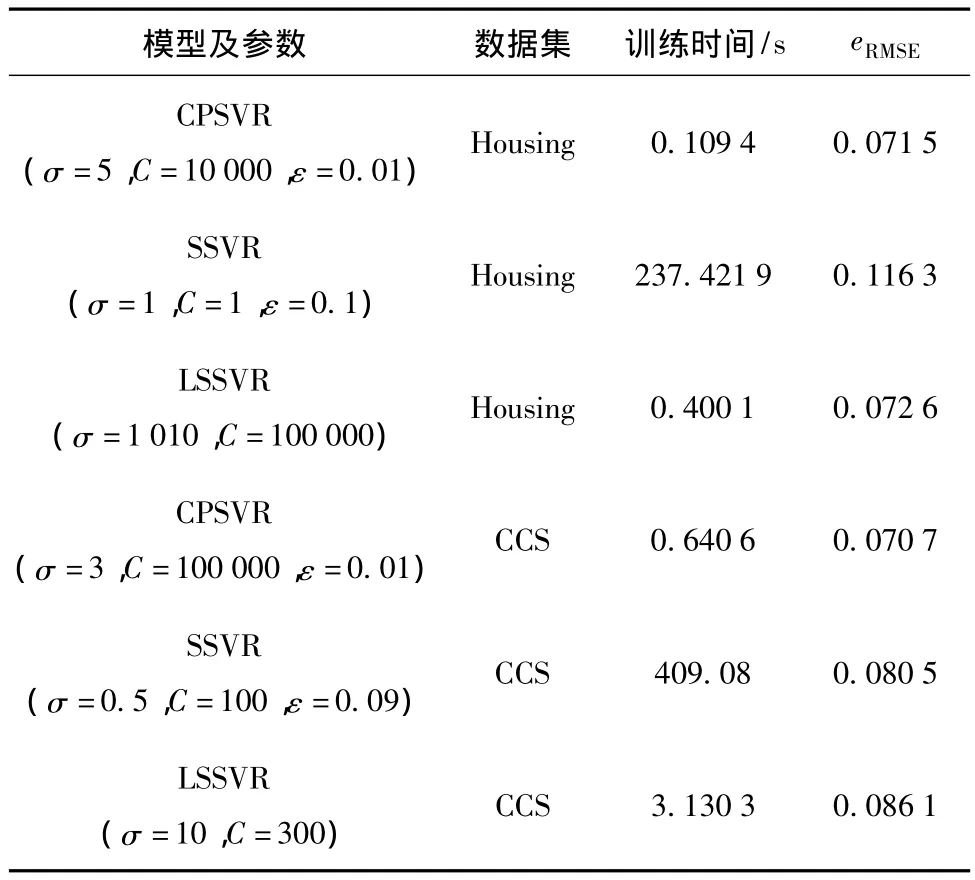
表1 模型在標準數據集上的測試結果Table 1 Model test results on the standard data set

從表1中可以看出，CPSVR與SSVR和LSSVR相比，所需的訓練時間短，預測精確度高。雖然其解與LSSVR一樣都不具備稀疏性，但預測精確度上有了較大的提高;所以從預測精確度與收斂速度兩方面考慮，CPSVR用于在線建模是不錯的選擇。

2.2 基于滾動時間窗的加權分類近似支持向量回歸機

上述模型由于只需求解線性方程組，所以計算簡單快速，但由于其解不具備稀疏性，不存在支持向量，如果直接用于在線建模，隨著時間的推移，可能會導致訓練樣本集的無限擴大，引入較多的冗余信息，所以借鑒文獻［12］提出的加權滾動時間窗的做法，固定訓練樣本集合的大小，構造滾動時間窗獲取動態建模所需的數據集，并對滾動時間窗內的數據分配不同的權值h以反映樣本對模型的重要程度，這樣便可使模型隨著時間窗的滾動在線更新，數據容量不會隨著時間的推移而過分增大。

基于上述思想，本文對分類近似支持向量回歸機模型進行了修正，采用給誤差項ξj增加權值hj(h1，…，hj，…，hN分別對應時間窗內的 N 個樣本的權值)的方法來決定區間中N個樣本的重要性。由此得到加權分類近似支持向量回歸機模型(weighted proximal support vector regression machine via classification，WCPSVR)。

給定從t時刻開始的N區間內的樣本數據集{(x1，y1)，(x2，y2)，…，(xl，yl)}∈Rn× R，WCPS-VR對應的優化問題為

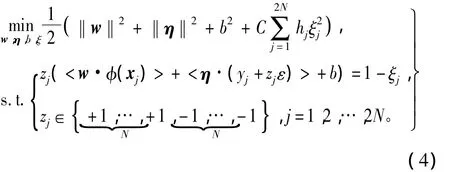
利用對偶理論得到如下的線性方程組，即

求解上述方程組，得到WCPSVR對應的非線性回歸函數為

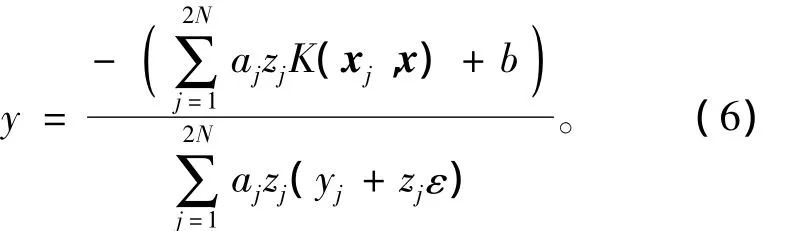
2.3 基于灰色關聯的權值選取方法

對于時間窗內訓練樣本的權值選取通常是根據采樣時刻的遠近來決定權值的大小，認為采樣時刻越遠的樣本與預測樣本的相關性越小，在預測模型中所占比重越小，而采樣時刻越近的樣本越重要，在模型中所占的比重越大，可用下面的加權函數［12］來實現，即

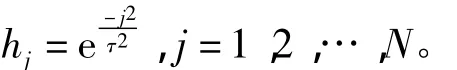
其中，τ為人為給定的參數，小的τ值可減少歷史數據的存儲，加快訓練速度。

從開關磁阻電機的運行方式來看，這種權值選取方法并不是非常合適，因為電機運行時，相電流與相磁鏈呈周期性變化，電流的上升沿與下降沿比較陡峭，假設當前的預測樣本比較接近波谷，從時間上看離該預測樣本較近的應是同一個波的波頂數據，而前一個波的波谷數據則由于采樣時刻較遠而得不到重視，但從電機運行方式來看，應該是物理特性比較相近的數據對預測結果更有意義，因為這些樣本可能具有極為相近的相電流、相磁鏈及轉子位置角，所以對波谷樣本的預測而言，時間上距離較遠的波谷數據應給以更大的權重。基于此，本文將使用灰色關聯度來決定權值。

灰色關聯分析［18］是研究系統中多個因素之間相互作用、相互關聯的一種統計方法，當系統內存在復雜的相互影響，在其效果、結構、整體性能、優劣度、權重等方面所吸收與采用的信息不明確、不完整時，它是一種有力的定量分析工具。在某些方面與支持向量機方法有著相同的前提，如都是針對信息殘缺或貧乏的系統，所以在支持向量機的貧信息背景下引用灰色系統的理論與方法，理論上是可行的。

設系統的特征序列(參考序列)為V0={v0(1)，v0(2)，…，v0(n)}，相關因素序列(比較序列)為Vj={vj(1)，vj(2)，…，vj(n)}，其中 j=1，2，…，m。灰關聯系數γ(v0(k)，vj(k))定義為

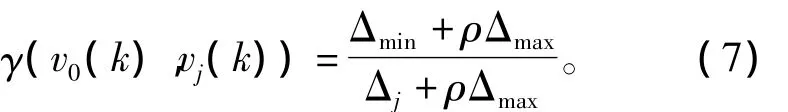
那么序列V0與Vj灰關聯度γ(V0，Vj)為

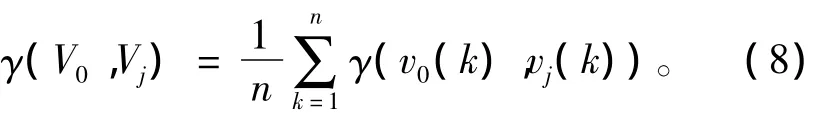
灰關聯空間(V，Γ)是距離空間與點集拓撲空間的融合，其中V表示灰關聯因素序列集，Γ是灰關聯映射集。在上式中，|v0(k)－vj(k)|是距離測度，Δmin與Δmax是vj(k)與v0(k)的比較環境，也是vj(k)的領域，包含了點集拓撲的信息，ρ的作用在于調節比較環境的強弱。

灰關聯度便是所尋求的預測樣本(參考序列)與滾動時間窗內的訓練樣本(比較序列)之間的權值關系hj，其通過反映樣本之間在空間距離上存在的相互關系，強調了樣本的物理相似性。

3 基于灰色關聯的WCPSVR在線轉子位置預測模型的性能測試

3.1 在線轉子位置預測模型的建立

獲取電機運行過程中某一時刻的相電壓Uj、相電流ij及轉子位置信息θj，由式(9)計算對應的相磁鏈值 ψj，即

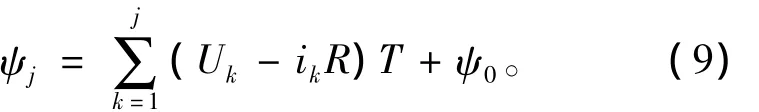
式中:R為相繞組的電阻;j=1，2，…，N;T為采樣周期;N為測量點個數。若已知從時刻0到時刻TN內每個采樣點的電壓Uk和電流ik以及時刻0的初始磁鏈ψ0，便可得到當前時刻的磁鏈ψj。

以電流 ij及磁鏈 ψj作為自變量 xj，θj為因變量，WCPSVR作為支持向量回歸機模型，按以下步驟建立在線轉子位置預測器。

1)取N區間測量數據組成訓練樣本集{(x1，θ1)，…(xj，θj)，…，(xN，θN)}∈R2× R，用歸一化處理方法對數據進行校正與預處理;

2)設定初始參數值。核函數采用徑向基函數，σ=0.1，容許誤差ε取為θ的線性函數ε=0.008θ，C=1 000;分辨系數ρ=0.75;對WCPSVR進行訓練，建立轉子位置θ的預測模型;

4)若誤差在允許的范圍之內，則l←l+1轉3);

5)否則便轉1)，讓采集的樣本進入滾動時間窗內，時間窗進行滾動，丟棄權值最小的樣本，并重新建立轉子位置估計器模型。

3.2 模型的測試結果及性能分析

以一臺3 kW 12/8極的開關磁阻電機為研究對象，其額定輸入電壓為三相交流電380 V/50 Hz，額定轉速為1 500 r/min，調速范圍為100～2 000 r/min，功率變換器主電路采用不對稱半橋線路，控制方式選為電壓PWM控制加電流斬波控制，導通角為0°到 15°。

獲取電機不同運行工況下的相電流、相磁鏈及轉子位置信息，其中，相電流信號通過電流傳感器獲取，轉子位置信號通過機械位置傳感器獲取，建立在線轉子位置預測模型，即

圖1為負載1 N·m情況下轉速為1 500 r/min時在線轉子位置預測模型的測試結果。經過實驗測試發現，當訓練樣本集(×代表訓練樣本點)的固定長度N=40，能夠覆蓋相電流(圖1(a))與相磁鏈(圖1(b))的上升段后，便可對隨后采集的預測樣本獲得較高的預測精確度(圖1(c))，最大絕對誤差值為 2.194 5°，平均絕對誤差值為 0.115 9°;圖1(d)給出了實測的轉子位置角及對應的較大預測誤差值的分布情況，可以看出，在換相位置附近，由于相電流與相磁鏈的波動比較劇烈，模型的預測精確度會比較低。

圖1 負載1 N·m轉速1 500 r/min時模型的測試結果Fig.1 Model test results under load 1 N·m and speed 1 500 r/min

圖2為負載10 N·m情況下轉速為800 r/min時在線轉子位置預測模型的測試結果，當訓練樣本集(×代表訓練樣本點)的長度N=48，可以覆蓋相電流(圖2(a))與相磁鏈(圖2(b))的上升段后，便可獲取比較滿意的預測精確度。這表明轉子位置估計器模型具有良好的泛化能力。圖2(c)給出了預測樣本的誤差曲線，其中最大絕對誤差值為2.616 3°，平均絕對誤差值為0.311°;圖2(d)給出了較大的預測誤差值對應的轉子位置角的分布情況，同負載1 N·m情況下相似，在換相位置附近，即在0°與15°附近，模型的預測精確度較低。主要原因是由于這個階段數據波動比較劇烈，固定長度的訓練樣本集不可能很好的體現這個階段的數據特征，從而不能獲取較好的預測效果。

圖2 負載10 N·m轉速800 r/min時模型的測試結果Fig.2 Model test results under load 10 N·m and speed 800 r/min

4 結語

針對開關磁阻電機離線轉子位置估計器在實際工程應用中存在的預測精確度較差、甚至在某些情況下失效的不足，本文研究了在線轉子位置預測技術。這種技術需要充分考慮電機的實際運行情況，并根據其運行方式及特點，建立快速的且高精確度的轉子位置估計器模型。基于上述前提，本文提出了基于灰色關聯的加權分類近似支持向量回歸機。在標準數據集上的測試結果表明該模型具有較快的收斂速度與較高的預測精確度。基于灰色關聯度的在線滾動時間窗內訓練樣本的選取方法，由于考慮了樣本間的空間與時間關系，使得只需很小的訓練樣本數目，便可實現位置的準確估計，這也表明了該模型具有良好的泛化能力。

但是由于在線建模方法的訓練樣本集需要真實準確的轉子位置信息，在模型性能驗證的初期，可以使用機械位置傳感器來提供這個信號，驗證模型的預測精確度。但在后面的在線建模方法實用化過程研究中，這種位置信號的獲取方法無疑是不可行的，那么，用什么方法獲取在線建模所需要的能夠替代真實的精確轉子位置信號，這將是在線建模所必須解決的一個問題及后續工作的重點。

［1］ 王宏華.開關型磁阻電動機調速控制技術［M］.北京:機械工業出版社，1995:1－50.

［2］ 鄧智泉，蔡駿.開關磁阻電機無位置傳感器技術的研究現狀和發展趨勢［J］.南京航空航天大學學報，2012，44(5):611－620.

DENG Zhiquan，CAI Jun.Research Status and development trends of sensorless techniques of switched resultance motor［J］.Journal of Nanjing University of Aeronautics＆ Astronautics，2012，44(5):611－620.

［3］ CHEOK A D，ERTUGRUL N.High robustness and reliability of fuzzy logic based position estimation for sensorless swtiched reluctance motor drives［J］.IEEE Transactions on Power Electronics，2000，15(2):319－334.

［4］ 張旭隆，譚國俊，蒯松巖，等.磁鏈模型的雙開關磁阻電機無位置傳感器控制［J］.電機與控制學報，2011，15(11):55－60.

ZHANG Xulong，TAN Guojun，KUAI Songyan，et al.Sensorless control of double switched reluctance motor based on flux model［J］.Electric Machines and Control，2011，15(11):55 －60.

［5］ 蒯松巖，張旭隆，王其虎，等.開關磁阻電機神經網絡無位置傳感器控制［J］.電機與控制學報，2011，15(8):18－22.

KUAI Songyan，ZHANG Xulong，WANG Qihu，et al.Position sensorless control of SRM using neural network［J］.Electric Machines and Control，2011，15(8):18 －22.

［6］ 朱志瑩，孫玉坤，嵇小輔，等.磁懸浮開關磁阻電機轉子位移/位置觀測器設計［J］.中國電機工程學報，2012，32(12):83－89.

ZHU Zhiying，SUN Yukun，JI Xiaofu，et al.Displacement and position observers designing for bearingless swtiched reluctance motor［J］.Proceeding of the CSEE，2012，32(12):83 －89.

［7］ 夏長亮，賀子鳴，周亞娜，等.基于支持向量機的開關磁阻電機轉子位置估計［J］.電工技術學報，2007，22(10):12－17.

XIA Changliang，HE Ziming，ZHOU Yana，et al.Rotor position estimation for switched reluctance motors based on support vector machine［J］.Transactions of China Electrotechnical Society，2007，22(10):12－17.

［8］ 蔡永紅，齊瑞云，蔡駿，等.基于RBF神經網絡的開關磁阻電機在線建模及其實驗驗證［J］.航空學報，2012，33(4):705－714.

CAI Yonghong，QI Riyun，CAI Jun，et al.Online modeling for switched reluctance motor using radial basic function neural network and its experimental validation［J］.Acta Aeronautica et Astronautica Sinica，2012，33(4):705 －714.

［9］ 王定成，方廷健，高理富，等.支持向量回歸機在線建模及應用［J］.控制與決策，2003，18(1):89－95.

WANG Dingcheng，FANG Tingjian，GAO Lifu，et al.Support vector machines regression on-line modelling and its application［J］.Control and Decision，2003，1 8(1):89 －95.

［10］ 閻威武，常俊林，邵惠鶴.基于滾動時間窗的最小二乘支持向量機回歸估計方法及仿真［J］.上海交通大學學報，2004，38(4):524－532.

YAN Weiwu，CHANG Junlin，SHAO Huihe.Least square SVM regression method based on sliding time window and its simulation［J］.Journal of Shanghai Jiaotong University，2004，38(4):524－532.

［11］ MA J S，THEILER J，PERKINS S.Accurate on-line support vector regression［J］.Neural Computation，2003(15):2683－2703.

［12］ 汪輝，皮道映，孫優賢.支持向量機在線算法及其應用［J］.浙江大學學報:工學版，2004，38(12):1642－1645.

WANG Hui，PI Daoying，SUN Youxian.On-line support vector machine training algorithm and its application［J］.Journal of Zhejiang University:Engineering Science，2004，38(12):1642－1645.

［13］ 鄭小霞，錢鋒.基于支持向量機的在線建模方法及應用［J］.信息與控制，2005，34(5):636－670.

ZHENG Xiaoxia，QIAN Feng.An SVM-based on-line modeling method and its application［J］.Information and Control，2005，34(5):636－670.

［14］ YAAKOV E，SHIE M，RON M.Sparse online greedy support vector regression［C］//Proceeding of the 13th European Conference on Machine Learning，August 19 － 23，2002，London，UK.2002:84－96.

［15］ VIJAYAKUMAR S，WU S.Sequential support vector classifiers and regression［C］//Proceedings of the International Conference on Soft Computing，June 1 －4，1999，Genoa，Italy.1999:610 －619.

［16］ FUNG G，MANGASARIAN O L.Proximal support vector machine classifiers［C］//Proceedings of the Seventh ACM SIGKDD International Conference on Knowledge Discovery and Data Mining，August 26 － 29，2001，San Francisco，USA.2001:77－86.

［17］ BI J，BENNETT K P.A geometric approach to support vector regression［J］.Neurocomputing，2003，(55):79 －108.

［18］ 劉思峰.灰色系統理論及其應用［M］.北京:科學出版社，2010:49－58.