帶過濾機制非線性慣性權(quán)重粒子群算法

秦毅，彭力

江南大學(xué)物聯(lián)網(wǎng)工程學(xué)院，江蘇無錫 214122

帶過濾機制非線性慣性權(quán)重粒子群算法

秦毅，彭力

江南大學(xué)物聯(lián)網(wǎng)工程學(xué)院，江蘇無錫 214122

為改進非線性慣性權(quán)重粒子群算法，提出了一種帶過濾機制的非線性慣性權(quán)重粒子群算法。由于原算法存在粒子易陷入局部最優(yōu)解與搜索效率較低的缺點，將適應(yīng)度縮放函數(shù)引入到非線性慣性動態(tài)調(diào)整的粒子群算法中，剔除適應(yīng)度過高與過低的粒子，再對剩余種群部分優(yōu)良個體進行復(fù)制，并隨機產(chǎn)生一些新粒子，然后進行交叉操作，種群數(shù)量保持不變，減少了粒子陷入局部極值的概率，使結(jié)果收斂于全局最優(yōu)解。通過低維度與高維度函數(shù)的對比測試，表明新算法具有較為理想的效果。

過濾機制；適應(yīng)度縮放；慣性權(quán)重；非線性粒子群算法

1 引言

很多學(xué)者針對標(biāo)準(zhǔn)粒子群算法易陷于早熟收斂，局部最優(yōu)，提出了改進的粒子群算法[1-5]。針對其收斂速度的情況，有學(xué)者提出了慣性權(quán)重遞增的算法[6]，也有學(xué)者提出了慣性權(quán)重遞減的方法[7]，這些算法在一定程度上都改善了算法的收斂速度及算法得到最優(yōu)解的特性。通過實驗發(fā)現(xiàn)，具有遞增慣性權(quán)重的粒子群算法前期收斂速度較快，但是容易陷入局部最優(yōu)解，具有遞減慣性權(quán)重的粒子群算法前期具有較強的局部搜索能力，但是后期收斂速度較差。

本文提出了一種帶過濾機制的交叉粒子非線性慣性權(quán)重動態(tài)調(diào)整的PSO算法，首先對位置和速度進行非線性自適應(yīng)調(diào)整，然后通過適應(yīng)度縮放函數(shù)將適應(yīng)度很好以及很不好的粒子剔除，再對進化過程中部分不良適應(yīng)值的粒子用優(yōu)良的粒子進行復(fù)制交叉，減少不良適應(yīng)值粒子出現(xiàn)的概率，從而使得算法在初期就過濾掉了一些不良粒子，加快了算法的收斂速度，減小了粒子陷于早熟收斂的概率，更加快速地得到最優(yōu)解。

2 算法模型

粒子群優(yōu)化算法（PSO）和其他進化類算法類似，是一種迭代的優(yōu)化算法。PSO算法最初是Kennedy博士和Eberhart教授于1995年提出的，該算法模仿鳥群等群體動物尋找食物的社會性行為來建立的，具有算法簡單及容易實現(xiàn)的優(yōu)點[8]。在PSO算法中，每個粒子都代表著搜索空間中的一個可行解，所有粒子都有一個由被優(yōu)化的函數(shù)決定的適應(yīng)值，粒子的速度和位置決定了它飛翔的距離和方向，粒子通過跟蹤兩個極值來更新自己，一個是粒子本身所經(jīng)歷的最優(yōu)解，稱為個體極值Pi；另一個極值是整個種群目前找到的最優(yōu)解，稱為全局極值Pj。假設(shè)在一個m維搜索空間中，有n個粒子組成一粒子群，其中第i個粒子的空間位置為Xi=(Xi1，Xi2，…，Xim)其飛行速度Vi=(Vi1，Vi2，…，Vim)，i=1，2，…，n。Xi是優(yōu)化問題的一個潛在解，將它代入優(yōu)化目標(biāo)函數(shù)可以計算出相應(yīng)的適應(yīng)值，根據(jù)適應(yīng)值可衡量Xi的優(yōu)劣。對每一代粒子，其速度及位置的更新公式如下：

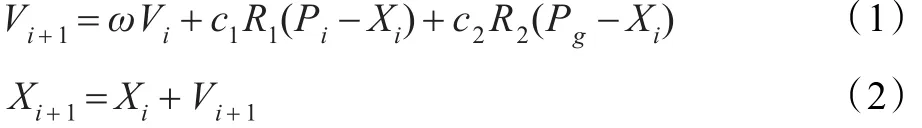
其中，ω為慣性權(quán)值，它使粒子保持運動慣性。c1和c2都為正常數(shù)，稱為加速系；R1和R2是兩個在[0，1]范圍內(nèi)變化的隨機數(shù)，用以保證粒子群體的多樣性和搜索的隨機性。

Vi+1是Vi、Pj-Xi和Pg-Xi的矢量和，如圖1所示。粒子速度的每一維都會被限制在一個最大速度Vmax(Vmax＞0)，若某一維更新后的速度超過用戶設(shè)定的Vmax。

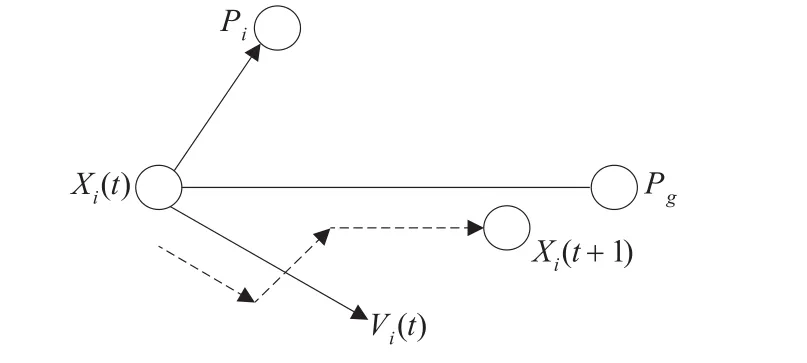
圖1 粒子可能移動方向圖

為了保證粒子在優(yōu)化前期的快速性，以及保證粒子在優(yōu)化后期不發(fā)散，對標(biāo)準(zhǔn)粒子群算法的公式進行調(diào)整，加入一個自適應(yīng)參數(shù)來保證上述要求。

3 穩(wěn)定性分析

為方便推導(dǎo)，現(xiàn)將式（1）和（2）簡記成式（4）和（5），其中C1=c1r1，C2=c2r2，Pg，Pb為外部輸入[9]。

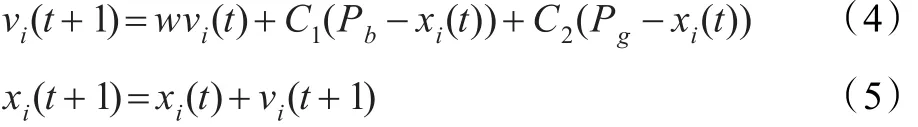
把式（4）和（5）中的時間項向后推一步，得：

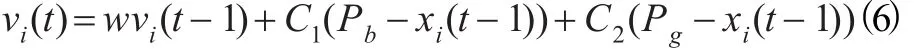
假設(shè)Pg和Pb在粒子運動過程中保持不變，由式（4）、（5）、（6）和（7）得：

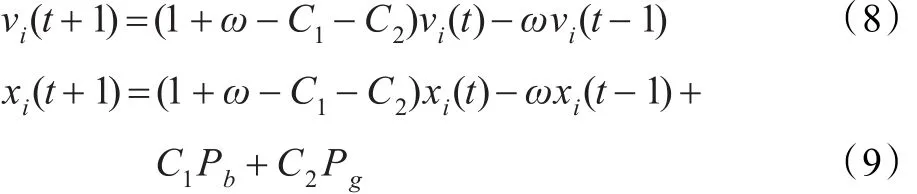
若將粒子的速度變化過程看作一個時間連續(xù)過程，則式（9）可對應(yīng)一個典型的二階齊次線性微分方程：

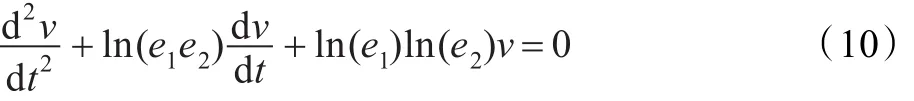
其中e1，e2為方程（*）的根。

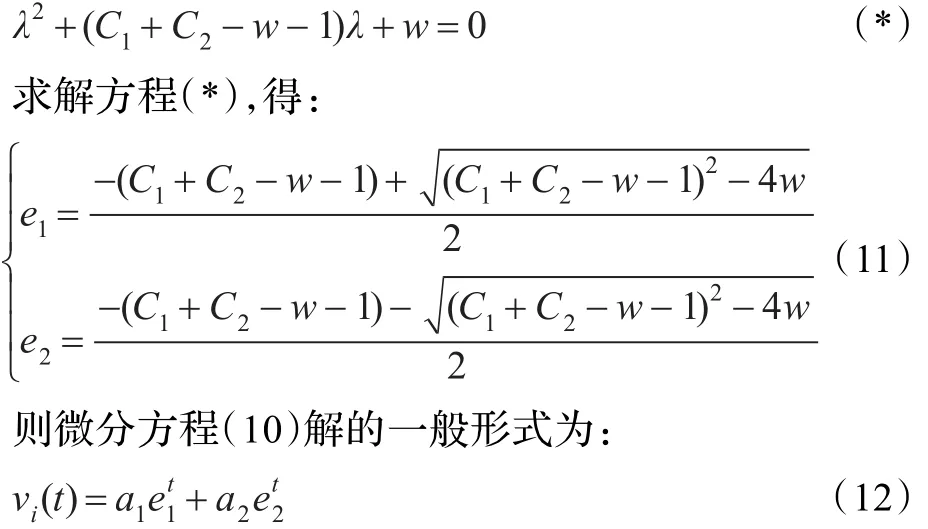
如果將位置變化看作一個時間連續(xù)過程，則式（12）可對應(yīng)一個二階微分方程，其對應(yīng)的一般解的形式為：

其中k1，k2，k3是與粒子初始狀態(tài)相關(guān)的常數(shù)，記粒子第0、1、2步的位置為xi(0)，xi(1)，xi(2)，由式（13）有

當(dāng)粒子位置趨向無窮大時，粒子的運動軌跡將是發(fā)散的，多個粒子運動軌跡發(fā)散也將導(dǎo)致粒子群的發(fā)散。下面對粒子位置變化過程的穩(wěn)定性進行分析。

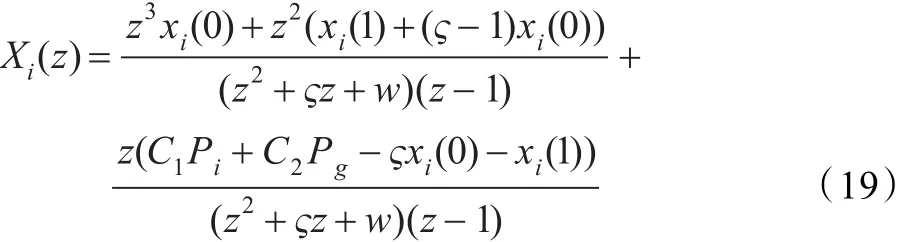
對式（14）取Z變換，得：其中，?=C1+C2-1-w。為便于分析，假設(shè)C1，C2為某一常數(shù)使得式（19）成為一個線性系統(tǒng)，其特征方程為：

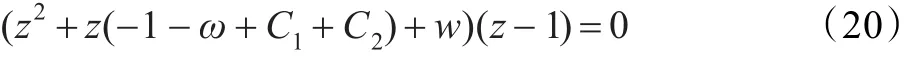
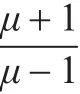
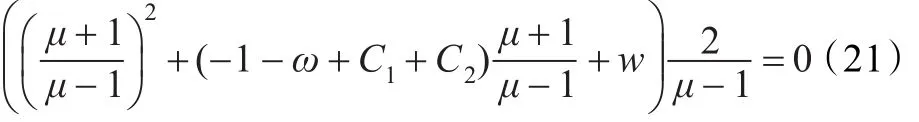
整理后得：

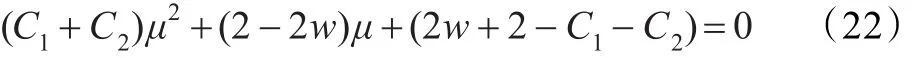
粒子的位置變化過程穩(wěn)定的條件為：

當(dāng)滿足條件式（24）時，由Z變換的終值定理可得：

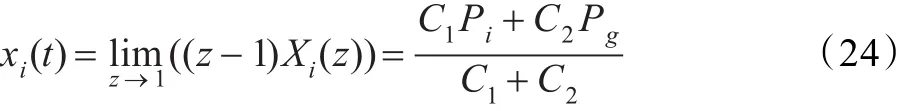
4 算法改進

本文提出了一種帶過濾機制的粒子交叉復(fù)制與慣性權(quán)重相結(jié)合、慣性權(quán)重沿正弦曲線先增后減的改進粒子群算法，并且對速度進行參數(shù)自適應(yīng)調(diào)整，這樣算法在保證前期階段具有較快的收斂速度的同時，對種群進行過濾，減小了不良粒子出現(xiàn)的概率。算法首先計算出種群中每一個粒子所對應(yīng)的適應(yīng)值，剔除適應(yīng)值不良的部分個體，再從剩余的個體中選出一些適應(yīng)值優(yōu)良的個體，使這些個體在種群中復(fù)制一次，另外隨機產(chǎn)生一新個體，這兩個群體之間在進行交叉，復(fù)制及新產(chǎn)生的個體數(shù)量之和等于過濾掉粒子的數(shù)量，以保持種群大小不變。這樣優(yōu)良適應(yīng)值的粒子取代部分適應(yīng)值不良的個體，使得優(yōu)秀適應(yīng)值個體在種群中所占比例增大。保證收斂速度的同時避免搜索過程中過早地陷于局部最優(yōu)解，適當(dāng)補充新個體，增強種群活力，提高搜索到最優(yōu)解的可能性。這樣既保留了原來算法收斂速度快，又克服了原算法易陷入局部最優(yōu)解的缺點，取得了比較好的實驗效果。

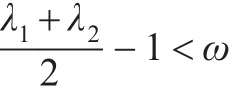
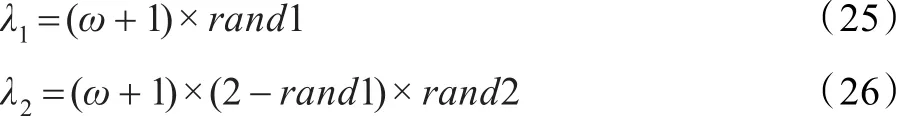
對ω，η參數(shù)進行自適應(yīng)動態(tài)調(diào)整。參數(shù)的調(diào)整規(guī)律[10]為：

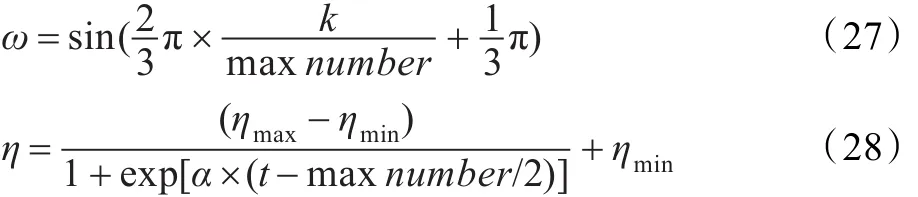
式（25）中，ηmax，ηmin是η變化的最大值與最小值，一般取ηmax∈[1.0，1.8]，ηmin∈[0.4，0.8]，t為粒子群進化代數(shù)，maxnumber為最大迭代次數(shù)，一半取α∈[0.005，0.015]。

5 仿真研究

為了驗證上文中提出算法的性能，采用Shaffer’sF6、LevyNo.5、4Generalized Schwefel’s Problem 2.26、以及Generalized Griewank Function四個函數(shù)，對其加以測試，并對結(jié)果進行分析。函數(shù)特性如表1所示。

表1 函數(shù)特性表

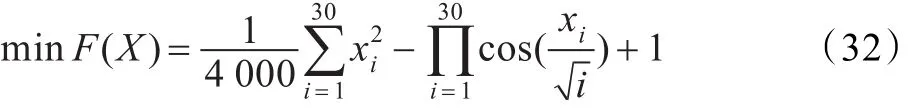
上述函數(shù)中，前兩個是二維的函數(shù)，后兩個是多維的函數(shù)，分別用以上四個函數(shù)做測試，測試過程中，種群數(shù)設(shè)置為50，最大迭代數(shù)為2 000，迭代結(jié)束的條件為最優(yōu)解與最優(yōu)適應(yīng)值差小于0.000 01。仿真實驗共做3次，每次實驗中共進行100次優(yōu)化過程。陷入局部極值的實驗結(jié)果如表1。

表2中1表示本文提出的例子群算法，2表示基本粒子群算法，3表示非線性慣性權(quán)重的粒子群算法。從表2中可以看出，采用本文提出的PSO算法，能有效地避免粒子陷入局部最優(yōu)解，同時還能保證算法的快速性。算法的性能優(yōu)于其他的兩種。

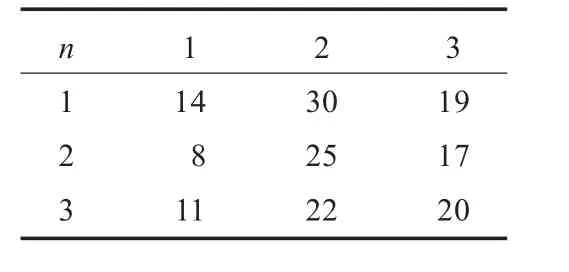
表2 三種方法的陷入局部極值次數(shù)對比

為了更進一步地表現(xiàn)本文提出的算法的有效性，用基本粒子群算法，非線性慣性權(quán)重粒子群算法，以及本文提出的改進算法對上文中提出的四個測試函數(shù)進行優(yōu)化，對結(jié)果做了對比，對比圖形如圖2～圖5所示。

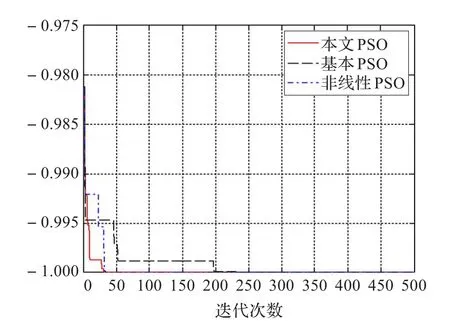
圖2 Shaffer’s F6函數(shù)的對比測試圖

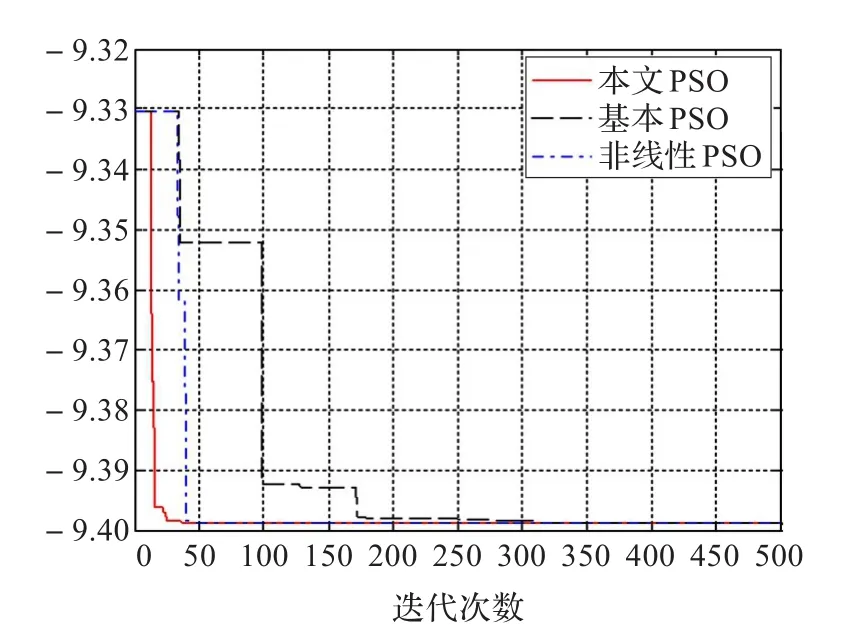
圖3 LevyNo.5函數(shù)的對比測試圖

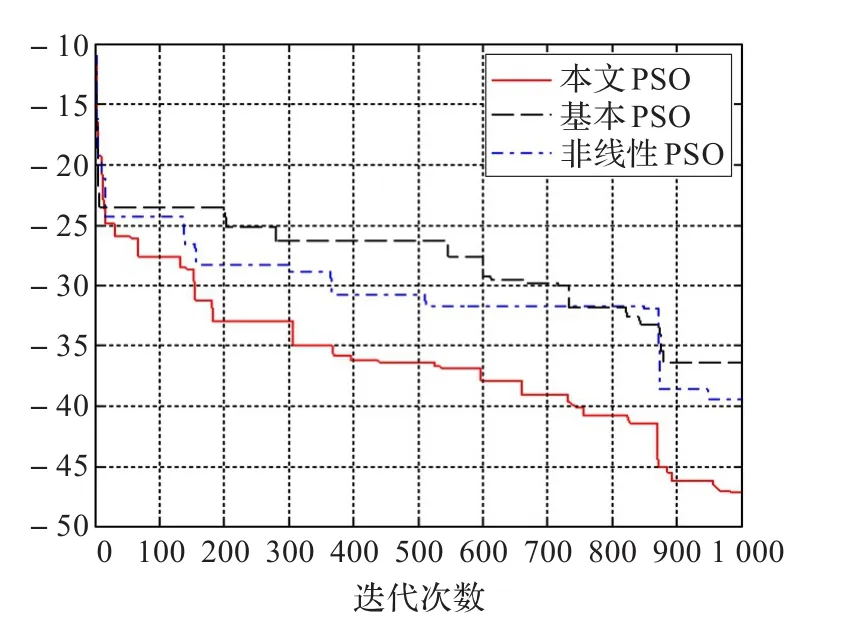
圖4 Generalized Schwefel’s Problem 2.26函數(shù)的對比測試圖

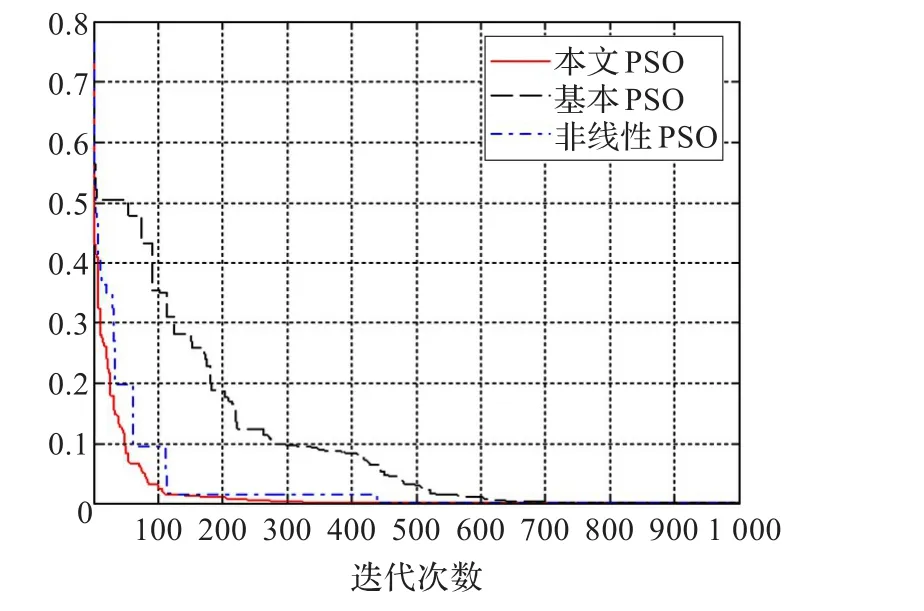
圖5 Generalized Griewank Function：函數(shù)的對比測試圖

從圖2～圖5可以看出，在算法的初期，本文提出的算法在保證了收斂速度的同時，也避免了算法陷入局部最優(yōu)解，而在算法的后期收斂速度有所降低，能夠保證尋優(yōu)的過程能逐漸接近最優(yōu)解，避免了粒子震蕩的發(fā)生。而對于維度較低的測試函數(shù)，本文改進的粒子群算法相對于其他兩種算法的優(yōu)勢不是特別明顯，而對于高維度的函數(shù)，即圖4、5可以看出，本文改進的算法在保證收斂速度的同時也很好地克服了算法在尋優(yōu)的過程中陷入早熟收斂。

6 結(jié)論

本文提出了一種帶過濾機制的交叉粒子非線性慣性權(quán)重動態(tài)調(diào)整的PSO算法在保證了算法前期的搜索速度的同時，避免了粒子陷入局部最優(yōu)解，而在算法的后期，避免了無效粒子過多而出現(xiàn)粒子震蕩，對于高維度的函數(shù)來說，本文提出的算法在尋優(yōu)過程中明顯優(yōu)于其他兩種算法，實驗取得了比較理想的效果。

[1]Shi Y，Eberhart R.Fuzzy adaptive particle swarm optimization[C]//Proceedings of Congress on Evolutionary Computation，2001，3（27）：101-106.

[2]Angeline P J.Using selection to improve particle swarm optimization[C]//Proceedings of the Congress on Evolutionary Computation，1998，3（4）：84-89.

[3]崔志華，曾建潮.一種動態(tài)調(diào)整的改進微粒群算法[J].系統(tǒng)工程學(xué)報，2005，20（6）：657-660.

[4]夏桂梅，曾建潮.雙群體隨機微粒群算法[J].計算機工程與應(yīng)用，2006，42（24）：46-48.

[5]王麗芳，曾建潮.基于微粒群算法與模擬退火算法的協(xié)同進化方法[J].自動化學(xué)報，2006，32（4）：630-635.

[6]Shi Y，Eberhart R C.Comparing inertia weights and constriction factors in particle swarm optimization[C]//Proceedings of the 2000 Congress on Evolutionary Computation.Conference Publications，2000（1）：84-88.

[7]Shi Y，Eberhart R.C.Recent advances in particle swarm[C]// Congress on Evolutionary Computation，2004（1）：90-97.

[8]Kennedy J，Eberhart R C.Particle Swarm Optimization[C]// IEEE International Conference on Neural Networks.Piscataway，NJ：IEEE Service Center，1995：1942-1948.

[9]李寧.粒子群優(yōu)化算法的理論分析與應(yīng)用研究[D].武漢：華中科技大學(xué)，2006.

[10]溫黎茗，彭力.用正弦函數(shù)描述非線性慣性權(quán)重的微粒群算法[J].計算機仿真，2012，29（5）：235-238.

QIN Yi,PENG Li

School of Internet of Things Engineering,Jiangnan University,Wuxi,Jiangsu 214122,China

This paper proposes nonlinear inertia weight particle swarm optimization with a filtering mechanism to improve the non-linear inertia weight particle swarm algorithm.Due to the original algorithm exsists two shortcomings of particles falling into the local optimal solution and lower search efficiency,introduces fitness scaling function to the nonlinear inertia dynamically for the particle swarm optimization,fitness of excellent and poor particle are removed,then copy some excellent individual of remaining population,meanwhile randomly generated new particles,and crossover operation to them,populations remain unchanged,the methed reduces the opportunity that particulates fall into the localmaximum and make the results converge to the global optimum.In order to verify the effectiveness of the algorithm.In this paper,low dimensions and high dimensional function are compared with each other.The result show s that this method achieves good effects.

filtering mechanism;fitness scaling;inertia weight;nonlinear particle swarm algorithm

A

TP39

10.3778/j.issn.1002-8331.1208-0478

QIN Yi,PENG Li.Non linear inertia weigh t particle swarm optimization with filtering mechanism.Computer Engineering and Applications,2014,50（16）：35-38.

秦毅（1987—），男，研究生，主要研究方向為智能決策系統(tǒng)與仿真；彭力（1967—），男，博士，博導(dǎo)，主要研究方向視覺傳感器網(wǎng)絡(luò)，人工智能，計算機仿真。E-mail：qinyidee@163.com

2012-09-04

2012-10-11

1002-8331（2014）16-0035-04

CNKI網(wǎng)絡(luò)優(yōu)先出版：2012-11-28,http://www.cnki.net/kcm s/detail/11.2127.TP.20121128.1453.006.htm l