大型汽輪機高壓進汽閥啟動過程換熱規律研究

陳永照， 黃 威， 王宇翔， 劉麗平， 忻建華

（1.上海交通大學 動力機械與工程教育部重點實驗室，上海200240；2.上海電氣電站設備有限公司，上海200240）

隨著汽輪機技術的不斷發展，運行參數不斷提高，運行方式逐漸多樣化，機組中各部件的換熱情況越來越復雜.一些高溫下運行的厚壁部件在機組啟動和變工況過程中容易受熱不均，產生較大的內部熱應力，如果熱應力控制不當，則直接影響機組安全性和役期內的壽命.目前，國內外針對高中壓汽缸、轉子等部件在啟動和穩定運行時的熱應力進行了較多的研究，并將其作為控制機組啟停和變負荷速率的依據之一［1－3］，而對于同屬高溫厚壁部件的高壓進汽閥，相關資料還比較匱乏.閥門啟停過程熱應力的計算與啟停各階段的傳熱系數有關，傳熱系數直接影響熱應力分析的正確與否.筆者以某超超臨界百萬機組的高壓進汽閥為例，通過計算和試驗比較的方法，分析機組啟動過程中主調閥門的換熱特性，得到了啟動和穩定運行的傳熱系數，為后續閥門熱應力的研究和控制提供依據.

1 啟動過程換熱分析

現代先進汽輪機主調閥的結構是將主蒸汽閥（以下簡稱主閥）和調節閥整合為一體直接安裝到高壓缸上，結構示意圖見圖1.這種形式的主閥和調節閥緊密相連，結構緊湊，壓損較小，但國內缺少對其啟停過程中換熱規律的研究資料.圖1中，蒸汽從主閥進口管道A進入主閥腔室B，在主閥閥門開啟狀態下經主閥和調節閥之間的連通管道進入調節閥腔室C，最后經調節閥出口管道D進入高壓缸.

圖1 某超超臨界機組高壓進汽閥結構示意圖Fig.1 Structural diagram of a USC HP valve

汽輪機組的啟動根據部件的初始金屬溫度不同分為冷態、溫態、熱態和極熱態4種方式，其中冷態啟動時閥門換熱情況最復雜，閥門的熱應力也最大，因此工程設計上可用冷態啟動過程來涵蓋另外3種啟動過程.筆者通過研究冷態啟動的傳熱過程以得到高壓主調閥的換熱規律.

圖2為機組實際冷態啟動過程曲線.圖中A時刻表示鍋爐點火開始啟動，此時主閥和調節閥均為關閉狀態.但鍋爐一旦產生蒸汽（蒸汽溫度110℃、壓力0.137MPa）即沿主蒸汽管道進入主閥腔室，開始預暖主蒸汽管道和主閥，此時蒸汽在管道內表面和主閥腔室壁面發生凝結換熱.隨著蒸汽參數不斷提高，主閥內壁金屬溫度（主壁溫）也不斷升高，但均低于主蒸汽壓力下對應的飽和溫度.此期間的高強度凝結換熱使主閥內壁金屬溫度快速上升，并保持與蒸汽壓力下的飽和溫度（汽飽溫）之間有一較小的溫差但又與飽和溫度變化趨勢一致，直到圖中B時刻二者溫度基本一致，凝結換熱結束，此時主閥內壁金屬溫度達282.7℃，蒸汽溫度為498.7℃、壓力為6.69MPa.此后主閥進入對流換熱階段.

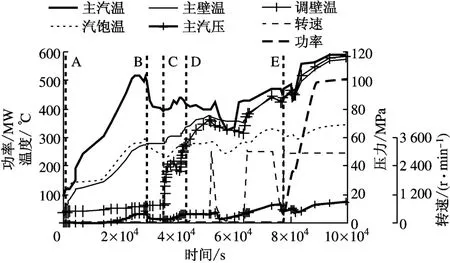
圖2 某超超臨界機組冷態啟動過程曲線Fig.2 Cold start－up curve of the USC unit

圖2中C時刻預暖管道和預暖主閥基本完成，主閥閥門打開，蒸汽進入調節閥腔室開始預暖調節閥.同樣，調節閥金屬壁面先與蒸汽發生凝結換熱，在D時刻進入單相對流換熱階段.在凝結換熱初期調節閥金屬溫度（調壁溫）幾乎呈階躍上升，最大溫升速率達33.2K／min，這主要是由于主閥開啟瞬間調節閥腔室內蒸汽壓力突升，蒸汽飽和溫度相應升高，對調節閥的金屬表面形成熱沖擊所致.

D時刻結束預暖調節閥，調節閥閥門微開，蒸汽進入高壓缸預暖轉子和內缸.此后在調節閥控制下進行了3次沖轉，E時刻成功并網帶負荷，然后進入升負荷和穩定運行階段.

整個啟動過程中，閥門溫度狀態的差異、蒸汽參數的波動以及流量的變化導致高壓進汽閥內換熱情況復雜，主閥和調節閥均先后經歷凝結換熱和單相對流換熱.凝結換熱階段換熱強度受蒸汽壓力影響明顯，單相對流主要受蒸汽溫度和流量影響.

2 傳熱系數計算

由第1節分析可知，閥門冷態啟動過程經歷了凝結和單相對流2個換熱階段.目前，國內外關于閥門內換熱規律的研究很少.傳熱系數多采用平板或圓管公式再考慮修正系數來計算.

凝結過程由于換熱劇烈，部分文獻將其作為第一類邊界條件，或取傳熱系數為一較大的定值［4］，這種處理方法忽略了蒸汽凝結產生液膜的熱阻以及凝結過程中液膜厚度的變化.考慮實際情況，可以分別選取努塞爾凝結換熱分析解中的豎壁、球面和柱面公式，來計算主閥進口管道、主閥和調節閥腔室、主閥和調節閥的連通管道和調節閥出口管道的凝結傳熱系數，計算公式如下

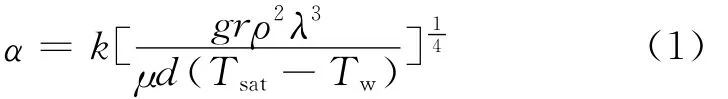
式中：系數k對應于球面、豎壁及柱面分別為0.826、1.13和0.729；ρ為飽和水的密度，kg／m3；λ為導熱系數，W／（m·K）；μ為動力黏性系數，Pa·s；r為潛熱，J／kg；Tsat和Tw分別為蒸汽壓力下的飽和溫度和金屬壁面溫度，℃；d為特征尺寸，m.

對于單相對流換熱，有學者研究得到2類計算傳熱系數的經驗公式.第一類公式為努塞爾數準則公式，如文獻［5］和文獻［6］所用分別以閥門入口管道直徑和管中流速作為特征尺寸和速度的準則公式

式中：閥腔部分系數k1＝0.046；閥腔進、出口管道系數k1＝0.021.

對管道的彎曲部位應加以修正

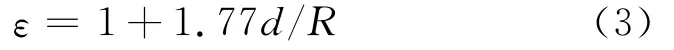
式中：d和R分別為管道直徑和彎曲部位的曲率半徑.

第二類公式是根據能量平衡方程利用實測數據計算傳熱系數，如熱平衡法［7］.

式中：cM、ρM分別為金屬比熱容和密度，J／（kg·K），kg／m3；h為金屬壁厚，m；Δt為 Δτ時間內蒸汽與壁面平均溫差，K，ΔtM為Δτ時間內金屬平均溫度變化值，K；kR和kz分別為考慮了壁面曲率和軸向導熱的修正系數，kR＝1＋h／2R；kδ為壁面真實溫度與距壁面δ處溫度測點間的溫差修正系數.

當溫度沿壁厚呈拋物線分布時，

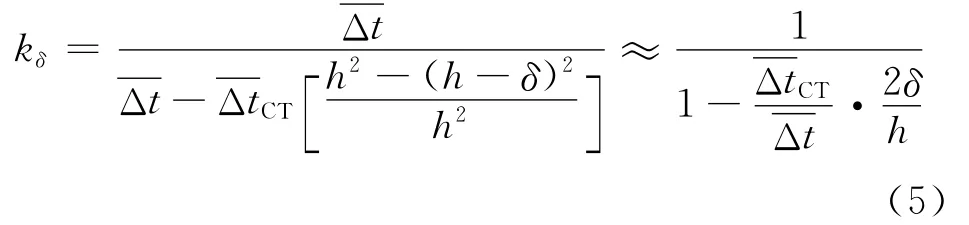
式中：ΔtCT為Δτ時間內沿壁厚平均溫差.

經實際應用發現，上述公式均存在一定的局限性.如式（2）由于缺少閥門啟動各時刻的準確流動參數而無法使用，式（4）對于結構復雜的閥門難以確定軸向導熱修正系數，另外由于各種類型閥門的結構差異較大，計算所得傳熱系數也存在較大誤差.

筆者根據實際情況，提出了確定傳熱系數的新方法——逐步逼近法.采用試驗和理論計算相結合的方法，并借助有限元分析軟件，利用迭代和修正傳熱系數計算溫度場，使各測點的溫度計算值與測量值吻合，最終得到傳熱系數.具體步驟如下：首先將整個啟動過程按閥門內的流動特點［8］分為若干計算時段，認為各時段內傳熱系數是常數或按線性變化.然后確定各時段傳熱系數迭代初始值.為了減少迭代次數和縮短計算時間，方便對現有傳熱系數計算方法的精度和適用性進行比較和評價，選用圖2所示的實際啟動曲線和相應的熱力參數，利用式（1）和式（4）計算所得凝結換熱階段和單相對流階段的傳熱系數作為迭代初始值，部分時段傳熱系數計算結果見表1.考慮到凝結傳熱系數與凝結水膜厚度直接相關，而水膜厚度主要受溫差ΔT＝Tsat－Tw的影響，所以表中凝結換熱時段大致按ΔT值劃分，表2類似.

表1 經驗公式計算所得傳熱系數Tab.1 Heat－transfer coefficient calculated by empirical formula W／（m2·K）

根據圖2的啟動曲線和表1的傳熱系數，利用有限元計算軟件對閥門進行了三維非穩態的溫度場計算.圖3為在整個啟動過程中主閥計算溫度和實測溫度的比較.從圖3可以看出，采用上述公式計算所得溫度在大部分時段內與實測值變化趨勢一致，但在升速、升負荷等過渡工況時偏差較大，最大偏差為56.8K，平均偏差為26.6K.

之后依據計算溫度和實測溫度的偏差對各階段的傳熱系數進行逐步修正.引入修正系數k2，則修正過程可表示為

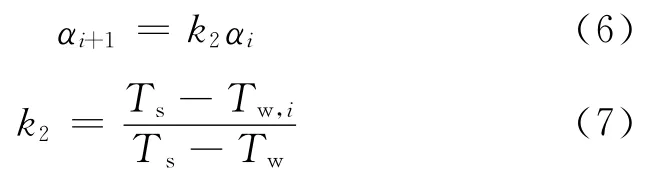
式中：αi、αi＋1分別為修正前、后的傳熱系數；Ts為加載溫度；Tw，i為αi計算的內壁面溫度.

用式（6）進行逐步逼近若干次傳熱系數修正和溫度場計算，若計算結果Tw，i與實測值Tw之差小于某一設定值（設定值主要由其對應力計算結果的影響程度確定，應確保在設定值范圍內應力計算結果不會有較大偏差），認為此時傳熱系數已充分逼近真實值，則停止逐步逼近修正過程.圖3給出了本例中經過3次傳熱系數修正后主閥計算溫度和實測溫度的差異，可以發現二者幾乎完全重合.進一步數據分析表明，二者最大溫度偏差為7.2K，平均溫度偏差為3.2K，此時應力計算偏差為4.8%，滿足工程設計的要求.傳熱系數部分計算結果見表2.

從上述對2種傳熱系數計算方法的介紹和計算結果的比較分析可以看出，經驗公式計算過程簡單，但結果準確度不夠；而逐步逼近法實用性強，雖然計算量稍大，但精度很高.因此，在實際應用中，對于較為粗略的分析，可以直接選用式（1）～式（4）計算傳熱系數，而對于要求較高的精確計算，可以在公式計算基礎上采用逐步逼近法進行修正，直至達到精度要求.

表2 逐步逼近法計算所得傳熱系數Tab.2 Heat－transfer coefficient calculated by step－by－step approach W／（m2·K）

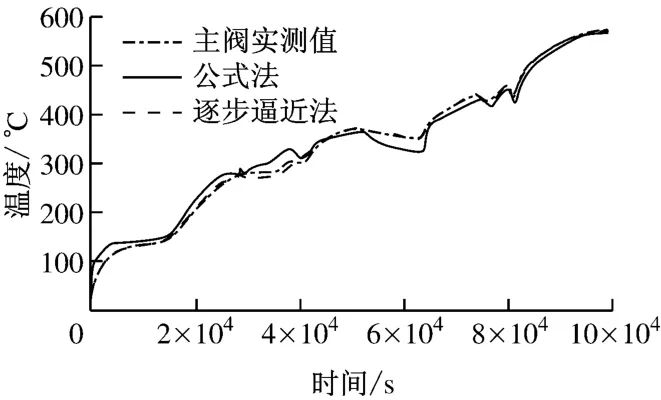
圖3 主閥溫度實測值與計算值的比較Fig.3 Comparison of main valve temperature between calculated results and actual measurements

3 傳熱系數適用性研究

逐步逼近法計算傳熱系數必須建立在一定的試驗數據基礎上，但在新閥門設計階段，往往缺少相應的試驗數據，因此要獲得精確的傳熱系數是困難的，只能根據經驗選取.針對這種情況需要進一步研究傳熱系數對于不同閥門的適用特點.

首先研究結構形式相同的閥門傳熱系數的適用性.圖4為另一組主調節閥的冷態啟動過程曲線，該啟動過程與圖2中基本一致，依次為暖主閥、暖調節閥、暖機、沖轉并網、升負荷和穩定運行，且閥門結構也基本相同.

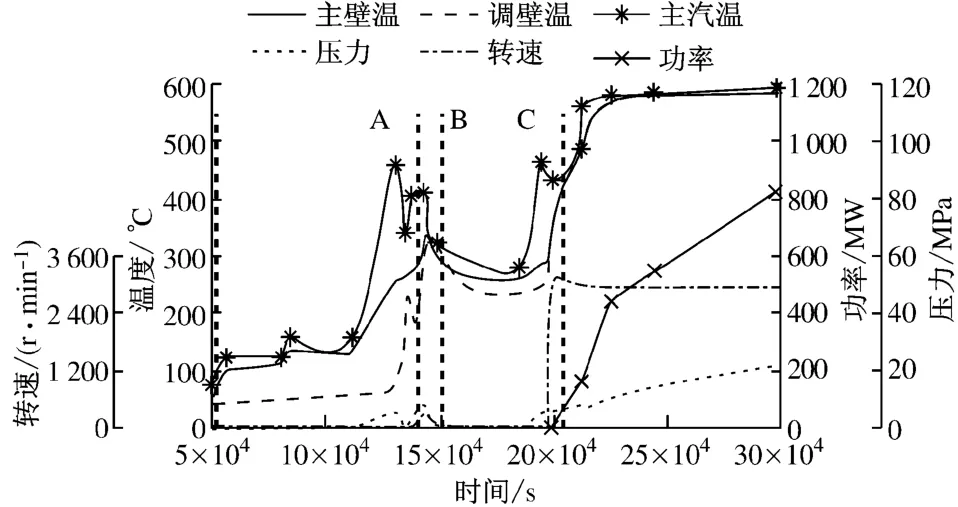
圖4 另一超超臨界機組冷態啟動過程曲線Fig.4 Cold start－up curve of another USC unit

將前面逐步逼近法所得各階段傳熱系數的選取規律（見表2）直接應用于這一啟動過程計算，并將計算溫度與實測值進行比較（見圖5），發現除了某些特殊時刻，如閥門突然開啟、關閉等，絕大部分時段的計算結果與實測值能很好地吻合，最大溫度偏差為16.9K，平均溫度偏差為5.7K，證明逐步逼近法所得傳熱系數對結構基本相同的閥門是適用的，這為不同蒸汽參數和容量的新閥門的熱強度設計、非穩態運行工況熱應力的計算和控制提供了依據.

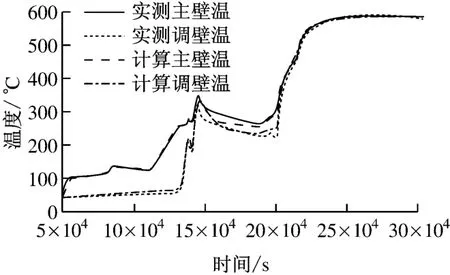
圖5 傳熱系數用于同類閥門時計算值與實測值的比較Fig.5 Comparison between actual measurements and calculated results with heat－transfer coefficient applied to same type of valves

然后研究不同型號閥門沿用傳熱系數的規律.圖6為某超臨界600MW機組高壓進汽閥的結構示意圖，其中A為主閥，B和C為調節閥，與圖1中閥門的差異較大.

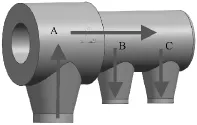
圖6 某超臨界機組高壓進汽閥結構示意圖Fig.6 Structural diagram of an SC HP valve

圖7為該機組的冷態啟動過程曲線，閥門所經歷的啟動階段與前述超超臨界機組基本相同，主要區別在于主閥閥門打開前調節閥已處于開啟狀態，因此開啟主閥之后暖調節閥與暖機同時進行.將表2中的傳熱系數選取規律直接應用于該機組閥門，計算啟動過程的溫度分布，并將計算結果與實際數據進行比較，結果見圖8.從圖8可以看出，在整個啟動過程中，計算所得主閥和調節閥內壁溫度與實測值變化趨勢一致，在C區計算值與實測值的偏差較小，但在主閥凝結換熱前期（A1區）和調節閥凝結換熱階段（A2和B區）計算結果明顯偏高（最大溫度偏差為33.6K），表明這些時段的傳熱系數比實測值偏大.這說明閥門結構和運行方式對傳熱系數影響較大.

圖7 超臨界機組冷態啟動過程曲線Fig.7 Cold start－up curve of the SC unit

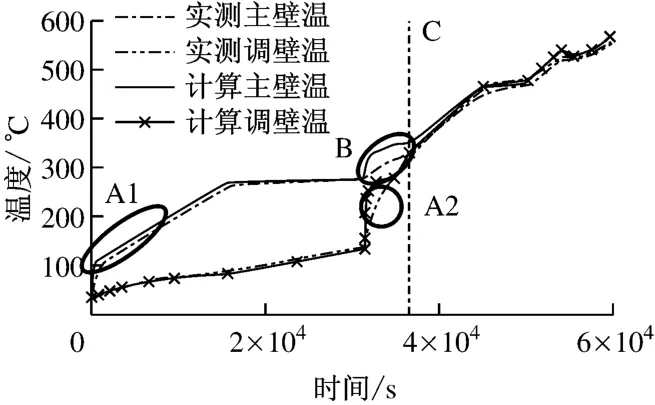
圖8 傳熱系數用于非同類閥門時計算值與實測值的比較Fig.8 Comparison between actual measurements and calculated results with heat－transfer coefficient applied to different types of valves

對比圖1中超超臨界機組的閥門，在暖調節閥階段主閥閥門開度較大，調節閥腔室內壓力和流量較大，換熱強度較高；而圖6超臨界機組的閥門暖調節閥和暖機同時進行，主閥閥門需要控制轉子轉速和暖機過程，因此開度很小（2%左右），調節閥腔室內的壓力低、流量小，換熱強度也相對較低，傳熱系數更小.若要得到這些時段的真實傳熱系數，需要采用逐步逼近法進一步計算.總體而言，不同結構的閥門間傳熱系數直接應用會因機組運行方式及閥門結構的不同產生一定的計算偏差，但可以滿足工程中粗略計算的要求，具有一定的借鑒意義.因此，在設計不同于圖1所示的閥門結構時，可以用表2所示的閥門在不同階段的傳熱系數進行熱強度設計和啟停過程的熱應力控制，在閥門投入運行后，根據閥門的實測數據采用逐步逼近法求得更為精確的傳熱系數，對閥門的熱應力控制過程進行修正，以保證閥門在役期內的安全.

總結傳熱系數在不同閥門間的適用特點發現，對于結構基本相同的閥門，若機組運行方式相同，則傳熱系數是直接適用的，計算產生的偏差較小；而當結構不同、機組運行方式存在一定差異時，為滿足較高精度的計算要求，閥門傳熱系數應根據實際運行方式差異進行適當修正.

4 結 論

（1）機組冷態啟動時高壓進汽閥內換熱情況復雜，閥門各部位與蒸汽均先后進行凝結換熱和單相對流換熱，為避免熱沖擊，凝結換熱階段應限制蒸汽的壓力，單相對流換熱階段則要控制蒸汽溫度和流量.

（2）總結當前文獻提供的閥門傳熱系數計算公式，并根據實際情況提出逐步逼近法.在實際計算中比較二者的計算效果，發現公式法因實際情況的復雜性存在一定的偏差，而逐步逼近法計算所得傳熱系數具有較高的可信度.

（3）對閥門傳熱系數適用性的研究發現，相同結構和運行方式的閥門間傳熱系數可以通用，不同結構和運行方式的閥門間傳熱系數直接應用會在某些時段產生一定的偏差，但整體效果良好.這為傳熱系數的簡化計算和相互借用提供了重要依據，所得傳熱系數選取規律也可推廣應用.

（4）對于獲取傳熱系數的方法，建議在有實際運行數據時，根據式（1）～式（4）初步計算，若要準確計算，可在逐步逼近法的基礎上進行適當修正；在沒有實測數據的情況下，比如新閥門的設計，可以直接選用本文提供的傳熱系數，其計算結果滿足近似計算要求.

［1］支小牧，寇可新，曹向欣.汽輪機轉子熱應力在線監測、壽命管理及優化啟動的研究［J］.動力工程，2000，20（1）：543－548.ZHI Xiaomu，KOU Kexin，CAO Xiangxin.Steam turbine rotor thermal stress on－line supervision，life management and optimal start－up study［J］.Power Engineering，2000，20（1）：543－548.

［2］鄭李鵬，陳堅紅，盛德仁，等.燃氣－蒸汽聯合循環汽輪機快速啟動的研究［J］.動力工程學報，2011，31（8）：579－584.ZHENG Lipeng，CHEN Jianhong，SHENG Deren，et al.Study on quick start up of steam turbine in a gassteam combined cycle［J］.Journal of Chinese Society of Power Engineering，2011，31（8）：579－584.

［3］方寧，紀冬梅，姚秀平，等.基于徑向基函數神經網絡的汽輪機轉子等效應力計算模型［J］.動力工程學報，2011，31（4）：268－272.FANG Ning，JI Dongmei，YAO Xiuping，et al.Computation model for equivalent stresses in steam turbine rotors based on RBF neural network［J］.Journal of Chinese Society of Power Engineering，2011，31（4）：268－272.

［4］王宏光，戴韌，劉巖，等.超臨界汽輪機閥殼的溫度場和應力場計算分析［J］.上海理工大學學報，2007，29（1）：75－78.WANG Hongguang，DAI Ren，LIU Yan，et al.Numerical analysis of temperature and stress field in valve housing of super critical steam turbine［J］.Journal of University of Shanghai for Science and Technology，2007，29（1）：75－78.

［5］彭震中，丁祝順，王璋奇，等.汽機調節閥閥體三維瞬態溫度場及應力場分析［J］.熱能動力工程，2002，17（1）：81－83.PENG Zhenzhong，DING Zhushun，WANG Zhangqi，et al.Numerical analysis of temperature and stress field in control valve housing of a steam turbine［J］.Journal of Engineering for Thermal Energy and Power，2002，17（1）：81－83.

［6］李德生，荊建平，孟光.汽機閥殼瞬態溫度場及應力場仿真分析［J］.汽輪機技術，2008，50（1）：6－8.LI Desheng，JING Jianping，MENG Guang.Numerical simulation of temperature field and stress field of the valve box of a steam turbine［J］.Turbine Technology，2008，50（1）：6－8.

［7］普羅特金，列依澤羅維奇.單元發電機組汽輪機啟動工況［M］.夏同棠，譯.北京：水利電力出版社，1985：48－52.

［8］朱奇，谷傳綱，戴韌.超超臨界百萬千瓦汽輪機主調節閥流場非穩態數值研究［J］.動力工程學報，2010，30（10）：743－748.ZHU Qi，GU Chuangang，DAI Ren.Numerical simulation on unsteady flow field in the main stop and control valve system of a 1 000MW ultra－supercritical steam turbine［J］.Journal of Chinese Society of Power Engineering，2010，30（10）：743－748.