基于多變量內模解耦的CFB鍋爐燃燒控制研究

鐘亮民， 劉吉臻， 張 恒， 王瑞琪

（華北電力大學 控制與計算機工程學院，新能源電力系統國家重點實驗室，北京102206）

循環流化床（CFB）鍋爐作為傳統火力發電技術的重要和有益補充，近年來越來越受到重視.高參數、大容量的超臨界CFB鍋爐機組正處在試點實踐過程中.但無論參數和容量如何變化，CFB鍋爐的自動控制問題始終是重點和難點.CFB鍋爐是一個集流動、傳熱和燃燒等諸多過程于一體的復雜系統，其控制對象具有多參數、非線性、大滯后、大慣性和多變量緊密耦合的特點，部分控制對象還有右半平面（RHP）零點，具有反向響應特點.這些特點給CFB鍋爐燃燒系統的自動控制帶來很大困難.CFB鍋爐燃燒控制的目的是維持穩定的主蒸汽壓力并保持一定的床溫.通常選取一次風量－床溫和給煤量－主蒸汽壓力作為主控制通道，但這兩者之間存在強耦合，且主通道和干擾通道的對象特性差別很大，解耦是必要且困難的，即使是超臨界CFB鍋爐，解耦也依然是首要任務［1］.

內模控制（IMC）因其魯棒性強、設計和整定簡單明了等特點而受到關注.王東風等［2］先對對象進行補償解耦，使之成為對角陣或者對角占優矩陣，然后對廣義對象進行內模控制.JIN Qibing等［3］提出的基于V規范型對象預補償解耦方式是對文獻［2］中方法的發展.楊錫運等［4］提出主通道解耦，將其余通道看做是干擾通道.比較常用的是 Wang等［5］提出的解析解耦算法，該控制器兼具解耦和控制的作用.周平等［6］在文獻［5］方法的基礎上提出優化實際工業過程運行的解耦措施.Chen等［7］將內模控制用于Smith遲延補償控制器的設計，并應用于一階遲延多變量非方系統中.靳其兵等［8］從解耦和零穩態誤差兩方面入手，考慮系統穩態值，避免了模型降階的問題，簡化了遲延問題的處理.

筆者針對CFB鍋爐燃燒控制系統主蒸汽壓力和床溫的強耦合性、大慣性和大遲延的特點，采用多變量內模控制，通過解析的代數方法，使由于模型求逆而產生的預測項和不穩定極點得到補償.在設計過程中通過對遲延項的適當逼近措施和次最優降階方法的使用，使得控制器便于工業實現.設計濾波器將控制器中的閉環緩慢極點或主導極點抵消，使系統響應加快并能夠有效改善響應性能.濾波器時間常數的整定采用對控制量與輸出值的瞬時性能指標（調節時間和超調量）線性求和來衡量.在該優化條件下，進行系統的輸入擾動、輸出擾動響應，并對模型匹配和失配情況下系統的魯棒性進行驗證.

1 對象提出

馬素霞等［9］通過對75t／h CFB鍋爐進行機理分析并建立數學模型，研究其燃燒系統的動態特性，給出在70%～110%負荷下CFB鍋爐多輸入多輸出（MIMO）燃燒系統的傳遞函數矩陣.筆者選取主蒸汽壓力和床溫這對強耦合變量所構成的2×2矩陣作為研究對象.給煤量同時影響控制系統的很多重要參數，對主蒸汽壓力、床溫和煙氣含氧量的影響尤其明顯，給煤量突然增加會使主蒸汽壓力和床溫升高而煙氣含氧量降低.床溫的控制是通過調節一次風量來實現的，一次風量對燃燒起著主導作用，其作用是維系爐內和分離器內的物料循環流化，提供燃料燃燒的大部分氧氣.一次風量的相對穩定對CFB鍋爐的安全穩定運行至關重要.

一般認為，給煤量的變化首先將引起床溫的變化，由于CFB鍋爐內部蓄熱量很大，所以床溫的變化有較大遲延，而爐內工質溫差的存在則造成爐內傳熱狀況發生改變，于是主蒸汽壓力也隨之改變.本文除特殊說明外，床溫均指密相區床料溫度.控制床溫的目的是保持爐體內密相區床溫在850～950°C最佳流化溫度區間內.當通過改變一次風量調節床溫時，床溫的反應迅速，幾乎沒有遲延.但一次風量調整幅度與其對爐內物料流化的影響正相關，因此將引起主蒸汽壓力的波動.另外，最小流化風量是一次風量的下限.考慮解耦的燃燒系統控制結構框圖見圖1.

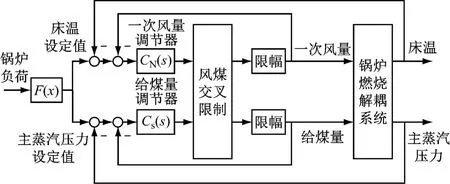
圖1 考慮解耦的燃燒系統控制結構圖Fig.1 Structural diagram of the combustion control system considering decoupling

根據文獻［9］的階躍擬合關系，該燃燒系統動態特性可描述為

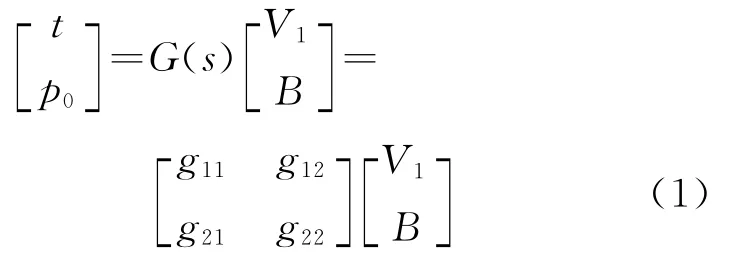
式中：t為床溫，℃；p0為主蒸汽壓力，MPa；V1為一次風量，m3／h；B 為給煤量，kg／h；d1為系統輸入擾動量；d2為系統輸出擾動量；G（s）為控制通道傳遞函數矩陣.

G（s）的組成為

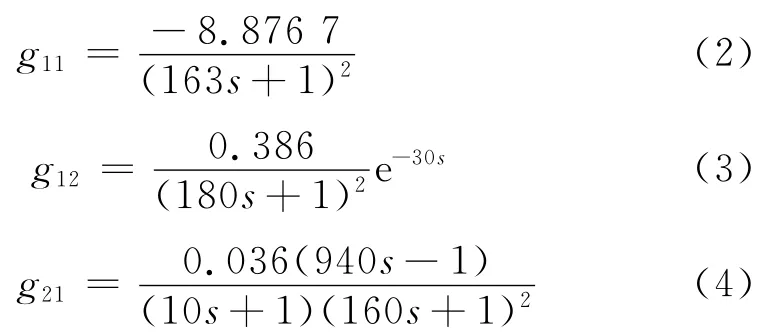
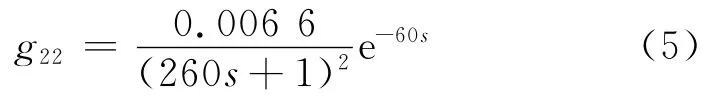
由式（2）～式（5）可見，有些對象為階數大于2的高階對象，同時還含有RHP零點.對該兩輸入兩輸出（TITO）系統作階躍響應，可反映出每一條控制通道對象的慣性大、自平衡時間長的特點.由于RHP零點的存在，一次風量變化對主蒸汽壓力的影響有逆向響應特性.2個通道均存在耦合，相對增益矩陣為

根據控制理論，當通道的相對增益λij＜0.7或λij＞1.3時，表明系統存在嚴重耦合，需要進行解耦設計.在工業中，控制對象以上特點的綜合是傳統PID控制器難以勝任的.

2 多變量內模控制器的設計

與傳統反饋控制相比，內模控制的主要優點是容易獲取良好的動態響應，同時能兼顧穩定性和魯棒性.內模控制系統結構框圖見圖2.其中，G（s）是系統實際過程對象，一般不能確切得知；G＾（s）是對象的過程模型；d1（s）是輸入擾動；d2（s）是輸出擾動；C（s）是內模解耦控制器；E（s）為模型失配時的系統偏差；u是控制器輸出量；r和y分別是系統設定值和輸出值.不同于單輸入單輸出（SISO）系統，在MIMO系統中，G（s）、G＾（s）和C（s）均為矩陣，各輸入輸出均為向量.

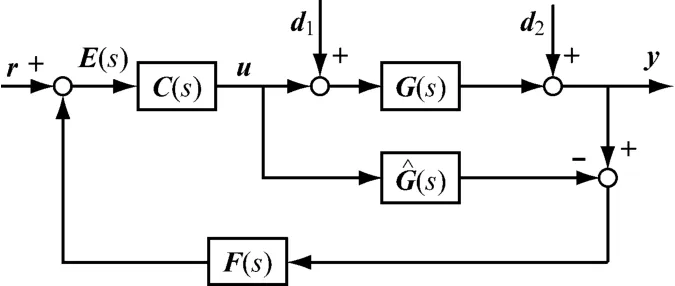
圖2 內模控制結構框圖Fig.2 Structural diagram of the IMC system

2.1 最優控制器設計

按照常規內模控制器設計二步法，由圖2可得系統閉環傳遞函數H為

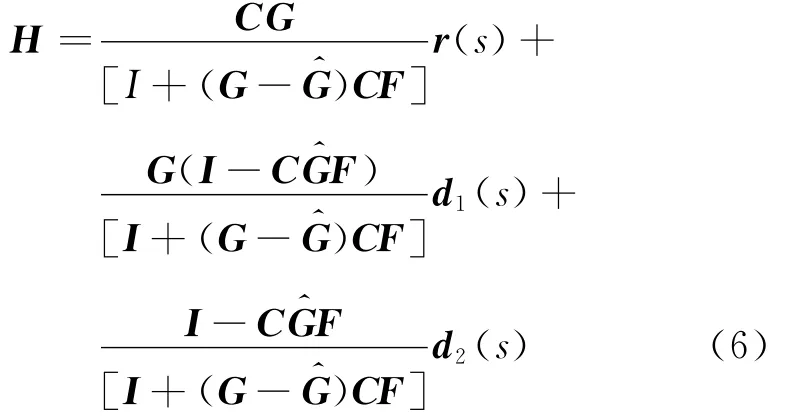
首先設定系統為標稱情況，即G（s）＝G＾（s）.不考慮擾動有H＝CG.對于如本文中各控制通道均穩定的對象，系統穩定的充要條件是C穩定.易知，最優解耦控制器為

由于絕大多數工業對象都含有遲延，有些還含有RHP零點，因此由式（7）得到的控制器具有預測項，在實際工業過程中無法實現.而RHP極點則使系統不穩定.在推導中，通常將過程對象分解為全通部分（all－pass）和最小相位部分，如

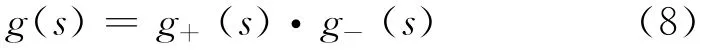
式中：g＋（s）包含所有的時滯項和RHP零點；g－（s）是對象穩定最小相位部分.

在此基礎上，為使控制器在階次上能夠實現，同時保證模型失配時的魯棒性，在控制通道上增加一個低通濾波器f（s），則內模控制器為

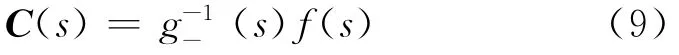
許多文獻指出，為進一步增加對模型誤差的魯棒性，可以在反饋回路上再增加反饋濾波器F（s）.一般以F（s）＝I為單自由度控制，否則為二自由度控制.對于遲延對象的二自由度控制，F（s）的時間常數通常取通道遲延時間的一半［10］.

對含有遲延和RHP零點的多變量對象模型傳遞函數矩陣進行類似分解過程稱為內外分解.一般的數值內外分解方法［11］對含遲延項矩陣的分解能力還有待研究.文獻［5］中提出的方法計算量較大.Zhang等改進了最優解耦控制器的代數設計過程，通過添加補償項來消除設計中包含的不可實現和不穩定因素［12－13］.考慮如下穩定的、同時含有不同時滯項和 RHP零點的2×2對象模型矩陣G＾（s）.G＾（s）的形式如下

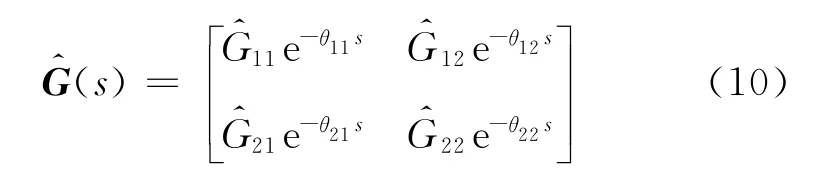
對象模型分解為非最小和最小相位的結果為

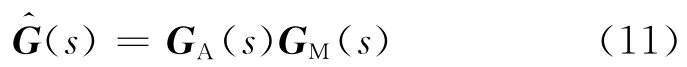
式中：GA為非最小相位部分；GM為最小相位部分；的逆矩陣存在，為

顯然，最優解耦控制器為

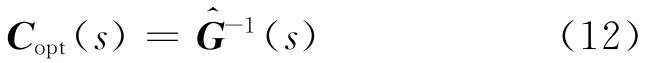
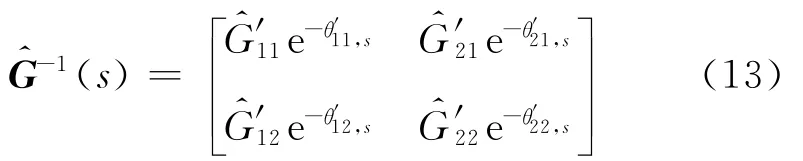
首先處理遲延項.將式（12）等式右邊乘以GD（s），GD（s）的形式為

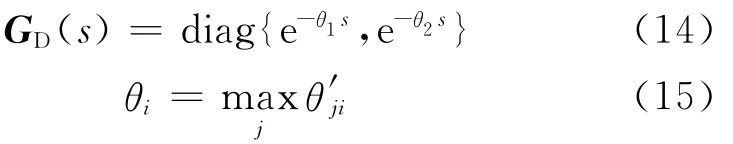
即θi是中第i列的最大遲延項.由此可知所選取的GD（s）可以抵消模型逆中的預測項，并且是唯一的.令相乘結果為則新的控制器為

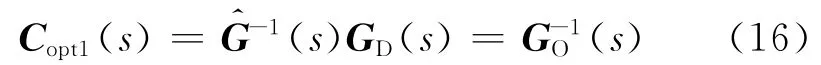
需要指出，相比SISO系統，由于RHP零點的存在必然導致不穩定極點的出現，在MIMO系統中，對象元素有公共零點時才一定成立.對于任意一個被控對象，當進行到

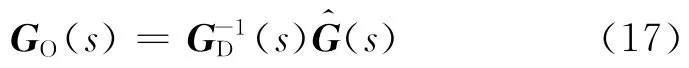
由于GD（s）為僅含時滯項的對角矩陣，不對G＾（s）的零極點分布產生影響.因此，

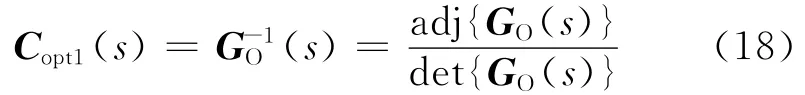
其中det｛GO（s）｝可能使某些元素不穩定.對于這些不穩定極點，將式（16）等式右邊乘以GN（s），使所有RHP極點被抵消，GN（s）的形式如下

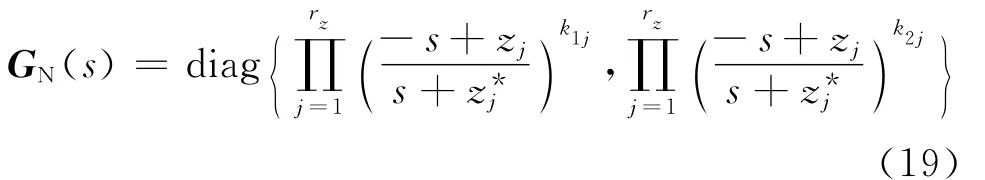
其中zj（j＝1，2，…，rz）是（s）中第j列元素RHP極點因式的最小公因式的各個極點.此時，

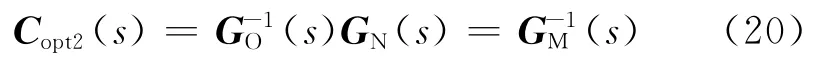
于是便得到了內模控制器Copt2（s）.易知，

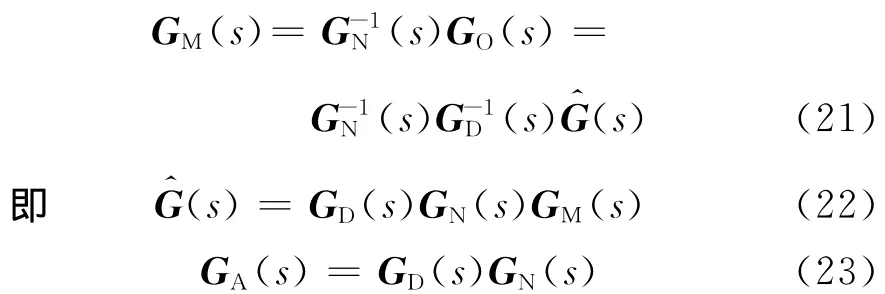
需要指出的是，解耦的完成是以可能引入更多的遲延項或者引入更多的RHP零點到控制器中為代價的.

2.2 濾波器設計

為柔化控制作用和平滑輸出響應的作用而引入的濾波器f（s）的形式一般為

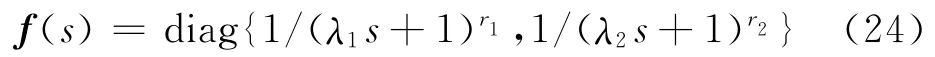
式中：r1、r2的取值使控制器可實現即可；λ1、λ2為濾波器的時間常數，是控制器中唯一可調的參數，其取值是系統響應快速性與魯棒性的折中.

Horn等［14］通過在濾波器分子上引入可調參數抵消被控過程中（對象）的緩慢極點，以加強抗負荷擾動的能力.改進濾波器的形式如下

類型1

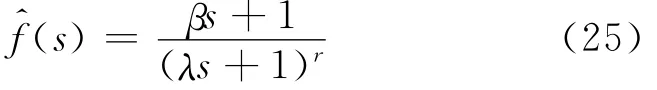
類型2

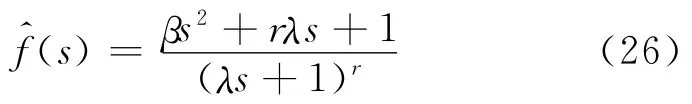
文獻［14］要在實現零極點抵消的同時，λ、β的值唯一確定，因此無法對輸出響應性能進行調節.受此啟發，筆者引入如下類似的濾波器矩陣

類型1

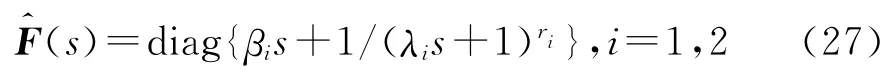
類型2

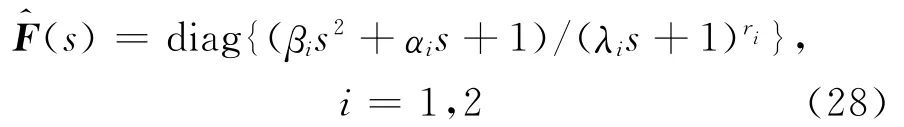
將其中的分子部分設計為可抵消緩慢極點或緩慢共軛極點的因式形式，λ1、λ2為可調待定參數.由上述可知，反饋回路濾波器為

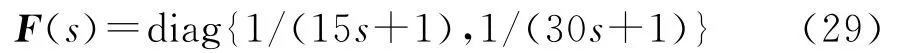
2.3 參數整定設計

理論上，所有優化算法再輔以合適的性能指標判定函數都可以應用于控制器參數的優化過程.前人對遺傳（GA）算法、粒子群優化（PSO）算法和NLJ算法等進行了不少研究.性能指標普遍采用綜合ISE或ITAE指標［15］.筆者選取輸出量和控制量的調節時間和超調量作為性能指標，同時兼顧對系統輸出和控制器輸出量的影響，并以潘立登［16］發展的NLJ算法作為尋優算法求取λ1和λ2在指定性能指標要求下的優化值.NLJ算法的具體過程在文獻［16］中有詳細論述，此處不再贅述.性能指標如下：

當r1＝1，r2＝0時

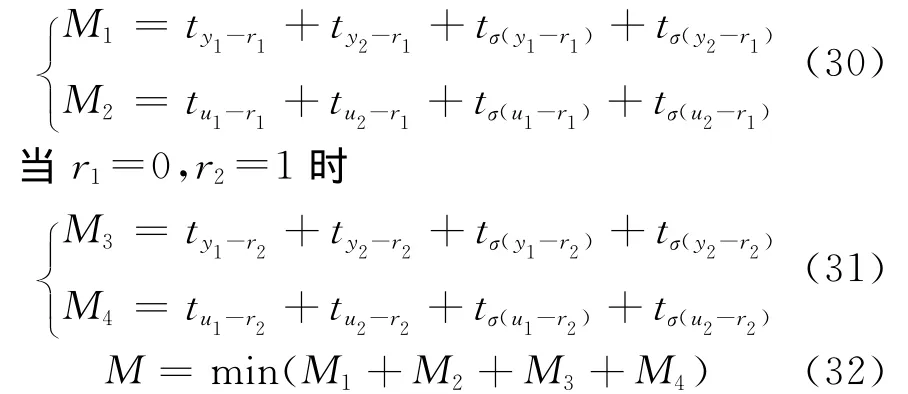
式中：ty1－r1和ty2－r1分別表示r1階躍、r2不變時y1和y2的調節時間；ty1－r2和ty2－r2分別表示r2階躍、r1不變時y1和y2的調節時間；tσ（u1－r1）和tσ（u2－r1）分別表示r1階躍、r2不變時y1和y2的最大超調對應的時間；tσ（u1－r2）和tσ（u2－r2）分別表示r2階躍、r1不變時y1和y2的最大超調對應的時間；其余符號的意義由此推知.

這樣的設計可使所有被求量具有同樣的量綱，且數量級相當，避免了“數量級淹沒”的現象，優化可信度高.需要指出，在只能改變濾波器常數的情況下，調節時間和超調量是矛盾量.筆者設定系統輸出量終值的誤差容限為±2%，以此尋找調節時間和調節穩定性的最佳平衡.控制器輸出量的誤差容限為終值的±10%，在實際中控制器輸出限值一般應超過穩態值1／3，以確保控制器和表計安全.

3 CFB鍋爐燃燒系統內模解耦控制

3.1 求取（s）

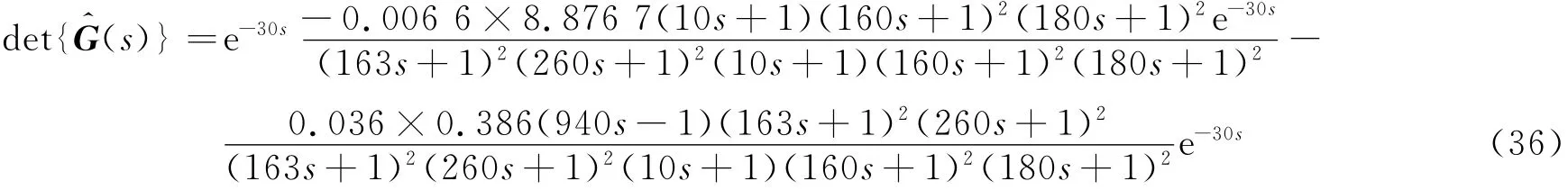
式（35）為高階有理式，為方便后續控制器的設計，應對其進行有效的模型降階處理.與整定濾波器常數類似，不少基于某些逼近條件的優化算法也被廣泛應用于模型降階中.文獻［17］中提出采用性能指標J的次最優降階方法.

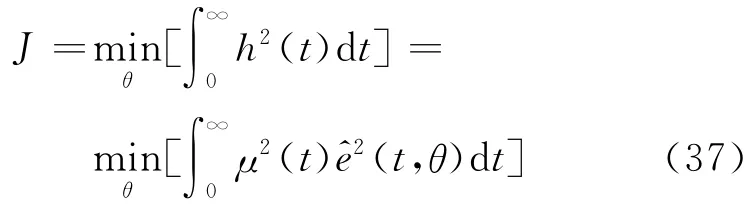
式中：h（t）為加權誤差信號，h（t）＝μ（t）e＾（t）；e＾（t）為原始模型與降階模型在相同輸入信號下的誤差，其中含有的遲延項采用pade逼近近似；μ（t）＝tp為權重函數.易知，當p＝0時，h（t）為ISE指標；當p＝1時，h（t）為ISTE指標.

該降階方法的特點是能夠相對獨立地選擇降階后模型分子、分母的階次以及降階后是否有遲延項，使用靈活，拓寬了其適用范圍.方法中pade逼近的階次亦可自由選擇，而pade逼近可以任意精度逼近遲延項，借助計算機工具，降階模型的精度得到保證.注意到式（35）的分母內部含有遲延項e－30s需要近似處理.尹先斌等［18］指出對于大遲延對象，一階pade逼近可以獲得滿意效果，而全極點逼近則適用于所有時滯過程，可以獲得較好的階躍響應.2種逼近方法的形式如下：

一階pade逼近

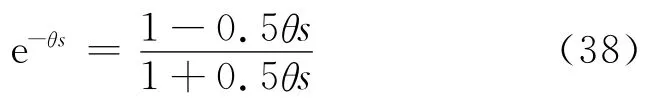
全極點逼近

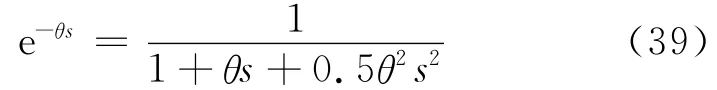
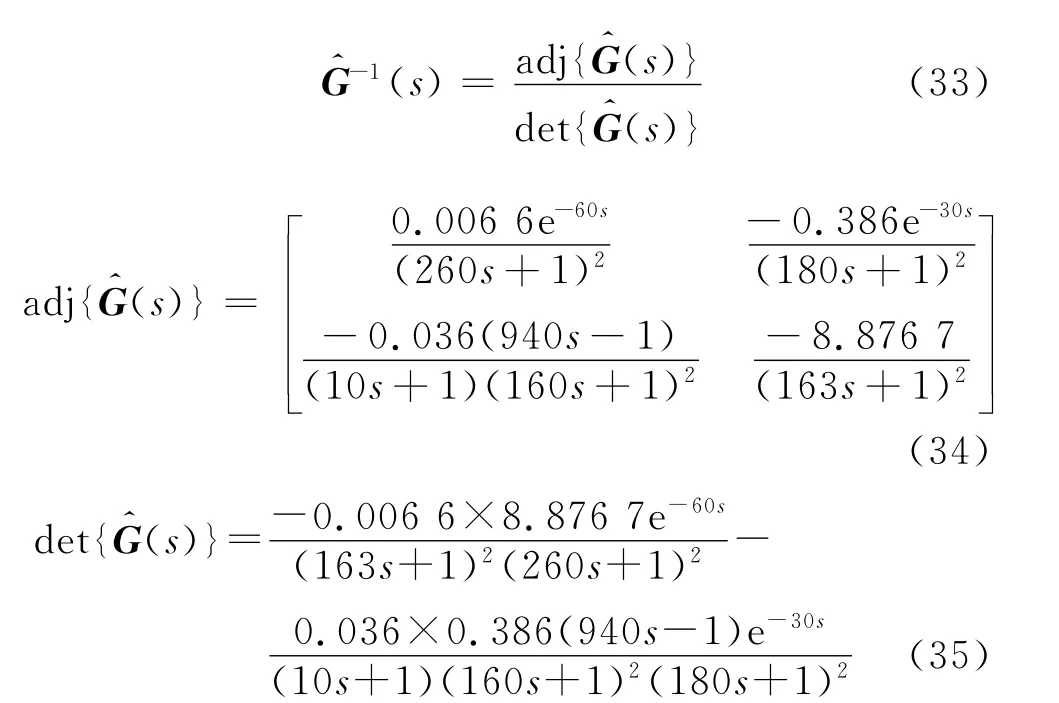
式（34）的理論遲延為30s.等式右邊提取e－30s后通分的結果為

將原始對象與一階pade逼近、全極點逼近效果進行比較發現，逼近效果差別細微.一階pade逼近略好于全極點逼近，故本文選擇前者.應指出，遲延項為公因式的一階pade逼近將引入新的極點，而全極點逼近則不會引入新的極點.但對于分式內部的遲延項，一階pade逼近與分子極點個數無直接關系.

應用次最優降階方法對上述對象進行降階，以不同階次pade逼近對遲延項進行近似，比較后發現三階pade逼近的效果較好.將對象降階到分子、分母均為2階且帶遲延的低階有理式

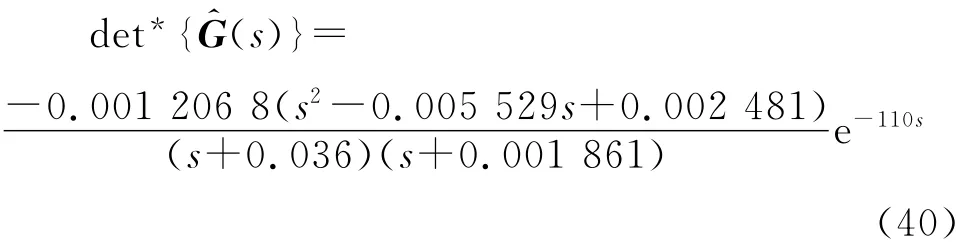
對比降階前后對象的階躍響應和Nyquist曲線，證實該方法的降階效果較好.

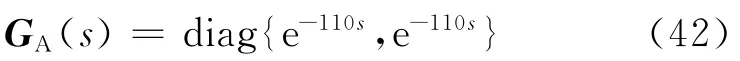
同時可知，矩陣各元素無零極點對消，故由等式

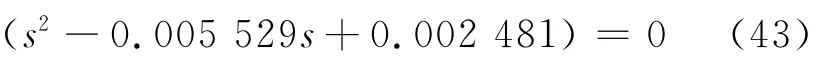
得到的根即為各元素唯一的公共不穩定極點.由此可知

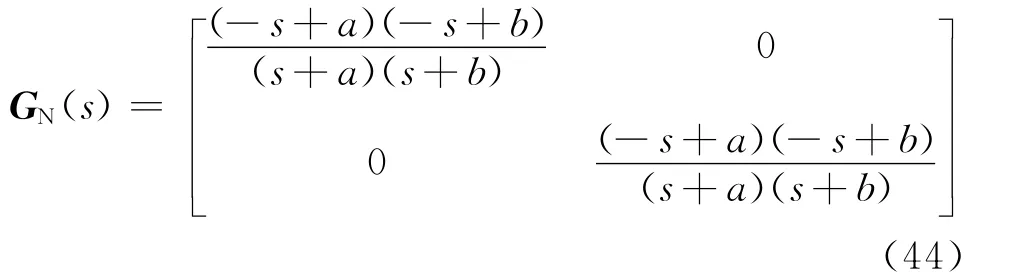
式中：a、b是式（38）的2個根，為共軛復根.

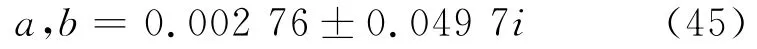
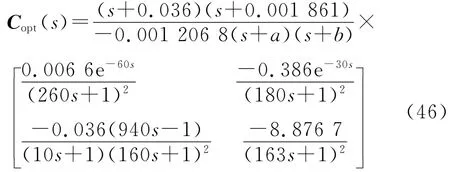
3.3 濾波器設計

考慮采用改進的濾波器設計方法來改善系統調節性能.注意到Copt（s）各元素中的緩慢極點（最靠近虛軸的點）均為因式（s＋a）（s＋b）的共軛復根，因此選取式（28）類型2作為濾波器的形式.為抵消該緩慢極點，可求得濾波器分子中β1＝β2＝403.063，α1＝α2＝2.229，分母階次取2可滿足要求，于是濾波器的形式變為

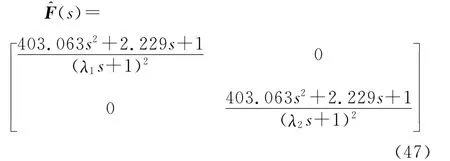
因此，得到控制器C（s）的各個元素為

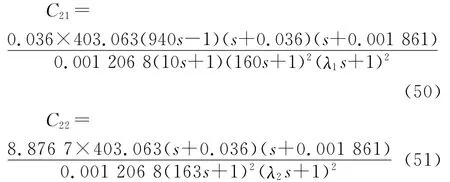
3.4 整定濾波器參數

筆者在大量的仿真實踐中發現，對于本文對象，若采用ISE指標，指標持續單調遞減，若采用ITAE指標，極小值點對應的λ1、λ2值在0.05附近.過小的時間常數將會降低系統的魯棒性，同時超調量也偏大.

筆者采用基于NLJ算法尋優的綜合了超調量和調節時間的性能指標，如2.3節所述.對于NLJ算法尋優的初始值，一般認為只要數量級相當即可［15，3］，選取＝80＝80.將初始參數代入算法中迭代尋優50次，得到優化的時間常數值λ501＝86.618，λ502＝204.627.NLJ算法具有良好的收斂性，通常迭代20～30次即可找到最優值.

3.5 仿真分析

符號說明：r1為一次風量；r2為給煤量；u1為一次風量－床溫通道控制器輸出；u2為給煤量－主蒸汽壓力通道控制器輸出；y1為床溫對象輸出；y2為主蒸汽壓力對象輸出.

在標稱情況下，且λ1＝86.618，λ2＝204.627，將改進濾波器的系統輸出響應與式（24）形式的傳統濾波器以及改進濾波器但固定時間常數（λ1＝λ2＝1.114）的系統輸出響應進行比較，如圖3所示.

以各變量響應保持在終值±2%作為調節進入穩態的指標，則可得表1和表2所示的性能指標.

同樣條件下，比較控制量輸出的響應（見圖4）.比較圖4所示的輸出階躍響應可知，無論采用何種形式的濾波器，對象耦合效應均較好地解除，2個變量不相互影響.由表1和表2可知，對于控制通道的跟蹤響應，將時間常數固定不變時，波形固定，調節時間和超調量等參數都較大，而且振蕩也較其他方法劇烈.傳統濾波器擁有最短的調節時間，但其超調量和振蕩程度均大于不固定時間常數的改進濾波器.改進濾波器在優化參數后，擁有最平穩的控制曲線，但犧牲了調節時間.應指出，改進濾波器未有效縮短調節時間，原因在于對象的緩慢極點并非其閉環主導極點.各極點與虛軸的距離基本處在相同數量級，抵消緩慢極點未能有效改善響應速度.共軛負根極點比距虛軸相同距離的實數極點有更快的響應，抵消緩慢極點的同時引入了更多的極點個數，使得改進濾波器方法的調節時間變長.

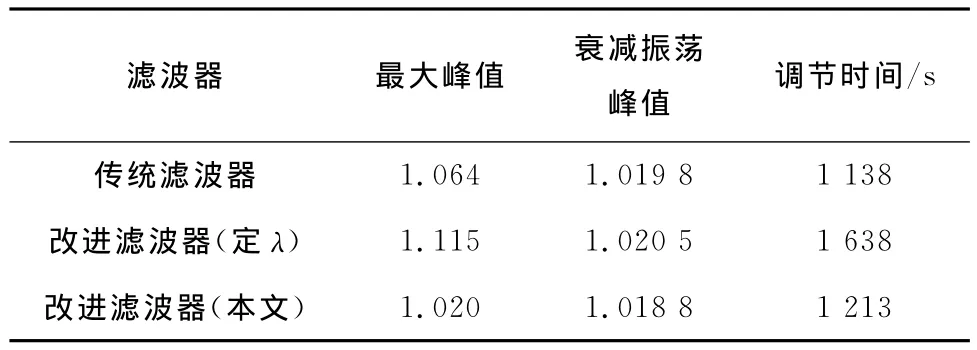
表1 r1＝1、r2＝0時y1的輸出指標Tab.1 Output index of y1in the case of r1＝1and r2＝0

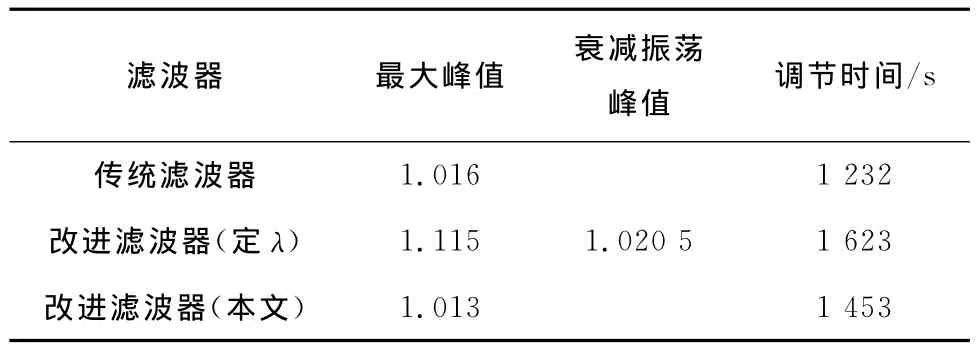
表2 r1＝0、r2＝1時y2的輸出指標Tab.2 Output index of y2in the case of r1＝0and r2＝1

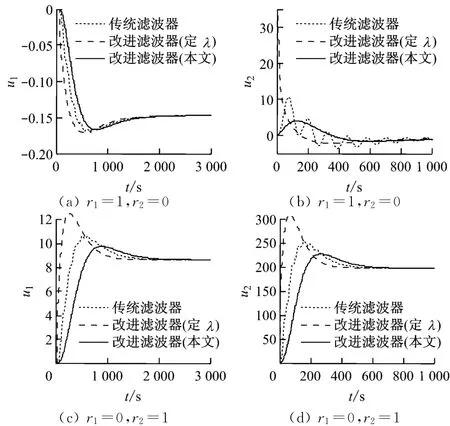
圖4 控制量輸出曲線的比較Fig.4 Comparison of control output curves among various filters

由控制量輸出曲線可知，盡管不固定時間常數的改進濾波器依然表現出較長的調節時間，但平滑性很好，且控制器的動作幅度比另2種方法明顯小很多.其中，固定時間常數的改進濾波器的動作量有時有突變，而傳統濾波器則在調節過程中表現出明顯的來回振蕩，對控制器不利.綜合上述，就控制的平穩性而言，不固定時間常數的改進濾波器有明顯優勢，且分析表明對于含主導極點的控制過程，抵消主導極點可以明顯延長調節時間.

為驗證控制系統的抗干擾能力，分別在過程對象前加入階躍擾動，觀察輸出響應曲線.在2次仿真中，分別從床溫和主蒸汽壓力對象兩者中的一個輸入端加入設定值30%的擾動量（3 500s時），并觀察另一輸入端是否受影響，結果示于圖5.

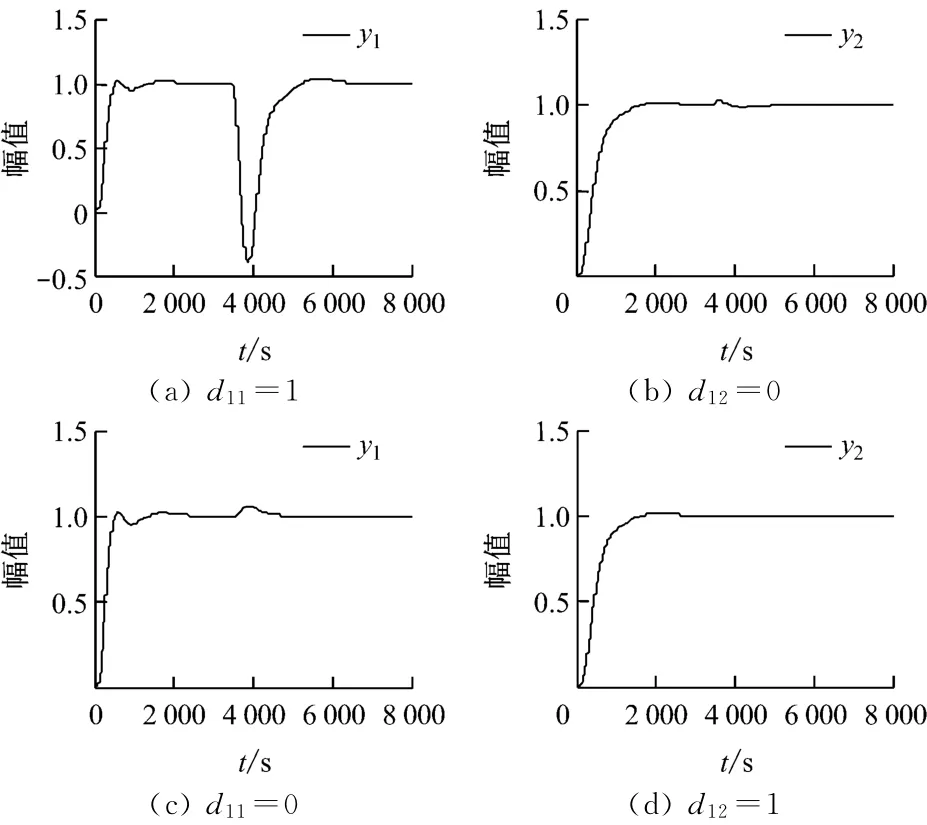
圖5 輸入擾動響應曲線Fig.5 System response under input disturbance

由圖5可知，對于床溫對象，在其輸入端加入擾動時，響應出現明顯的負調現象，這是由于一次風量階躍升高確定的床溫為負相關對象，干擾轉化為風量信號疊加在一次風量上傳遞給對象，床溫下降.負調幅度與該通道傳遞函數的增益成正比，同時也與擾動強弱有關.主蒸汽壓力輸入端的擾動對主蒸汽壓力特性幾乎沒有影響.主蒸汽壓力和床溫在另一對象發生擾動時均有小幅波動，但均能迅速得到抑制.階躍響應反映出系統能夠有效地抑制輸入擾動，但抑制效果仍需改善以達到更佳效果.

同理，在對象輸出端加入階躍擾動，觀察輸出的響應曲線.在2次仿真中，僅在不同對象的輸出端加入設定值30%的擾動量（3 500s時），得到系統對輸出擾動的響應曲線（見圖6）.

由圖6可見，解耦系統對輸出階躍擾動具有良好的抑制作用，主蒸汽壓力和床溫幾乎不受另一被控對象輸出端擾動的影響.顯然，濾波器時間常數的選擇影響平復時間的長短，較小的時間常數有加快響應速度的作用.

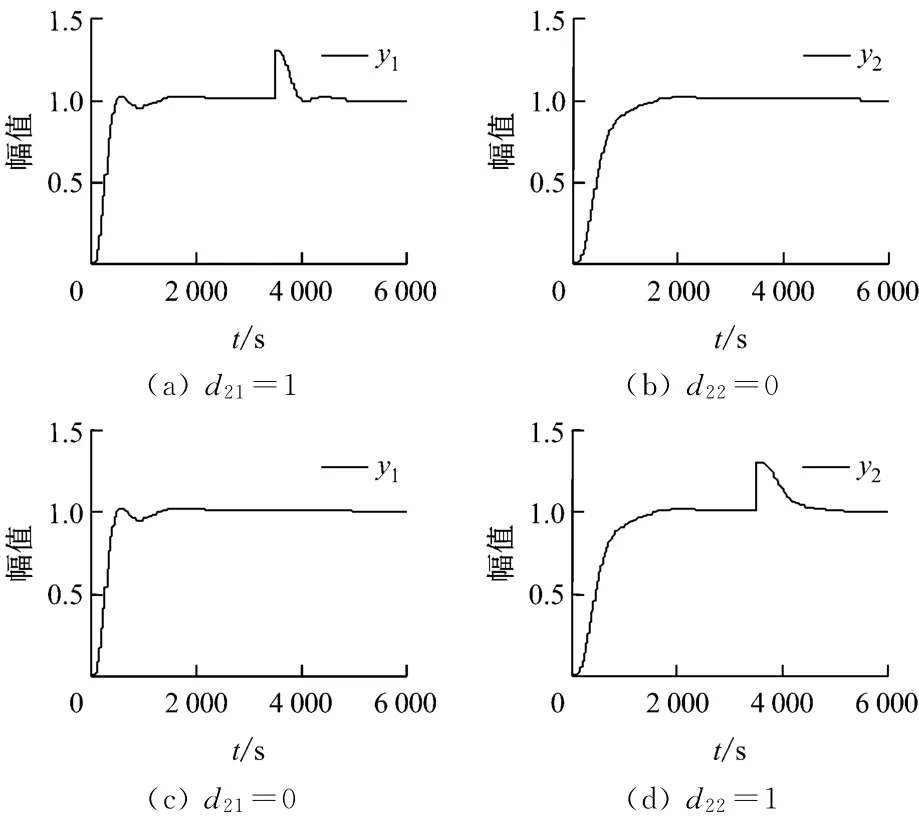
圖6 輸出擾動響應曲線Fig.6 System response under output disturbance

工業過程的復雜性決定了建模誤差難以避免.為驗證系統的魯棒性，同時將過程對象的增益減小10%、遲延減小10%、慣性時間常數增大10%，得到圖7所示模型失配時系統的響應曲線.

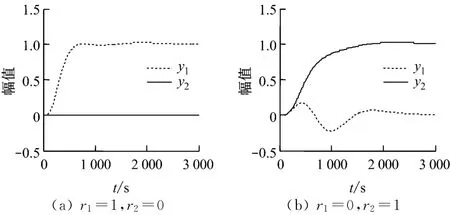
圖7 模型失配時系統的響應曲線Fig.7 Response curves in the case of model mismatch

由圖7可見，在存在一定建模誤差的情況下，系統的解耦性能和響應效果比較令人滿意.仿真發現，床溫對遲延項和慣性時間常數較敏感，響應過程出現了較長時間的小幅波動，但能夠得到有效控制.進一步研究可知，模型誤差對床溫和主蒸汽壓力的影響基本一致.在標稱系統中，主蒸汽壓力和床溫的耦合作用造成的波動大小數量級分別為10－10和10－7.在模型失配情況下，床溫的波動達到10－1，而主蒸汽壓力的波動也增大到10－4.這說明隨著模型失配加劇，系統的波動幅度成指數級增大，控制性能逐漸惡化，內模控制模型對建模精度仍有一定要求.盡管內模控制具有強魯棒性，系統最終仍能夠穩定，但對于更大的模型誤差，應考慮增強魯棒性的措施.

鑒于控制器傳遞函數的階數與控制器實際實現難度成正比，運用次最優降階方法對原控制器傳遞函數矩陣的每個元素進行模型降階.降階后的低階模型同時也能更方便地進行IMC－PID轉化，以更好地應用到工業過程分散控制系統（DCS）中.將模型降階到工業對象常見表達形式（一階＋遲延、二階＋遲延等），得到如下結果：

將該降階控制器用于對象控制，效果見圖8.由圖8可知，降階控制器對主蒸汽壓力的控制效果比較理想，給煤量對床溫的耦合作用能夠基本消除，調節的平穩性也較好，但在調節初期存在明顯負調.實際運行中，將CFB鍋爐床溫保持在最佳工作點附近即可，床溫的小幅波動對燃燒和脫硫效率的影響是可以接受且不可避免的.但應看到，降階前控制器對給煤量的控制并不存在負調，但降階前后模型的時域吻合度好于頻域吻合度，可考慮從頻域角度（如RLS方法）進行模型降階來設計低階控制器.

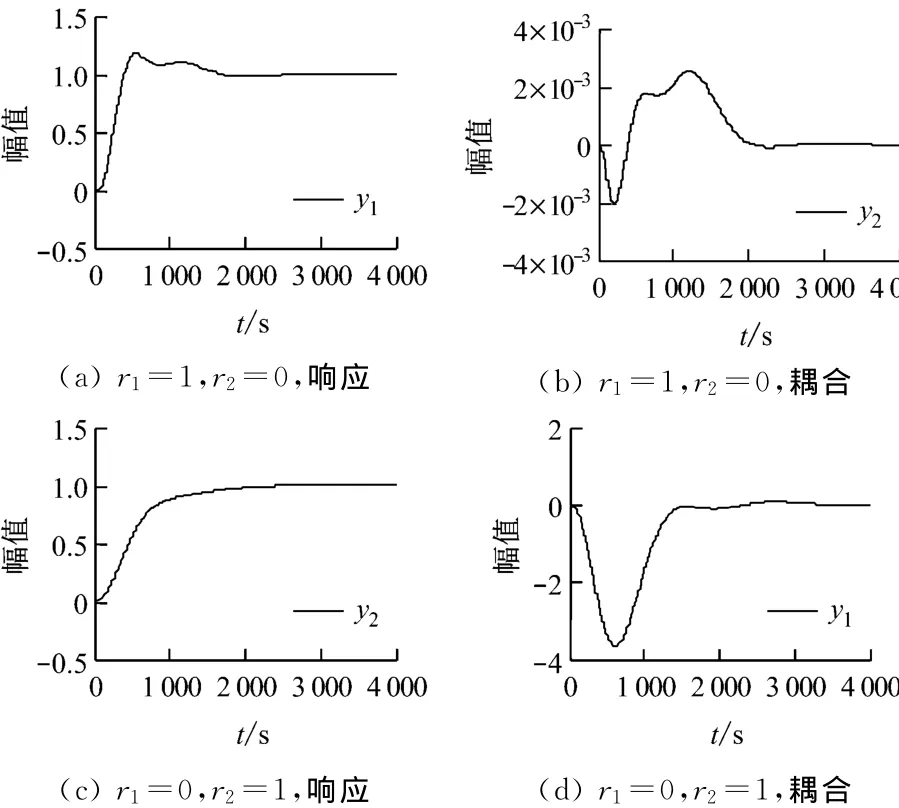
圖8 降階控制器的階躍響應曲線Fig.8 Response curves of order－reduced controllers

4 結 論

（1）通過采用解析的多變量內模解耦控制方法，有效地對CFB鍋爐中強耦合的床溫和主蒸汽壓力變量進行解耦.結果顯示，本文改進方法對輸入、輸出擾動具有良好的抑制作用，對模型誤差有較好的魯棒性.

（2）解耦中采用了次最優降階算法和遲延逼近方法，簡化了復雜的運算和控制器的實現難度.采用NLJ優化算法和改進的濾波器形式來設計控制器，在仿真中取得較好效果.

［1］胡昌華，盧嘯風.600MW超臨界循環流化床鍋爐設備與運行［M］.北京：中國電力出版社，2012.

［2］王東風，王劍東，韓璞.一種多變量系統的內模解耦控制設計方法［J］.控制工程，2003，10（5）：463－465.WANG Dongfeng，WANG Jiandong，HAN Pu.New design of internal model decoupling control for multivariable system［J］.Control Engineering of China，2003，10（5）：463－465.

［3］JIN Qibing，QUAN Ling，QI Fei，et al.Internal model control for multivariable coupling system with time delays and optimization research［C］／／Measuring Technology and Mechatronics Automation （ICMTMA），2010International Conference on IEEE.Changsha，China：IEEE Computer Society，2010：505－509.

［4］楊錫運，徐大平，張彬.再熱汽溫系統的內模解耦控制［J］.動力工程，2004，24（4）：529－532.YANG Xiyun，XU Daping，ZHANG Bin.Research on internal model control with decoupling in reheats temperature system［J］.Power Engineering，2004，24（4）：529－532.

［5］WANG Q G，ZHANG Y，CHIU M S.Decoupling internal model control for multivariable systems with multiple time delays［J］.Chemical Engineering Science，2002，57（1）：115－124.

［6］周平，柴天佑，陳通文.工業過程運行的解耦內模控制方法［J］.自動化學報，2009，35（10）：1362－1368.ZHOU Ping，CHAI Tianyou，CHEN Tongwen.Decoupling internal model control method for operation of industrial process［J］.Acta Automatica Sinica，2009，35（10）：1362－1368.

［7］CHEN J，HE Z F，QI X.A new control method for MIMO first order time delay non－square systems［J］.Journal of Process Control，2011，21（4）：538－546.

［8］靳其兵，袁琴.雙輸入雙輸出過程解耦內模控制［J］.控制工程，2009，16（1）：5－7.JIN Qibing，YUAN Qin.Decoupling internal model control for two－input two－output process［J］.Control Engineering of China，2009，16（1）：5－7.

［9］馬素霞，楊獻勇.循環流化床鍋爐燃燒系統的動態特性研究［J］.中國電機工程學報，2006，26（9）：1－6.MA Suxia，YANG Xianyong.Study on dynamic behavior of the combustion system of a circulating fluidized bed bolier［J］.Proceedings of the CSEE，2006，26（9）：1－6.

［10］NORMEY－RICO J E，BORDONS C，CAMACHO E F.Improving the robustness of dead－time compensating PI controllers［J］.Control Engineering Practice，1997，5（6）：801－810.

［11］王倫，張衛東，劉永紅.關于內外分解和譜分解問題的解析計算［J］.上海交通大學學報，2007，41（6）：889－893.WANG Lun，ZHANG Weidong，LIU Yonghong.The analytic computation of inner－outer and spectral factorization problems［J］.Journal of Shanghai Jiaotong University，2007，41（6）：889－893.

［12］ZHANG W，LIN C，OU L.Algebraic solution to H2control problems.II.the multivariable decoupling case［J］.Industrial ＆ Engineering Chemistry Research，2006，45（21）：7163－7176.

［13］陳培穎，歐林林，孫敬，等.改進的內模控制方法及其在非方系統中的應用［J］.控制與決策，2008，23（5）：581－584.CHEN Peiying，OU Linlin，SUN Jing，et al.Modified internal model control and its application in nonsquare processes［J］.Control and Design，2008，23（5）：581－584.

［14］HORN I G，ARULANDU J R，GOMBAS C J，et al.Improved filter design in internal model control［J］.Industrial ＆ Engineering Chemistry Research，1996，35（10）：3437－3441.

［15］RAO A S，CHIDAMBARAM M.Smith delay compensator for multivariable non－square systems with multiple time delays［J］.Computers ＆Chemical Engineering，2006，30（8）：1243－1255.

［16］潘立登.LJ最優化方法的改進［J］.化工自動化及儀表，1985（1）：10－15.PAN Lideng.An improvement in optimal tuning method with least performance index［J］.Control and Instruments in Chemical Industry，1985（1）：10－15.

［17］XUE D，ATHERTON D P.A suboptimal reduction algorithm for linear systems with a time delay［J］.International Journal of Control，1994，60（2）：181－196.

［18］尹先斌，周有訓.基于Taylor和Pade能逼近的滯后系統IMC－PID研究［J］.昆明理工大學學報：理工版，2006，31（2）：76－79.YIN Xianbin，ZHOU Youxun.Taylor and Pade IMC－PID［J］.Journal of Kunming University of Science and Technology：Science and Technology，2006，31（2）：76－79.