基于自適應逆控制的汽輪機調速系統研究

王萬召， 王 杰

（1.河南城建學院 能源與建筑環境工程學院，平頂山467036；2.鄭州大學 電氣工程學院，鄭州450001）

電站汽輪機調速系統是對汽輪機進行控制的主要系統，其動態性能直接影響機組的經濟性和安全性.然而調速系統內的慣性、擾動、參數時變、死區和飽和等環節使得對象特性呈現出嚴重的非線性和時變性，常規PID控制系統難以取得理想的控制效果.為克服常規PID的不足，許多研究者嘗試將智能控制方法引入PID控制，形成各種改進型PID調節系統，如模糊優化PID、神經網絡PID、遺傳算法PID等.在將上述改進型PID控制應用于汽輪機調速系統控制時，需要引入汽輪機功率信號作為負反饋信號，構成功率控制內回路，形成串級控制結構［1－3］.然而，由于汽輪機功率信號難以測量，實際應用中常用發電機功率信號代替汽輪機功率信號，但是二者對控制系統動態特性的影響差異很大［4］.筆者不再簡單沿用發電機功率信號代替汽輪機功率信號構成負反饋的控制框架，而是將發電機功率作為負荷擾動信號引入汽輪機調速系統，同時考慮到調速系統非線性和參數時變的特點，提出一種基于自適應逆控制的汽輪機調速控制系統.

自適應逆控制是由美國斯坦福大學著名教授Widrow于1986年首次提出的，其基本思想就是要用一個來自控制器的信號去驅動對象，而該控制器的傳遞函數就是該對象本身傳遞函數的逆.與傳統的反饋控制系統相比，自適應逆控制系統可以對對象給定信號的控制和對象擾動的控制分別進行自適應控制處理，使二者同時達到最優［5］.近年來，自適應逆控制技術以其自身的諸多優點成為一個活躍的研究領域，現已成為一個全新的活躍分支［6－7］.如何克服對被控對象精確模型解析式的依賴，實現在線辨識得到實際對象動態特性控制的逆控制器和對象擾動抑制的擾動消除控制器，是自適應逆控制方案走向實用的關鍵.

筆者首先利用徑向基函數（Radial Basis Function，RBF）神經網絡在線辨識獲得汽輪機調速系統的逆模型，作為逆控制器構成自適應逆控制系統，實現動態特性的控制；然后利用RBF神經網絡在線辨識獲得一個自適應對象擾動消除器，實現對象擾動消除控制.最后，利用仿真實例驗證該方案的可行性和有效性.

1 汽輪機調速對象特性分析

在工程實際中，由于汽輪機功率信號難以測量，而發電機功率信號容易測量.考慮到二者對系統動態特性的影響差別很大，筆者不再簡單使用發電機功率信號代替汽輪機功率信號作為負反饋信號構成功率內回路.當把發電機信號作為負荷擾動信號處理時，汽輪機調速系統動態特性方框圖如圖1虛線框內所示.圖1中對調速對象進行了簡化處理，沒有表示出各單元中的慣性、滯后和非線性特性，均采用簡化的線性單元表示.相關參數意義如下：Ty為電液轉換器時間常數；Tc為油動機時間常數；Tv為蒸汽容積時間常數；Tr為再熱器時間常數；Ta為轉子時間常數；Ch、Cm、Cd分別為高、中、低壓缸傳遞函數的比例系數.

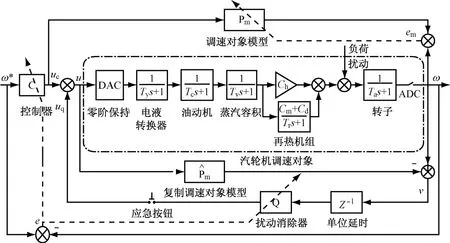
圖1 汽輪機調速系統自適應逆控制結構圖Fig.1 Block diagram of the turbine speed governing system based on adaptive inverse control

2 汽輪機調速系統自適應逆控制

自適應逆控制將被控對象的逆模型作為控制器，對被控對象的動態特性進行開環控制，使對象的輸出跟蹤給定信號變化.被控對象的逆模型（即自適應控制器）可利用自適應算法在線辨識獲得，反饋僅在該逆控制器參數的自適應過程中采用，不參與系統動態特性的控制過程.由于跟蹤給定信號控制中沒有從輸出到輸入的反饋，就會讓對象內部噪聲和外部擾動毫無抑制地出現在對象的輸出端，為此需要設計一個擾動消除控制器.由于汽輪機調速對象具有嚴重的非線性和參數時變性，為取得良好的控制效果，給定信號跟蹤控制器和擾動消除控制器都需要采用在線辨識方法獲得.因此，根據自適應逆控制的基本理論，提出汽輪機調速自適應逆控制系統結構（見圖1）.圖1中，C為動態特性控制器（即對象逆模型）；Q為擾動消除控制器；uc、uq分別為C和Q的輸出；u為對象實際輸入.

2.1 汽輪機調速對象模型的在線辨識

汽輪機調速對象是具有死區、慣性和參數時變的非線性對象，其差分方程可表示為

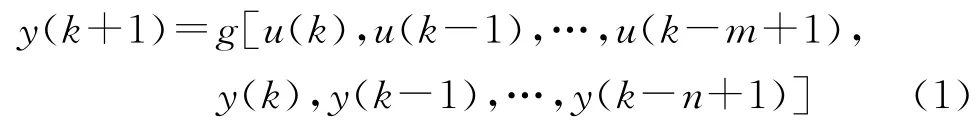
式中：u和y分別為汽輪機調速對象的控制輸入信號和汽輪機輸出轉速；m和n分別為輸入、輸出對應階次.

為實現汽輪機調速對象這種非線性時變對象模型的在線辨識，筆者選用RBF神經網絡作為辨識工具.RBF神經網絡［8］是一種局部逼近網絡，已證明它能以任意精度逼近任意連續函數，多輸入單輸出RBF神經網絡結構見圖2.

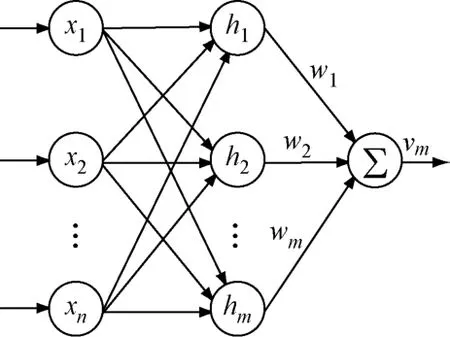
圖2 多輸入單輸出RBF神經網絡結構Fig.2 Structure of the multi－input single－output RBF neural network

圖2中，hj為高斯基函數，即

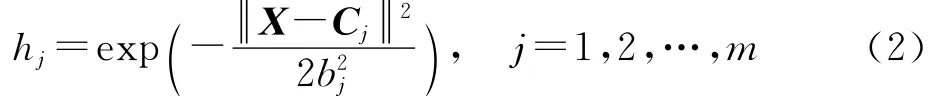
關于RBF神經網絡更詳細的描述可參考文獻［8］，此處不再贅述.

根據圖1中對汽輪機調速對象模型Pm辨識結構的要求，可確定RBF神經網絡1的輸入層為

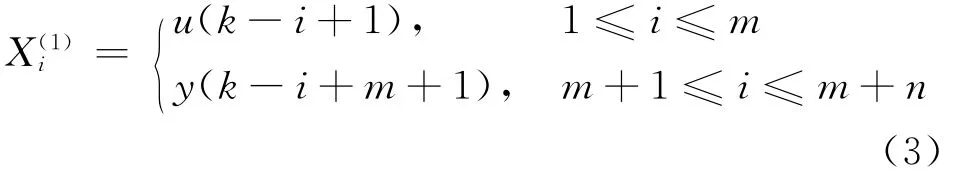
該模型辨識RBF神經網絡1輸出層的輸出為ym（k＋1）.取辨識指標為

根據梯度下降法，權值的修正公式如下：

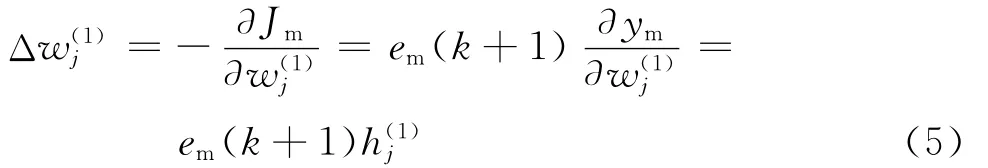
由于RBF神經網絡輸入向量的第一個分量為u（k），可得汽輪機調速對象的Jacobian信息為

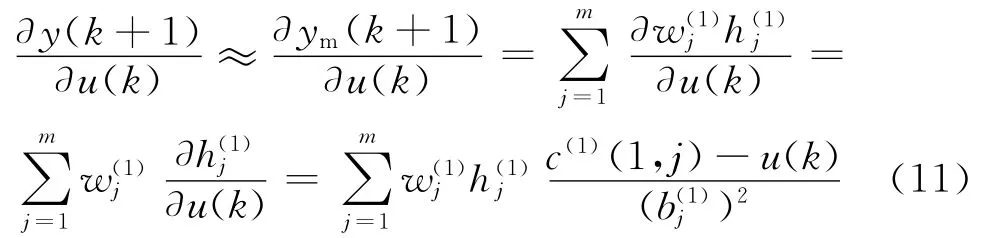
式中：η（1）為 RBF 神 經 網 絡 1 的 學 習 速 率；α（1）為RBF神經網絡1的動量因子.

代表對象輸出對輸入靈敏度的Jacobian信息將在隨后自適應逆控制器和擾動消除控制器的在線辨識算法中用到.

2.2 汽輪機調速對象逆模型的在線辨識

汽輪機調速對象在滿足可逆的條件下，其對應逆模型的差分方程可表示為

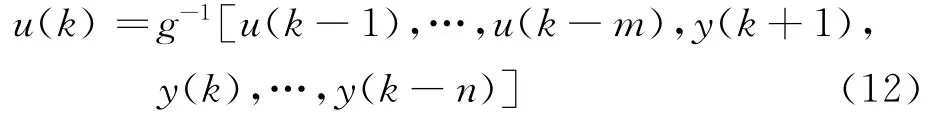
根據圖1自適應逆控制器（即對象逆模型）學習算法的任務要求，RBF神經網絡2的輸入層為

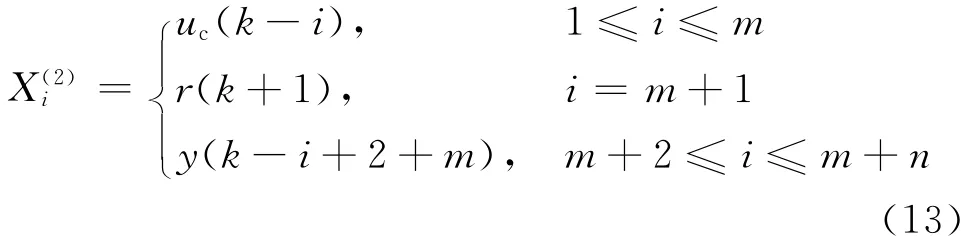
其中r（k＋1）表示下一時刻的轉速指令信號.RBF神經網絡2的輸出層的輸出為uc（k）.取辨識指標為

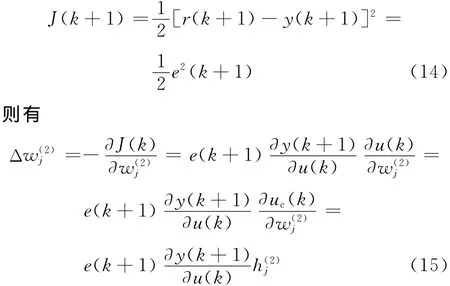
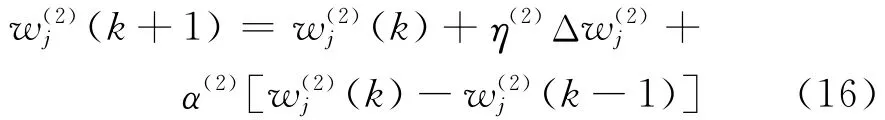
同理可得權值的修正公式如下

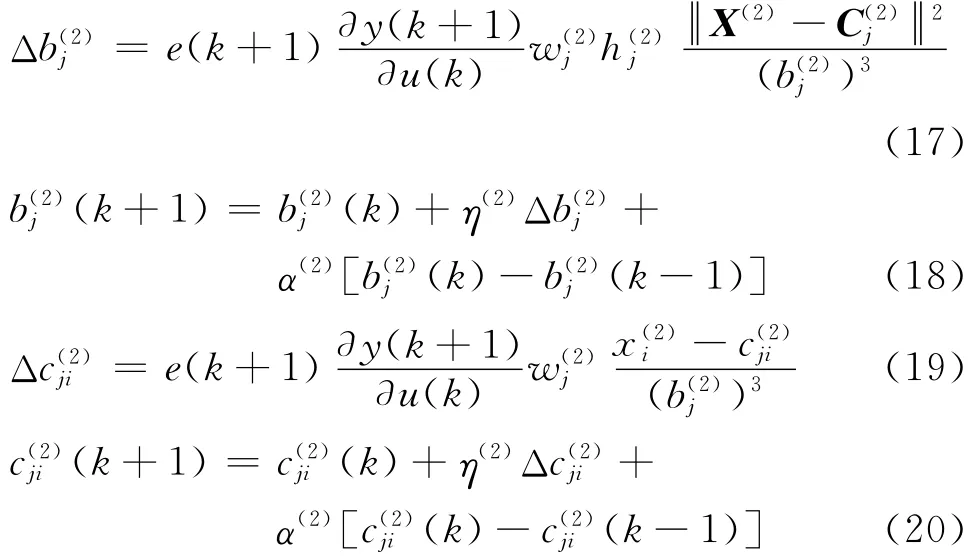
式中：η（2）為 RBF 神 經 網 絡2 的 學 習 速 率；α（2）為RBF神經網絡2的動量因子.

2.3 調速系統擾動消除控制器的在線辨識

汽輪機調速系統完成對象擾動消除是這樣進行的：控制信號u同時作用到復制的對象模型（非常接近無擾動的對象）和對象P，對兩者的輸出求差可以將擾動信號引起的效果（即等效擾動v）分離出來，然后針對等效擾動v在線構建自適應的擾動消除控制器，來消除該擾動作用.考慮到數字反饋鏈路在環繞每一個回路上都必須至少有一個單位的延時，所以在擾動消除控制器Q前布置一個單位延時環節.于是，擾動消除控制器所對應的差分方程可表示為

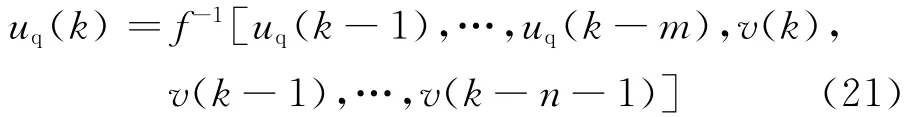
采用RBF神經網絡3來在線辨識獲得擾動消除控制器.RBF神經網絡3的輸入層為

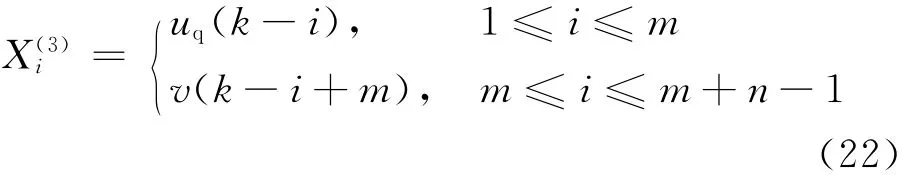
取性能指標為

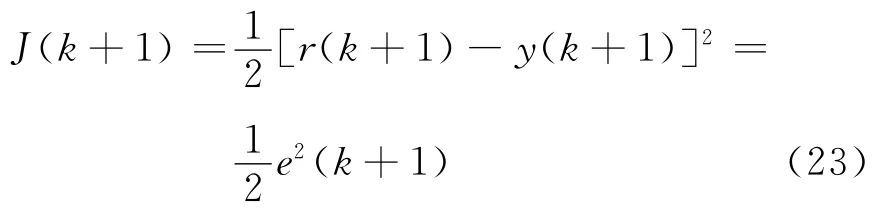
則有

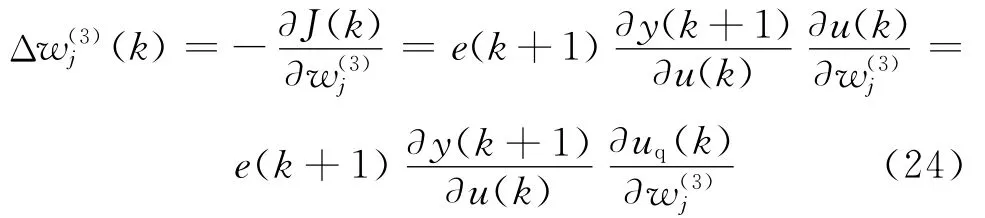
利用對象的Jacobian信息，采用梯度下降法，可得RBF神經網絡3的權值修正公式如下

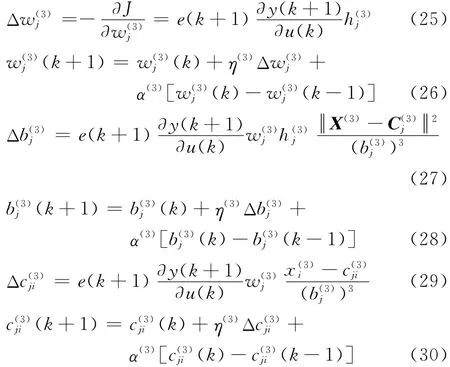
式中：η（3）為 RBF 神 經 網 絡 3 的 學 習 速 率；α（3）為RBF神經網絡3的動量因子.

考慮到等效擾動v的分離過程，要求在閉合擾動消除回路前確保對象模型收斂并接近對象P，此時調速對象輸出和模型輸出的差值em接近0.在系統運行中，當該條件被破壞時，必須利用應急按鈕切除擾動消除器，直到滿足該條件，才能再次投運擾動消除控制器.

3 仿真實驗及分析

為驗證所提出的汽輪機調速系統自適應逆控制策略的有效性和可靠性，對文獻［9］中東北電網某電廠200MW機組汽輪機調速系統進行仿真研究.調速系統對象參數取如下典型值：Ty＝0.01s，Tc＝0.084s，Tv＝0.345 5s，Ta＝8s，Tr＝8s，Ch＝1，Cm＝0.5，Cd＝0.5，采樣時間Ts取2s.

3.1 汽輪機轉速指令跟蹤工況仿真

為檢驗控制系統輸出跟蹤轉速指令信號的性能，在轉速指令信號輸入端加入階躍信號，考察系統輸出跟蹤給定轉速信號的快速性和準確性.為進行比較，對處于文獻［9］典型參數值下的調速對象同時進行傳統PID控制仿真，PID控制器參數也取文獻［9］中推薦的值，即kp＝0.23，ki＝0.5，kd＝0.1.轉速指令階躍變化時系統的輸出響應仿真結果見圖3.由圖3可以看出，傳統的PID控制調節時間長、超調量大、振蕩大；而筆者提出的自適應逆控制方案可以在汽輪機轉速指令信號階躍變化時實現快速、精確跟蹤，穩定性好、無超調、調節時間短、控制品質良好.自適應逆控制方案中汽輪機調速對象逆模型辨識器RBF神經網絡2的學習速率取0.02，動量因子取0.01，調速對象模型辨識器RBF神經網絡1的學習速率取0.1，動量因子取0.01.圖4給出了汽輪機調速對象在該工況下的Jacobian信息辨識結果，顯示了對象辨識器RBF神經網絡1在線實時學習調速對象動態特性的過程.

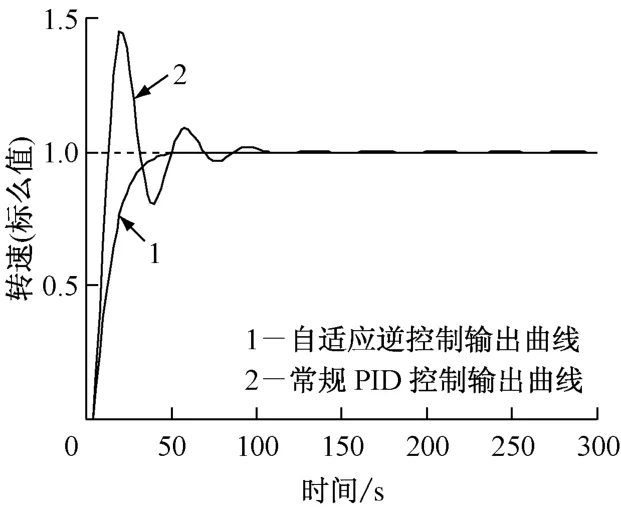
圖3 轉速指令階躍變化時系統的輸出響應Fig.3 System output response to step change of rotating speed instruction

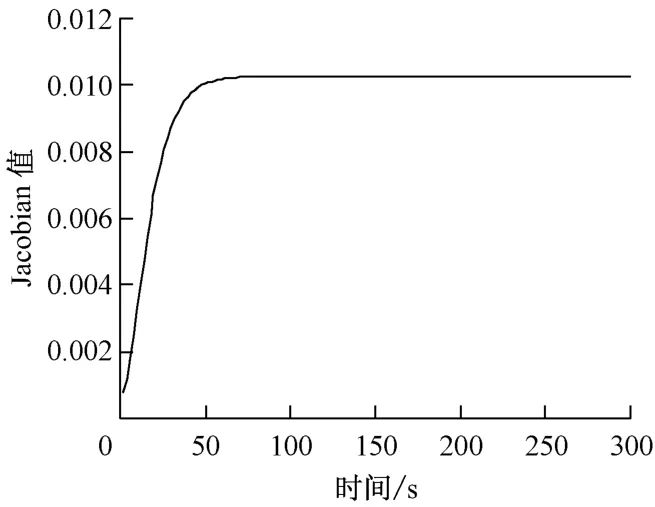
圖4 汽輪機調速控制系統Jacobian信息辨識結果Fig.4 Jacobian information identification for the turbine speed governing system

3.2 汽輪機擾動消除工況仿真

為檢驗自適應擾動消除控制器對擾動信號的抑制效果，在實施轉速指令控制的自適應逆控制器穩定工作后，對系統施加圖5所示的方波形式的負荷擾動信號，分別對擾動消除控制器未投入和投入工況進行仿真實驗，結果示于圖6和圖7.對比圖6和圖7可知，在系統面臨外部（或負荷）擾動時，除擾動信號剛加入時由于擾動消除控制器需進行自適應學習過程，使得擾動效果幅度稍大之外，在隨后的過程中，擾動效果的持續時間都大幅縮短，顯示出良好的擾動抑制效果.其中，擾動消除控制器RBF神經網絡3的學習速率取0.05，動量因子取0.1.

圖5 外部負荷擾動信號Fig.5 External load disturbance signal

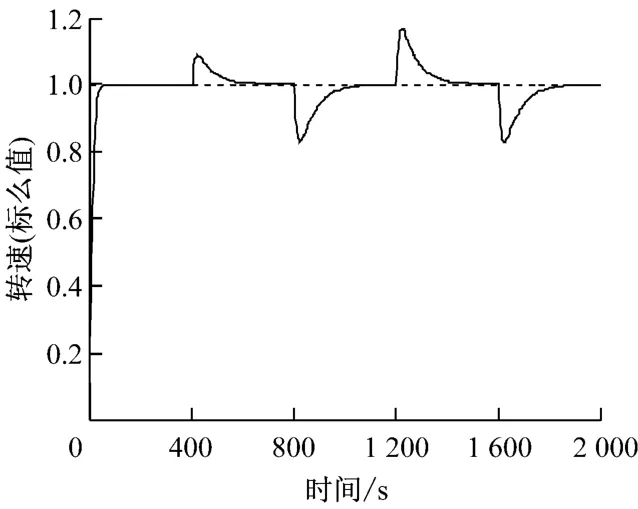
圖6 擾動消除控制器未投運時系統輸出響應Fig.6 System output response without disturbance canceller

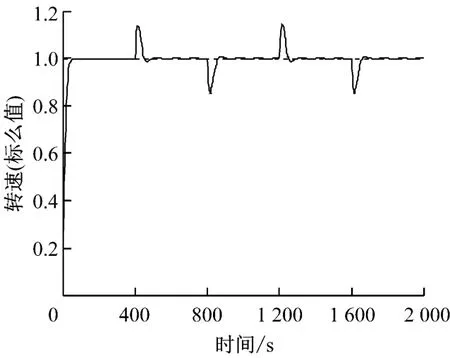
圖7 擾動消除控制器投運時系統輸出響應Fig.7 System output response with disturbance canceller

4 結 論

基于自適應逆控制的基本思想，提出一種汽輪機調速系統自適應逆控制算法，將該算法應用于某200MW機組汽輪機調速系統并進行仿真實驗，結果表明：與PID汽輪機調速控制方案相比，所提出的汽輪機調速系統自適應逆控制算法不僅能夠很好地跟蹤速度指令，而且能夠有效抑制擾動響應，控制品質優良，具有很強的魯棒性.筆者所提出的算法具有一般性，為大慣性、參數時變、外擾大、難于精確建模的非線性對象的控制提供了一種新的解決方案.

［1］王爽心，王印松，朱衡君.汽輪機調速系統模糊控制的研究［J］.系統仿真學報，2005，17（9）：2196－2198.WANG Shuangxin，WANG Yinsong，ZHU Hengjun.Research on fuzzy control of turbine regulating system［J］.Journal of System Simulation，2005，17（9）：2196－2198.

［2］范鑫，秦建明，李明，等.超臨界600MW汽輪機運行方式的優化研究［J］.動力工程學報，2012，32（5）：356－361.FAN Xin，QIN Jianming，LI Ming，et al.Study on operation mode optimization for a 600MW supercritical steam turbine［J］.Journal of Chinese Society of Power Engineering，2012，32（5）：356－361.

［3］王爽心，姜妍，李亞光.基于混合混沌優化策略的汽輪機調速系統模糊免疫PID控制 ［J］.中國電機工程學報，2006，26（11）：70－74.WANG Shuangxin，JIANG Yan，LI Yaguang.Fuzzyimmune－PID control of the turbine governing system based on compound chaos optimization strategy ［J］.Proceedings of the CSEE，2006，26（11）：70－74.

［4］王爽心，葛曉霞.汽輪機數字電液控制系統 ［M］.北京：中國電力出版社，2004.

［5］WIDROW B，WALACH E.Adaptive inverse control［M］.New Jersey：Prentice Hall，1996.

［6］曲永印，白晶，周振雄，等.自適應逆控制的異步電機變頻調速系統研究［J］.控制與決策，2007，22（7）：821－824.QU Yongyin，BAI Jing，ZHOU Zhenxiong，et al.A－daptive inverse control variable frequency speed regulation of asynchronous motor［J］.Control and Decision，2007，22（7）：821－824.

［7］WIDROW B，PLETT G L，FERREIRA E.Adaptive inverse control based on nonlinear adaptive filtering［C］／／Proc.5th IFAC Workshop Algorithms Architectures for Real－Time Control.Cancun，Mexico：International Federation of Automatic Control by Pergamon，1998：247－252.

［8］劉金琨.智能控制［M］.北京：電子工業出版社，2005.

［9］王志群，朱守真，樓鴻祥，等.基于時域分段線性多項式法的大型汽輪機建模和參數辨識［J］.中國電機工程學報，2003，23（4）：128－133.WANG Zhiqun，ZHU Shouzhen，LOU Hongxiang，et al.PLPF based modeling and parameter－identifying of large system turbine in time domain［J］.Proceedings of the CSEE，2003，23（4）：128－133.