一種利用高斯函數的聚類算法

王祥斌，楊 柳，鄧倫治

(貴州師范大學數學與計算機科學學院，貴州貴陽550001)

0 引言

所謂聚類就是把一組個體按照相似性歸納成若干類別，即將數據集劃分成若干個簇，使得同一個簇中的對象具有較高的鄰近度(相似性)，可以將簇中的數據對象作為一個整體來對待與使用，而簇與簇之間的對象鄰近度(相似性)較低[1-4］。

許多聚類算法都在試圖尋找一種很好的途徑，來實現對大規模數據集進行聚類分析時獲得理想的效果，但是都在一定的程度上存在著局限性。例如，經典的基于劃分的k均值聚類算法(k-means)而言，需要事先給定出簇的數量，而且還只能發現超球狀簇，這在很大程度上影響了此種聚類分析的準確性[5-6］。基于密度的聚類算法，因為其采用以數據集在某空間區域的稀疏程度來作為發現簇的依據，能夠自動而非人為給定簇的數量，因此，能夠發現任何形狀的簇，越來越得到業界的關注。本文從傳統的基于密度的帶噪音的空間數據聚類算法(DBSCAN)入手，提出了一種改進的基于密度分布函數的聚類算法，繼而給出相關算法的概念定義，重點是利用高斯函數來描述數據對象之間親疏程度，最后，利用Iris數據集進行了相應的試驗。試驗結果證明:該算法能有效地提高聚類的效率。

1 傳統的密度聚類—DBSCAN

傳統的DBSCAN算法，其中心思想就是要在數據集中尋找被低密度區所分割出來的高密度局域，進而由所獲得的高密度區的分布狀況，就可以確定出結果中簇的數量。在此基礎上，下文給出改進算法時需要用到的幾個概念的定義[7-9］。

定義1 鄰域:給定數據集D的一個任意對象p，p的鄰域定義為以p點為圓心，以Eps為半徑的圓內包含的所有點的集合，記為NEps(p)，即其中，dist(p，q)表示D中兩個對象p和q之間的距離。

定義2 密度:數據集D中某一對象p的鄰域內所包含的點的數目稱為該點p的密度，記為

定義3 核心點與非核心點:對于對象p∈D，給定一個密度閾值MinPts(MinPts∈Z)。如果有則稱對象p為(Eps，MinPts)條件下的核心點，記為point_core;反之稱為非核心點，記為non_point_core。

定義4 直接密度可達:給定(Eps，MinPts)，如果對象p和q滿足MinPts，則稱對象p從對象q直接密度可達。

定義5 類:數據集D的非空集合C是一個類，當且僅當C滿足如下條件:

(Ⅰ)對于數據集中的任意點p和q，若p∈C且q從p密度可達，則q∈C。

(Ⅱ)對于數據集中的任意點p和q，如果有p∈C和q∈C，則p和q是密度連接的。

在以上的敘述中，定義1～定義3確立了關于密度的概念。DBSCAN算法中以(Eps，MinPts)作為算法的參數確定一個密度閾值，把密度大于MinPts的對象視為核心點。在對數據集D進行一次掃描之后，確定出所有的核心點，所有密度可達的核心點即可以被合并成為簇，而邊界點劃歸至最近的簇。不是核心點或者邊界點的對象被視為噪聲。值得注意的是，由于算法采用的是密度可達而不是中心距離的概念，所以DBSCAN所獲得的簇可以是任意形狀的。

DBSCAN算法也有著薄弱的方面，該算法對于密度區域反差較大的數據集的處理能力比較理想，但是對于密度區域反差不明顯的數據集處理則不盡如人意。而面對密度區域反差不明顯的數據集進行聚類的情況下，如何給定出合適的MinPts參數值比較困難。

2 改進的利用高斯函數的聚類(Gause-DBSCAN)

聚類分析算法按照對象在性質上的親疏遠近進行分類。為了使分類的結果比較合理，必須描述對象之間的親疏遠近的程度。這種親疏遠近的程度稱之為鄰近度(相似性)。通常地，描述對象之間的鄰近度主要有距離和相似系數兩個方面。目前，常用的對象鄰近度度量的方法包括歐幾里德距離、余弦相似性、Jaccard相似性、共享最近鄰相似性(SNN)等[10-11］。

Gause-DBSCAN算法是在DBSCAN算法的基礎上，對其進行改造。最大的特點是在算法中引入了密度分布函數的概念，并且采用了高斯函數來描述對象之間親疏程度。

定義6 給定數據集D中的對象p和q，且q對p的影響函數記為:ρ(p，q)。該函數是由p和q之間的距離來決定的，這個距離的描述，采用了高斯函數。于是有

進一步地，給定k個數據對象D=(x1，x2，…，xk)，可在數據對象p上定義出數據對象p的密度函數，即所有數據點的影響函數之和，記為Density(p)，則有

其中，dist(p，i)是數據對象p和第i個近鄰之間的歐氏距離。距離越小，意味著該對象的鄰域越緊湊，密度自然也就越大。

算法思想:

步驟1:預處理數據集D。

步驟2:設定一個密度閾值MinPts和Eps，計算出每一個數據對象的密度，從而可以確定哪些對象是point_core，將這些數據對象存入隊列point_core_queue。

步驟3:檢查找出的所有point_core中是否存在相同的數據對象。若有的話，則只保留一個作為point_core。

步驟4:以隊列point_core_queue中的point_core為種子位置，在Eps半徑范圍內，尋找其K最鄰近結點(KNN)，將找到的KNN加入至一個候選隊列candidate_queue中。

步驟5:檢查候選隊列 candidate_queue。如果隊列中出現某點 p，其密度函數滿足條件Density(p)≥Density(point_core)×MinPts，則點p成為可能目標對象。

步驟6:若p不存在于point_core_queue隊列中，則說明p與當前的point_core密切程度高，可以聚類;將該點p的KNN加入至隊列candidate_queue，再次判斷找到的新點密度函數滿足條件Density(p)≥Density(point_core)×MinPts，直到無法擴展隊列candidate_queue的成員為止。

步驟7:若p存在于point_core_queue隊列中，則將p對應的點在point_core_queue做一個訪問標記，使其不會再作為種子被訪問到。同時將p歸入當前找到的聚類中。

步驟8:當找到的點密度下降到核心點密度的密度閾值MinPts時，完成一輪搜索。反復執行步驟5～步驟7，直到候選隊列candidate_queue為空結束。

步驟9:從隊列point_core_queue中取出下一個point_core。反復執行步驟4～步驟8，直到隊列point_core_queue為空結束，即該算法完成。

3 測試及評價

對算法Gause-DBSCAN的性能進行測試，并將測試結果與常見的聚類算法進行比較。算法測試是在一臺普通PC機上進行的。該機器的配置為DualCore AMD Athlon 64 X2 5000+CPU，內存2 G、500 G硬盤，算法采用C#語言編程環境實現。測試數據集使用了Iris數據集(也稱鳶尾花卉數據集)。Iris數據集是150個關于3種鳶尾花的生物統計數據[12-13］。試驗結果如表1所示。

表1 Gause-DBSCAN聚類試驗結果

兩種算法的執行效果如圖1和圖2所示，兩種算法的效率比較見圖3。

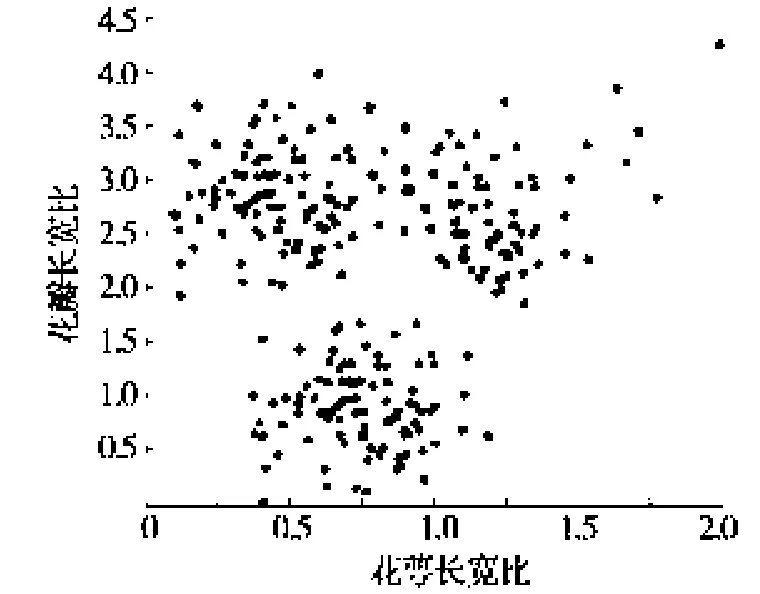
圖1 DBSCAN試驗結果

圖2 Gause-DBSCAN試驗結果

傳統的DBSCAN算法對具有N個點的數據集，其算法的時間復雜度為O(N2);在建立空間索引的情況下，其復雜度為 O(NlogN)[5］。而改進后的 Gause-DBSCAN算法因為其鄰域查詢的時間復雜度遠小于O(NlogN)，因此算法總體的時間復雜度也小于O(NlogN)。以上的試驗結果也表明:改進后的Gause-DBSCAN算法的執行效率要高于傳統的DBSCAN算法。

圖3 兩種算法執行效率的試驗結果

4 結束語

聚類是研究數據挖掘算法的重要方面之一。在研究傳統的DBSCAN算法的基礎上，本文提出了一種改進的同樣基于密度的聚類算法Gause-DBSCAN。算法從最高密度的對象著手，考察周圍對象的密度分布狀況，為了提高準確性，引入了影響函數和密度函數的概念。并在此基礎上進行了數據試驗，試驗結果表明本算法可以實現較好的聚類效果和效率。今后的工作是研究如何更加合理的設定(Eps，MinPts)這兩個參數的值，并且研究如何進一步縮短算法的執行時間。

[1]Mac Q J.Some Methods for Classification and Analysis of Multivariate Observations[C］∥Proc of Fifth BerkeleySymposium on Math.Stat and Prob:University of California Press，1967:281-297.

[2]Christian M，Diem H.Clustering by Kernel Density[J］.Computational Economics，2007，29(2):199-212.

[3]Nasibov E N，Ulutagay G.Robustness of Density-based Clustering Methods with Various Neighborhood Relations[J］.Fuzzy Sets and Systems，2009，160(24):3601-3615.

[4]于永玲，李向，宗思生.考慮空間格局的譜聚類算法及其應用[J］.河南科技大學學報:自然科學版，2013，34(5):101-104.

[5]Tan P N，Steinbach M.數據挖掘導論[M］.范明，范宏建，譯.北京:人民郵電出版社，2006.

[6]Bicici E，Yuret D.Locally Scaled Density Based Clustering[C］//The 8th International Conference on Adaptive and Natural Computing Algorithms.Berlin:Springer-Verlag，2007:739-748.

[7]Parsons L，Haque E，Liu H.Subspace Clustering for High Dimensional Data:A Review[J］.Sigkdd Explorations，2004，6(1):90-105.

[8]趙杰，楊柳.聚類分析算法DBSCAN的改進與實現[J］.微電子學與計算機，2009，26(11):189-192.

[9]許虎寅，王治和.一種改進的基于密度的聚類算法[J］.微電子學與計算機，2012，29(2):44-46.

[10]Zhou S G，Zhou A Y，Jin W.Fdbscan:A Fast Dbscan Algorithm[J］.Journal of Software，2000，11(6):735-744.

[11]Chen N，Chen A，Zhou L X.An Incremental Grid Density Based Clustering Algorithm[J］.Journal of Software，2002，13(1):1-7.

[12]Iris Data Set(UCI)[DB/OL］.[2012-09-10］.http://www.datatang.com/data/551.

[13]張琳，陳燕，汲業，等.一種基于密度的K-means算法研究[J］.計算機應用研究，2011，28(11):4071-4085.