電子表格在電子散熱數值求解中的應用

彭 夷，張小明

(南京工業職業技術學院 能源與電氣工程學院，江蘇 南京 210023)

引言

隨著電子科技的發展，電子器件的功率密度在不斷上升。在電子設備中，良好的熱設計直接成為電子產品性能的決定因素之一。然而，在熱設計中散熱器的設計又是一個重點。因此如何用更加快捷方便的方法獲得所設計散熱器的溫度特性成為設計工程師討論的焦點問題。根據電子散熱的特性，許多散熱器可以簡化成二維傳熱問題來進行分析。對于二維穩態或瞬態傳熱問題，工程上有許多有效的方法求解這樣的傳熱問題。主要有兩類方法，一是工程圖解法，二是商業軟件仿真分析法［1，2］。工程圖解法能夠獲得比較近似的結果，其相對于商業軟件仿真分析法，誤差比較大。隨著計算機技術的發展，商業軟件仿真分析法使用頻率越來越高，但是，這種方法需要非常專業的人員去完成。對于工程中比較簡單的，形狀規則的二維傳熱問題，電子表格能更加快捷方便地利用有限差分法(FDM，Finite Difference Method)獲得所需要的相對準確的結果。

1 二維傳熱的有限差分法(Finite Difference Method，FDM)

有限差分法的根本就是將所研究的物體劃分成有限個小長方形的元素［3］，同時，假設每一個小長方形是等溫體，每個小長方形的中心成為節點或網格點。圖1就是這樣的一個網格，用整數下標來表示每一個小長方下元素的位置。

圖1 有限差分法的基本模型

在該圖中，陰影區域表示任一基本元素，是一溫度為Tm，n的等溫體，而且其邊界位于相鄰節點的中心位置。所以，根據導數的定義，可以得出

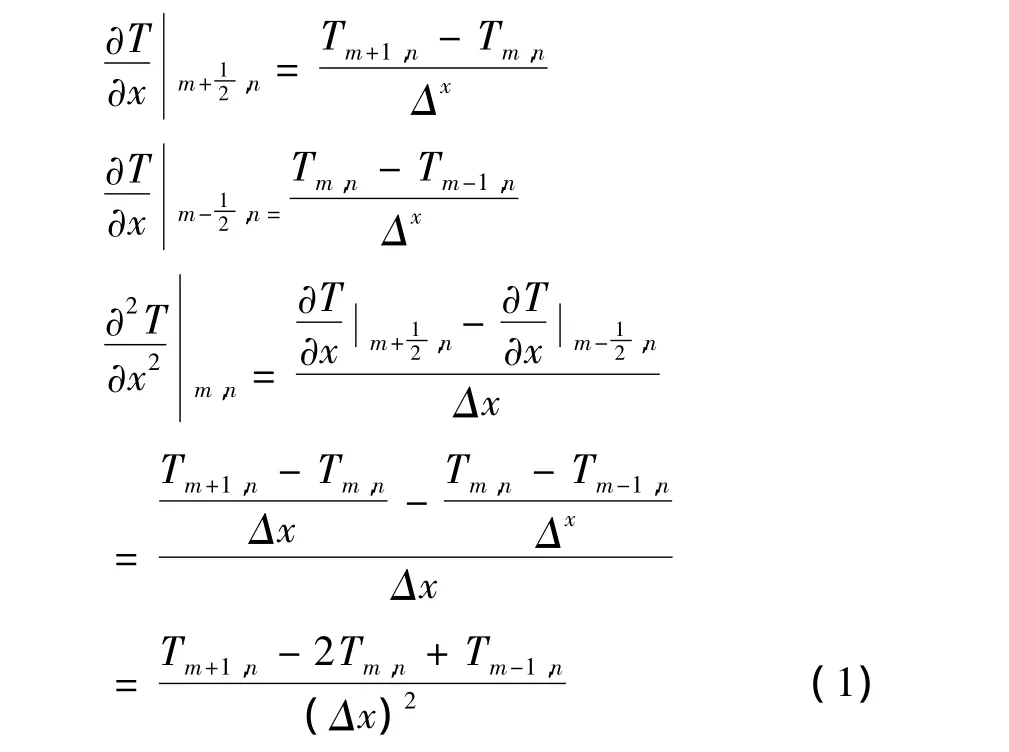
同理，對垂直方向也應有，

對于一個二維矩形物體，如果其四邊均保持不同溫度值的常數，且無內熱源，物體的導熱系數為常數。那么根據傳熱學，二維導熱問題的通用傳熱方程可以寫成，

該方程是一齊次的關于溫度T的拉普拉斯方程，如按照嚴格數學方法來求解，比較麻煩。如果采用有限差分的方法，問題就變得簡單了。將式(1)和(2)代入(3)，得到:

由式(4)可以看出，在有限差分法中溫度Tm，n實際是周邊四個節點溫度的平均值。對于求解這樣的方程，代數的方法就是列出方程組，再通過高斯 －賽德爾法去迭代，然后獲得最終的解［3-5］。為了簡化計算的過程，電子表格能夠被用來實現這樣迭代的功能，而獲得我們需要的結果。

2 二維導熱有限差分法算例

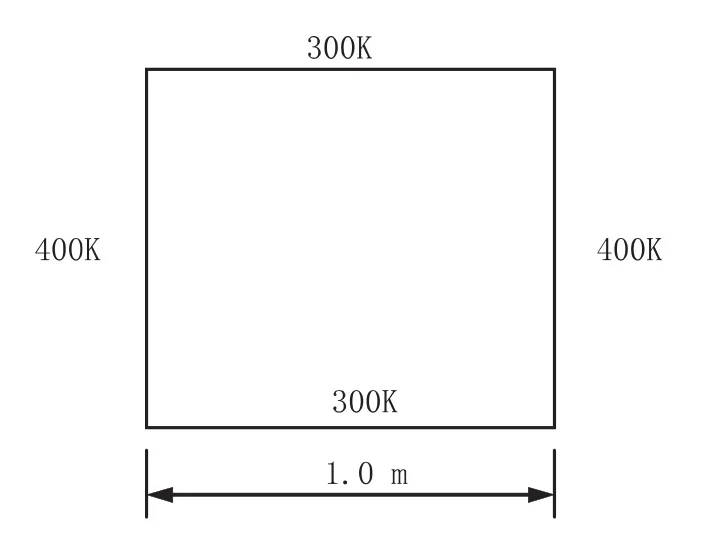
圖2 1.0 ×1.0m 金屬板

問題描述:如有一塊導熱系數為8W/mK的方形金屬板，邊長是1m。四邊溫度如圖2所示。確定在其達到熱穩定時金屬板的溫度分布。通過有限差分法，將整個金屬板劃分為100個0.1x0.1m小正方形作為基本元素，并且假設每個小正方形的溫度是均一的。用電子表格來表示如圖3所示，表格表示初始計算狀態，而且電子表格非常形象而且生動地表示出了該金屬板分成的網格狀態。圖3中陰影區域中表示金屬板中間部分單元格，每個單元格被看成一個均勻的等溫體，四周表示金屬板的溫度場邊界條件。對于單元B8，根據方程(4)其溫度值應為

以此類推，將圖3中陰影區域中的單元格中的數學關系復制到其余單元格。

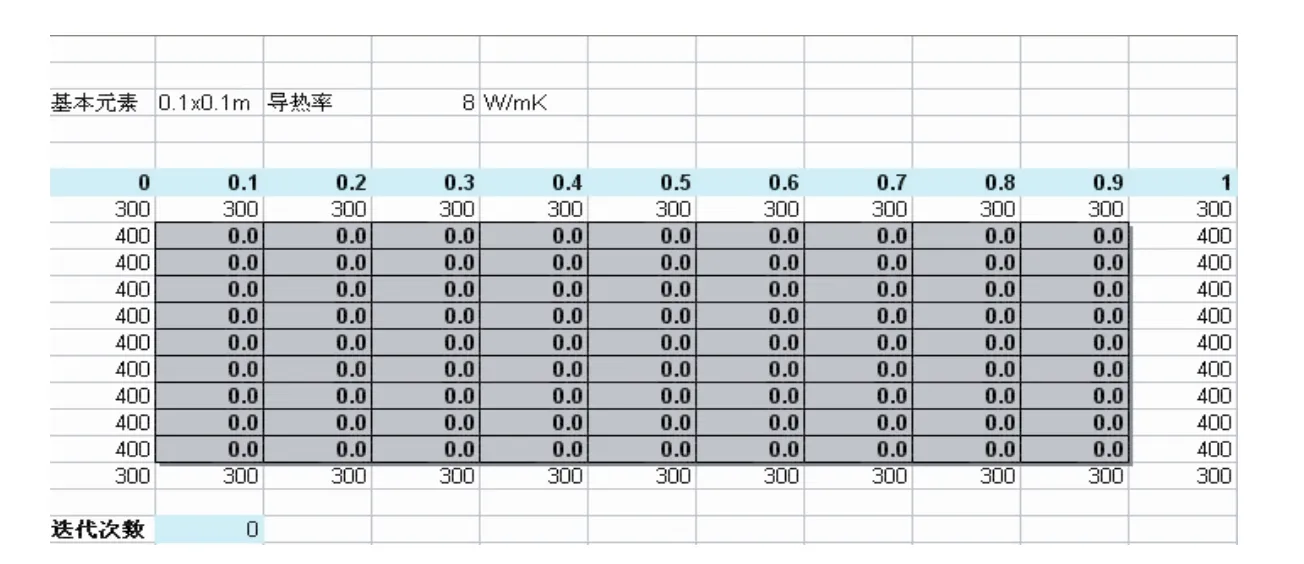
圖3 電子表格計算開始的狀態

此時，已經完成了金屬板有限差分法的網格劃分與邊界條件及初始條件的設定。下一步將設定迭代計算次數與殘差的設定。在電子表格，工具欄下選擇“選項”，并選擇“重新計算”的標簽，計算相關設定的對話框出現。選擇“手動重算”，同時勾選“迭代計算”，并設定迭代次數和最大誤差。然后，單擊F9執行計算［6］。圖4是經過11次迭代后每個單元格差分結果，通過仔細觀察可以發現單元格中的值不完全是周邊四個單元格數值之和的四分之一，這是因為這些數據是計算過程中得出的，整個代數方程組還沒有收斂而造成的。然而，圖5中反映出的數據就基本上滿足式(4)，由此可見經過100次的迭代后，整個計算基本收斂。關于這一點，可以從圖6得到驗證。而且，仔細觀察圖5中的數據會發現所有數據基本呈對稱分布，這主要是由于邊界條件是對稱的，圖7更加直觀地反映了這一特征。

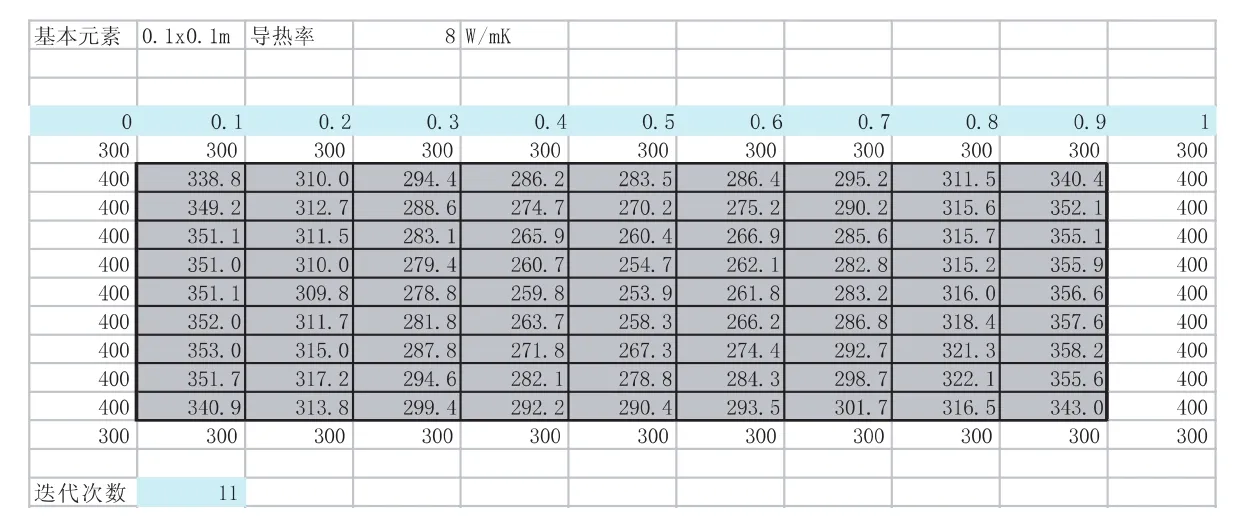
圖4 迭代11次后各單元格的溫度計算值

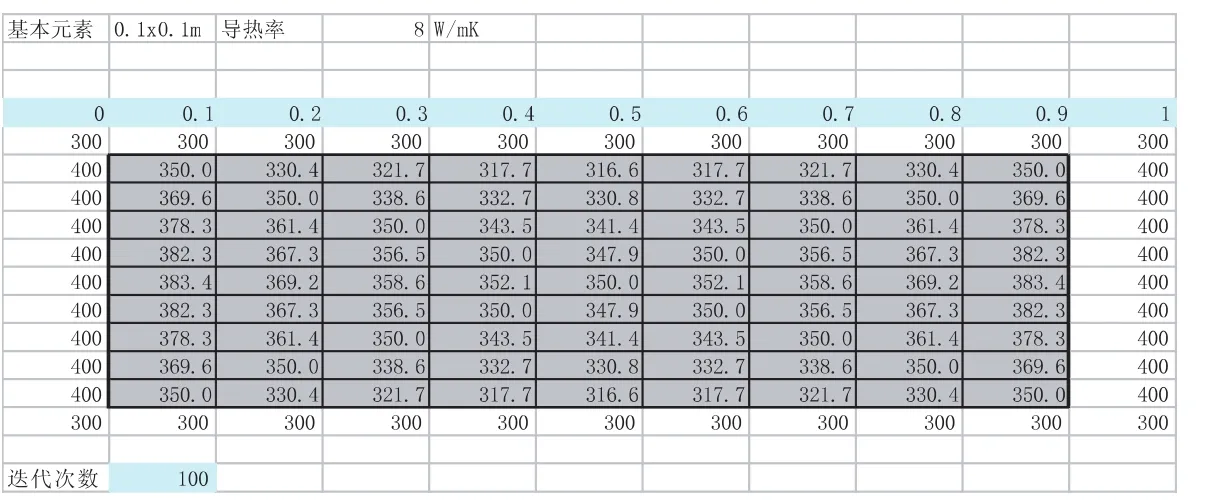
圖5 經過100次迭代后各單元格的溫度值

圖6 監控單元格溫度隨迭代次數的變化

圖7 金屬板穩定狀態時溫度分布云圖

圖6反映的是單元格B8，F12和J16溫度值隨著迭代次數的增加而不斷發展到傳熱穩定狀態，而圖7則是說明了在傳熱穩定狀態時金屬板的總體溫度分布。

3 電子表格在不同傳熱條件下的計算推廣

上面的內容一直是在闡述在無內熱源且定壁溫的計算。如果邊界條件發生變化，并且有內熱源的情況下，該如何去計算呢?

(1)在第二和第三類傳熱邊界條件下的差分方程。

圖8示意了第二和第三類的傳熱邊界條件。根據熱力學第一定律，式(5)可以得出:

對于式(5)，假設在深度方向上為單位長度。

圖8 邊界條件示意圖

如果熱流qb為常數，則式(5)屬于第二類邊界條件，所以該方程可以簡化為，

如果熱流qb不是常數，而是由對流換熱來決定的，則方程(5)屬于第三類邊界條件，所以該方程又可寫成:

(2)具有內熱源的第三類邊界條件下的差分方程。

基于圖8，如果點(m，n)上有一內熱源，則方程(5)須寫成:

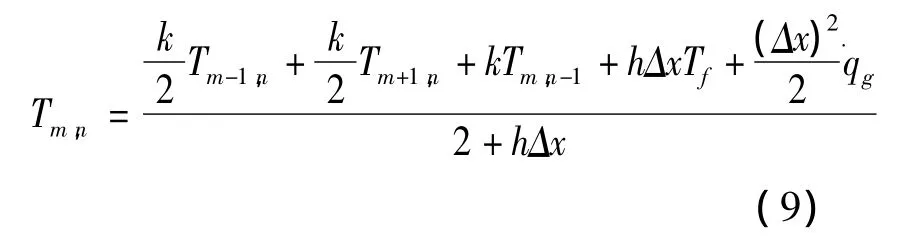
式(9)表示具有內熱源的第三類邊界條件下點(m，n)的差分方程。

根據以上方程(6)，(7)和(9)的結構形式，結合前面的計算示例，它們也是非常容易用電子表格的形式來表示。這樣常見的邊界條件及有內容情形下的傳熱問題都能夠用電子表格的方式去求解。因此，對于二維大多數的傳熱問題完全可以用電子表格法實現溫度分布。這種方法在研究電路板的熱分析，或單個散熱器的熱分析和優化，有著一定的現實意義。

此外，對于三維傳熱和瞬態傳熱問題，也是可以用電子表格去實現的。只不過差分方程變得稍微復雜而已，而且邊界條件的設置需要考慮清楚。

4 結語

通過上述的分析，可以看出電子表格確實能夠比較方便快捷地獲得散熱器的熱特性。而且，也可以將其延伸到多種邊界條件的傳熱問題中，甚至可以應用的電路板的熱設計中。當然，電子表格應用到數值分析中，需要有一些合理的假設，不能直接應用，否則會產生奇異的結果。通常應用在電子散熱中的散熱形狀比較簡單，這種電子表格法還是有一定的應用前景。

［1］ 楊世銘，陶文銓.傳熱學(第四版)［M］.北京:高等教育出版社，2010:105-107.

［2］ 賈力，方肇洪，錢興華.高等傳熱學(第二版)［M］.北京:高等教育出版社，2008.

［3］ 章熙民，任澤沛，梅飛鳴.傳熱學(第五版)［M］.北京:中國建筑工業出版社，2007.

［4］ KOHNO T，KOTAKEMORI H，NIKI H.Improving modified iterative methods for Z-matrices［J］.Liner Algebra and Its Application，1997，267:113-123.

［5］ 黃廷祝，楊傳勝.特殊矩陣分析及應用［M］.北京:科學出版社，2007:1-33.

［6］ 汪仲文.解線性方程組的迭代方法之比較［J］.喀什師范學院學報，2008(6):21-25.

［7］ LI Wen，SUN Weiwei.Modified Gauss-Seidel type methods and Jacobi type methods［J］.Linear Algebra and Its Application，2000，317:227-240.