基于Vague集記分函數的一種構造方法

王萬軍

(蘭州文理學院 信息工程學院 甘肅 蘭州 730000)

基于Vague集記分函數的一種構造方法

王萬軍

(蘭州文理學院 信息工程學院 甘肅 蘭州 730000)

在分析已有Vague集記分函數的基礎上，構造了一種新的Vague集記分函數，該記分函數能有效地刻畫不同風險偏好關系，克服了傳統(tǒng)記分函數的缺陷與不足.討論了新構造記分函數的涵義及構造準則.最后，通過實例分析比較了該記分函數的可行性和有效性.

Vague集； 記分函數； 構造方法

0 引言

自從Zadeh于1965年提出Fuzzy集[1]以來，Fuzzy集已被成功應用到社會諸多領域.Fuzzy集是通過定義在[0,1]上的一個單值隸屬函數來刻畫模糊問題，但實際上Fuzzy集無法表示支持(肯定)、反對(否定)和猶豫(不確定)的證據.Gau和Buehrer于1993年推廣了Fuzzy集，提出了同時能考慮隸屬與非隸屬2個方面信息的Vague集[2].Vague集定義了一個[0,1]區(qū)間上真隸屬函數tA(x)和假隸屬函數fA(x)來刻畫信息的模糊性,Vague集克服了Fuzzy集的不足與缺陷，在信息處理、工業(yè)控制、決策分析及模式識別等領域得到廣泛應用.但作為Vague集關鍵問題之一的記分函數研究，目前雖然一些學者進行了相關研究[3-11],但仍然存在許多問題.

本文針對目前Vague集記分函數相關文獻及資料，結合不同決策者風險偏好情況，構造了一種帶偏好風險決策的Vague集記分函數.通過實例比較分析，發(fā)現該方法是一種可行有效的記分函數.

1 已有Vague集記分函數不足及分析

已有文獻中具有代表性Vague集記分函數，主要有如下幾種：

(1)Chen與Tan的記分函數[3]

Chen與Tan于1994年首次提出了Vague集的記分函數SC(x)=tx-fx.SC(x)只考慮了支持證據tx與反對證據fx，該記分函數容易造成信息丟失，甚至結果的錯誤.

為了彌補Chen等人方法的不足，文獻[4]提出用精度函數H(x)=tx+fx來判斷SC(x)相同時決策信息優(yōu)劣.

(2)李凡等人的記分函數[5]

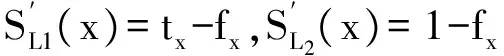
李凡等人的記分函數只考慮了2種極端(悲觀決策與樂觀決策)，沒有考慮中立狀態(tài)，有不足之處.

(3)劉華文的記分函數[6]

該記分函數將未知度πx進行二次分配,給支持度tx，反對度fx與猶豫度(1-tx-fx)πx3部分進行構造新的記分函數,即SL(x)=tx+(1-tx-fx)tx.SL(x)記分函數的最大不足是：對任意Vague值tx=0，則恒有SL(x)=0，顯然這是不合理的.

(4)周珍等人的記分函數[7]

該記分函數為SZ(x)=tx-fx+(α-β)πx,其中參數α,β∈[0,1]，α+β∈[0,1].該記分函數的缺點是參數α,β的選擇比較難掌握，由于α,β選擇不當導致結果不合理.

(5)Ye J的記分函數[9]

Ye J將記分函數定義為SY(x)=tx-fx+μπx，其中參數μ∈[-1,1].該記分函數缺點與SZ(x)記分函數一樣，參數μ選擇不恰當會導致結果的不合理或不正確.

(6)王偉平的記分函數[10]

該記分函數定義為

SME(x)記分函數根據決策者中立、厭惡與追求心態(tài)構造了一種分段的記分函數，雖然該方法能較好地反映決策者偏好心態(tài)，但該記分函數在信息決策時容易造成信息偏好極端化，即當支持證據占優(yōu)勢時，采用追求心態(tài)決策時未確知信息πx全部激進支持證據；當反對證據占優(yōu)勢時，采用厭惡心態(tài)決策時，未確知信息πx全部追隨反對證據.從理論上來說是不合理的.

2 Vague集及記分函數

2.1 Vague集

定義1[2]設U是一個論域,?x∈U，對U上的一個Vague集描述用一個真隸屬函數tA(x)和一個假隸屬函數fA(x)來表示.即tA(x):U→[0,1],fA(x):U→[0,1],其中tA(x)+fA(x)∈[0,1].

tA(x)描述了支持證據的隸屬度下界，fA(x)描述了反對證據的隸屬度下界.

定義2 稱[tA(x),fA(x)]是x在Vague集A上的Vague值，πA(x)=1-fA(x)-tA(x)是x在Vague集A上的未知度或猶豫度.

πA(x)反映了x相對A的未知信息量，πA(x)越大，未知信息量越多，當πA(x)=0時，Vague集退化為Fuzzy集.相反1-πA(x)反映了x相對A的確知信息量，1-πA(x)值越大，確知信息量就越多.

2.2 Vague集記分函數

Vague集中記分函數S(x)是用來衡量決策方案對于決策屬性要求滿足程度的一種衡量標準，是由Chen等人[3]于1994年在討論Vague集的多準則模糊決策問題時首次提出的.記分函數是Vague集多屬性決策的關鍵和核心，它是Vague集中進行模糊不確定信息集結處理的直接集中與體現.因此,Vague集中記分函數構造的優(yōu)劣直接影響了Vague集決策的優(yōu)劣，甚至影響決策結果的正確與否.

3 本文的構造方法

3.1 記分函數涵義分析

為有效構造記分函數，應該將Vague值x=[tx,fx]中tx，fx與πx所包含的信息全面考察分析.其實在Vague值中，確定的信息有2部分：一部分為tx-fx，給出了支持證據與反對證據的偏勢?Δ(優(yōu)勢)[12]，?Δ值越大，S(x)越大；反之，?Δ值越小，S(x)越小.另一部分為猶豫度πx以外的1-πx，給出了未確知度以外的已確知信息，1-πx越大，已確知信息越多；反之，1-πx越小，已確知信息越少.

在Vague記分函數構造中應包含這2部分信息，但決策者在記分函數構造中經常會出現悲觀、中立或樂觀等偏好心態(tài)，因此在記分函數S(x)構造中還要考慮決策者決策偏好情況及πx在決策偏好時趨向于偏好的程度.為了能夠構造有效、合理、準確的Vague記分函數S(x)，則S(x)應該滿足如下的準則：

準則1：(tx-fx)≥(ty-fy)，則S(x)≥S(y)；反之亦然.

準則2：樂觀決策中，當tx?fx時，有ΔS(x)?ΔS(y).

準則3：悲觀決策中，當txfx時，有ΔS(x)ΔS(y).

準則4：中立決策中，有ΔS(x)≈ΔS(y).

3.2 本文記分函數

在分析前述Vague記分函數基礎上，本文構造了如下記分函數.為表達方便，先定義幾個概念.

定義4 對Vague值x=[tx,fx]，稱H(x)=1-πx為Vague值x的精確度或已確知度.

定義5 對Vague值x=[tx,fx]，稱?Δ(x)=tx-fx為Vague值x的偏勢或優(yōu)勢.

其實H(x)和?Δ(x)在Vague集中類似于統(tǒng)計學中的方差和均值概念[13].?Δ(x)越大，且H(x)越小，則構造記分函數結果越優(yōu).

定義6 對Vague值x=[tx,fx]，定義記分函數為

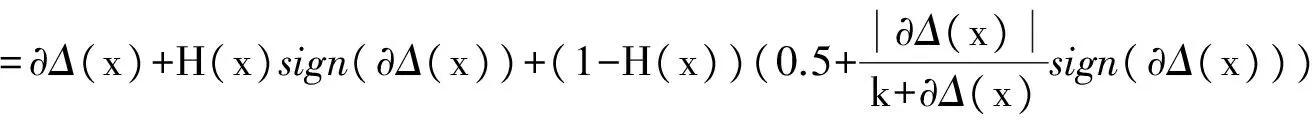
其中k是一個校正參數(k≥1)，起到對記分函數結果誤差校正作用.在實際計算中，為了計算方便，通常取k=1.

對定義6，其實由3部分組成：

第1部分：?Δ(x)為偏勢部分，與決策偏好無關.

第2部分：H(x)為精確度或已確知度部分.這部分與決策偏好相關，通過函數sign(x)進行不同決策偏好趨向處理.

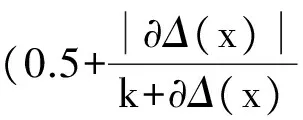
顯然定義6記分函數包含了Vague值中tx，fx與πx全部信息在不同決策心態(tài)下偏好趨向的總值，同時該記分函數體現決策時少數服從多數的原則和心理學決策中“馬太效應”[10].因此定義6記分函數具有適用性和可行性.

從定義6 易知，該記分函數SW(x)滿足準則1到準則4的要求.

4 結果比較分析

為便于比較本文構造的記分函數有效性、合理性和可行性，采用文獻[10]為例進行分析，結果見表1所示.

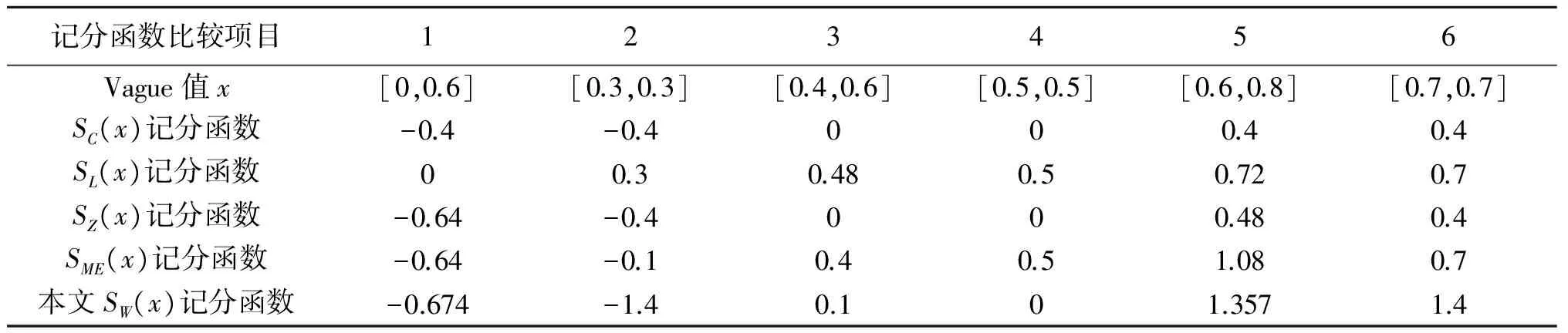
表1 本文記分函數與已有相關文獻結果比較Tab.1 The comparison results of this paper score function with the existing literatures

從表1可知：

SC(x)記分函數與SZ(x)記分函數沒有分辨率，不能區(qū)分[0.4,0.6]，[0.5,0.5]，而SL(x)與SME(x)記分函數雖然能分辨，但其缺點前面已經分析，并且SME(x)記分函數中[0.6,0.8]優(yōu)于[0.7,0.7]的結論明顯有誤.本文SW(x)記分函數具有較好的分辨率，它能反映出實際客觀和直覺模糊的要求，符合人類思維認知規(guī)律.因此SW(x)記分函數是可行的、有效的，并有較好分辨率.

5 結論

本文在分析已有Vague集記分函數的同時，指出了現有記分函數的不足與缺陷，討論并構造了Vague集記分函數相關準則及涵義，在此基礎上，給出了一種新的Vague集記分函數.最后通過實例比較分析了該方法的可行性和有效性.

[1] Zadeh L A. Fuzzy sets[J].Information and Control,1965,8(3):338-357.

[2] Gau W L,Buehrer D J. Vague sets[J].IEEE Transactions on Systems, Man and Cybernetics, 1993,23(2):610-614.

[3] Chen S M, Tan J M. Handling multi-criteria fuzzy decision-making problems based on Vague set theory[J]. Fuzzy Sets and Systems, 1994,67(2):163-172.

[4] Hong D H, Choi C H. Multi-criteria fuzzy decision-making problems based on Vague set theory[J]. Fuzzy Sets and Systems, 2000,114(1):103-113.

[5] 李凡,盧安,蔡立晶.基于Vague集的多目標模糊決策方法[J].華中科技大學學報:自然科學版,2001,29(7):1-3.

[6] 劉華文.多目標模糊決策的Vague集方法[J].系統(tǒng)工程理論與實踐,2004,24(5):103-109.

[7] 周珍,吳祈宗,蘭曉亭.基于記分函數的區(qū)間值Vague集的相似度量[J].小型微型計算機系統(tǒng),2006,27(6):1001-1012.

[8] 王愛領.基于改進的Vague-Topsis方法的公租房輪候排序評價研究[J].鄭州大學學報：理學版，2013，45(3):115-119.

[9] Ye J. Improved method of multi-criteria fuzzy decision-making based on Vague sets[J]. Fuzzy Sets and Systems, 2007,39(2):164-169.

[10]王偉平.基于Vague集的語言型多準則決策方法[M].北京：經濟科學出版社，2013:66-68．

[11]虎曉紅,錢旭,蘭洋.基于Vague融合的自動圖像標注方法[J].鄭州大學學報:理學版，2010，42(1):41-44.

[12]王萬軍,李恒杰,胡建軍,等.基于Vague值轉化Fuzzy值的一種新方法[J].計算機工程與應用,2012,48(36):134-136.

[13]徐澤水.直覺模糊信息集成理論及應用[M].北京：科學出版社，2008:2-5．

A Construction Method Based on Score Function for Vague Sets

WANG Wan-jun

(InformationEngineeringCollege,LanzhouUniversityofArtsandScience,Lanzhou730000,China)

Based on present score function for Vague sets, a new score function was constructed for Vague sets. The method could effectively describe the different risk preference relation, and overcome the defects and shortcomings of the traditional score function. The meaning and criterion of the new structure score function were discussed. Finally, an example was given to analyze the feasibility and effectiveness of the method.

Vague sets; score function; construction method

2013-08-27

甘肅省高等學校研究生導師科研項目，編號1215-04；甘肅省教育廳科研項目，編號1113-01；蘭州文理學院科研能力提升計劃骨干項目，編號2012GGTS01.

王萬軍(1974-)，男，副教授，主要從事計算機智能信息處理與信息決策分析技術研究，E-mail: wangwanjun1@163.com.

TP 301

A

1671-6841(2014)01-0033-04

10.3969/j.issn/1671-6841.2014.01.008