靜電陀螺監控器六次校準與赤道陀螺方位環隨動性能關系分析

周海淵，潘 良，倪文秀，陳 思

（1.中國衛星海上測控部，江陰 214431；2.天津航海儀器研究所，天津 300131）

靜電陀螺監控器六次校準與赤道陀螺方位環隨動性能關系分析

周海淵1，潘 良1，倪文秀2，陳 思1

（1.中國衛星海上測控部，江陰 214431；2.天津航海儀器研究所，天津 300131）

靜電陀螺監控器可以全天候提供連續高精度的位置及航向信息，且不受天氣制約。但是在低緯度海域靜電陀螺監控器會出現六次校準頻繁重置的現象，導致靜電陀螺無法獲得準確的漂移模型系數，進而影響到設備的正常工作。針對上述現象，通過分析設備結構和工作原理，構建了赤道陀螺隨動性能數學模型，推導出赤道陀螺方位環隨動速率與所在緯度相關性的計算方法，研究了六次校準重置與赤道陀螺隨動性能的關系，提出了低緯度地區六次校準重置現象的規避方法。研究結果有效拓展了靜電陀螺監控器的啟動緯度范圍，提高了設備應用效益。

靜電陀螺監控器；六次校準；隨動性能；赤道陀螺

航向信息是影響測量船測控定軌精度的關鍵因素之一[1]。與傳統的基準航向測量設備光學經緯儀相比，靜電陀螺監控器具有不受天氣制約且能夠提供實時航向信息的優勢。

然而在實際應用中，該設備在低緯度地區經常出現六次校準無法正常通過的現象[2]，導致設備無法正常工作。

1 六次校準重置與赤道陀螺方位隨動性能關系

EGSM工作流程需要經歷陀螺啟動、六次校準、48 h標定、導航四個階段。其中，六次校準階段測量陀螺的初始赤緯及時角，為保證六次校準測量的精確性，系統設置了以下約束條件：∣ah2∣＞87o，即赤道陀螺（下陀螺）高度角原始測量值與高度角角度傳感器零位的差值大于87o時六次校準重置。

1.1 赤道陀螺方位角隨動速率計算方法

在靜電陀螺監控器系統中，將極軸陀螺和赤道陀螺的主軸指向代表的兩個虛擬“星體”分別以B1和B2表示，在理想情況下，極軸陀螺動量矩軸與天北極Pn重合，赤道陀螺動量矩軸位于赤道平面內[3-6]，使“星體”B2的赤緯δ2＝0。赤道陀螺對應的天文三角形如圖1所示。

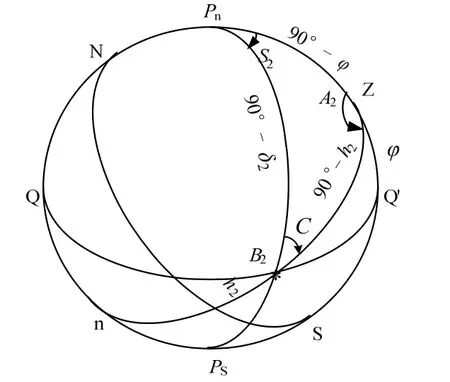
圖1 赤道陀螺星體對應的天文三角形Fig.1 Astronomy triangle relation of equator-gyro

圖1中，由天頂Z、天北極Pn和陀螺星體B2構成球面三角形，三個角分別為方位角A2、地方時S2和C角；對應的三個邊分別為 90o-δ2、90o-h2和 90o-φ。這里δ2≈0，h2為赤道陀螺高度角，φ為緯度。

根據球面三角形的變換公式，可以得到：

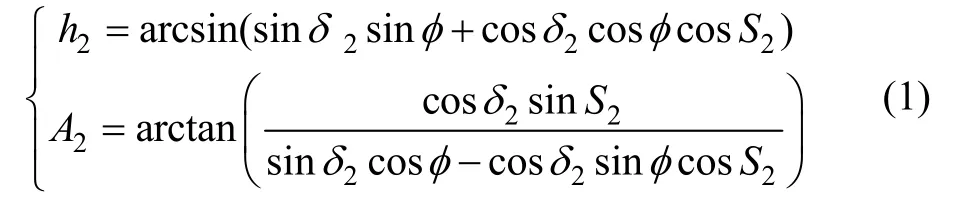
式(1)即為赤道陀螺的高度角和方位角公式。式(1)對時間求導數即可得到h2和A2的變化率，下面給出h2和A2變化率的簡化公式及推導過程。

根據圖1中的球面三角形可以得到：

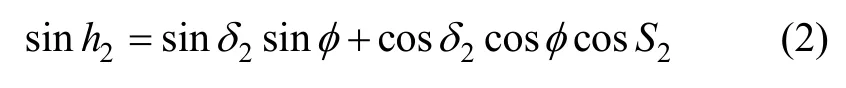
在靜電陀螺監控器中，陀螺星體的赤緯δ啟動后基本為常值，對于在艦船導航系統中緯度φ變化相對地球自轉也是小量，可認為是常量，因此，式(2)兩邊對時間求導可得：

根據球面三角形的關系有：

將式(1)代入式(3)中，可得：

由于S2=Sg0+Ωt+λ，其中Sg0為赤道陀螺的初始格林時角，Ω為地球自轉角速度，λ為經度，可得dS2/dt=Ω，代入式(5)即可得到h2變化率的簡化公式：

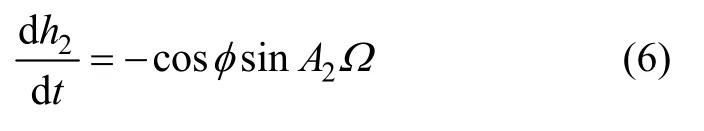
根據式(4)可得：

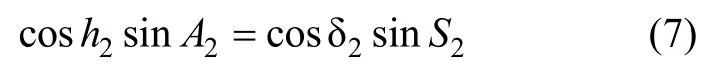
式(4)兩過對時間求導，并認為δ2為常值，得：

根據球面三角形關系，有：

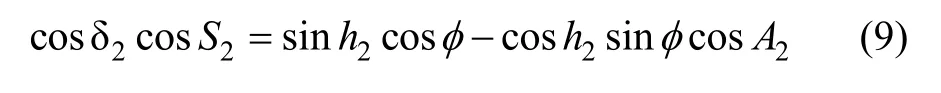
將式(9)(5)代入式(8)，整理得：

根據球面三角形關系，有：

將式(1)代入式(10)，整理得：

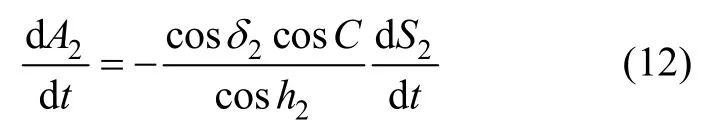
根據球面三角形關系，有：

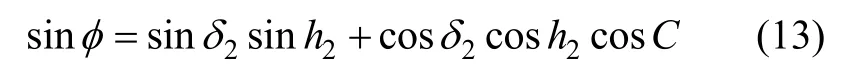
將式(13)代入(12)，做 sinδ2≈0 近似，可獲得A2變化率的簡化公式：

靜電陀螺監控器赤道陀螺高度角h2變化范圍為：0o～90o-φ，當h2=90o-φ時，A2最大變化率為：

1.2 赤道陀螺方位角隨動性能與六次校準關系研究

在緯度為±5°范圍內，根據式(15)計算出緯度與赤道陀螺方位角變化率之間的關系，結果如圖2所示。在計算中地球自轉角速度取值Ω=15 (o)/h。

從圖2的緯度與赤道陀螺方位角變化率關系不難驗證，在赤道附近赤道陀螺方位環理論上需要極高的隨動性能才能滿足設備工作需求[7]。在南北緯3o和2o，理論上赤道陀螺方位角最大變化率絕對值分別為0.0796 (o)/s和 0.1196 (o)/s，即赤道陀螺方位隨動達到上述性能才能保證在相應海域內正常工作。

依據六次校準約束條件，赤道陀螺高度角h2絕對值不能大于87o，即在緯度±3°內設備理論無法工作。然而根據設備實際工作情況統計，ESGM在該緯度區域內并不是每次都出現六次校準無法通過的現象，某一特定ESGM設備六次校準重置的極限條件根據設備具體情況有所區別。對某一ESGM設備近30次啟動工作情況進行統計，設備六次校準通過最低緯度記錄為北緯2o，對應赤道陀螺高度角與赤道陀螺方位角變化率情況如圖3所示。

圖3數據分析表明此ESGM設備工作過程中赤道陀螺高度角最大為87.71o，對應最大方位角變化率為0.1041 (o)/s。上述數據可以視為該ESGM設備六次校準重置的極限條件。如果該設備啟動要避免六次校準重置現象發生，必須規避上述極限條件發生。

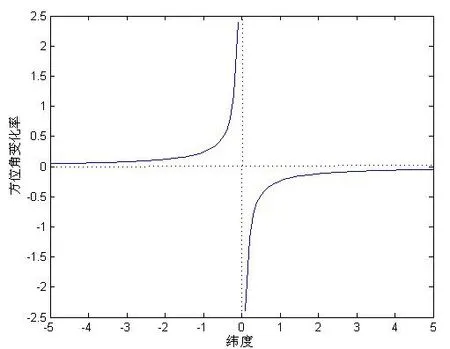
圖2 緯度與赤道陀螺方位角變化率關系Fig.2 Relation between latitude and azimuth angle change velocity of equator-gyro

圖3 某次試驗赤道陀螺高度角與赤道陀螺方位變化率Fig.3 Relation between height angle and azimuth change velocity of equator-gyro

2 六次校準重置規避方法

從前面分析可以得出規避低緯度地區ESGM六次校準重置現象有兩種方法，一是提高赤道陀螺方位環隨動性能，二是在設備工作過程中盡可能減小設備啟動過程引入的誤差，同時有效規避赤道陀螺高度角和方位角變化率超出設備隨動性能。

相關措施主要包括以下方面：

1）ESGM 設備啟動前支撐慣導必須經過充分校準，航向、位置、水平姿態精度必須滿足指標要求，減小慣導引入誤差對六次校準造成影響。

2）設備啟動需要6 h以上等緯度航行工況保障，極軸陀螺和赤道陀螺分時啟動，阻尼定中時間要大于40 min，以減小設備啟動中陀螺動量矩軸定向誤差對六次校準的影響。

3）由于不同陀螺的隨動性能不同，根據積累的試驗數據，計算每個陀螺的方位隨動性能，盡量避免在滿足陀螺隨動性能的范圍內啟動設備或者進行六次校準。

4）赤道陀螺高度角和方位角變化率的極大值每六小時出現一次，如果在低緯度啟動設備，六次校準過程中船舶應該向高緯度區域機動，減小赤道陀螺方位角隨動負擔，以免出現六次校準重置甚至是陀螺“未捕獲”告警。

上述方法在設備啟動中進行了多次應用，有效規避了六次校準重置的現象。

3 結 論

靜電陀螺監控器在低緯度海域對赤道陀螺方位環的隨動性能要求極高，設備容易出現六次校準重置現象。本文從分析設備工作原理入手，構建了赤道陀螺隨動性能數學模型，推導出了赤道陀螺方位環隨動速率與所在緯度相關性的計算方法，研究了六次校準重置與赤道陀螺隨動性能的關系，從理論和實際應用兩個方面提出了規避低緯度地區六次校準重置的辦法。

本文的研究成果拓展了靜電陀螺監控器的啟動緯度范圍和設備的應用效益。

（References）：

[1]馮鴻奎，李曉勇，薛國虎，等.航天測量船導航系統ESGM技術[J].飛行器測控學報，2010，29 (1)：28-33.FENG Hong-kui,LI Xiao-yong,XUE Guo-hu.et al.Application of ESGM technique on space instrumentation ships[J].Journal of Spacecraft TT &C Technology,2010,29 (1):28-33.

[2] 劉新民，孫學成，周琳琦，等.靜電陀螺監控器海上“六次校”方法[J].中國慣性技術學報，2011，19(4)：309-402.LIU Xin-ming,SUN Xue-cheng,ZHOU Lin-qi,et al.Method of electrostatic gyroscope monitor’s maritime six-times calibration[J].Journal of Chinese Inertial Technology,2011,19(4):309-402.

[3]Christensen W.Advanced development of ESG strap down navigation system[J].IEEE Transactions on Aerospace and Electronic Systems,1996,2(2) :143-157.

[4]ZHANG Ke-zhi,TIAN Wei-feng,QIAN Feng.Combination of distributed Kalman filter and BP neural network for ESG bias model identification[J].Transactions of Nanjing University of Aeronautics &Astronautics,2010,27(3):226-231.

[5]Yang Gong-liu.Study on simulation techniques for marine integrated navigation system[C]//Second International Symposium on Inertial Technology in Beijing.Beijing,October 1998.

[6]Hill D A,Letendre T,Mills H A.Embedded real-time DSP control of an electrostatically gyroscope[C]// Proceeding of the American Control Conference.Boston 2004.

[7]王前學，倪文秀，劉巍，等.靜電陀螺監控器海上赤道陀螺儀低緯度下的隨動性能[J].中國慣性技術學報，2010，18(1)：90-92.WANG Qian-xue,NI Wen-xiu,LIU Wei,et al.Servo performance of ESGM’s equatorial gyroscope in low-latitude regions[J].Journal of Chinese Inertial Technology,2010,18(1):90-92.

Relation analysis between six-calibration and follow capability of equator-gyro about ESGM

ZHOU Hai-yuan1，PAN Liang1，NI Wen-xiu2，CHEN Si1
(1.China Satellite Maritime Tracking &Controlling Department，Jiangyin 214431，China;2.Tianjin Navigation Instrument Research Institute，Tianjin 300131，China)

Compared with traditional optical theodolite，a high-precision course information can be supplied by ESGM at all-weather.While in low latitude areas，the Six-Calibration of ESGM may be frequently reset by the poor follow capability of equator-gyro，and the accurate ESG drift model coefficient is unable to be obtained.In this paper，according to the former phenomenon，the follow capability of equator-gyro about ESGM is calculated in principle，and the relation between six-calibration and capability of equator-gyro is analyzed.An effective method is put forward to avoid six-calibration to be reset in low latitude areas.The research results show that the ESGM start latitude range can be effectively expanded，and the application efficiency can be improved by the proposed method.

ESGM;six-calibration;follow capability;equator-gyro

U666.1

A

1005-6734(2014)03-0281-03

10.13695/j.cnki.12-1222/o3.2014.03.001

2014-01-24；

2014-04-29

周海淵（1982—），男，工程師，從事慣性導航設備應用研究。E-mail：lynn9527@gmail.com