基于仿射修正技術的水下地形ICCP匹配算法

徐曉蘇，吳劍飛，徐勝保，王立輝，李佩娟

（1.微慣性儀表與先進導航技術教育部重點實驗室，南京 210096；2.東南大學 儀器科學與工程學院，南京 210096）

基于仿射修正技術的水下地形ICCP匹配算法

徐曉蘇，吳劍飛，徐勝保，王立輝，李佩娟

（1.微慣性儀表與先進導航技術教育部重點實驗室，南京 210096；2.東南大學 儀器科學與工程學院，南京 210096）

ICCP匹配算法是水下組合導航系統中最為重要的匹配算法。針對傳統ICCP匹配算法存在僅對水下航行器慣性導航系統指示航跡作旋轉和平移的剛性變換的局限性問題，為提高水下航行器地形輔助導航系統中匹配算法的精度，分析了水下航行器慣性導航系統誤差特性，建立了誤差模型，提出了基于仿射修正技術的水下地形ICCP匹配算法。首先利用ICCP匹配算法對慣性導航系統指示航跡進行剛性變換，再利用最小二乘法求解仿射參數，進而對ICCP匹配航跡進行仿射修正。仿真研究表明，基于仿射修正技術的ICCP匹配算法能較好地解決傳統ICCP匹配算法剛性變換的局限性，匹配精度優于傳統ICCP算法，匹配誤差小于數字地圖網格間距的50%，同時仿射修正所耗費時間極少，所增加的時間僅為傳統ICCP匹配算法匹配時間的千分之一。

水下航行器；慣性導航；地形匹配；ICCP；仿射變換

水下航行器因其在未來的軍用和民用領域都具有重要的戰略意義而成為了世界上軍事強國重點發展的領域。水下航行器有高度隱蔽性和保持長時間精確航行的要求，而實現這一要求的關鍵技術之一是其導航技術。水下的導航方式有別于陸路導航，GPS、無線電等導航方式因水中信號迅速衰減而不適用于水下航行器。慣性導航因其具有自主性、隱蔽性等優點，成為了水下航行器導航手段的首選。但慣性導航有固有的缺陷，其誤差會隨著時間的積累逐漸增大，因而在慣性導航定位系統運行一段時間后必須采用外來信息對慣性導航系統進行修正。隨著導航技術特別是組合導航技術的發展，應用地形、重力、地磁等信息來輔助慣性導航[1]為水下航行器導航研究提供了一種新思路。由于地形高程信息測量較為方便，且陸路上的地形匹配技術已應用于實際，可為水下地形匹配導航提供借鑒，因而應用地形高程信息來輔助水下航行器的導航具備高度可行性。

ICCP（Iterative Closest Contour Point）算法是目前水下地形匹配導航技術最為重要的匹配算法之一，其本質為相關極值匹配算法[2]。但是ICCP算法對慣導航跡所作的修正僅僅是旋轉和平移，沒有對航跡進行縮放，因而不能修正輔助定位過程中慣導指示航跡相對于實際航跡發生的形變所造成的誤差，因此本文引入了仿射修正技術，以解決 ICCP算法的缺陷，提高匹配精度。

1 ICCP算法

ICCP算法最初由圖像配準算法 ICP（Iterative Closest Point）發展而來的[2]。國內外許多專家、學者對ICCP算法進行了系統研究，Behzad K.P.首次將該算法引入重力匹配輔助導航，并對其實現形式進行了較為詳細的闡述。Bishop通過大量仿真試驗系統地分析了該算法的可行性及誤差影響[3]，劉承香詳細分析了 ICCP算法在地形匹配輔助導航的適用性，并對ICCP關鍵技術展開了研究[4]。

1.1 ICCP算法描述

ICCP算法匹配[4-7]示意圖如圖1所示。水下航行器沿著實際航跡序列(N為采樣點個數)航行過程中，由于慣性導航系統存在誤差，因此主慣導系統會給出一個偏離實際航跡序列的指示航跡序列，與此同時，測深裝置也記錄測得的水深序列。在測深裝置沒有誤差的情況下，可以確定實際航跡序列一定位于根據實測水深信息序列生成的水深等值線上。通常認為，主慣導系統給出的位置信息在一定誤差范圍內是可信的，因此可以將主慣導系統的指示航跡序列作為待匹配航跡序列，根據水深信息序列在數字地圖中生成等值線并在等值線上的提取最近點序列作為匹配目標，迭代地尋找剛性變換T，T包括一個旋轉量R和一個平移量t，使以下目標函數最小：

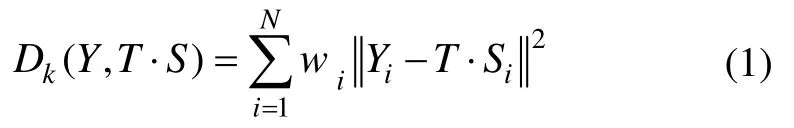
其中，wi代表其中各序列點的權值，k代表第k次迭代過程，N代表航跡序列點個數。

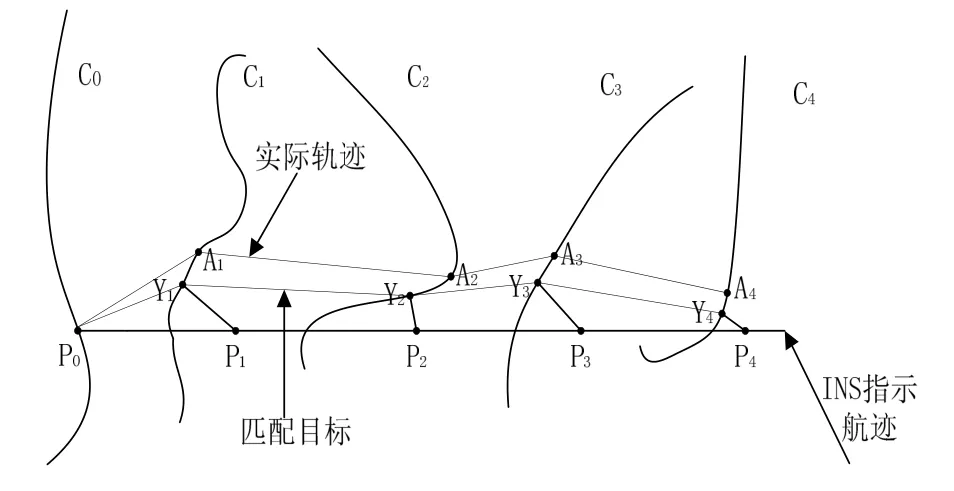
圖1 ICCP算法匹配示意圖Fig.1 Description of ICCP algorithm

利用四元數法[4]找到剛性變換T后，對待匹配航跡序列作剛性變換T·Si：

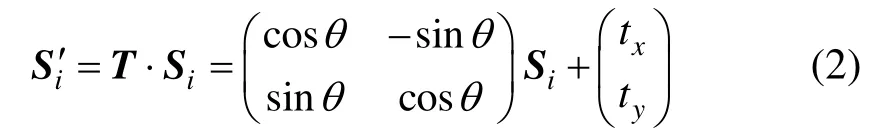
1.2 ICCP算法的缺陷

主慣導系統的定位誤差有如下特性：

根據加速度計的偏移、陀螺儀的漂移以及慣性導航系統的輔助定位周期可以得出[8]：

●水下航行器運行一段時間后，主慣導定位系統給出的位置存在一定的誤差，計為，其中Xδ為緯度誤差，Yδ為經度誤差。

●通常地形輔助定位的時間比較短，因而可得出該段時間內，慣導解算的速度v為：其中，vr為水下航行器的真實速度，vδ為輔助定位前航行器速度積累誤差，vε為輔助定位過程中速度誤差的變化量。速度誤差主要是由加速度計零偏和重力加速度在水平姿態誤差上的投影所造成，由于地形輔助定位時間內引起的速度誤差遠小于航行器輔助定位之前引起的誤差，故式(3)可以簡化為：

●同理于速度解算的分析，可得慣導解算的航向d：

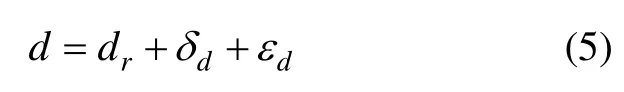
其中，dr為水下航行器的真實航向，dδ為航行器在輔助定位前航向積累誤差，dε為輔助定位過程中因誤差引起的航向變化量。同理于速度解算，計算航向的式(5)也可以簡化成：

由前面的分析可得，在慣導修正的這段時間，慣導解算航跡和航行器實際航跡之間的關系為：

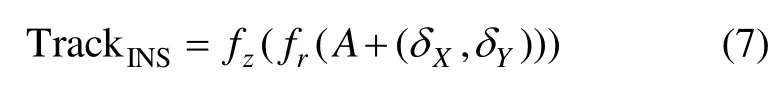
通過上述對主慣導系統誤差特性分析可得，由于加速度計的偏移、陀螺儀的漂移，主慣導系統的指示航跡和水下航行器實際航跡之間的關系不僅存在旋轉和平移，而且也存在縮放，因而不是一種僅包旋轉和平移的剛性變換關系。ICCP算法作了實際航跡是水下航行器慣性導航系統的測量航跡的平移和旋轉的剛性變換的假設，因而匹配的誤差較大。

針對這一缺陷，可引入仿射模型[8]來對ICCP匹配后的航跡進行再次修正，以提高匹配精度。通過模擬退火等算法來搜索仿射變換因子的最優解以實現航跡匹配的計算量較大，難以滿足水下航行器地形匹配的實時性要求，因此本文綜合考慮了匹配精度和效率，采用最小二乘法來求解仿射參數，提高算法實時性，再對 ICCP匹配算法的匹配結果進行仿射變換，以解決ICCP匹配算法所存在的缺陷，提高匹配精度。

2 仿射變換算法

2.1 仿射變換數學描述

通過對慣導系統的誤差模型的分析，可以建立一個簡單仿射變化模型[9-10]，包含平移、旋轉、縮放三種變換，分別對應于水下航行器的初始位置誤差、航向角誤差、速率誤差。其數學描述可表示為：

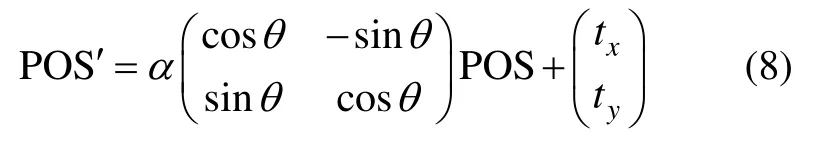
其中，POS為變換前的位置信息，POS’為變換后的位置信息，θ為旋轉角，對應于航向角誤差；α為縮放量，對應于速率誤差；tx、ty為平移量，對應于初始位置誤差。

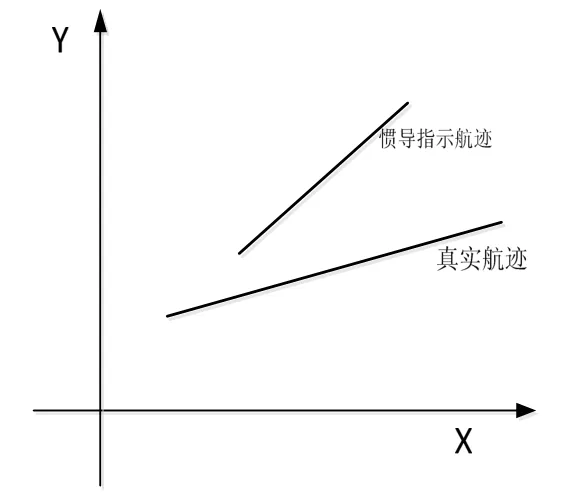
圖2 仿射模型示意圖Fig.2 Description of affine model

2.2 仿射變換參數求解

仿射變換參數求解具體方法敘述如下：

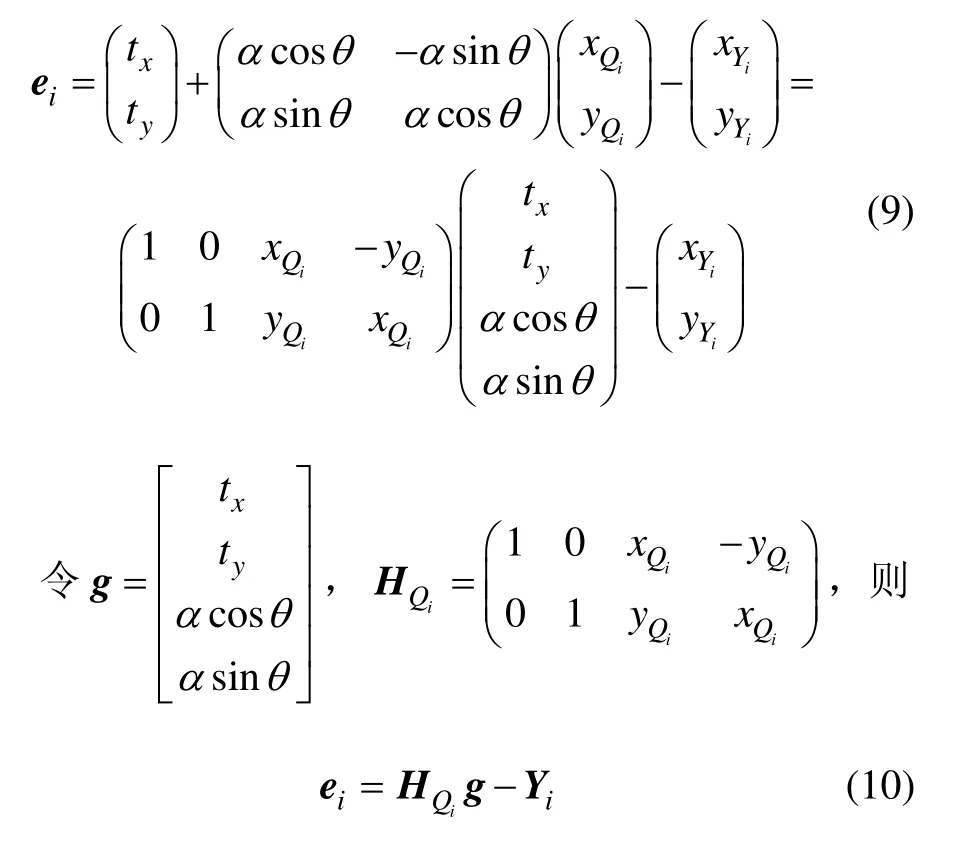
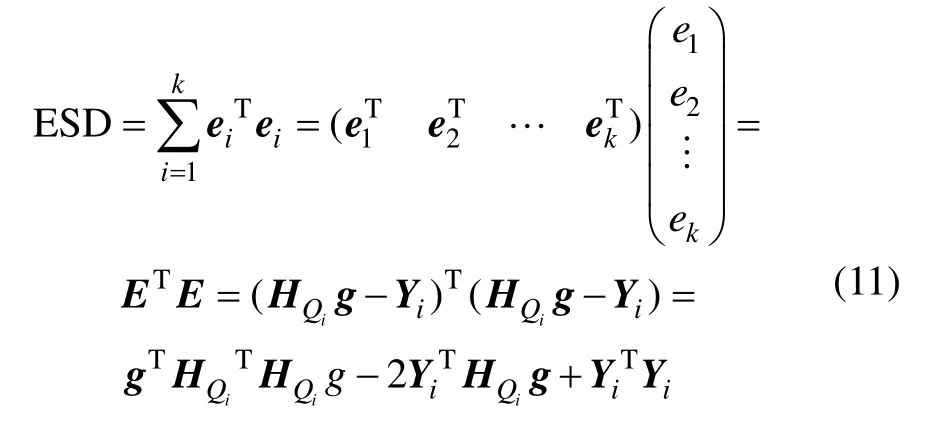
將求得ESD(tx,ty,α,θ)最小時候的g記為，對ESD求導可得：

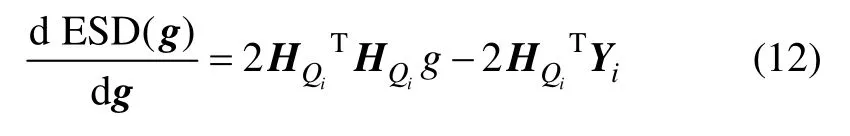
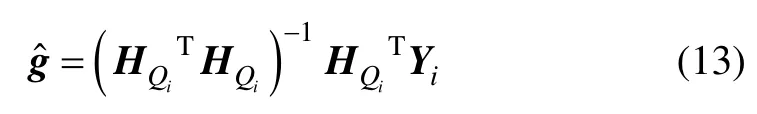
由于ESD對g的二階導數

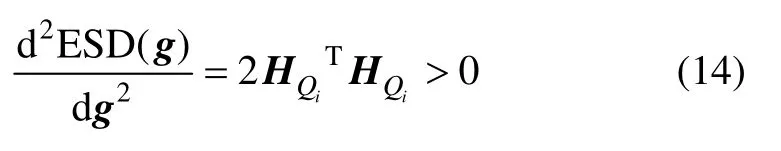
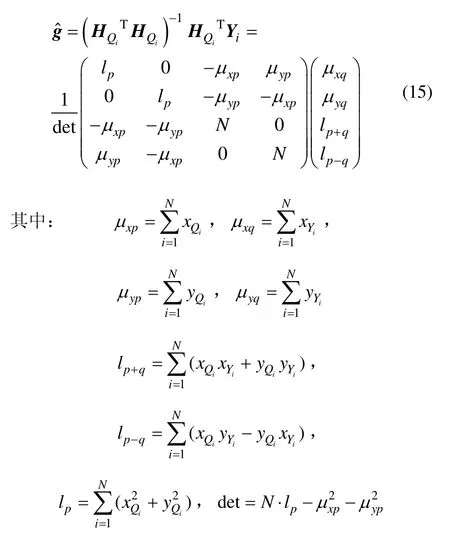
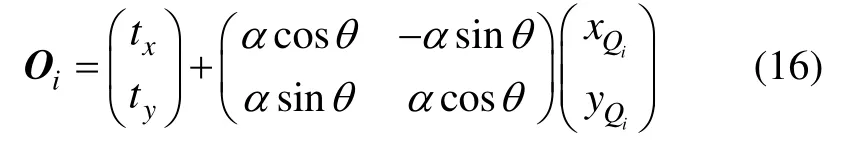
3 仿射修正ICCP匹配算法

基于仿射修正的ICCP匹配算法具體敘述如下：

第一步：在匹配區建立的規則網格數字地圖上提取等深線。

第二步：由主慣性導航系統的位置信息序列和航行過程中實際測量的水深信息，得到一個預匹配的初始對準航跡。

第三步：應用ICCP算法，對初始對準航跡進行剛性變換，尋找全局最優的航跡。

第四步：應用仿射變換，對由ICCP算法得到的最優航跡進行縮放和旋轉變換。

第五步：對最后得到的航跡進行精度評估，利用成功匹配的結果修正主慣導系統。

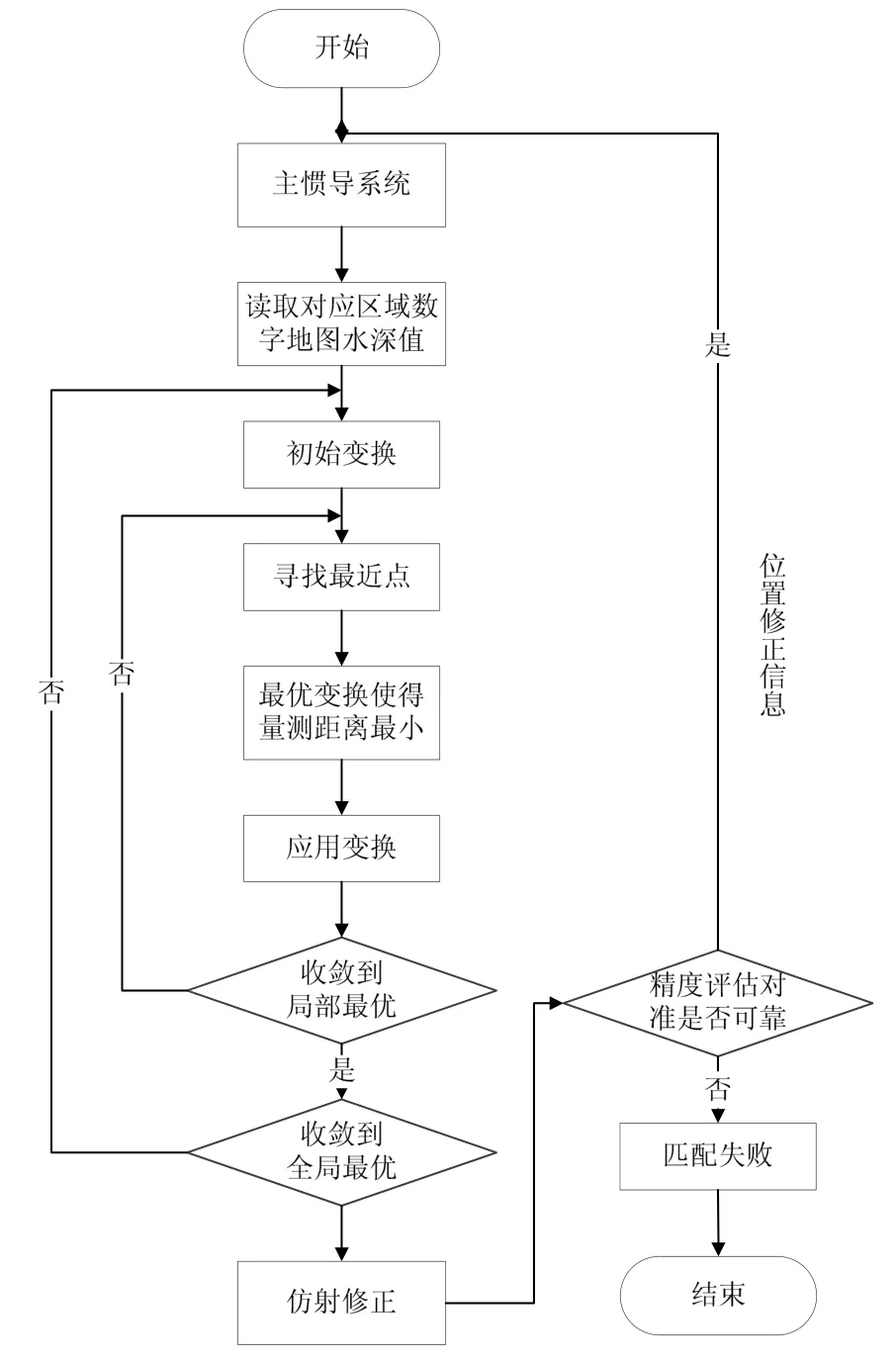
圖3 射修正ICCP算法流程圖Fig.3 Flow chart of ICCP algorithm based on affine correction

4 仿真實驗

為了驗證本文所述匹配方法在不同特征地形[11]上的有效性，本文在選取了兩塊特征不同的地形，其中地形a水深標準差為5.7029，地形b水深標準差為7.8779，如圖4(a)、圖4(b)所示。在每塊地形上規劃三條不同的航跡，再利用 ICCP算法和仿射修正 ICCP算法進行匹配，比較匹配誤差以驗證仿射修正 ICCP算法在不同地形特征，不同航跡上提高匹配精度的有效性，航跡匹配結果如圖5(a)、圖5(b)所示。

實驗中的主慣導系統的慣性器件參數和采樣參數如表1。兩塊地形匹配結果統計如表2(a)、表2(b)。

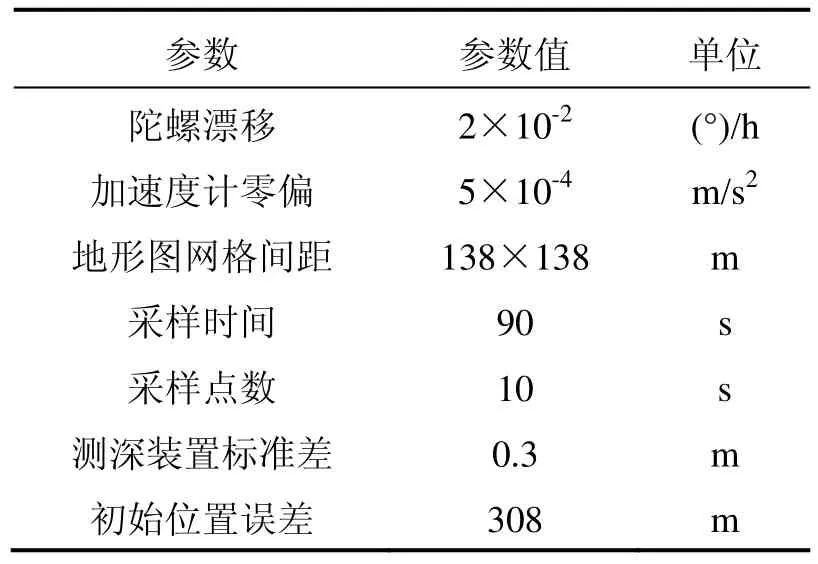
表1 仿真參數Tab.1 Simulation parameters

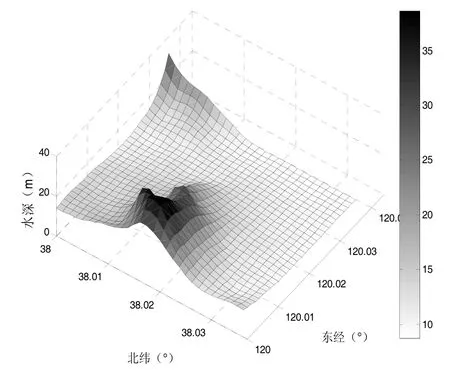
圖4 (a) 仿真實驗所用的地形圖(a)Fig.4(a) Topographic map (a) used in the simulation

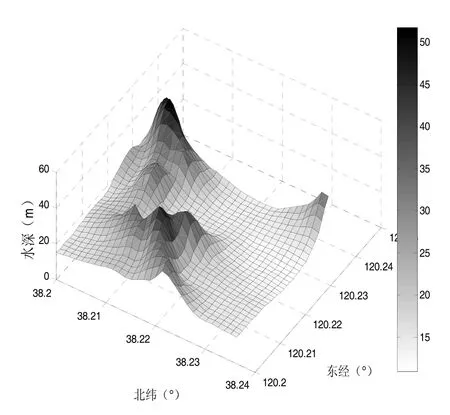
圖4 (b) 仿真實驗所用的地形圖(b)Fig.4(b) Topographic map (b) used in the simulation

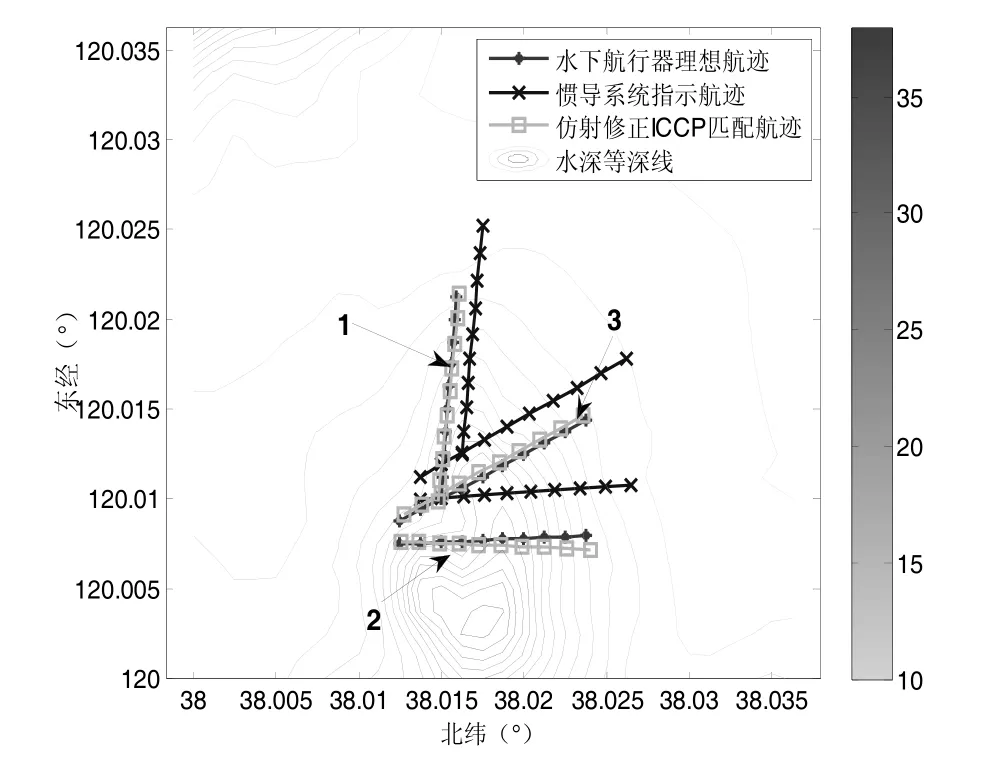
圖5 (a) 水下航行器航跡匹配圖（a）Fig.5(a) Topographic map (a) used in the simulation

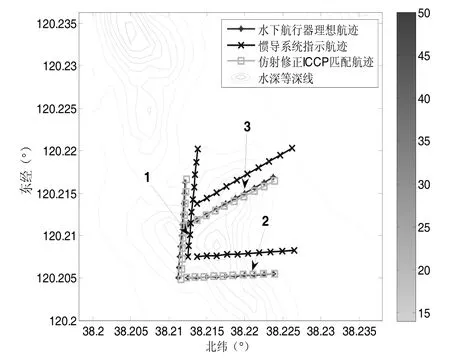
圖5 (b) 水下航行器航跡匹配圖（b）Fig.5(b) Topographic map (b) used in the simulation

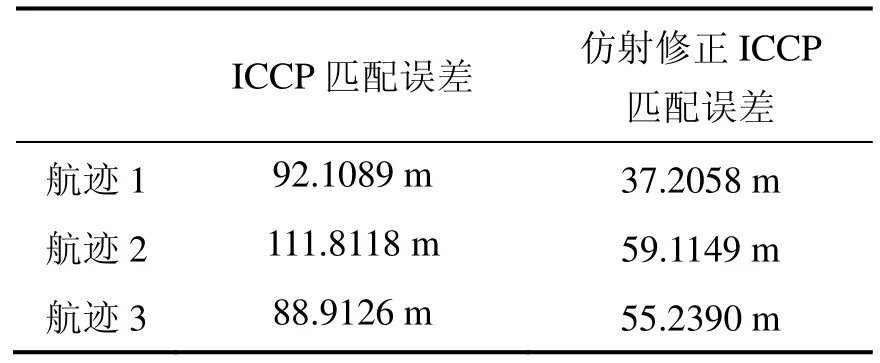
表2 (a) 地形a匹配結果Tab.2(a) Matching results of topographic map a

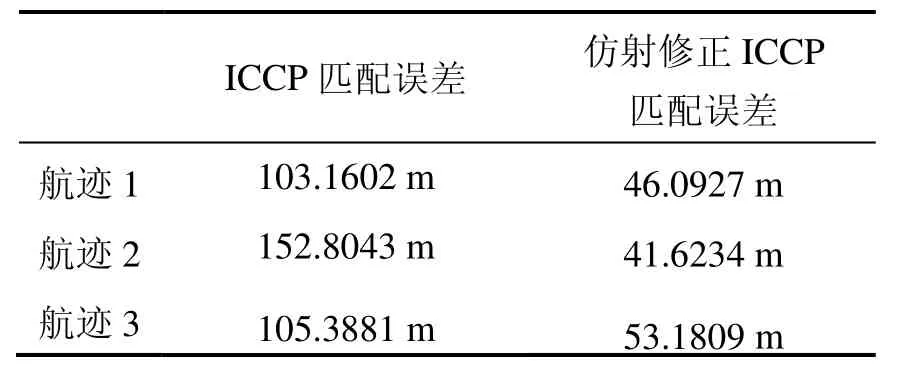
表2 (b) 地形b匹配結果Tab.2(b) Matching results of topographic map b

從地形匹配的結果可以看出：在表1所設置的仿真參數條件下，在地形特征不同的兩個區域，沿三種不同航向的航跡，利用本文所述的仿射修正ICCP匹配方法都能解決ICCP算法僅做旋轉和平移的剛性變換的缺陷。相比于ICCP算法的匹配方法，仿射修正ICCP匹配方法在匹配精度上有很大的提高，同時，由于ICCP匹配航跡已經位于真實航跡附近，仿射修正時無需進行全局最優收斂的判斷，因而運算量較小，一般只需ICCP所耗時間的千分之一。

5 結 論

本文分析了ICCP算法剛性變換的局限性，并針對ICCP算法的局限性，提出了基于仿射修正技術水下地形ICCP匹配導航算法，給出了仿射變換的參數求解方法。通過仿真實驗的驗證了算法在不同地形不同航跡上匹配的有效性，結果表明：基于仿射修正技術的水下地形ICCP匹配算法可以以極小的時間代價來彌補ICCP算法剛性變換的局限性，匹配精度優于ICCP算法，匹配誤差小于數字地圖格網間距的50%。

（References）：

[1]Deng Z,Ge Y,Guan W,et al.Underwater map-matching aided inertial navigation system based on multigeophysical information[J].Frontiers of Electrical and Electronic Engineering in China,2010,5(4):496-500.

[2]童余德，邊少鋒，蔣東方，等.實時ICCP算法重力匹配仿真[J].中國慣性技術學報，2011，19(3)：340-343.TONG Yu-de,BIAN Shao-feng,JLANG Dong-fang,XIAO Sheng-hong.Gravity matching simulation of realtime ICCP algorithm[J].Journal of Chinese Inertial Technology,2011,19(3):340-343.

[3]Bishop G C.Gravitational field maps and navigational errors[J].Oceanic Engineering,2002,27(3):726-737.

[4]劉承香.水下潛器的地形匹配輔助定位技術研究[D].哈爾濱：哈爾濱工程大學，2003.LIU Cheng-xiang.Research on the terrain matching system of the underwater vehicle[D].Harbin:Harbin Engineering University,2003.

[5]Zhou Yingying,Zhang Yanshun,Guo Lei.Simulation of geomagnetic/inertial integrated navigation system[C]//2011 Third International Conference on Measuring Technology and Mechatronics Automation.2011,vol.3:253-256.

[6]Zhang Y,Kang C,Li H,et al.Geomagnetism-aided navigation based on matching algorithm for underwater vehicles[M]//Mechanical Engineering and Technology.Springer Berlin Heidelberg,2012:59-65.

[7]張濤，徐曉蘇，李佩娟.混沌優化水下地形匹配算法研究[J].中國慣性技術學報，2009，17(2)：156-158，164.ZHANG Tao,XU Xiao-su,LI Pei-juan.Underwater terrain matching algorithm based on chaotic optimization[J].Journal of Chinese Inertial Technology,2009,17(2):156-158,164.

[8]羅詩途，任治新.基于仿射模型變換的地磁匹配導航算法[J].中國慣性技術學報，2010，18(4)：462-465.LUO Shi-tu,REN Zhi-xin.Geomagnetic matching algorithms based on affine model[J].Journal of Chinese Inertial Technology,2010,18(4):426-465.

[9]劉穎，吳美平，謝紅衛.地磁匹配算法研究框架和組合匹配策略[J].國防科技大學學報，2010，32(06)：172-176.LIU Ying,WU Mei-ping,XIE Hong-wei.A framework for magnetic matching study and an integrated matching method[J].Journal of National University of Defense Technology,2010,32(6):172-176.

[10]Jiang Z,Chen Z,Zheng B,et al.A kind of 3D reconstructtion method based on affine transformation[C]//2009 3rd International Conference on Genetic and Evolu- tionary Computing.2009:358-361.

[11]Wang K,Li Y,Rizos C.Research on terrain suitability of iterative closest contour point algorithm for underwater navigation[C]//Proceedings of the 22nd International Technical Meeting of the Satellite Division of The Institute of Navigation.2009:866-870.

ICCP algorithm for underwater terrain matching navigation based on affine correction

XU Xiao-su,WU Jian-fei,XU Sheng-bao,WANG Li-hui,LI Pei-juan
(1.Key Laboratory of Micro-inertial Instrument and Advanced Navigation Technology,Ministry of Education,Southeast University,Nanjing 210096,China;2.School of Instrument Science &Engineering,Southeast University,Nanjing 210096,China)

ICCP is the most important matching algorithm used in underwater integrated navigation system.Traditional ICCP algorithm can only do rigid transformation (rotation and translation) for the indicated track of underwater vehicle’s INS.In order to overcome this problem and improve the accuracy of track matching,the error characteristics of INS are analyzed,and the error model of INS is established.Then a new ICCP algorithm based on affine correction is put forward.The track indicated by INS is transformed according to the ICCP algorithm.The affine parameters are solved with the least squares method.The ICCP matching track is modified by affine transformation.The simulations show that the defects of traditional ICCP algorithm can be avoided by affine correction,and the matching result is better than those of traditional ICCP algorithm,in which the matching error is less than 50% of digital map grid spacing.Meanwhile,the additional time consumed in affine correction is just about one thousandth of that in traditional ICCP algorithm.

underwater vehicle;inertial navigation;terrain matching;ICCP;affine transformation

U666.1

A

1005-6734(2014)03-0362-06

10.13695/j.cnki.12-1222/o3.2014.03.016

2014-01-13；

2014-04-15

國家自然科學基金項目（51175082，61203192）

徐曉蘇（1961—），男，博士生導師，從事測控技術與導航定位領域的研究。E-mail：xxs@seu.edu.cn