公鐵合建越江隧道列車運動壓力波數值模擬

桑東升 張旭

公鐵合建越江隧道列車運動壓力波數值模擬

桑東升 張旭

同濟大學機械與能源工程學院

本文采用CFD方法對地鐵通過公鐵合建越江隧道產生的壓力波進行了數值模擬分析。基于國內某公鐵合建越江隧道相關尺寸建立其下部地鐵隧道三維幾何模型，采用動網格方法模擬列車從駛入到駛出隧道的全過程。利用國外模型實驗數據驗證了本文數值模擬方法的可靠性，根據隧道內壓力變化曲線，分析了由于列車通過隧道引起的壓力變化規律。計算得到進入疏散通道防火門處的壓力峰值，最大值1910Pa，最小值-1060Pa，與疏散通道內30～50Pa的正壓有較大的壓力差。

公鐵合建越江隧道壓力波數值模擬動網格

0引言

列車以某一速度進入隧道，由于其對空氣的擠壓和隧道壁面對氣流流動的限制，會在隧道內形成系列的壓縮波和膨脹波，這些波在隧道內的傳播和反射導致隧道內的壓力隨時間不斷變化[1]。列車通過隧道引起的空氣流動通常是復雜的三維非定常、可壓縮、紊態流動[2]，國內外學者采用在線實車試驗、模型模擬試驗、數值模擬計算等方法對列車通過隧道產生的壓力波進行了大量的研究[3～5]。利用數值模擬計算的研究包括利用一維模型對隧道內的壓力波進行數值分析[2，6]，以及對隧道內的壓力波進行三維數值模擬[7～8]。

公鐵合建越江隧道盾構段為雙層隧道，上層為公路隧道，下層為地鐵隧道，兩隧道共用同一疏散通道，地鐵隧道的阻塞比遠大于鐵路山嶺隧道。當上部公路隧道發生火災時，疏散通道開啟，此時下部地鐵隧道正常運行，當列車通過隧道時，地鐵隧道內壓力不斷變化，而疏散通道內維持30～50Pa正壓，因此，地鐵隧道進入疏散通道的防火門兩側的壓力差也將不斷變化。

本文根據國內某公鐵合建越江隧道相關尺寸建立了其下部地鐵隧道的三維幾何模型，利用動網格技術進行數值模擬，得到列車從駛入到駛出隧道即通過越江隧道全過程的壓力變化曲線。本文根據國外縮尺模型實驗進行驗證，模擬結果與實驗結果比對吻合較好，確認計算方法準確可靠后，分析列車通過隧道引起隧道內的壓力變化規律，以及壓力峰值隨隧道長度的變化。

1研究方法

1.1模擬場景設置

公鐵合建越江隧道上部公路隧道發生火災時，此時公路隧道和地鐵隧道共用的疏散通道開啟，地鐵隧道側的防火門關閉，下部地鐵隧道正常運行，假設列車從大氣駛入隧道，通過隧道后駛入大氣，模擬列車通過下部地鐵隧道過程中，地鐵隧道內的壓力變化。

1.2幾何模型

根據國內某在建公鐵合建越江隧道相關尺寸建立其下部地鐵隧道的幾何模型，如圖1所示，隧道截面為4.5m×4.5m；列車長120m，寬3m，高3.8m，隧道阻塞比約為0.56，時速80km/h，設定隧道內線路為直線，忽略隧道坡度，列車的頭尾部均為鈍體，車頭與車體夾角為90°，假設列車勻速通過隧道。

圖1幾何模型示意圖

隧道達到一定長度后，壓力波動絕對值不再隨著隧道長度的增加而增大[1]，故不考慮隧道長度對于壓縮波的非線性效應，取隧道長度1000m。為保證計算結果的精確性，車頭前端點初始位置距離隧道入口100m，外場大氣高度為50m，寬度100m，長度300m。

忽略橫向風作用，流場沿列車的對稱面對稱，為有效地縮短模擬的時間，模型只按照對稱面建立左半部分。

1.3數值方法

列車通過隧道引起的空氣流動流場雷諾數Re大于1×106，流動處于紊流狀態，三維非穩態流場的模擬采用CFD軟件FLUENT完成，并采用連續性方程、雷諾時均N-S方程和RNG k-ε模型進行求解，壓力與速度的耦合運用PISO算法，壓力離散格式為PRESTO，3個坐標方向的速度方程和k、ε方程的對流項離散采用二階迎風差分格式。

通常由于列車的運行速度較低，馬赫數小于0.3，可以按照不可壓縮粘性流體處理，但是列車通過隧道過程中，空氣受到強烈擠壓，不可以忽略空氣的壓縮性，故空氣按可壓縮氣體計算。

1.4動網格模型和邊界條件

采用動網格技術模擬列車通過隧道的過程。在FLUENT中有三種方法可以定義動邊界：彈性光順、鋪層和局部重構法。考慮到列車通過隧道的特征，本文選取鋪層方法進行模擬[9]。計算區域劃分如圖2所示，計算流場分為固定區域和移動區域，兩區域通過滑動交界面連接，在流體移動區域，將列車以及列車相連的前后流場區域設置為移動剛體，即列車周圍的網格不發生變化，隨著列車一起運動；流場區域兩端的網格被拉伸和壓縮，從而根據網格的尺寸大小不斷的消失和生成。隨著列車運行，在每個時間步長內模擬軟件自動調整網格計算得到動態結果。

圖2動網格計算區域劃分

在本文計算流場中，隧道入口的流場區域邊界設定為壓力入口邊界條件，隧道出口的流場區域邊界設定為壓力出口邊界條件，對稱面設為對稱邊界條件。列車壁面、隧道壁面和地面均采用無滑移壁面邊界條件，采用標準壁面函數計算壁面附近流場。

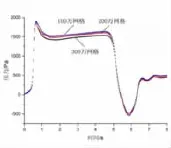
圖3網格獨立性檢驗測試結果對比圖

網格劃分采用結構化六面體網格，分別取總數為100萬、200萬和300萬的3組網格進行模擬比較。圖3對比了隧道內距離隧道入口200m處的前8秒內壓力隨時間變化的曲線。由圖3可知，三組網格的模擬得到的壓力變化趨勢基本一致，100萬網格計算得到的壓力與其他兩組網格計算結果的誤差值在10%以內，在工程可接受的范圍內。考慮動網格計算時間較長，為節省計算時間，選用100萬網格模型進行計算。

非穩態計算最大時間步長由最小網格尺度和列車的運行速度決定，為保證動網格更新后的網格質量，同時考慮計算時間，時間步長取為0.005s。

1.5計算方法驗證

Ricco P等人[3]開展了一系列模型實驗研究列車通過隧道產生的壓力波，本文選用其中一組實驗進行驗證。圖4為模型實驗原理圖（Ricco P等[3]），隧道模型為圓柱體，長6m，直徑99mm；列車模型斷面形狀為正方形，長600mm，邊長33.7mm；隧道阻塞比約為0.1475。列車在沿著隧道軸線兩根平行的鋼絲繩上運行，最大速度為150km/h（42m/s），本組實驗列車通過隧道的速度為110km/h（30.6m/s）。壓力傳感器安裝在距離隧道入口17mm，300mm，600mm和900mm處，測試頻率最高為40kHz。

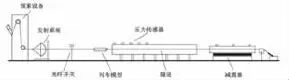
圖4模型實驗原理圖

圖5給出了Ricco P等人由實驗測得的在距離隧道入口900mm處的壓力隨時間變化的曲線與本文數值模擬所得結果的對比。可以看出，模擬得到的壓力隨時間變化趨勢與實驗結果基本一致，并且壓力的最大值和最小值都與實驗結果吻合較好，相對誤差在2%以內。可以認為本文中模擬列車通過隧道產生壓力波的方法可靠。

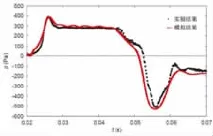
圖5模擬結果與實驗結果對比

2模擬結果與分析

根據地鐵隧道內進入疏散通道防火門的位置，沿隧道長度方向每隔150m布置一處壓力測點。圖6所示為距離隧道入口300m、600m和900m三處測點地鐵駛入隧道壓力變化曲線。可以看出三個測點壓力變化的最大值和最小值比較接近，到達最大值的時刻分別為0.97s、1.87s、2.75s，各時刻之間的間隔大致為0.9s，各測點之間的距離為300m，可以計算得到壓力波傳播的速度為300m/0.9s≈333m/s，近似等于聲速。

圖6隧道長度方向上測點的壓力變化曲線

圖7所示為地鐵從駛入隧道到駛出隧道整個過程中，距離隧道入口150m和450m兩處測點壓力隨時間的變化過程。當列車駛入隧道時，形成壓縮波，導致隧道內壓力驟增，隨著列車進一步駛入，壓縮波強度不斷增大；壓縮波以聲速沿隧道向前傳播，到達隧道出口時，以膨脹波的形式反射回來沿隧道向進口方向傳播。當列車尾部一進入隧道，由于列車尾部的壓力低于隧道口大氣壓，產生膨脹波，也以聲速向隧道出口方向傳播，傳播到列車頭部時，部分膨脹波以壓縮波形式反射回去，另一部分仍以膨脹波的形式繼續向出口方向傳播，傳到隧道出口時，又以壓縮波形式反射回來。所以壓縮波和膨脹波在隧道內多次反射和傳播，并且互相疊加，導致隧道內的壓力隨時間不斷變化。

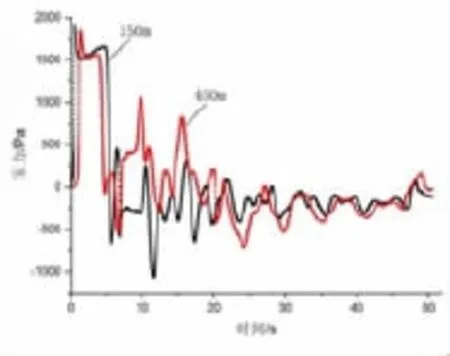
圖7地鐵通過隧道壓力變化過程

由圖7也可以看出由于摩擦，壓縮波和膨脹波在傳播的過程中逐漸衰減。雖然列車通過隧道過程中，隧道內的壓力隨時間不斷變化，但是隧道內不同位置的壓力變化規律相同，僅僅作用時間和幅值大小不同。

分析距離隧道入口150m處壓力隨時間變化曲線，在前1.5s內壓力驟增后又下降是由于車頭與車體之間夾角超過30°，車頭附近出現氣流分離的結果[3]。在6.75s時壓力驟降，原因是此刻列車通過該測點，導致測點處的壓力下降，當列車尾部通過測點時，壁面壓力上升。而在47.55s時出現壓力上升，是由于當列車頭部駛出隧道時，產生的壓縮波以音速傳播到測點導致隧道壁面的壓力迅速上升，隨著列車駛出隧道，隧道內壓力下降。

圖8所示為不同測點處測得的壓力最大值和最小值，由于壓力波傳遞過程中的摩擦，造成沿隧道長度方向壓力波峰值逐漸減小。模擬計算得到測點處的壓力最大值為1910Pa，最小值為-1060Pa。這與疏散通道內由風機維持30～50Pa的正壓有較大的壓力差。

圖8不同測點處壓力最大值和最小值

3結論

1）采用動網格技術對列車通過隧道產生的壓力波進行數值模擬計算，利用國外模型實驗驗證，計算結果與實驗結果吻合較好，驗證計算方法準確可靠；得到了列車從駛入到駛出隧道通過隧道的全過程中，隧道內不同位置處壓力隨時間變化的曲線。

2）分析了由于列車運動引起的隧道內的壓力變化規律，可以計算得出空氣動力學效應產生的壓縮波和膨脹波在隧道內基本以聲速傳播；列車通過隧道過程中，隧道內不同位置的壓力變化規律相同，僅作用的時間和幅值大小不同。

3）模擬得到進入疏散通道防火門處的壓力峰值，沿隧道長度方向逐漸減小；最大值為1910Pa，最小值為-1060Pa，與防火門另一側疏散通道內30～50Pa的正壓有較大的壓力差。

[1]田紅旗.列車空氣動力學[M].北京:中國鐵道出版社,2007

[2]梅元貴，趙海恒，劉應清.高速鐵路隧道壓力波數值分析[J].西南交通大學學報,1995,(6):667-672

[3]Ricco P,Baron A,Molteni P.Nature of pressure waves induced by a high-speed train travelling through a tunnel[J].Journal of Wind Engineering and Industrial Aerodynamics,2007,95(8): 781-808

[4]Ko Y,Chen C,Hoe I,et al.Field measurements of aerodynamic pressures in tunnels induced by high speed trains[J].Journal of Wind Engineering and Industrial Aerodynamics,2012,100(1): 19-29

[5]Raghunathan R S,Kim H D,Setoguchi T.Aerodynamics of highspeed railway train[J].Progress in Aerospace Sciences,2002,38 (6):469-514

[6]吳明.基于一維流動模型的高速列車隧道壓縮波特性研究[D].蘭州:蘭州交通大學,2013

[7]Uystepruyst D,William-Louis M,Creusé E,et al.Efficient 3D numerical prediction of the pressure wave generated by high-spee -d trains entering tunnels[J].Computers&Fluids,2011,47(1): 165-177

[8]Ogawa T,Fujii K.Numerical investigation of three-dimensional compressible flows induced by a train moving into a tunne[J].Computers and Fluids,1997,26(6):565-585

[9]Huang Y,Gao W,Kim C.A numerical study of the train-induced unsteady airflow in a subway tunnel with natural ventilation ducts using the dynamic layering method[J].Journal of Hydrodynamics (Ser.B),2010,22(2):164-172

Num e ric a l Sim ula tion on Pre s s ure Wa ve s Induc e d by a Tra in Tra ve lling Through a Roa d a nd Subw a y Com bine d Tunne l

SANG Dong-sheng,ZHANG Xu
School of Mechanical Engineering,Tongji University

A numerical simulation on pressure waves generated by a train travelling through a road and subway combined tunnel was carried out by means of the Computational Fluid Dynamics（CFD）method.The three-dimensional model of subway was establishedbased on an under construction tunnel in China.Dynamic mesh method was applied to simulate the process of a train entering and running through the tunnel.The numerical simulation method was validated against a scaled model experiment.The pressure change induced by a train travelling through the tunnel was analyzed according to the pressure curve.Peak pressure at the fire door where to enter the fire evacuation routes was calculated. The maximum(1910Pa)and the minimum(-1060Pa)pressure could be dozens of times larger than that(30～50Pa)in the evacuation routes.

road and subway combined tunnel,pressure waves,numerical simulation,dynamic mesh

1003-0344（2014）05-023-4

2013-8-18

張旭（1955～），男，博士，教授；上海市同濟大學機械與能源工程學院（201804）；E-mail:xuzhang@tongji.edu.cn