基于非線性理論的2K-V型減速機動力學建模技術

韓林山 閃修洋

（華北水利水電大學機械學院，河南 鄭州 450011）

基于非線性理論的2K-V型減速機動力學建模技術

韓林山 閃修洋

（華北水利水電大學機械學院，河南 鄭州 450011）

以2k-v型減速機為研究對象，利用等價力學模型的方法，考慮各零件的制造誤差、轉矩、間隙、慣性載荷和接觸變形等因素的作用，對2k-v型減速機的關鍵零件進行了受力分析，并根據D'Alembert原理，建立了該傳動系統動態傳動精度的非線性動力學模型。

2k-v型減速機；誤差因素；非線性動力學模型

2k-v型傳動裝置是一種新穎的擺線針輪傳動機構，具有傳動精度高、傳動比大、傳動效率高、抗沖擊能力強、剛度大、回差小等特點，廣泛應用于印刷機械、機器人、自動化設備、起重運輸、石油化工等領域。2K-V型減速機傳動系統結構圖如圖1所示。

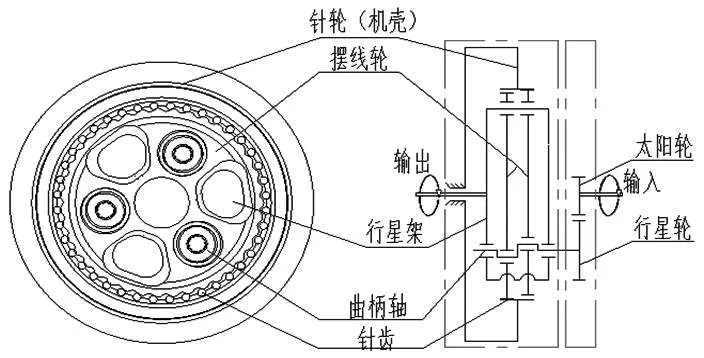
圖 1 2K-V型減速機傳動系統簡圖

日高照晃教授[1-3]通過建立質量彈簧等價模型來分析和研究2k-v型傳動機構的動態傳動精度；國內學者對該傳動系統的傳動精度的研究僅限于靜態或幾何領域，本文在充分分析2k-v型減速機的組成結構、工作原理及傳動特點的基礎上，在考慮制造誤差、間隙、轉矩等因素的影響下，對其受力情況進行了全面的分析，從動力學的角度建立了動態傳動精度的數學模型。

1 建立質量彈簧等價模型

本文所研究的2k-v型減速機包括1個太陽輪、3個行星輪、3個曲柄軸、2個擺線輪、針輪和行星架等。

由于擺線針輪系統中存在齒輪嚙合間隙、零件加工誤差、零件彈性變形和軸承間隙等影響因素，導致零件質心的實際位置位置及其轉角與理想位置產生了偏差。根據日高照晃的相關研究，通過線位移、角位移來表示理想位置與實際位置的偏差，并把這些線位移、角位移都叫作微位移。研究減速機動態傳動精度的力學模型如圖2所示。由于擺線針輪傳動裝置的各零件在制造和裝配環節中存在齒輪嚙合間隙、加工誤差、軸承間隙及零件彈性變形等影響因素的存在，在受力分析中零件的相對轉角及實際質心位置都會與其理想位置發生偏差。在2K-V傳動系統受力研究中，將各零件的彈性變形、制造誤差，裝配誤差和軸承間隙等影響因素統一到一個質量彈簧等價模型中。在這個質量彈簧等價模型中，每個元件看作一個剛體，并用彈簧表示各個零件之間的接觸強度，那么各個零件的裝配誤差、制造誤差、間隙及微小位移等都可以換算到等價彈簧上，稱之為“等價誤差”。這樣，通過等價誤差和等價彈簧就可以表示出個零件上的力。各零件間的剛度系數，如太陽輪與行星輪間的嚙合剛度系數kj、行星架與針輪間的軸承支承剛度系數kca、曲柄軸與擺線輪軸孔間的軸承支承剛度系數kji、針齒與擺線輪間的嚙合剛度系數kjk和太陽輪的支承剛度系數ks、曲柄軸和行星架軸孔間的軸承支承剛度系數kbi，其中ki通過輪齒彎曲變形來確定[4]，ks采用計算太陽輪軸的彎曲變形求得，而kji、kbi、kca、kjk采用Palmgren公式[5]確定。

其次是相關的靜、動坐標系的確定方法。把固定針輪中心O設為原點，與其軸線垂直的斷面設為平面靜坐標系（x，y）；從太陽輪端即輸入端開始，依次對兩個擺線輪進行編號j=1，2，并把擺線輪的理論質心Oj設作原點，以擺線輪的偏心方向為ηj軸，以其公轉角方向轉動90°做ξj軸，建立擺線輪的動坐標系（ηj，ξj）。在建模過程中，設定擺線輪j=1的ηj軸的初始位置與靜坐標系x軸方向一致。同時，在動力學模型中，將各等價彈簧安置在各零件輪齒嚙合處或坐標軸的正方向接觸處，且設定各因素使彈簧受拉為正，受壓為負；?i表示擺線輪上的曲柄軸軸孔的相對位置，取?i=2π（i-1）/3，i=1，2，3，ψj表示兩擺線輪的理論質心Oj的相對位置，取ψj＝（j-1）π（j=1，2）。

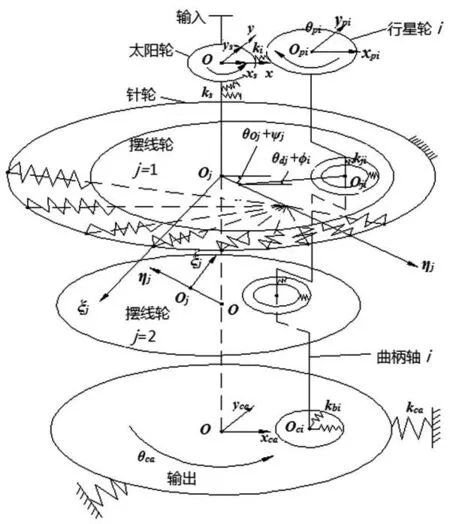
圖 2 2k-v型減速機動態傳動精度計算的力學模型

2 各零件的受力分析

2.1 太陽輪的受力分析

太陽輪的受力情況如圖3所示。圖中，ωs為太陽輪的自轉方向，xs、ys為太陽輪的微位移，Rsx、Rsy、Rgi為由于轉矩Ts的作用在O處及嚙合處產生的作用力；Fsx、Fsy、Fspi為由于太陽輪和第i個行星輪的基園偏心誤差（Es，βs）、（Epi，βpi）和太陽輪的裝配誤差（As，γs）的影響在O處及嚙合處產生的彈性力。

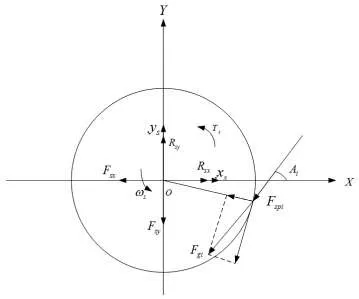
圖3 太陽輪的受力

設esx、esy為裝配誤差（As，γs）在支承處x、y方向上所產生的位移。其大小為：esx=Ascosγs，esy=Assinγs。

則Fsx=ks（xs-esx） Fsy=ks（ys-esy）

設Si為微位移xs、ys在嚙合處產生的位移，si=xscosAi+yssinAi；Spi為行星輪的微位移xpi、ypi、θpi-θp在輪齒嚙合處產生的位移Spi=-xpicosAi-ypisinAi-Rbp（θpi-θp）；

esi、epi為太陽輪基圓偏心誤差在嚙合處產生的位移

esi=-Escos（θs+βs-Ai），epi=Epicos（βpi-θp-Ai）

則：Fspi=ki（Si+Spi+esi+epi）

Fgi=TS/3rsb（rsb為太陽輪的基圓半徑）

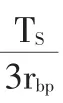
2.2 擺線輪的受力分析

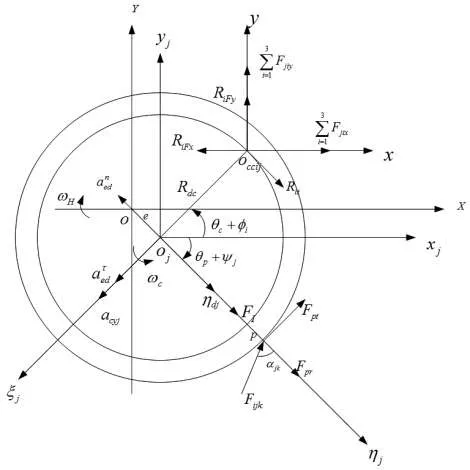
圖 4 擺線輪的受力

令擺線輪的3個微位移分別為ηdj、θdj-θc和θoj-θp，其中ηdj表示擺線輪的線微位移，θdj-θc表示擺線輪的自轉角微位移，θoj-θp表示擺線輪的公轉角微位移。

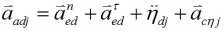
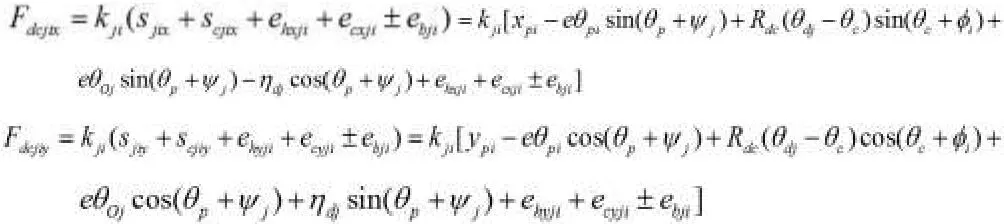
式中±號是依據擺線輪與曲柄軸接觸處的變形量大小進行確定。

④Fijk是由于誤差、間隙等因素產生的擺線輪輪齒與針齒間的作用力Fijk=kjk(Sjk+eRk+ePk+eRjk+ePjk+ej+ejk)。

式中，Sjk是擺線輪的3個微位移在輪齒嚙合處所產生的位移

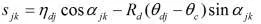
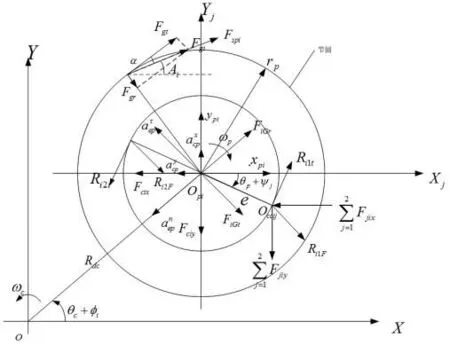
圖 5 曲柄軸及其固聯的行星輪的受力

eRK是針輪齒槽偏差RK所引起的位移eRk=-Rkcos(αjk-?jk)

式中，αjk是第kr個針齒的中心與第j個擺線輪的節點連線和ηj軸正方向和ηj軸正方向間的夾角（°），其中kr=1，2，…Zr；?jk——第j個擺線輪ηj軸正方向和第kr個針齒半徑方向之間的夾角（°）。

epk是針輪在其圓周方向具有的齒距累積偏差Pk所產生的位移eRk=-Rkcos（αjk-?jk）

eRjk是擺線輪齒槽具有的偏差Rjk產生的位移eRjk=Rjkcos(αjk-?djk)式中，?djk是第kr個針齒中心與第j個擺線輪的中心連線和軸ηj正方向之間的夾角。

epjk是擺線輪齒距累積偏差pjk產生的位移ePjk=Pjksin(αjk-?djk)。

2.2 曲柄軸及其固聯的行星輪的受力分析（見圖5）

①圖中，Rit、RiF為擺線輪對曲柄軸承的作用力Ri的兩個分力，與上文的擺線輪受力中的曲柄軸對擺線輪的力是一對作用力與反作用力，這里不再詳細介紹。

④設Sbix、Sbiy是行星架的三個微位移xca、yca和θca-θc在曲柄軸支承處x、y方向上產生的位移；Six、Siy是行星輪的微位移xpi、ypi和θpi-θp在行星架接觸處x、y方向上產生的位移；ecaxi、ecayi是行星架的曲柄軸孔偏心誤差為（Ecai，βcai）在x、y方向上所產生的位移；exi是行星架上的曲柄軸孔處的軸承間隙δxi在支承處產生的位移，則由于誤差等因素的作用產生的行星架與曲柄軸接觸處x、y方向上的作用力：

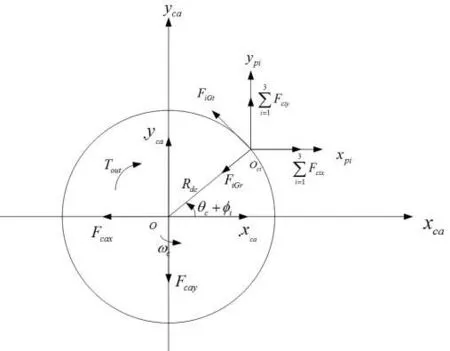
圖 6 行星架的受力圖

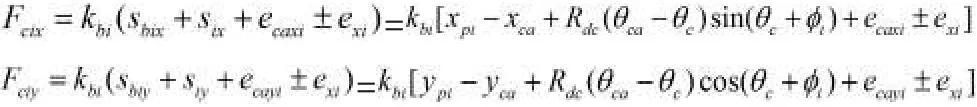
式中±號是根據行星架與曲柄軸接觸處的變形量多少來確定。

其具體判斷方法為：若Sbix+Six+ecaxi≥-exi，取+號；若Sbix+Six+ ecaxi≤exi，取-號；若-exi≤Sbix+Six+ecaxi≤exi，表明行星架曲柄軸孔處沒有接觸載荷即Fcix、Fciy的值為零。

2.3 行星架的受力分析

行星架的受力如圖6所示，由于建模時傳動系統是垂直放置的，所以不考慮由于重力而使行星架所受得支承力。

設行星架的三個微位移為xca、yca和θca-θc，其在殼體支承處x、y方向上產生的位移分別為：Scax=xca,Scay=yca

行星架與減速機殼體間的軸承間隙為δca，則其在支承處所產生的位移為：eca=-δca

綜上所述，由于誤差的影響使行星架殼體支承處x、y方向上產生的作用力為：Fcax=kca(Scax-ecx±eca)=kca(xca-ecx±eca)

Fcay=kca(Scay-ecy±eca)=kca(yca-ecy±eca)

式中±號是依據行星架殼體支承處變形量的大小來確定。具體判定方法為：若Scax-ecx≥-eca，取+號；若Scax-ecx≤-eca，則去-號；若-eca≤Scax-ecx≤eca，表明行星架殼體支承處沒有接觸載荷，即Fcax、Fcay的值為零。

3 系統動力學模型的建立

首先對零件處于理想位置時進行受力狀況，然后根據D'Alembert原理建立動態傳動系統的動力學模型。

在動力學建模過程中，特別考慮了行星輪、擺線輪及曲柄軸的科氏加速度，系統中的摩擦阻力給予忽略。在嚙合過程中，由于輪齒的加工誤差、間隙、裝配誤差以及微位移的作用，其嚙合力的方向都會與其理想的嚙合方向產生偏移，但是，考慮這些作用都比較小，所以在建模時，可以按照在理想狀態時的行星齒輪機構確定其嚙合力作用方向，從而忽略嚙合力方向的細微改變。

經過整理，2k-v型傳動系統的動態傳動精度動力學模型為：

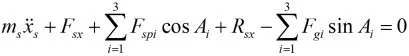
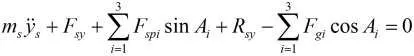
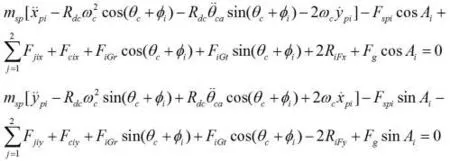
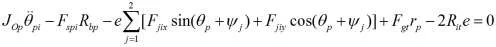
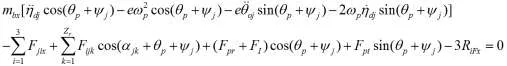
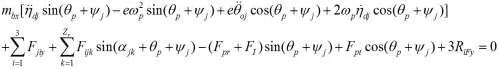
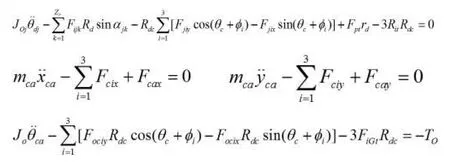
式中:ms——太陽輪質量（kg）

msp——曲柄軸及行星輪的質量總和（kg）

mbx——擺線輪質量（kg）

JOP——曲柄軸及行星輪轉動慣量（kg·m2）

JOj——擺線輪的轉動慣量（kg·m2）

ωc——行星架的理論轉動角速度（rad/s）

ωP——行星輪理論自轉角速度（rad/s）

TO——外界負載轉矩N·m

式中M、C、K分別為質量矩陣、阻尼矩陣和剛度矩陣，矩陣階數均為20×20；X為位移向量

X=（xs，ys，xp1，yp1，θp1，xp2，yp2，θp2，xp3，yp3，θp3，ηd1，θo1，θd1，ηd2，θo2，θd2，xca，yca，θca）；Q是廣義力矢量。

由于剛度系數kji，kbi，kca，kjk可以用位移的函數表示，而且存在間隙，所以該系統式非線性的。

4 結語

本文在2K-V型減速機的工作原理及傳動特性的基礎上，對2K-V型傳動系統典型零部件做了全面的力學分析。考慮各零件的制造誤差、裝配誤差、轉矩、間隙和彈性變形等因素時的受力情況，利用彈簧“等價模型”方法，建立了雙擺線輪、三曲柄、圓盤式輸出類型2K-V型減速機的彈簧等價力學模型，為提高2K-V的綜合性能等方面的研究打下了基礎。

[1]日高照晃ほか.サイクロイド齒車を用ぃたK-H-V形遊星齒車裝置の回轉傳達誤差に開する研究（第1報，解析方法）.日本耭械學會論文集（C編），Vol.60，No.570，1994.

[2]石田武ほか.サイクロイド齒車を用ぃたK-H-V形遊星齒車裝置の回轉傳達誤差に開する研究（第2報，各種加工誤差、組立誤差が回轉傳達誤差に及ほす影響）.日本耭械學會論文集（C編），Vol.60，No.578，1994.

[3]石田武ほか.サイクロイド齒車を用ぃたK-H-V形遊星齒車裝置の回轉傳達誤差に開する研究（第3報，各種誤差にほす相互影響）.日本耭械學會論文集（C編），Vol.60，No.578，1994.

[4]李潤方，王建軍.齒輪系統動力學[M].北京：科學出版社，1997.

[5]丁長安（導師：朱均，周福章）.滾動軸承-主軸系統靜動特性研究[D].西安：西安交通大學，2003.

[6]李充寧，孫濤，劉繼巖.2k-v型行星傳動的結構和力的分析[J].機械傳動,2000（2）：7-9.

[7]鄭州工學院機械原理及機械零件教研室.擺線針輪行星傳動[M].北京：科學出版社，1978.

[8]韓林山（導師：沈允文）.2K-V型擺線針輪系統動態傳動精度的研究[D].西安：西北工業大學，2008.

TH132.4

A

1671-0037（2014）12-97-4

韓林山（1964-），男，工學博士，教授，研究方向：機械設計及理論研究。

閃修洋（1989-），男，在讀研究生，研究方向：機械設計及理論。