有效預應力空間分布確定方法

雷 宇

(上海市政工程設計研究總院(集團)有限公司，上海 200092)

預應力混凝土大型箱梁結構的整體抗裂性是一個相當復雜的問題，開裂是普遍現象。從受力上分析箱梁開裂的原因，發現常規設計的不足，明確常規設計的可靠性，對設計方法的改進具有重要意義。目前國內設計規范對箱梁橋設計主要是采用全截面的平截面假定，利用基于平面桿系的有限元方法求解，并通過一個內力增大系數計入箱梁橫截面扭轉翹曲、剪力滯、畸變的效應。這種方法對于箱梁尤其是跨徑較大的箱梁結構是不合適的。因此，為了確保設計的安全性、合理性和耐久性，有必要對預應力混凝土連續剛構橋的空間受力特性和配筋方法進行分析，為橋梁抗裂性設計提供依據［1］。

1 預應力施加的模擬方法

預應力施加的模擬方法通常為初應變法和降溫法，都是通過在力筋模型中產生拉應變來等效力筋被張拉時所產生的拉應變。初應變法是通過定義材料的初始屬性來實現所需的拉應變，降溫法是通過施加溫度荷載來實現所需的拉應變。彈性分析時二者本質相同，非線性分析時存在差異。初應變法一般不考慮預應力損失，否則每個單元的實常數各不相等，建模工作量較大;降溫法根據有效預應力的分布對各力筋單元施加相應的降溫值，工作量相對較小。故對于大型箱梁結構，采用降溫法更為適宜。

降溫法的原理是利用溫度變化產生的線應變等于軸力產生的線應變，即。則所需降溫值，其中，Δt為所需施加的降溫值;A為預應力筋截面面積;α為預應力筋線膨脹系數;E為預應力筋彈性模量。

能夠反映預應力損失是降溫法的優點，但確定有效預應力的分布卻是難點。由于大型箱梁結構中預應力筋數量眾多，線形復雜，使得計算各項預應力損失及考慮反摩阻的影響較為困難。鑒于這點，常規辦法是采用折減系數來考慮預應力損失，但有效預應力值沿長度不變，這與實際相差較大［2］。針對上述不足，本文提出引入平面桿系計算結果來準確確定力筋中的有效預應力分布。即建立與實體模型完全相同的平面桿系模型，精確算出各項預應力損失。由于實體模型能夠考慮徐變收縮引起的預應力損失，故計算有效預應力時只需考慮摩擦損失、錨具變形和預應力筋回縮引起的損失、混凝土彈性壓縮引起的損失及預應力筋松弛引起的損失。需要說明的是，預應力筋松弛引起的損失是隨時間發展的，模型難以模擬，故簡化為一次性扣除。下面以某連續剛構為背景工程，將上述兩種方法進行對比分析。

2 實例分析

2．1 連續剛構構造

該橋為雙薄壁墩連續剛構橋，跨徑140 m+268 m+140 m=548 m。主梁為分離式單箱單室直腹板箱梁，單幅箱梁頂寬16．4 m，梁底寬7．5 m。箱梁梁高及底板厚度均按1．6次拋物線變化。橋墩處梁高15．0 m，跨中梁高4．5 m。主梁采用三向預應力體系:縱、橫向預應力采用鋼絞線，豎向預應力采用精軋螺紋粗鋼筋。主梁采用C60混凝土。主梁一般構造見圖1［3］。

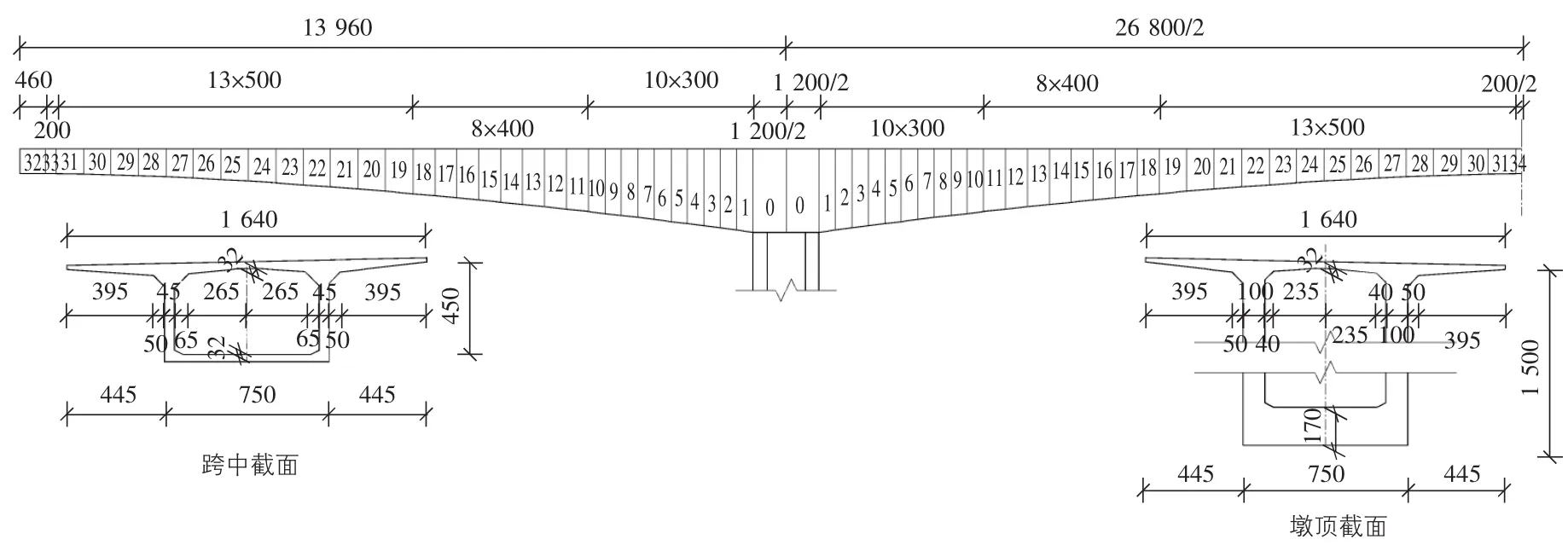
圖1 主梁一般構造圖

2．2 有限元模型

計算分析采用MIDAS有限元分析程序。實體模型和平面桿系模型說明如下。1)平面桿系模型。依據施工過程，進行平面桿系模型的單元劃分。主梁與墩身采用剛性連接。模型的邊界條件符合實際情況，雙薄壁墩的墩底采用固定約束，邊支座采用單向約束。2)空間實體模型。由于只分析永久作用，利用結構的對稱性，選取縱向1/2結構建立空間實體單元和梁單元組合的有限元模型，模擬真實的懸臂澆筑施工過程。中跨混凝土箱梁采用8節點的實體單元模擬，少量位置采用6節點實體單元模擬，邊跨混凝土箱梁采用梁單元模擬。在薄壁墩處實體單元和梁單元連接的地方，設一塊大剛度零重量的虛擬剛性板。縱向、豎向以及橫向預應力筋采用梁單元模擬，預應力效應通過降溫法模擬。引入平面桿系模型的計算結果確定有效預應力分布。模型的邊界條件符合實際情況，雙薄壁墩的墩底采用固定約束，邊支座采用雙向約束，中跨跨中采用縱向對稱約束。圖2和圖3分別為空間實體有限元模型和幾何模型的示意圖。

圖2 空間實體有限元模型示意圖

圖3 空間實體幾何模型示意圖

2．3 兩種方法的對比分析

1)鋼束有效預應力值差異。結構中F31號預應力筋長度最大，線形最復雜，有效預應力值分布變化最大，故以其進行有效預應力值比較。圖4，圖5分別給出了兩種方法在成橋初期和成橋30年兩個階段鋼束中有效預應力的比較。圖中標注C的曲線表示采用常規折減系數法的計算結果，標注X的曲線表示采用引入平面桿系計算結果方法的計算結果。由圖4，圖5不難看出兩種方法下鋼束中有效預應力存在著明顯差異，且這種差異隨著遠離張拉端而逐漸增大。表1給出了這種差異的具體值。

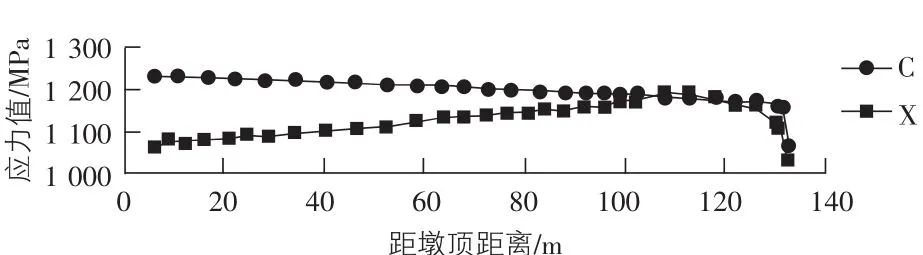
圖4 成橋初期鋼束應力值比較示意圖

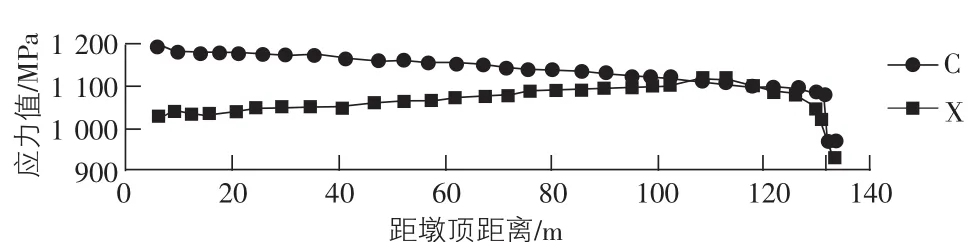
圖5 成橋30年鋼束應力值比較示意圖

從圖4，圖5以及表1可以看出兩種方法計算得到的鋼束有效預應力值存在著很大的差異，采用常規折減系數法得到的鋼束有效預應力值與實際情況有較大的差異，這種差異應引起重視。

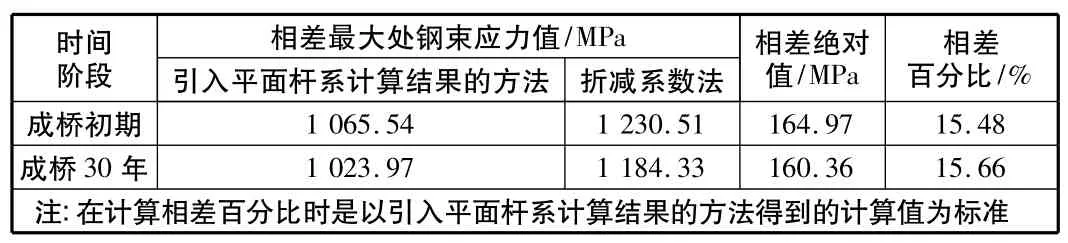
表1 鋼束有效預應力最大差值比較

2)結構受力特性差異。通過比較關鍵截面的應力來說明。關鍵截面選取跨中截面和薄壁墩外側截面進行對比。圖6，圖7給出了兩種計算方法得到的上述兩截面的法向應力云圖(限于篇幅這里只給出成橋初期應力云圖，其中a)為引入平面桿系計算結果的方法，b)為常規折減系數法)。

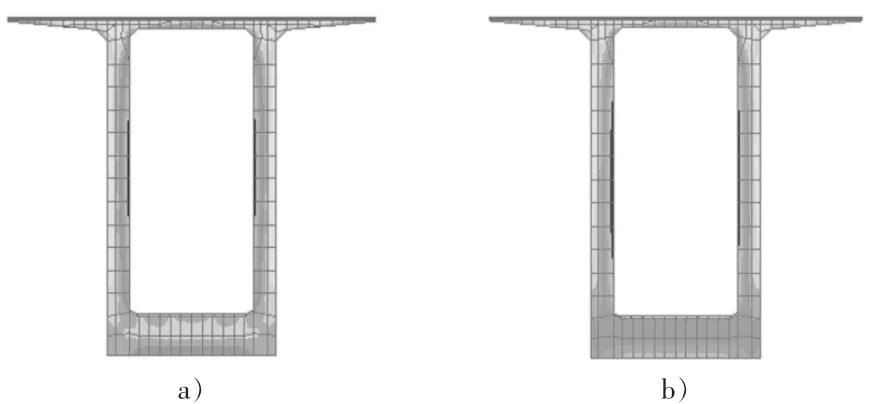
圖6 薄壁墩外側截面成橋初期法向應力云圖

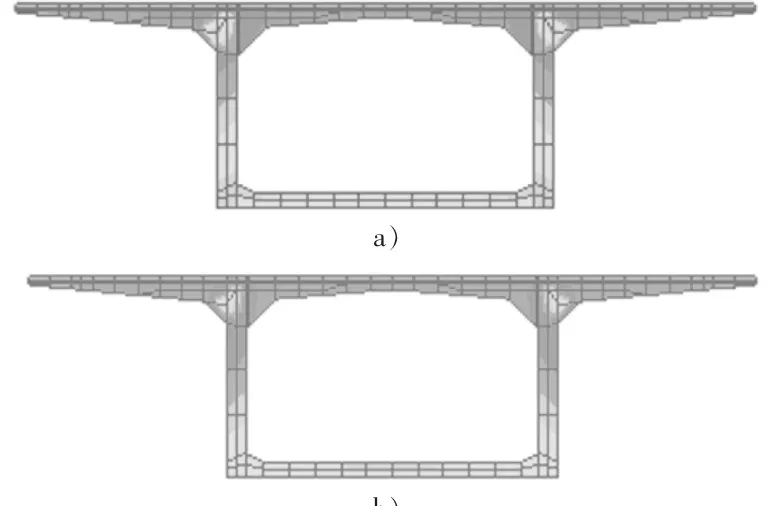
圖7 跨中截面成橋初期法向應力云圖

由圖6，圖7可以看出兩種方法得到的應力云圖存在明顯差異，應力值相差較大，應力分布規律也完全不同。以薄壁墩外側截面成橋初期法向應力為例:a)方法得到的截面法向應力為－4．39 MPa～ － 17．68 MPa，b)方法得到的截面法向應力為－5．16 MPa～ －20．28 MPa;底板內應力分布，a)呈環狀分布，中心約為 12．5 MPa，外圍約為 11．04 MPa，b)分布比較均勻，約為9．36 MPa，僅在最下緣有很小一部分約為7．36 MPa。

3 結語

通過上述對比分析，可以看出常規折減系數法與實際情況存在較大的差異，且這種差異較難減小到可接受的范圍內，因此對于大型箱梁結構的空間分析采用折減系數法是不妥當的。本文提出的引入平面桿系計算結果的方法修正上述不足，真實反映了鋼束中有效預應力的分布，準確反映了預應力對結構的空間效應。該方法建模工作量增加不大，但結果精確度有較大提高。需要說明的是，本文在采用引入平面桿系計算結果的方法時，平面桿系模型的單元劃分是依據懸臂施工的節段長度而定的，如果進一步細分單元將得到更精確的鋼束有效預應力分布。

［1］同濟大學橋梁工程系．大跨徑連續剛構橋箱梁抗裂性能研究［D］．上海:同濟大學，2005．

［2］李國平．預應力混凝土結構設計原理［M］．北京:人民交通出版社，2000．

［3］高 金．預應力對箱梁抗剪承載能力的影響分析［D］．上海:同濟大學碩士學位論文，2005．