基于小波濾波的激光陀螺SINS晃動基座初始對準

黃鳳榮，高 峰，付中澤，蔣茂榮，孫偉強

（天津航海儀器研究所，天津 300131）

基于小波濾波的激光陀螺SINS晃動基座初始對準

黃鳳榮，高 峰，付中澤，蔣茂榮，孫偉強

（天津航海儀器研究所，天津 300131）

激光陀螺捷聯慣導系統在晃動基座上進行初始對準時，由于激光陀螺信號中存在著很大的隨機噪聲，導致對準時間變長，對準精度降低。為解決此問題，提出一種基于小波實時閾值濾波的預處理方法，選取了合適的小波基和分解層數，對陀螺信號進行小波預處理，然后利用濾波后的陀螺信號進行姿態粗對準，最后使用速度誤差作為觀測量進行卡爾曼濾波精對準。半實物仿真試驗結果表明：本文提出的小波預處理方法在滿足陀螺信號實時性的條件下，能夠有效地減小激光陀螺信號中的各項隨機噪聲，利用預處理后的陀螺信號進行初始對準時，對準時間顯著縮短，航向角在精對準7 min左右收斂，其1σ值在 39″ 以內，在工程上有一定的參考價值。

小波預處理；捷聯慣導系統；初始對準；卡爾曼濾波

激光陀螺作為新一代的慣性測量元件，與傳統的機械陀螺相比，具有體積小、結構簡單、啟動快、精度高、數字脈沖輸出便于導航解算等許多優點，是目前最可靠、精度最高的陀螺之一。但在工程實際應用中，由于激光陀螺信號中存在著很大的隨機噪聲，這大大影響了激光陀螺捷聯慣性導航系統的初始對準的時間和精度。

對激光陀螺的隨機漂移補償方法通常有兩種：第一，針對慣性儀表輸出數據進行低通濾波[1-2]處理；第二，對激光陀螺隨機漂移進行時間序列建模[3-4]，依據模型設計卡爾曼濾波器，通過卡爾曼濾波進行補償。然而，低通濾波具有一定的局限性：濾波截止頻率過低將濾除有用信息，過高則難以有效濾除噪聲，對于有用信號與噪聲信號頻譜混疊的狀態，低通濾波更是無能為力。另外，由于激光陀螺信號受許多因素的干擾，難以獲得準確的漂移模型，無法得到理想的補償效果。

小波濾波[5-6]因其具有時頻特性和多尺度分析特性，特別適合于信號的分析與處理，具有很好的去噪效果。本文針對車載激光陀螺捷聯慣導系統的陀螺輸出信號，設計了一種小波實時濾波算法，以提高捷聯慣性導航系統初始對準[7-9]快速性和精度。

1 激光陀螺信號分析

對車載激光陀螺捷聯慣導系統的陀螺信號進行數據采集，采樣頻率為400 Hz。圖1顯示的為其中10 min的各軸陀螺數據。

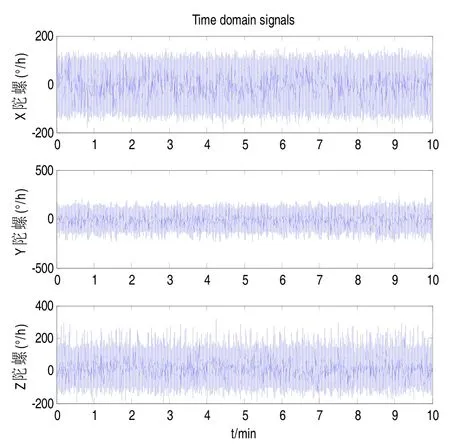
圖1 陀螺原始信號Fig.1 The original gyro signal

將上述陀螺原始信號記為θ(n)，其均值記為θ( 0)，由于陀螺有用信號頻率較低，可將θ(0)視為陀螺信號的理想輸出，則減去均值后的陀螺輸出表示為：

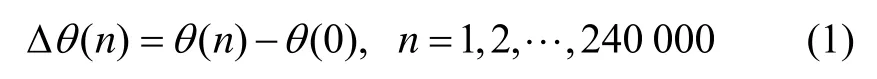
式中，θ(n)表示陀螺的實際輸出，Δθ(n)表示陀螺的輸出誤差。

圖2所示為陀螺信號輸出誤差的頻譜。從圖2中可以看出，陀螺誤差信號中含有較多的高頻噪聲，因此利用小波預處理陀螺信號的目的就是消除這些干擾，獲得陀螺輸出信號的低頻信息。

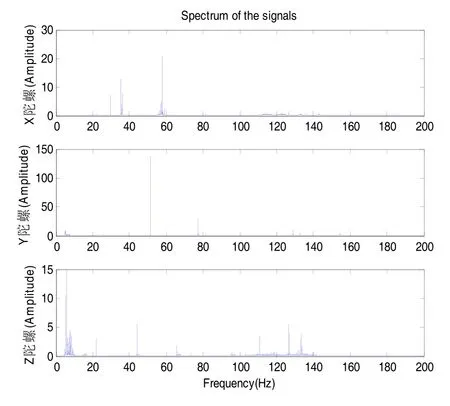
圖2 陀螺誤差信號的頻譜Fig.2 Frequency spectrum of the gyro error signal

2 小波實時濾波算法設計

2.1 小波去噪

小波閾值去噪是一種較為理想的濾波方法，不僅能夠有效地去除信號中的噪聲成分，而且能夠較好地保留真實信號。具體步驟如下：

① 小波基的選取

為兼顧濾波的去噪效果和實時性，選取的小波基主要應滿足：1）較短的支撐，以減小運算時間；2）對稱性，以避免信號失真；3）正交性，以便于用Mallat快速算法；4）較高的消失矩，以更好地匹配待分析的信號。綜合以上因素，db4小波是較好的選擇。

② 分解尺度和閾值函數的選取

針對一維信號，采用小波閾值濾波時，閾值的選取非常關鍵。由于通用的閾值確定方法都有一個前提條件，即小波分解后，有用信息集中在幅值較大但少數幾個小波系數中，而噪聲則處于小幅值但大多數的小波系數中。顯然這個前提條件在本文中得不到滿足。故采取強制去噪方法，該方法把小波分解結構中的高頻系數全部置為零，然后再對信號進行重構處理，該方法比較簡單，且重構后的信號也比較光滑，雖然可能丟失信號的有用成分，但是只要合理地選擇小波分解的尺度，分解的尺度只要不太大，信號的有用成分還是完全可以保留下來。因此，選取最大分解尺度為5。

2.2 實時濾波算法的設計

為滿足對激光陀螺輸出信號的實時處理，采用基于滑動數據窗的小波濾波算法，處理邊界問題時采用邊界值重復的對稱周期延拓方法；設數據窗的寬度為N，對于測試前的N-1個數據并不處理，待測量數據個數為N時，對這N個數據進行一次小波消噪處理，然后將濾波后的第N個數據作為濾波輸出，隨著數據窗的移動，就實現了信號的實時濾波。實時濾波算法如下:

①T時刻激光陀螺輸出信號為x(i)：

當T＜N時，

由于數據量較少不進行濾波，只完成濾波器的賦初值，a(i)為濾波器輸入序列。

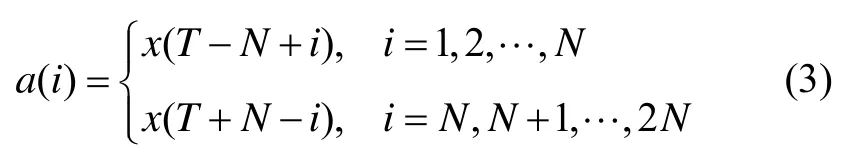
即完成了對輸入信號對稱周期延拓。

② 對a(i)進行Mallat多尺度分解和重構，則濾波后的信號可以表示為：

③ 濾波后輸出信號值：

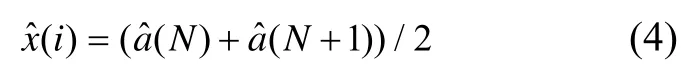
即完成一次單點實時濾波。讀入下一個激光陀螺輸出值x(i+1)，返回到步驟①，進行下一次濾波。

3 初始對準半實物仿真實驗

3.1 初始對準Kalman濾波器設計

本文選取當地地理坐標系(東北天)作為導航坐標系。當地地理坐標系下捷聯慣性導航系統的誤差模型為：

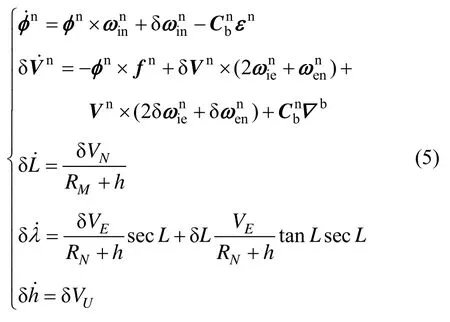
根據系統的誤差模型，選取姿態角誤差、速度誤差、位置誤差、陀螺常值漂移、加速度計零偏來構成狀態變量X：

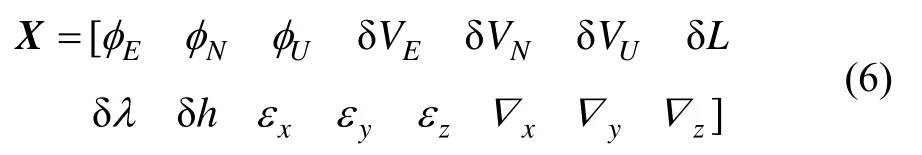
選取系統的外觀測量Z為速度誤差，即:

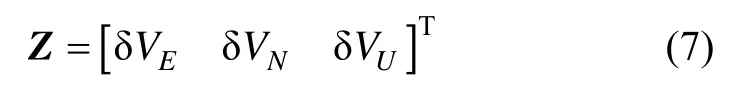
因此，系統的狀態方程和量測方程如下：

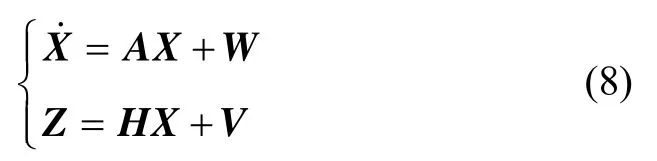
式中，A為系統狀態矩陣，W為系統噪聲，H為量測矩陣，V為量測噪聲。

3.2 晃動基座上初始對準半實物仿真

針對車載激光陀螺捷聯慣導系統采集的陀螺輸出信號，按上述所設計的小波濾波方法進行預處理，然后進行1 min粗對準，以確定初始姿態矩陣；待粗對準完成后，再根據上文設計的卡爾曼濾波器進行20 min 精對準。圖3為濾波后的各軸陀螺信號，從圖中可以看出，各軸陀螺信號噪聲得到了有效抑制。

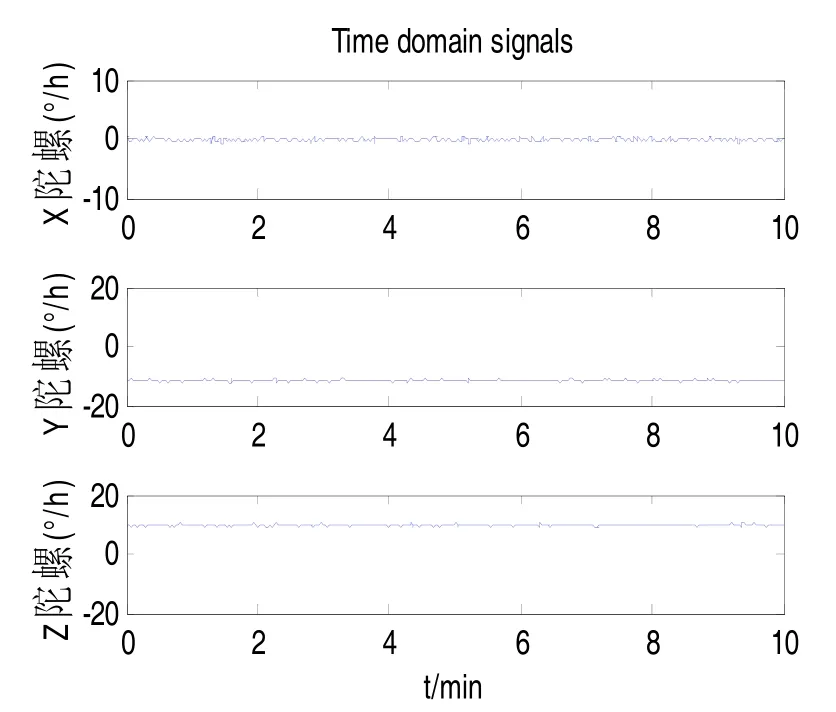
圖3 濾波后的陀螺信號Fig.3 The gyro signal after filtering

圖4所示為卡爾曼濾波精對準的半實物仿真試驗結果圖。初始對準半實物仿真試驗結果表明：小波預處理前航向角在精對準20 min內沒有收斂，而小波預處理后航向角的收斂速度明顯加快，在精對準7 min左右收斂。

為驗證小波實時濾波算法的有效性，針對該系統采集8組陀螺數據，每組數據時間為30 min，利用每組數據分別進行小波實時濾波、粗對準和卡爾曼濾波精對準。表1為經預處理后精對準7 min時的航向角，其1σ值為0.0109°，約為39″。因此，本文采取的小波預處理方法能夠有效地減小了陀螺信號中的隨機噪聲，有效地改善了航向角的對準精度，顯著縮短了對準時間。

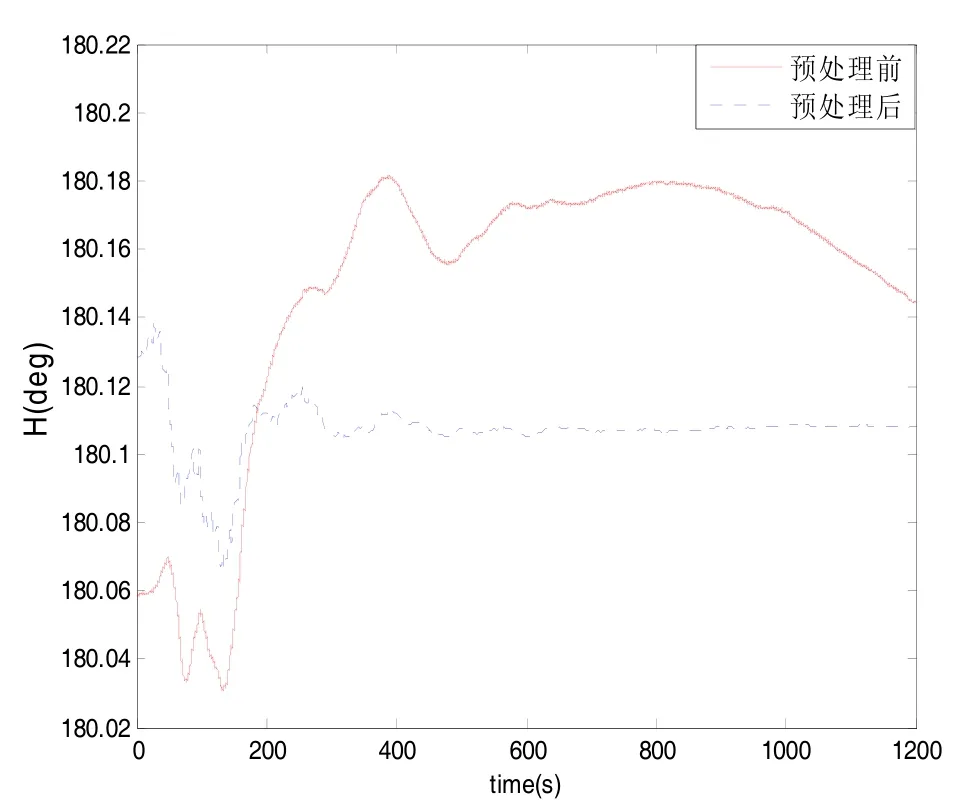
圖4 預處理前后初始對準試驗對比Fig.4 Comparison of initial alignment tests before and after preprocessing

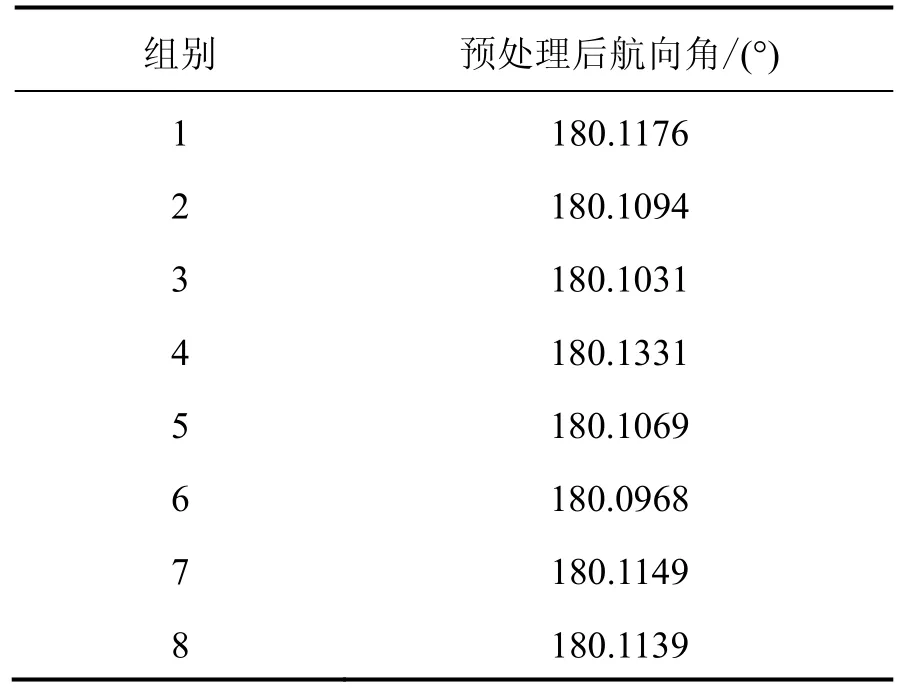
表1 預處理后的各組航向角Tab.1 The heading of each group after preprocessing

4 結 論

本文針對激光陀螺隨機噪聲影響捷聯慣性導航系統初始對準時間和精度的問題，設計出一種針對實測激光陀螺信號的小波實時預處理方法，進行了粗對準和卡爾曼濾波精對準半實物仿真試驗。

試驗結果表明：本文設計的小波預處理方法在滿足實時性的條件下，能夠有效地抑制陀螺信號中的各項隨機噪聲，預處理前航向角在20 min內無法完成對準，預處理后航向角在精對準7 min左右收斂，其1σ值約為 39″，故對準時間顯著縮短，對準精度得到有效改善，具有一定的工程應用價值。

[1]Chen Ansheng,Li Jianli,Chu Zhongyi.Dither signal removal of ring laser gyro POS based on combined digital filter[C]//Processing of 2012 8th IEEE Interna- tional Symposium on Instrumentation and Control Technology.Beijing,China,2012: 178-182.

[2]呂少麟，謝玲，陳家斌.晃動基座下激光陀螺捷聯慣導系統初始對準的預濾波[J].光學精密工程，2009，17(10)：2520-2527.Lü Shao-lin,XIE Ling,CHEN Jia-bin.Prefiltering for initial alignment of ring laser gyroscope SINS on rocking base[J].Optics and Precision Engineering,2009,17(10):2520-2527.

[3]Sun Feng,Luo Chao,Gao Wei,et al.Research on modeling and compensation method of fiber optic gyro’random error[C]//Proceedings of the IEEE International Conference on Mechatronics & Automation.Niagara Falls,Canada,2005: 461-465.

[4]Wang Ting,Gao Yanbin,Ma Tao.Research on FOG random errors modeling based on AFSA[C]//2012 International Conference on Industrial Control and Electronics Engineering.2012: 1243-1246.

[5]Xue Haijian,Guo Xiaosong.Gyro signal de-nosing based on a new wavelet threshold function[C]//2012 International Conference on Computer Science and Service System.Taiyuan,China,2012: 270-274.

[6]Llyas M,Yang Yunchun,Zhang Ren.SINS initial alignment using wavelet de-noising method for aircraft navigation[C]//Proceedings of the 10th World Congression on Intelligent Control and Automation.Beijing,China,2012:3921-3926.

[7]嚴恭敏.捷聯慣導系統動基座初始對準及其其它相關問題研究[D]. 西安： 西北工業大學，2008.YAN Gong-min.On SINS in-movement initial alignment and some other problems[D].Xi’an,China: Northwestern Polytechnic University,2008.

[8]翁海娜，姚琪，胡小毛.艦船單軸旋轉激光捷聯慣導系統動態初始對準[J].中國慣性技術學報，2012，20(1)：34-38.WENG Hai-na,Yao Qi,HU Xiao-mao.Dynamic initial alignment for single-axis rotation laser gyro SINS on board ship[J].Journal of Chinese Inertial Technology,2012,20(1): 34-38.

[9]Gao Fuquan,Ding Chuanhong.Initial alignment of strapdown inertial navigation system using Kalman filter[C]//International Conference on Computer Application and System Modeling.2010: 629-633.

Wavelet used in initial alignment of SINS on a rocking base

HUANG Feng-rong,GAO Feng,FU Zhong-ze,JIANG Mao-rong,SUN Wei-qiang
(Tianjin Navigation Instrument Research Institute,Tianjin 300131,China)

In initial alignment of RLG SINS on a stationary base,there are a lot of random noises in the RLG signals which may increase the alignment time and reduce the alignment precision.To solve this problem,a preprocessing method based on wavelet real-time threshold filtering is presented.The basic-wavelet and the proper level of wavelet decomposition are chosen.The gyro signal is preprocessed by using the wavelet.Then the coarse alignment is performed by using the filtered gyro signals.At last,velocity error matching and Kalman filtering are used to improve the precision of initial alignment.Experiment results show that the proposed wavelet preprocessing method can effectively reduce the RLG drift and satisfy the real-time demand.By using the preprocessed gyro signal,the initial alignment time is significantly reduced and the azimuth convergence can be accomplished in 7 min and the value of 1σ is within 39″,which could provide some references in engineering application.

wavelet preprocessing; SINS; initial alignment; Kalman filtering

U666.1

：A

1005-6734(2014)02-0157-04

10.13695/j.cnki.12-1222/o3.2014.02.003

2013-11-20；

：2014-01-26

國防重點預研項目(51309030201)

黃鳳榮(1969—)，女，工學博士，高級工程師，碩士生導師，主要從事導航、制導與控制系統研究。Email：2930183880@qq.com