時間延遲對姿態角匹配傳遞對準的影響

陳 剛，周 超，劉紅光

（天津航海儀器研究所，天津 300131）

時間延遲對姿態角匹配傳遞對準的影響

陳 剛，周 超，劉紅光

（天津航海儀器研究所，天津 300131）

姿態角匹配傳遞對準要求匹配信息在時間上統一。主子慣導之間存在傳輸延遲以及由于啟動時間點隨機性導致的解算點不匹配,造成信息在時間上不統一。分析了時間延遲對姿態角匹配傳遞對準的影響，并提出了一種將時間延遲分離并加以補償處理的方法。采用滯后子慣導信息的方式預先補償常值時延，而后采用狀態增強的方式估計補償隨機啟動時間點造成的隨機時延，從而達到匹配信息時間統一的要求。試驗結果表明，當主子慣導時間不同步，若不對時間延遲補償，姿態角估計誤差較大甚至不收斂；存在100 ms時間延遲時，相比于直接采用狀態增強的方式估計補償時間延遲，采用常值與隨機時延分別補償的方式卡爾曼濾波器收斂時間從28 s縮短至10 s，東向與北向水平估計精度分別提升至0.5′、0.3′，航向估計精度相同。

姿態角匹配；時間延遲；卡爾曼濾波；對準性能

現代戰爭要求武器具有更快的反應速度、更高的打擊精度以及動態打擊能力。其中反應速度取決于初始對準[1]時間，打擊精度取決于初始對準精度，而動態打擊又提出了動基座對準的要求。傳遞對準作為一種動基座初始對準技術得到了廣泛的研究，其利用已知的高精度的主慣導計算量或測量量作為信息源，通過傳遞對準的方式，來估計子慣導導航坐標系的失準角。

在傳遞對準實際應用中，由于主子慣導往往處于不同位置，使得其對準精度除了受主子慣導自身性能的影響外，還會受到桿臂效應、撓曲變形以及時間延遲等因素的影響[2-3]。其中桿臂效應和撓曲變形[4]分別影響子慣導敏感到的加速度和角速度值，直接影響到匹配量；而時間延遲則會造成匹配信息的時間上不統一，無法得到準確的對準匹配量。本文分析時間延遲的特點以及其對具有代表性的姿態角匹配傳遞對準的影響，和相應的補償措施。為方便討論，不考慮撓曲變形及桿臂效應的影響。

1 時間延遲的產生及其影響

1.1 時間延遲的產生

時間延遲從產生來源上講可以分為兩類：① 傳輸解算延遲：傳遞對準過程中主慣導信息傳遞至少要經過發送、傳輸及子慣導接收三個過程，該延遲為一常值加一個量級很小的白噪聲，一般而言這種白噪聲可以忽略。② 隨機啟動延遲：在實際的使用過程中，子慣導每次開機啟動在時間點上具有隨機性，將造成主子慣導解算時間點失配，引起時間延遲。以主子慣導的解算頻率均為50 Hz為例，由于隨機啟動可能會造成一個解算周期內，即0～20 ms的隨機時間延遲，該延遲值在[0,20]的區間內服從均勻分布。

綜合以上兩種因素可以得到時間延遲模型：

式中，τtran為常值傳輸解算延遲，τrandn為隨機啟動延遲。

1.2 時間延遲對姿態角匹配的影響及處理方法

理想狀況下卡爾曼濾波器要求狀態方程與量測方程處于同一時間點，對于姿態角匹配傳遞對準量測方程應有：

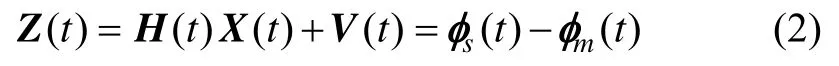
由于時間延遲τ的存在，在實際的傳遞對準過程中，子慣導在t時刻接收到的主慣導姿態角為。此時主子慣導匹配量時間點不統一，姿態角直接作差作為量測值進行傳遞對準誤差較大，需要進行時間點對齊處理。一般而言，匹配量時間點的對齊有兩種方法[5]：

1）外推匹配量：通過外推主慣導延遲匹配量的方式，得到子慣導當前時刻處主慣導匹配量的近似值，從而與子慣導匹配量作差得到量測值Z(t)，進行實時卡爾曼濾波。對于姿態角匹配即外推主慣導姿態角得到近似值。當時間延遲τ不大時，由泰勒展開并略去高階量得到線性化近似：

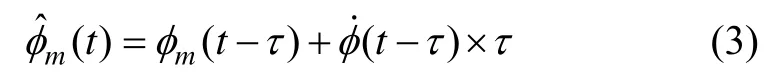
2）內插匹配量：通過滯后子慣導匹配量的方式，得到t-τ時刻處的子慣導匹配量，從而得到與主慣導匹配量時間統一的量測值，進行滯后卡爾曼濾波。對于姿態角匹配即需得到滯后的子慣導姿態角。一種思路是通過曲線擬合的方式獲取；也可以采用泰勒展開得到線性化近似。此時子慣導t時刻前的解算信息已知，可以選擇t-τ時刻后最近的解算點tk處的姿態角進行泰勒展開，有：

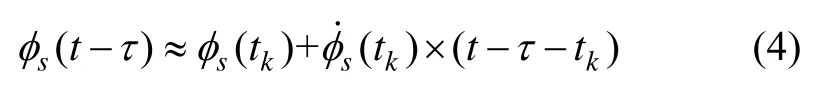
外推匹配量利用泰勒展開外推主慣導匹配量，得到t時刻線性化近似值。隨著時間延遲τ的增大，線性化近似的誤差將增大，影響對準量測值。內插匹配量也可以利用泰勒展開得到滯后的子慣導匹配量，其從t-τ時刻后最近的解算點進行內插，有效地將線性化近似時間限制在一個解算周期內，降低了誤差。但內插法在調整匹配量的同時還需將狀態轉移矩陣及量測矩陣統一至t-τ時刻才滿足整個濾波器處于統一的時間點，這無疑又增加了系統的計算量。

對于兩種時間對齊方式而言，都需要預先知道準確的時間延遲τ。由 1.1節的討論可知，傳輸解算延遲τtran近似為常值可以通過多種手段預先測量，但隨機啟動延遲τrandn是隨機變量無法預先測量，因此準確的時間延遲難以通過測量的方式預先得到。引入外部時間基準可以得到準確、實時的時間延遲[6]，但這種方法需要引入外部設備，同時也對主子慣導提出了更高的要求。而對于一些不具有統一外部時間基準條件的傳遞對準應用場合，可以通過狀態增強的方式將時間延遲τ作為濾波器狀態估計時間延遲。

姿態角匹配量在泰勒展開的同時在量測方程中引入了時間延遲使其可觀測，因此可將其作為狀態進行狀態擴充，在進行誤差估計的同時可以估計出時間延遲。

1.3 時間延遲的分別補償

針對不同時間延遲的特點，可以分別加以補償。由前面的討論可知時間延遲由傳輸解算延遲及隨機啟動延遲組成。傳輸解算延遲近似為常值且根據工程實際應用中的限制可能達到幾個解算周期的大小，而隨機啟動延遲為解算周期內的隨機值且滿足均勻分布。故可針對兩種延遲的特點分別進行補償，設解算周期為ts：

1）傳輸解算延遲：可以通過預先測量的手段得出其準確值，并利用內插匹配量的方式預先滯后子慣導匹配量進行補償。假定主子慣導進行n次隨機啟動外部測量得到每次的時間延遲，由于在解算周期內均勻分布，可得：

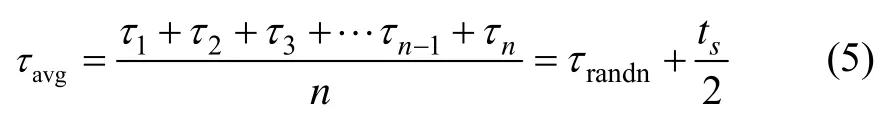
式中，τavg為時間延遲的平均值。令：

為常值。Δτ是時間點不匹配造成的延遲，且有。將子慣導匹配量滯后k個周期，此時的匹配量間的剩余時間延遲即為：

τ0在上服從均勻分布，即將時間延遲限制在2個解算周期之內。

2）隨機啟動延遲：具有隨機性，每次啟動均不同。可以采用狀態增強的方式將其與Δτ的和一起擴充為卡爾曼濾波器的狀態進行估計，即估計時間延遲τ0。而后采用外推匹配量的方式外推主慣導匹配量至t-τ+τ0處與內插滯后的子慣導匹配量處于同一時間點，記該點為T。此時，卡爾曼濾波器處于統一的時間點，可以進行標準卡爾曼濾波。

2 姿態角匹配傳遞對準模型及時間延遲的補償

2.1 狀態方程

捷聯慣導以東北天為導航坐標系。子慣導姿態誤差為φ，陀螺常值漂移為εb，主子慣導間安裝誤差角為μ。根據1.3節，采用分別補償的方式，預先滯后補償部分傳輸解算時間延遲，再將剩余延遲0τ作為待估計時間延遲，進行濾波器狀態擴充得到十維狀態向量。由捷聯慣導姿態誤差方程有：

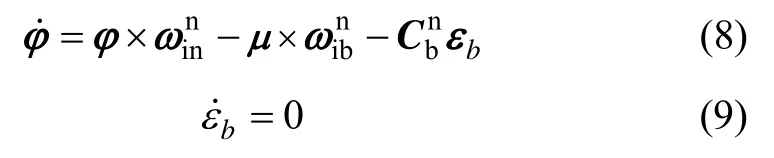
由于不考慮撓曲變形，認為μ為常值：

對于一次傳遞對準過程中，τ0不變：

經預先滯后補償將狀態方程統一至T時刻處。此時根據式(8)～(10)可得系統狀態方程：

式中，A(T)為狀態轉移矩陣，W(T)為系統噪聲。

2.2 量測方程

量測方程統一至T時刻處，將滯后的子慣導匹配量與主慣導匹配量作差得到量測值，并根據泰勒展開可得：

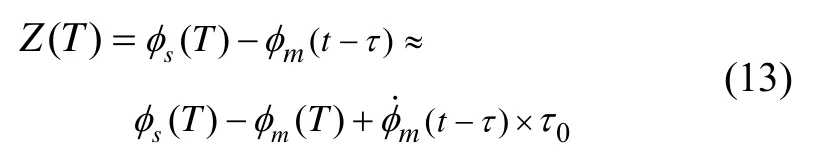
設主慣導和子慣導在T時刻處的姿態陣分別為，記：

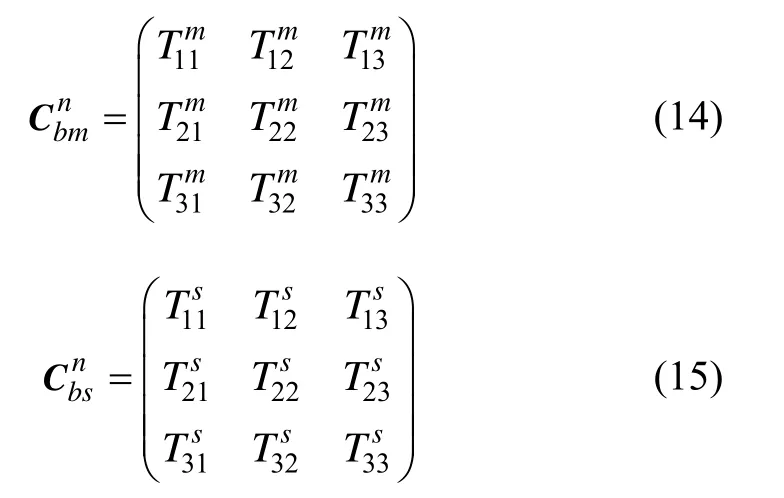
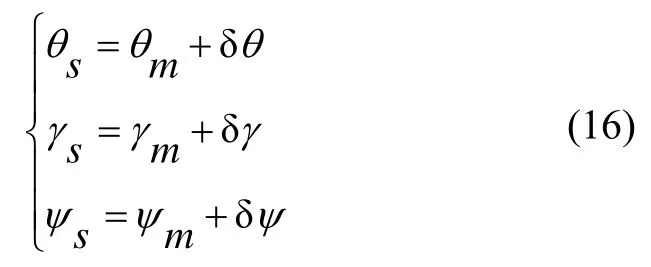
根據主子慣導姿態變換關系有：

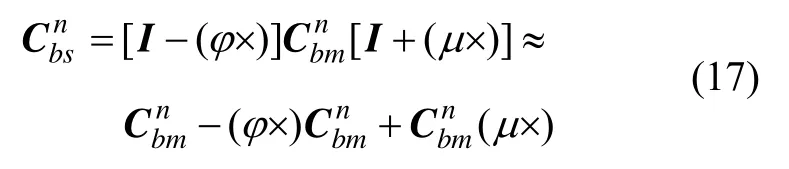
可以推導出：

3 試驗結果分析

3.1 試驗條件

初始位置為緯度30°，經度110°，高度0 m；初始姿態為 0；主慣導與子慣導間安裝誤差為[0.3°,0.4°,-1°]；主慣導陀螺常值漂移εx,εy,εz為[0.005°/h 0.005°/h 0.005°/h]；加表零偏▽x,▽y,▽z為[50 μg 50 μg 50 μg]；子慣導陀螺常值漂移εx,εy,εz為[0.01°/h 0.01°/h 0.01°/h]；加表零偏▽x,▽y,▽z為[100 μg 100 μg 100 μg]。

載體在海浪作用下做搖擺運動，搖擺規律如下：

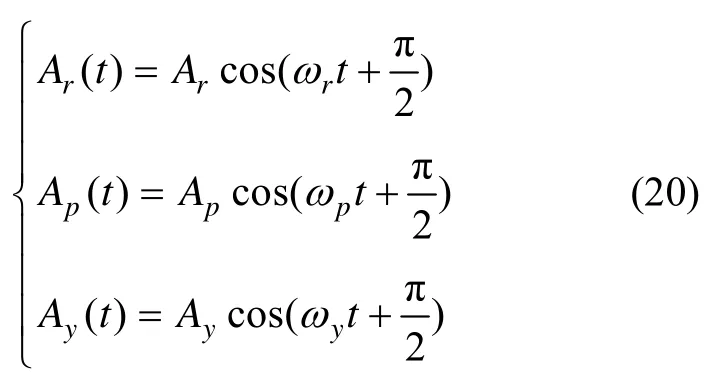
式中，Ar,Ap,Ap分別為橫滾、縱搖、艏搖幅值為8°、6°、4°，ωr,ωp,ωy為搖擺角速度分別以12 s、10 s、16 s為搖擺周期。

3.2 試驗結果分析

由式(8)～(11)(13)(18)(19)建立姿態角匹配傳遞對準卡爾曼濾波器，估計東北天姿態誤差角。忽略桿臂效應及撓曲變形的影響。

圖1表明，姿態角匹配傳遞對準方法估計姿態誤差角能夠快速收斂。當匹配量信息嚴格對齊時，即時間延遲為0 ms、100 s時，東向及北向估計誤差收斂到0.4′、0.3′，天向估計誤差收斂到1′，且在10 s處三個方向估計誤差即收斂到1′。

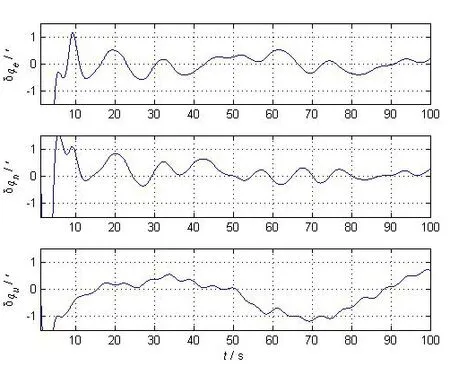
圖1 主子慣導無時間延遲姿態角估計誤差Fig.1 Estimation error of attitude angular deformations with no time delay

圖2表明，當存在100ms時間延遲時，濾波器在100s時仍處于大幅振蕩狀態。100s點處，東向估計誤差為3.5′，北向為4.5′，天向為29′。此時誤差過大，難以滿足子慣導對準使用要求。這說明對于姿態角匹配傳遞對準時間延遲的影響大，需要補償處理。

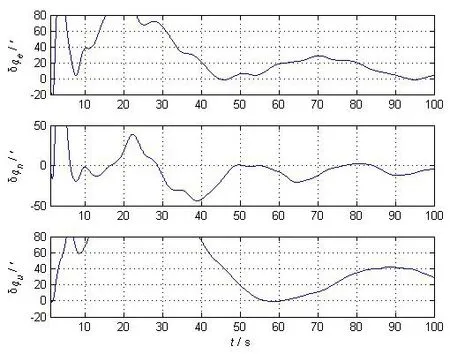
圖2 100 ms時間延遲姿態角估計誤差Fig.2 Estimation error of attitude angular deformations with 100 ms time delay

圖3表明，存在100 ms時間延遲，采用狀態增強的方式直接估計補償，估計出的姿態誤差角收斂。100 s時，東向及北向估計差收斂到 0.6′、0.4′，天向估計誤差收斂到1′。以1′為估計誤差收斂精度要求時，東向估計誤差在28 s處收斂到1′，北向估計誤差在23 s處收斂到1′，天向估計誤差在18 s處收斂到1′。

圖3 100 ms時間延遲采用狀態增強法補償姿態角估計誤差Fig.3 Estimation error of attitude angular deformations with 100 ms time delay after compensation

圖4表明，存在100 ms時間延遲，采用分別補償的方式補償時間延遲。對于100 ms時間延遲，假定待估計時間延遲為20 ms。預先滯后子慣導信息可補償80 ms時間延遲，后用狀態增強的方式對待估計時間延遲估計補償。估計出的姿態角收斂，100 s時，東向及北向估計誤差收斂到0.5′、0.3′，天向估計誤差收斂到1′，且在10 s處三個方向即收斂到1′。相比于無時間延遲估計結果，收斂時間與估計精度基本相同。

圖4 100 ms時間延遲采用分別補償姿態角估計誤差Fig.4 Estimation error of attitude angular deformations with 100 ms time delay after respective compensation

4 結 論

本文研究了姿態角匹配傳遞對準中時間延遲的影響。首先分析了產生時間延遲的原因及其特點，而后討論了其對姿態角匹配傳遞對準的影響并提出根據不同類型時間延遲的特點進行分別補償的方法。試驗結果表明當存在100 ms時間延遲時，采用直接狀態增強估計補償與分別補償的方法都能有效補償時間延遲帶來的影響且估計精度與無時間延遲相當。但分別補償法收斂速度更快，與無時間延遲情況相當，即與理想狀態下的濾波器的整體性能一致。

（References）：

[1]YAN Gong-min,WENG Jun,YANG Peng-xiang,QIN Yong-yuan.Study on SINS rapid gyrocompass initial alignment[C]//International Symposium on Inertial Technology and Navigation.2010-10: 323-330.

[2]劉紅光，陳剛，周超.角速度匹配傳遞對準方法在艦艇平臺的適用性分析[J].中國慣性技術學報，2013，21(5)：565-569.LIU Hong-guang,CHEN Gang,ZHOU Chao.Analysis of the angular velocity matching transfer alignment for vessel[J].Journal of Chinese Inertial Technology,2013,21(5): 565-569.

[3]Ravindran K，Bansal V.Delay compensation protocols for synchronization of multimedia data stream[J].IEEE Trans Knowledge and Data Engineering,1993,5(4): 574-589．

[4]Joon L,You-Chol L.Transfer alignment considering measurement time delay and ship body flexure[J].Journal of Mechanical Science and Technology,2009,23(1): 195- 203.

[5]徐林，李世玲，屈新芬.三種傳遞對準延時誤差補償方法的比較研究[J].兵工自動化，2011，2(2)：22-25.XU Lin,LI Shi-ling,QU Xin-fen.Comparison and study of three time-delay compensation methods for transfer alignment[J].Ordnance Industry Automation,2011,2(2):22-25.

[6]解春明，趙剡，楊傳春.信息時標不一致對傳遞對準的影響及修正[J].中國慣性技術學報，2010，18(4)：414-420.XIE Chun-ming,ZHAO Yan,YANG Chuan-chun.Influence and compensation of time-mark discrepancy in transfer alignment[J].Journal of Chinese Inertial Technology,2010,18(4): 414-420.

[7]劉紅光，陳志剛，陳剛.基準信息時間延遲對速度匹配傳遞對準性能的影響分析[J].中國慣性技術學報，2012，20(5)：544-551.LIU Hong-guang,CHEN Zhi-gang,CHEN gang.Timedelay’s effect on velocity matching transfer alignment[J].Journal of Chinese Inertial Technology,2012,20(5): 544-551.

[8]Abbas T,ZHANG Yun-yan,LI Yan-jun.SINS initial alignment for small tilt and large azimuth misalignment angles[C]//2011 IEEE 3rd International Conference on Communication Software and Networks.2011: 628-632.

[9]Sun Changyue,Deng Zhenglong.Transfer alignment of shipborne inertial-guided weapon system[J].Journal of Systems Engineering and Electronics,2009,20(2): 348-353.

Influence of time delay for attitude angle matching transfer alignment

CHEN Gang,ZHOU Chao,LIU Hong-guang
( Tianjin Navigation Instruments Research Institute,Tianjin 300131,China )

The attitude angle matching transfer alignment requires the matching information be uniform in time.Nevertheless there is a time delay between MINS and SINS because of the information transfers and the mismatch of calculating point.In this paper,the influence of the time delay for attitude angle matching transfer alignment is discussed,and a processing method for the time delay is proposed by respective compensation.It compensates the transmission time delay by delaying the SINS’s information,and compensates the random time delay by the time state enhancement method.The simulation results show that the estimation of the attitude angle error cannot be used if it doesn’t compensate the time delay.Compared with the time state enhancement method,the convergence time of Kalman filter will drop from 28 s to 10 s by using respective compensation method.The east and north level accuracies are superior to 0.5′ and 0.3′,respectively,and the heading accuracy isn’t changed.

attitude angle matching transfer alignment; time delay; Kalman filter; alignment performance

U666.1

：A

1005-6734(2014)02-0172-05

10.13695/j.cnki.12-1222/o3.2014.02.006

2013-12-20；

：2014-02-10

武器裝備預先研究項目（4010103010104）

陳剛（1973—），男，研究員，碩士生導師，研究方向為導航、制導與控制。Email：chen4023@eyou.com