基于球磨機的LS-SVM廣義逆內模控制研究
孫靈芳 李 丹
(東北電力大學自動化工程學院,吉林 吉林 132012)
球磨機制粉系統是火力發電廠里典型的多輸入多輸出系統,由于它具有非線性、強耦合特性,且至今難以實現多變量系統的穩定閉環控制[1]。因此,球磨機系統的自動控制問題仍是國內外學者研究的重點和難點。
針對球磨機系統的控制問題,常規的控制方法是PID(Proportional Integral Derivative)控制,其優點是控制模塊簡單,易于工程實現,但它的適應性差,難以跟蹤現場實時變化趨勢。隨著智能控制的飛速發展,將先進控制與常規控制相結合的復合控制方法為解決這類問題提供了一條新的途徑。如粒子群BP神經網絡PID優化算法[2]、模糊徑向基神經網絡PID算法[3]及專家模糊PID算法[4]等,這些算法復合了先進控制與常規控制兩者的優點,效果優于PID控制,但它們都以簡化球磨機模型為前提進行仿真分析,即球磨機是一個典型的三輸入三輸出系統,上述算法均先分解成一個雙輸入雙輸出被控對象和一個單變量被控對象,而簡化的模型與原模型存在的誤差問題未予考慮。若采用上述方法對球磨機三階模型進行控制仿真將導致系統穩定性變差,為解決這一問題,筆者采用LS-SVM廣義逆內模控制方法。由于LS-SVM可以在小樣本條件下精確辨識非線性系統[5],利用LS-SVM辨識球磨機的廣義逆系統,避免了模型誤差問題,與原系統串聯后構成開環控制的偽線性系統可以實現不完全解耦控制,最后引入內模可以提高閉環控制回路的魯棒穩定性。
1 LS-SVM廣義逆內模控制算法①
1.1 LS-SVM簡介
Suykens和Vandewalle提出的SVM(Support Vector Machine)算法,其基本思想是:通過非線性映射φ(x)把訓練樣本從低維空間映射到高維空間,在高維空間建立線性回歸函數。
給出訓練樣本集{(xi,yi),xi∈Rn,yi∈R},i=1,2,…,n,則LS-SVM的回歸線性輸出為:
y(x)=ωTφ(x)+b
(1)
式中b——偏置量;
ω——特征空間中具有相同維數的權向量;
φ(x)——非線性映射。
對式(1)進行函數預估,引入Lagrange函數,其中αi為Lagrange乘子,通過Karush-Kuhn-Tucker(KKT)條件簡化,從而得出LS-SVM的非線性回歸模型為:
(2)
1.2 廣義逆系統
逆系統是將非線性系統反饋線性化的一種常用方法,由逆系統發展起來的廣義逆系統與原系統串聯構成的偽線性系統,不但解決了原系統的耦合問題,而且通過合理地配置廣義逆系統參數使復合系統穩定,且易于實現。此外,廣義逆系統可以使高階系統不用降階而直接實現解耦控制,避免了模型因降階而導致的誤差問題,如圖1所示。
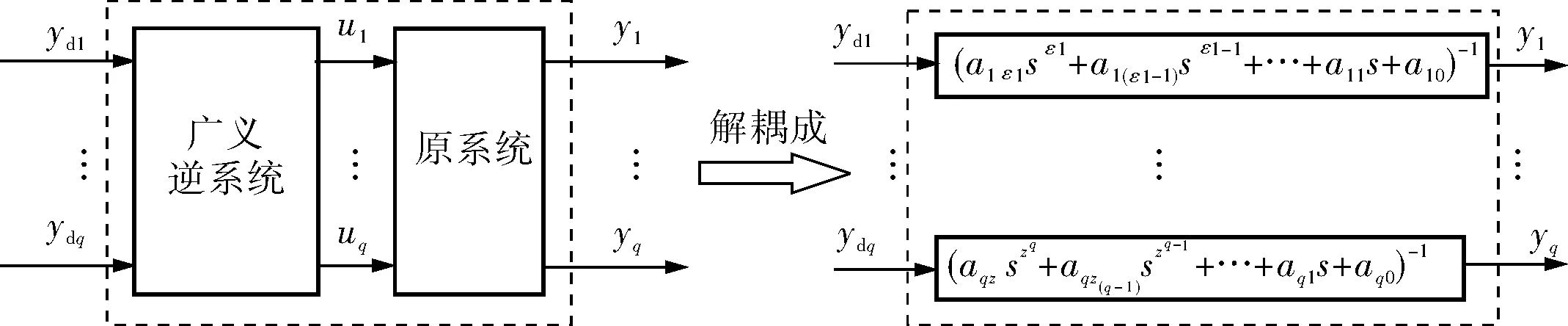
圖1 廣義逆系統的線性化與廣義逆偽線性復合系統
1.3 內模控制
由Garcia和Morari完整地提出并發展的內模控制(Internal Model Control,IMC),由于其具有結構簡單、參數整定直觀明了、魯棒性可在線調整及控制性能優越等優點,被廣泛應用到多輸入多輸出系統和非線性過程中,其原理圖如圖2所示。
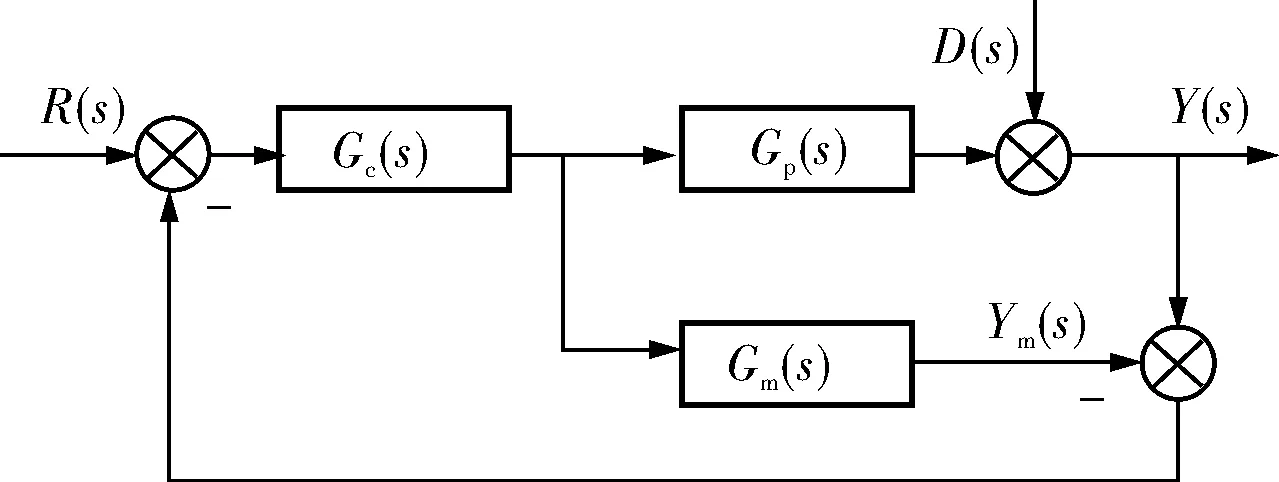
圖2 內模控制原理
2 LS-SVM廣義逆內模離散控制在球磨機系統上的應用
2.1 球磨機數學模型
筆者從機理法出發,以華潤某電廠單元機組配備的MGS4060型雙進雙出鋼球磨煤機為例建立相應的平衡方程[6],可得球磨機數學模型為:

(3)
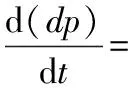
8438]·(273.15+tm)/273.15/134000}2
(4)
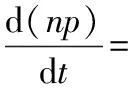
8438]·(273.15+tm)/273.15/134000}2
(5)
其中,tm、dp、np分別為球磨機出口溫度、進出口差壓和入口風壓;Bgm、Gr、Gl分別為給煤量、熱風量和冷風量。根據逆系統理論和Interactor算法,該模型的可逆性存在。
2.2 算法分析
根據球磨機的數學模型可知,該模型是一個典型的三輸入三輸出且帶有強耦合的非線性系統。筆者采用LS-SVM廣義逆系統與內模控制相結合的方法進行控制研究。
分析原系統的廣義逆系統,并與原系統串聯成偽線性復合系統。為了建立3個最簡的一階子系統,通過設置基本系數得到的偽線性系統如圖3所示。
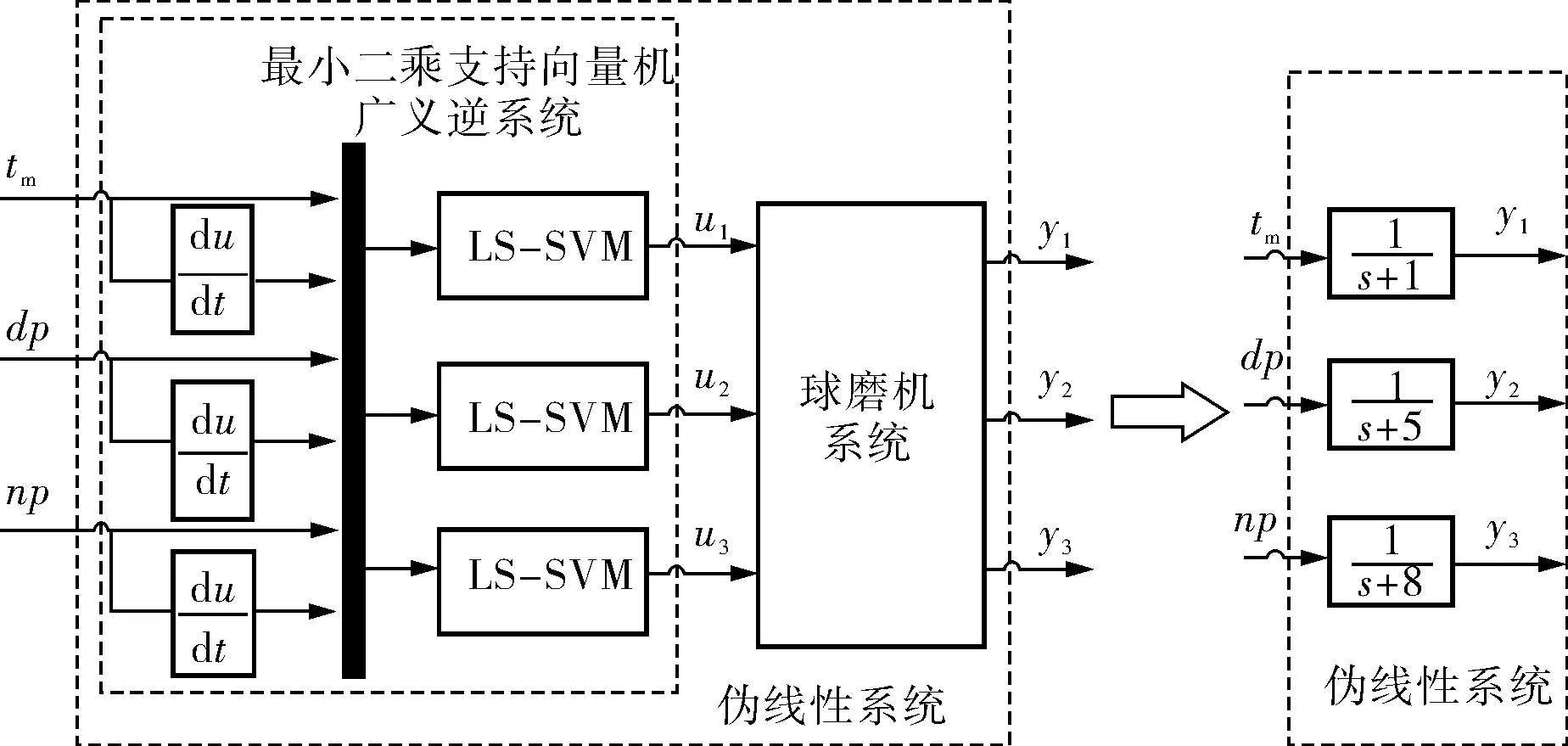
圖3 LS-SVM辨識的偽線性復合系統
用LS-SVM辨識廣義逆系統,具體步驟為:
b. LS-SVM參數確定。選RBF核函數為K(x,xi)exp{-‖x-xi‖2/2σ2},懲罰因子C和核函數參數σ。
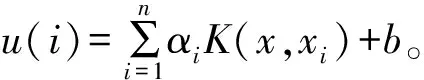
由于LS-SVM廣義逆系統是一個開環控制系統,許多不確定因素會導致系統輸出不穩定或控制性能變差,因此引入內模控制形成穩定的閉環控制系統,如圖4所示。
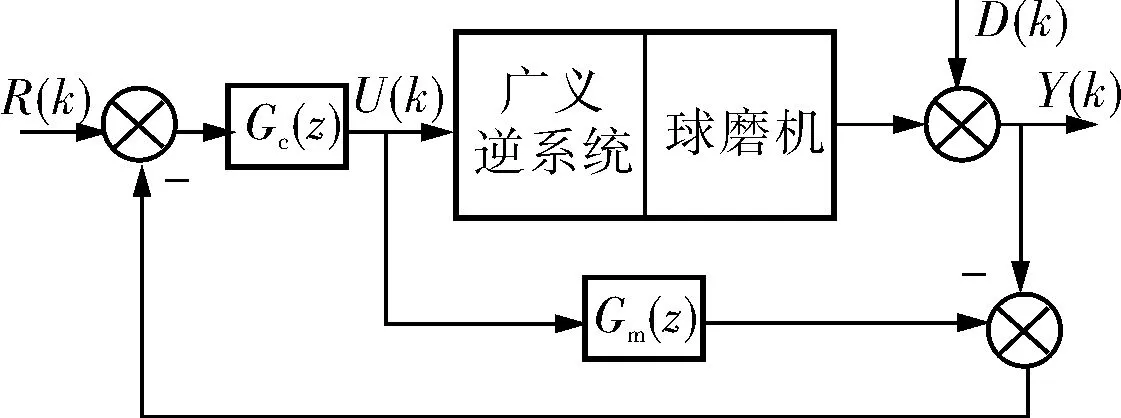
圖4 LS-SVM廣義逆內模控制框圖
圖4中,R(k)、U(k)、D(k)、Y(k)分別為輸入量、控制量、擾動量和輸出量;Gc(z)、Gm(z)分別為內模控制器和球磨機內模模型。為獲得更好的魯棒穩定性,設計濾波器F(z)=1/[1-exp(-λ)z-1],其中λ>0,因此得到控制器Gc(z)=F(z)·Gm(z)。
2.3 仿真研究
根據給定的訓練集和測試集,用LS-SVM進行廣義逆系統的模型辨識。當辨識出口溫度tm時,參數設置為:σ=140.1662,C=0.0645。獲得的α=0.0863,b=0.5651;當辨識球磨機進出口差壓時,參數設置為:σ=9.5256,C=0.0031。獲得的α=0.1521,b=0.492;當辨識球磨機入口風壓時,參數設置為:σ=113.7618,C=0.014。獲得的α=0.0736,b=0.4274。辨識效果如圖5所示。
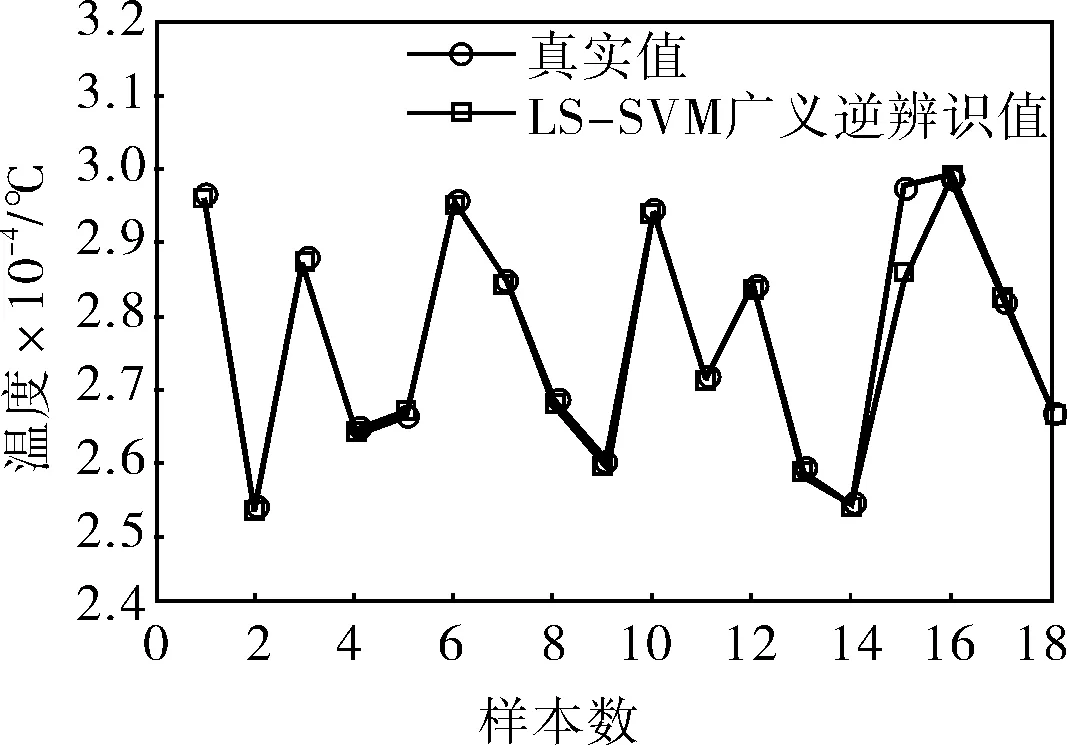
a. tm與真實值對比
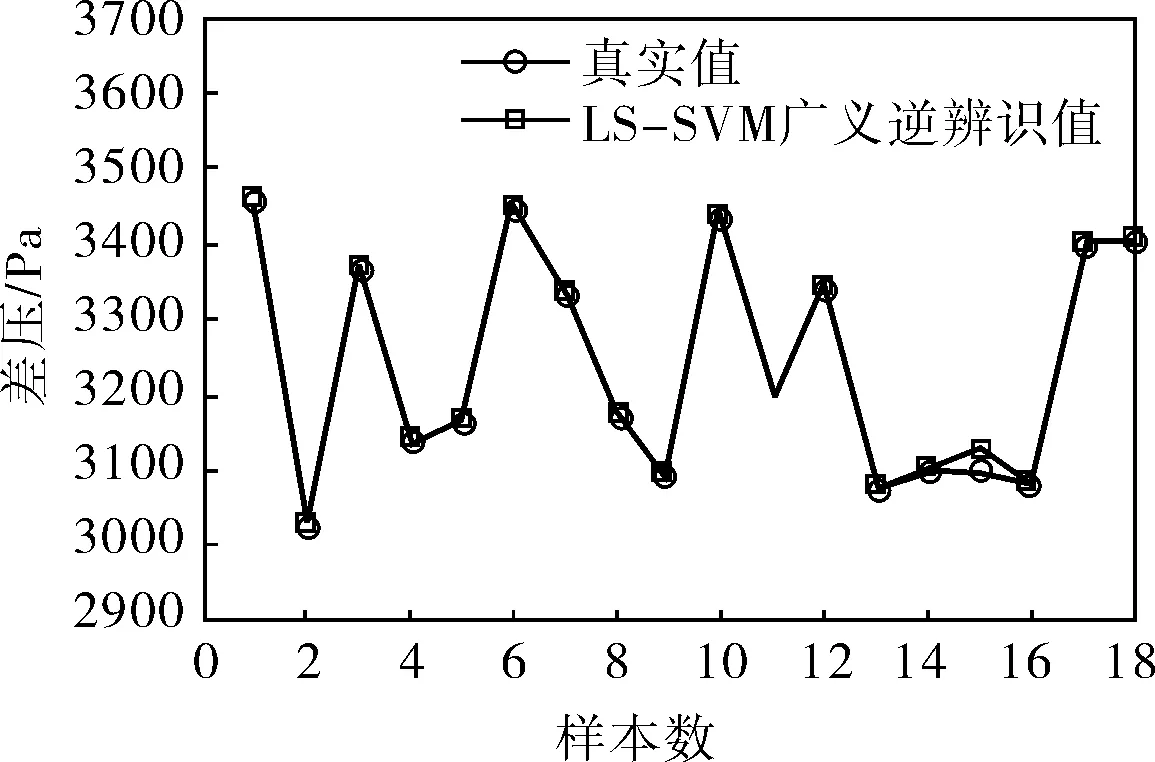
b. dp與真實值對比
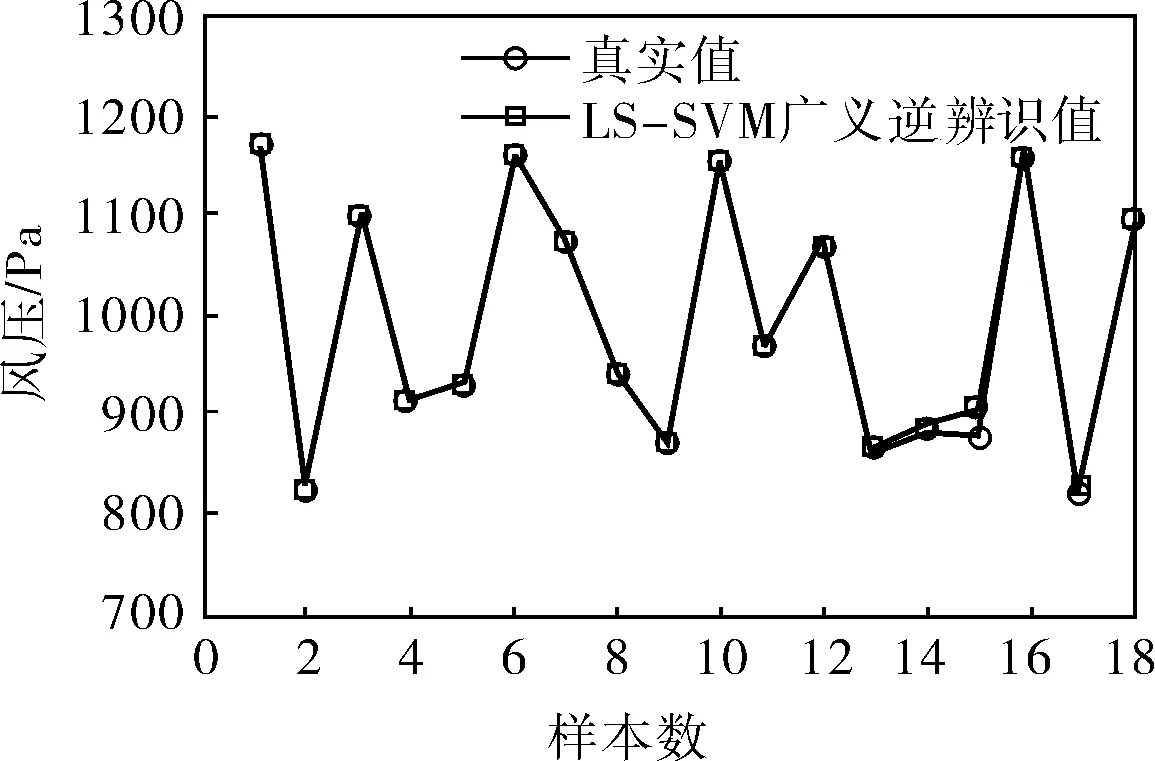
c. np與真實值對比
從圖5中可以看出,采用LS-SVM方法進行系統辨識具有較高的精度,可以真實反應球磨機的廣義逆系統,僅僅采用小樣本即可達到滿意的辨識效果。對其引入內模控制,使內模控制濾波器為F(z)=a/[1-exp(-b)z-1],其中a>0,b>0。對3個回路分別設置參數,具體參數值見表1,仿真圖如圖6所示。
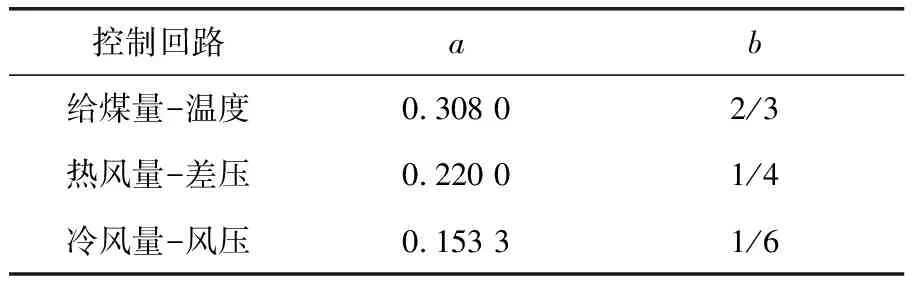
表1 內模控制濾波器參數值
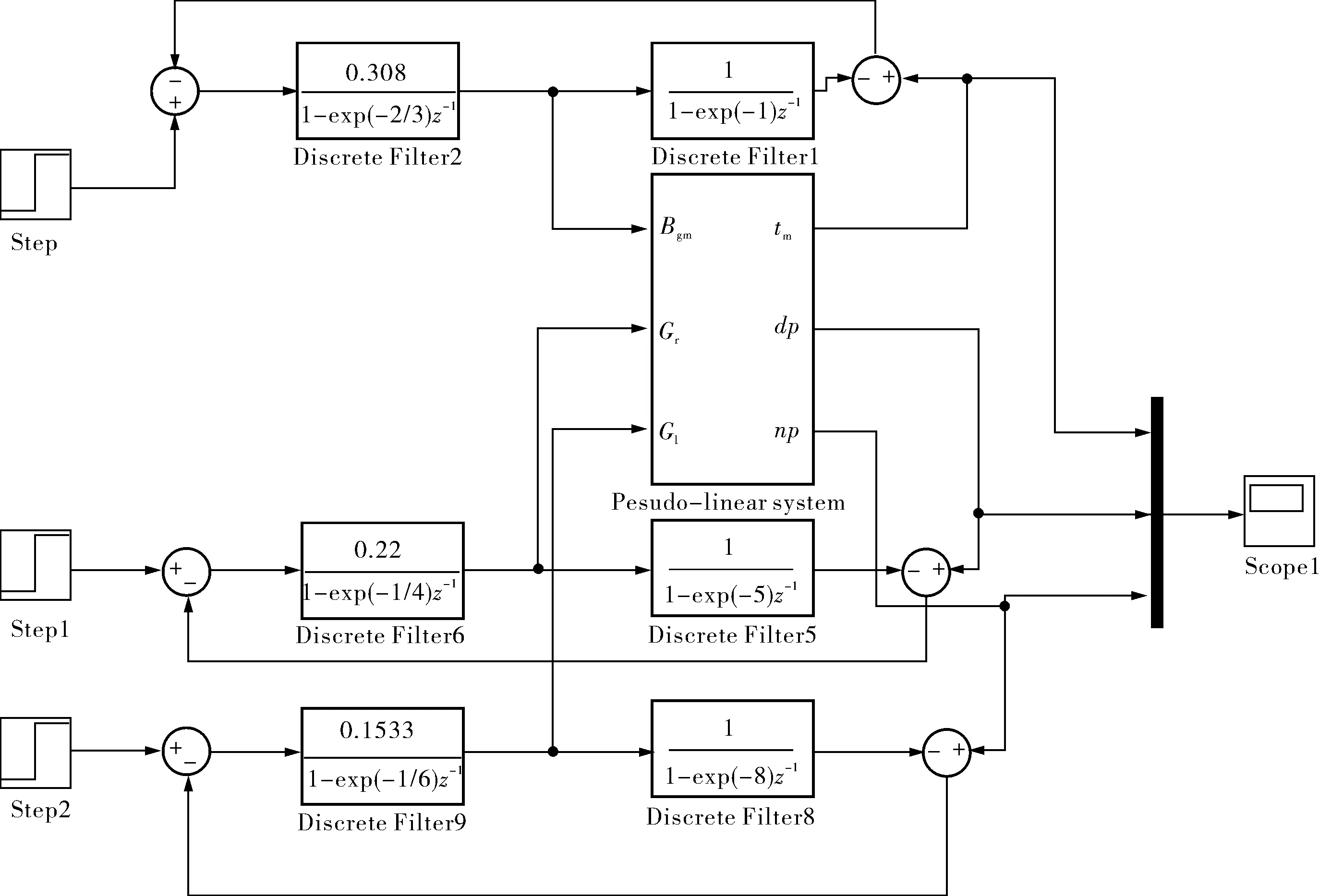
圖6 LS-SVM廣義逆內模控制仿真結構
筆者同時也給出了基于單回路的PID控制方法仿真對比,分別設置比例、積分和微分系數來使控制系統穩定,具體參數值見表2。采用圖6的控制結構對球磨機制粉系統的出口溫度tm、進出口差壓dp和入口風壓np分別進行控制,為使控制效果明顯,控制值分別設為1℃、1Pa和1Pa,仿真對比如圖7所示。
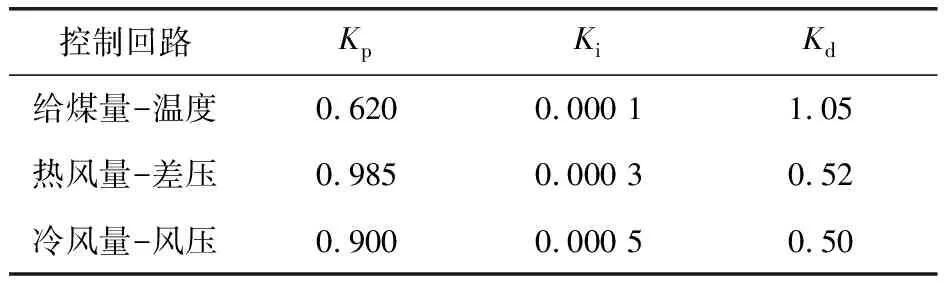
表2 基于單回路的PID控制系統參數值
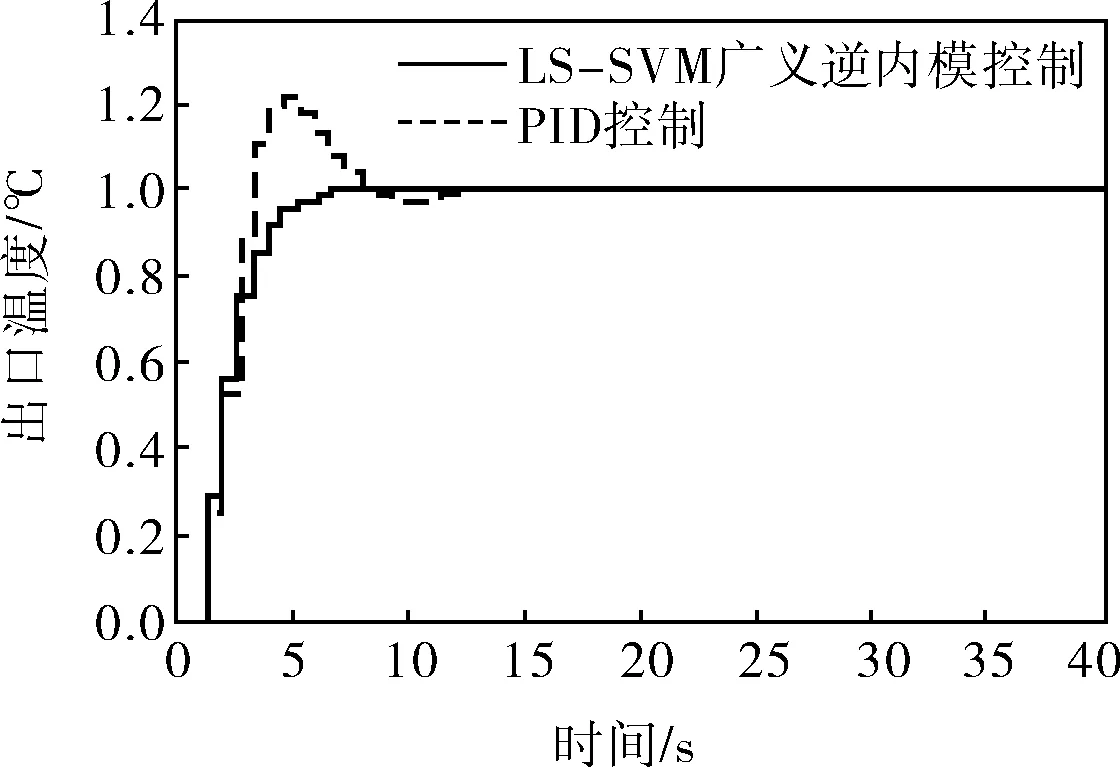
a. 對tm的輸出
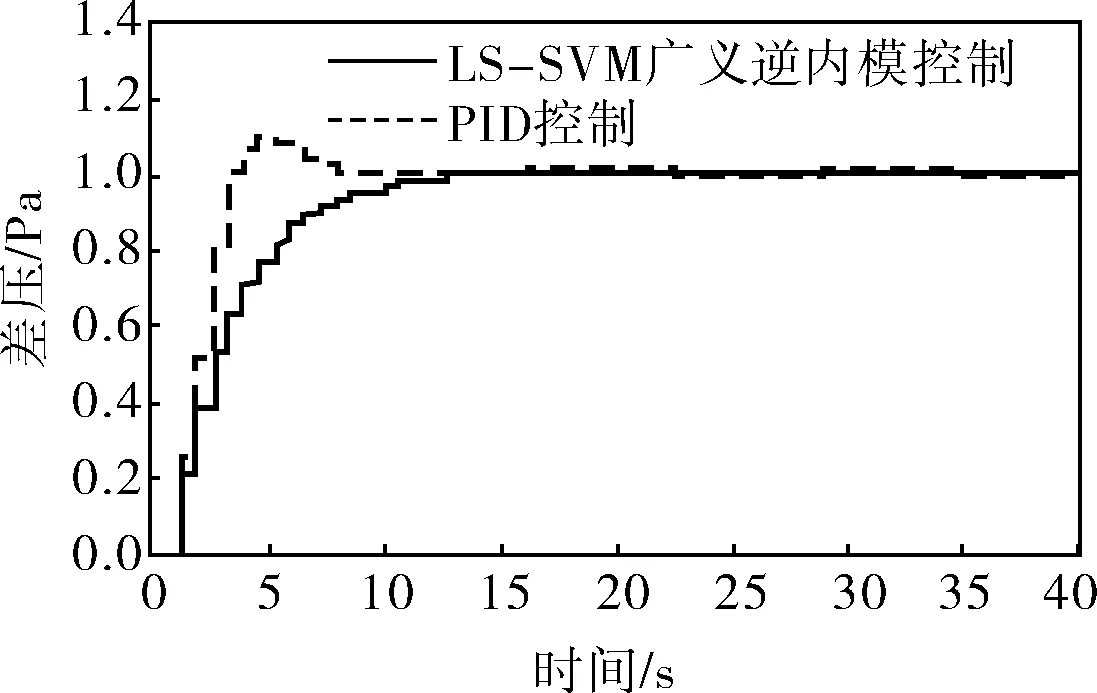
b. 對dp的輸出

c. 對np的輸出
從圖7中可以明顯看出,筆者采用的方法無超調,跟蹤平穩性、魯棒穩定性和準確性都優于常規PID控制方法,解耦控制效果明顯,很好地解決了高階復雜系統難以控制的問題,為多輸入多輸出系統的強耦合問題提供一種新的解決思路。
3 結束語
針對多變量、強耦合且難以建立精確數學模型的球磨機制粉系統,采用LS-SVM廣義逆內模控制方法進行控制研究。通過采用結構風險最小化的LS-SVM建立球磨機的廣義逆系統,不僅能準確逼近原系統的逆模型,而且結構簡單、支持小樣本訓練、泛化能力強;將廣義逆系統與原系統串聯可得到開環偽線性系統,實現了系統的不完全解耦與近似線性化,將偽線性系統前加入內模控制形成穩定的閉環回路,其動態響應與魯棒穩定性明顯增強。經仿真表明,所采用的復合控制算法較PID控制算法具有更好的穩定性且無超調,更好地實現了多變量之間的解耦控制,為解決高階復雜非線性系統的強耦合問題提供了一種可行的辦法。

