基于改進(jìn)型GPC算法的液位優(yōu)化控制

吳燕翔 高中勇

(上海海洋大學(xué)工程學(xué)院，上海 201306)

隨著化工行業(yè)的日益發(fā)展,化工生產(chǎn)的自動(dòng)化程度越來越高,要真正實(shí)現(xiàn)無人控制,化工自動(dòng)化是必不可少的環(huán)節(jié)[1]。在化工自動(dòng)化中，最常見的控制問題是液位控制。化工生產(chǎn)的實(shí)際液位控制問題都可以簡化為某種水箱的液位控制問題[2]。因此，液位是化工生產(chǎn)控制過程中一個(gè)重要的參數(shù)，特別是在動(dòng)態(tài)狀態(tài)下，采用合適的方法對(duì)液位進(jìn)行監(jiān)測、控制，能收到很好的操作效果[3]。

在化工生產(chǎn)中液位控制系統(tǒng)常用的是PID控制，經(jīng)典的PID控制適用于單輸入/單輸出系統(tǒng)，對(duì)多輸入/多輸出非線性系統(tǒng)的效果很難達(dá)到人們的預(yù)期目標(biāo)[4]。在這里，筆者引入廣義預(yù)測控制(GPC)。以雙容液位裝置為被控對(duì)象，基于NetCon平臺(tái)，利用MATLAB/Simulink程序開發(fā)工具，對(duì)廣義預(yù)測控制進(jìn)行仿真和實(shí)驗(yàn)研究。采用廣義預(yù)測控制算法，通過比較，選取改進(jìn)型GPC算法，即JGPC算法。通過仿真實(shí)例驗(yàn)證了這種算法在控制性能上的可行性和有效性。該算法提高了對(duì)非線性系統(tǒng)控制的穩(wěn)定性，克服了雙容水箱的容積延遲問題。

1 液位系統(tǒng)建模①

雙容水箱在化工工業(yè)過程控制中應(yīng)用非常廣泛。在雙容水箱水位的控制中,進(jìn)水首先進(jìn)入第一個(gè)水箱,然后通過第二個(gè)水箱流出,與一個(gè)水箱相比，由于增加了一個(gè)水箱，使得被控量的響應(yīng)在時(shí)間上落后一步,即存在容積延遲,從而導(dǎo)致該過程難以控制。

在控制系統(tǒng)的分析和設(shè)計(jì)中，首先要建立系統(tǒng)的數(shù)學(xué)模型[5]。控制系統(tǒng)的數(shù)學(xué)模型是定量描述系統(tǒng)或過程內(nèi)部物理量(或變量)之間關(guān)系的數(shù)學(xué)表達(dá)式[6]。利用辨識(shí)的方法建立系統(tǒng)的數(shù)學(xué)模型，首先根據(jù)系統(tǒng)辨識(shí)的目的，利用先驗(yàn)知識(shí)，初步確定模型結(jié)構(gòu)；然后采集輸入輸出數(shù)據(jù)并進(jìn)行相關(guān)處理，再進(jìn)行模型結(jié)構(gòu)辨識(shí)和模型參數(shù)辨識(shí)；最后經(jīng)過驗(yàn)證獲得最終模型。預(yù)測控制原理如圖1所示。

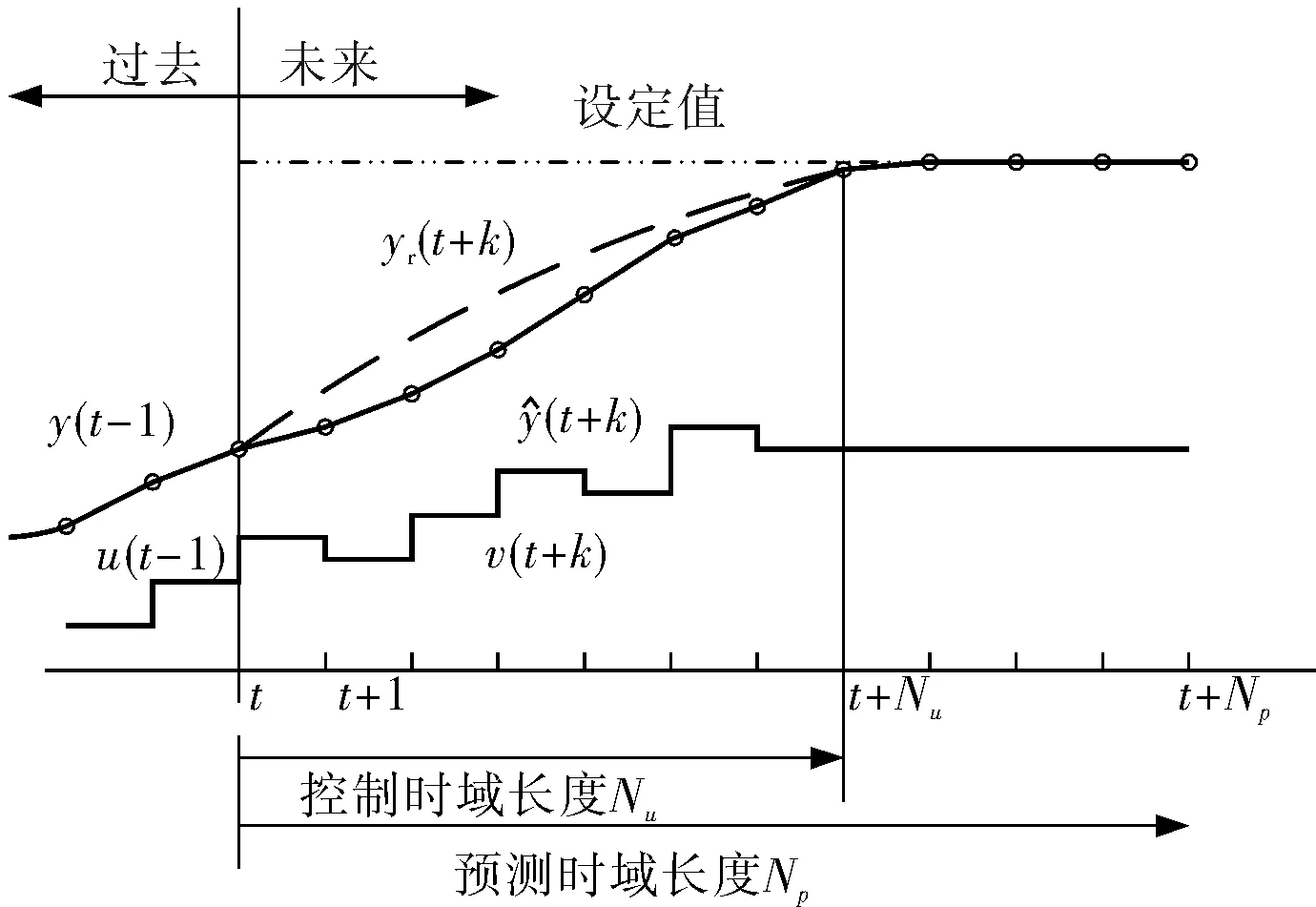
圖1 預(yù)測控制原理

2 GPC算法的優(yōu)化

2.1 GPC算法的比較

GPC算法中常用的是定常GPC算法、GPC自適應(yīng)算法和改進(jìn)后的GPC算法，即JGPC算法，這3種算法分別各有優(yōu)缺點(diǎn)，為了適應(yīng)所選系統(tǒng)，達(dá)到最好的控制效果，現(xiàn)進(jìn)行GPC算法的選取。設(shè)被控對(duì)象為如下開環(huán)不穩(wěn)定非最小相位系統(tǒng)：

y(k)-2y(k-1)+1.1y(k-2)=u(k-4)+2u(k-

5)+ε(k)/Δ

其中，ε(k)為方差為0.01的白噪聲。

3種算法的仿真如圖2～4所示。

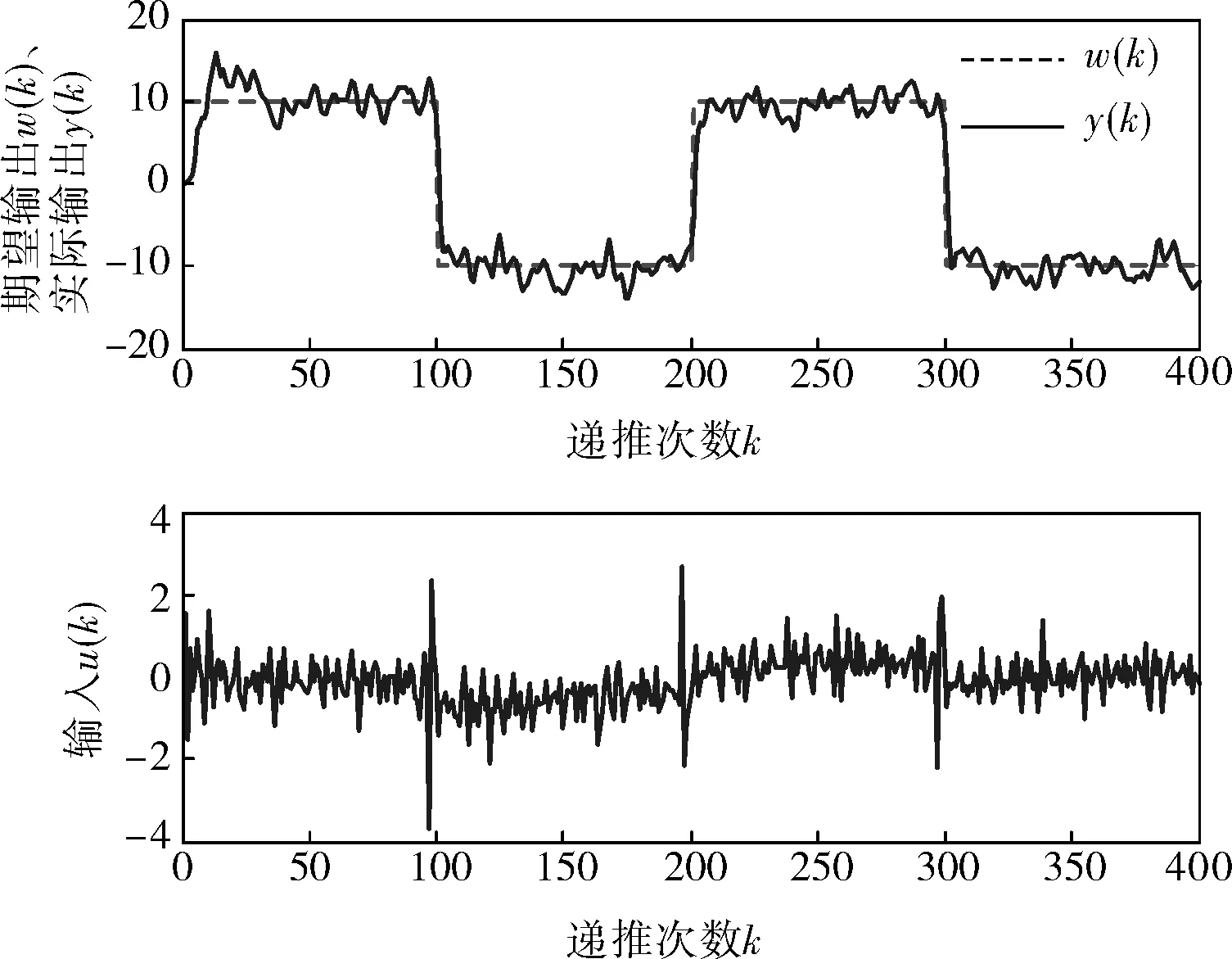
圖2 定常GPC算法仿真

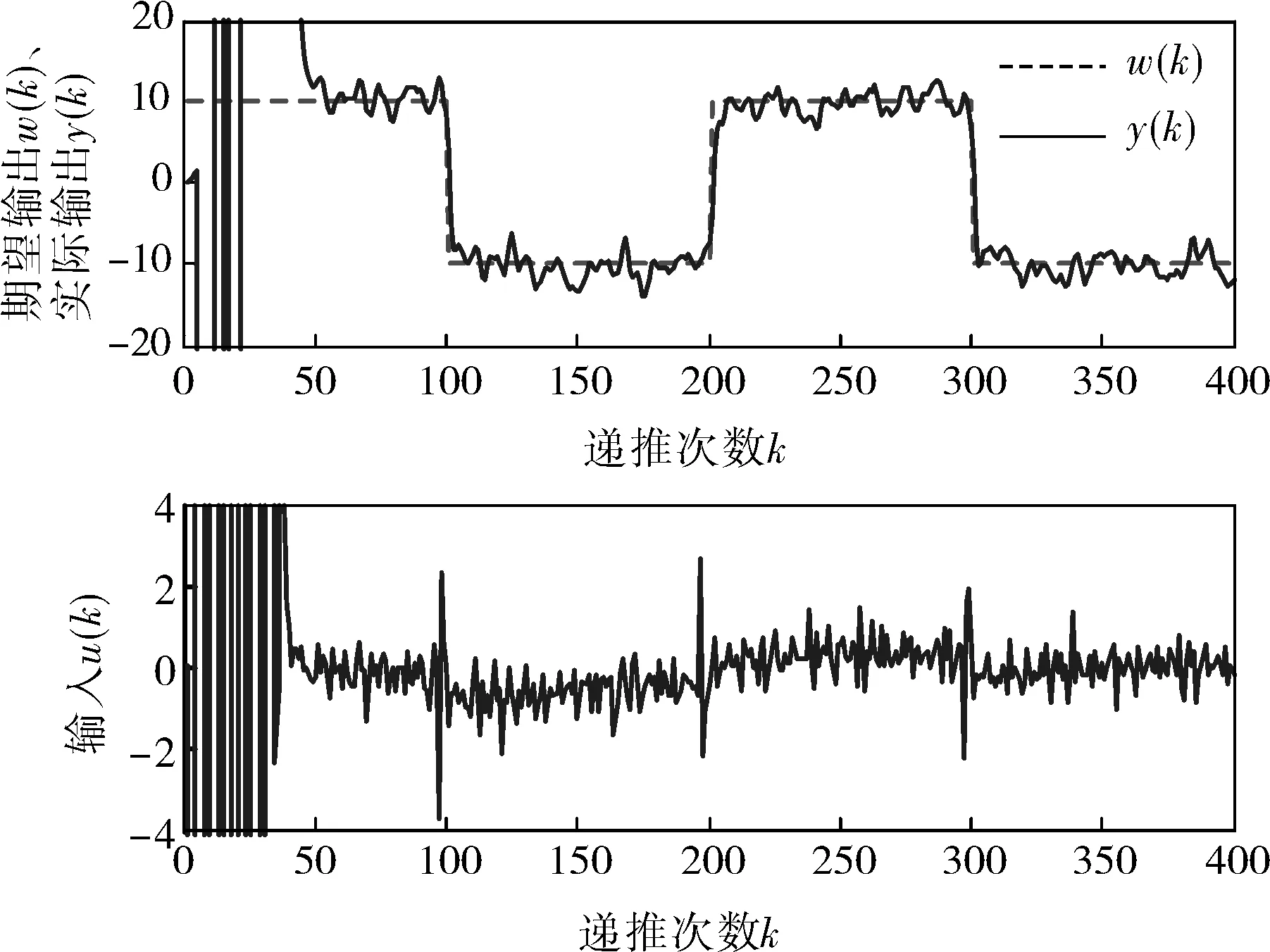
圖3 GPC自適應(yīng)算法仿真

圖4 JGPC算法仿真

通過對(duì)圖2～4的比較發(fā)現(xiàn)，GPC自適應(yīng)算法可以對(duì)未知的模型參數(shù)進(jìn)行辨識(shí)，對(duì)環(huán)境具有很好的自適應(yīng)性，當(dāng)系統(tǒng)模型參數(shù)被辨識(shí)出來后，控制信號(hào)u的變化不會(huì)那么劇烈，但是系統(tǒng)的調(diào)節(jié)時(shí)間可能會(huì)有所增加。該算法也有其固有的缺陷，如計(jì)算量較大及算法過于復(fù)雜等，且在實(shí)際應(yīng)用中還受到C(z-1)穩(wěn)定的限制。JGPC算法中，實(shí)際輸出值y(k)與期望輸出值w(k)更為接近，該算法適用于C(z-1)不穩(wěn)定的開環(huán)不穩(wěn)定非最小相位系統(tǒng)，所以在液位控制系統(tǒng)的實(shí)驗(yàn)中使用JGPC算法。

2.2 基于CARMA模型的JGPC算法

被控對(duì)象的CARMA模型可表示為：

A(z-1)y(k)=z-dB(z-1)u(k)+C(z-1)ε(k)

(1)

其中，y(k)、u(k)、ε(k)是系統(tǒng)的輸出、控制量和白噪聲；d為純延時(shí)。

由式(1)遞推，系統(tǒng)將來時(shí)刻的最小方差輸出預(yù)測模型為：

Y*=Ym+GΔU

(2)

Y*=[y*(k+d+1|k),…,y*(k+N|k)]T

(3)

Ym=[ym(k+d),ym(k+d+1),…,ym(k+N)]T

(4)

ΔU=[Δu(k),Δu(k+1),…,Δu(k+N-d)]T

(5)

(6)

式(4)中的ym(t+k)完全由過去的控制輸入和輸出確定。

極小化目標(biāo)函數(shù)：

J=E{(Y-Yr)T(Y-Yr)+ΔUTΓΔU}

(7)

得到相應(yīng)JGPC控制增量為：

ΔU=(GTG+Γ)-1GT(Yr-Ym)

(8)

則當(dāng)前時(shí)刻的控制量為：

u(k)=u(k-1)+Δu(k)

=u(k-1)+[1,0,…,0](GTG+Γ)-1GT(Yr-Ym)

(9)

3 液位控制系統(tǒng)的實(shí)驗(yàn)

3.1 參數(shù)整定

為知道各參數(shù)對(duì)液位系統(tǒng)模型的影響，不先對(duì)液位模型進(jìn)行系統(tǒng)辨識(shí)。利用MATLAB/Simulink程序開發(fā)工具對(duì)被控對(duì)象進(jìn)行仿真研究。預(yù)測長度N為15時(shí)y(k)的振蕩非常明顯，當(dāng)N逐漸增大時(shí)，振蕩減弱，仿真效果改善。當(dāng)預(yù)測長度取20時(shí)y(k)達(dá)到穩(wěn)定，仿真效果為最佳，故取N=20。對(duì)于遺忘因子λ，在仿真曲線中λ增大到2以后，振蕩變大，可得λ最優(yōu)取值為1。若取輸出柔化因子α=0.2，實(shí)際輸出曲線振蕩比較劇烈，隨著α的逐漸增加，實(shí)際輸出w(k)逐漸穩(wěn)定，但是當(dāng)α大于0.7時(shí)，實(shí)際輸出曲線與理想輸出曲線的契合度變差。所以，α=0.7為最佳。

綜上所述，JGPC算法的參數(shù)設(shè)定為預(yù)測長度N=20，遺忘因子λ=1，輸出柔化因子α=0.7。

3.2 液位系統(tǒng)的仿真實(shí)現(xiàn)

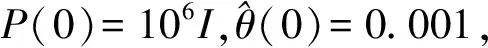
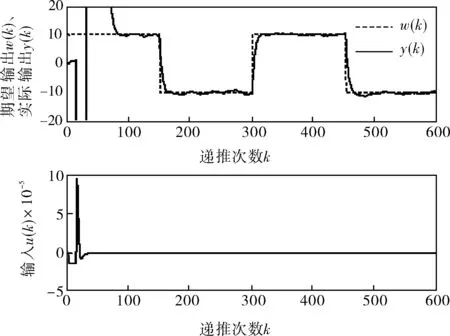
圖5 控制效果

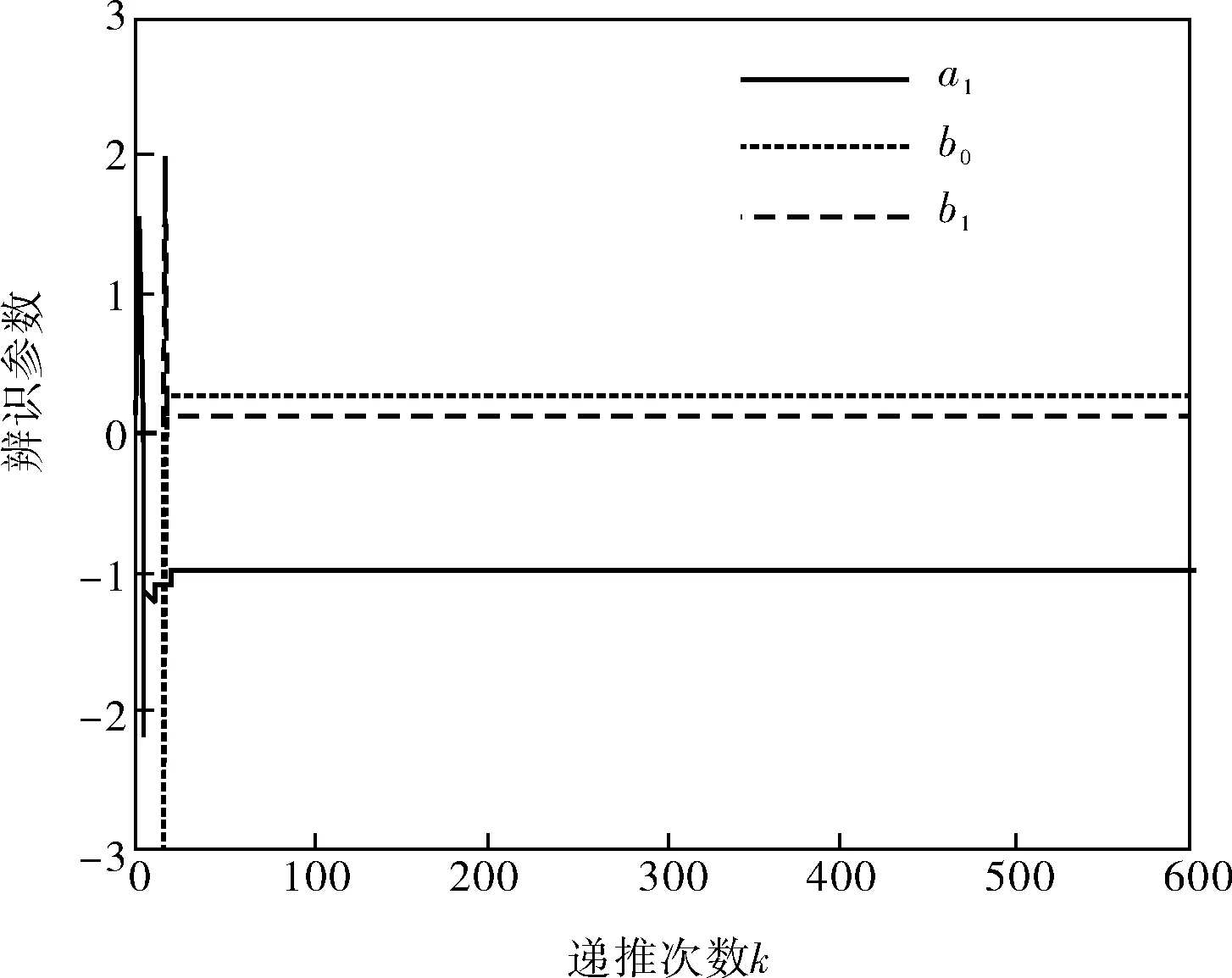
圖6 對(duì)象參數(shù)估計(jì)結(jié)果

通過對(duì)參數(shù)的整定，得到了較好的仿真結(jié)果，有效地控制了液位的穩(wěn)定。JGPC算法對(duì)液位的控制十分有效。

4 結(jié)束語

利用MATLAB/Simulink程序開發(fā)工具，對(duì)廣義預(yù)測控制進(jìn)行仿真和實(shí)驗(yàn)研究。引入廣義預(yù)測控制算法，通過分析比較選擇改進(jìn)后的JGPC算法。最后通過雙容水箱實(shí)際系統(tǒng)應(yīng)用，驗(yàn)證了這種算法在控制性能上的快速性和穩(wěn)定性，對(duì)將其運(yùn)用于化工生產(chǎn)液位控制系統(tǒng)具有借鑒意義。