一種全新的消除雙法蘭智能差壓變送器液位測量誤差的方法

劉子云

(中國神華煤制油化工有限公司北京工程分公司，北京 100011)

在化工生產及食品加工等行業，液位是重要的工藝參數之一。液位測量儀表種類繁多，如差壓式液位變送器、超聲波液位計、雷達液位計及浮筒液位計等，可依據工藝和設備的實際工況選用不同類型的液位測量儀表[1～3]，較常用的是浮筒液位計和差壓變送器。

利用傳統方法來計算液位差壓變送器的零點與量程，變送器的指示值與實際液位往往有較大誤差。筆者將通過分析誤差產生的原因，給出一種新的計算雙法蘭智能差壓變送器零點與量程的方法，使變送器的指示值與就地液位計的指示值在整個測量范圍內一致。并通過函數關系式和直角坐標圖說明，當測量液位的差壓變送器的輸出與實際液位存在誤差時，在某一測量點只調整變送器的零點或變送器的量程，使差壓變送器的輸出與實際液位相等的方法是無法滿足實際生產要求的，只有采取正確的方法同時調整差壓變送器的零點與量程，才能使變送器的輸出與實際液位在整個測量范圍內相一致。間接地消除了被測介質的密度對測量結果的影響，同時也間接地克服了雙法蘭液位差壓變送器的零點漂移問題。

1 影響液位差壓變送器輸出的主要因素①

液位差壓變送器的輸出可用下列關系式表達：

OUT=(Δp-Δp0)÷(Δp100-Δp0)×(20-4)+4

=16×(Δp-Δp0)÷(Δp100-Δp0)+4

(1)

式中OUT——輸出，4～20mA對應指示液位0%～100%；

Δp——正、負壓室間的壓差，kPa；

Δp0——零點，kPa；

Δp100——量程，kPa。

可以看出，當差壓變送器的零點與量程一定時，其輸出隨著Δp的變化而變化；在測量介質、安裝條件和運行條件一定的情況下，對于某一點的液位而言，Δp是一個定值，此時影響其輸出的主要因素是差壓變送器的零點(Δp0)與量程(Δp100)。

2 利用雙法蘭差壓變送器測量液位的研究

圖1為某煉油廠催化裂化裝置利用雙法蘭智能差壓變送器測量塔釜液位的安裝示意圖，T-301是穩定塔；用于測量穩定塔釜液位的LT-30301是EJA118W-EMSA2CA-AAAZ-97EB/NS/F1/C3型雙法蘭差壓變送器，其毛細管長度為12m，毛細管填充高溫硅油，硅油密度ρ2為1 070kg/m3，塔釜內的介質為穩定汽油，設計操作壓力1.25MPa，設計操作溫度184℃，設計給出的穩定汽油密度ρ1為505kg/m3，兩法蘭取源間距H為3.6m；變送器的安裝高度距正取壓法蘭間距(H1)為6m。LG30301為與T-301塔釜相連接的玻璃板就地液位計。

圖1 雙法蘭差壓變送器安裝示意圖

2.1 零點和量程的傳統計算

如圖1所示，當T-301塔釜內的穩定汽油液位為h時，由液柱壓強公式P=ρgH可得[4]：

Δp=p+-p-

=ρ1gh+ρ2gH1-(ρ2gH+ρ2gH1)

=ρ1gh-ρ2gH

(2)

式中g——重力加速度，9.80m/s2；

h——雙法蘭差壓變送器指示的T-301塔釜穩定汽油液位高度，0～3.60m；

H——雙法蘭差壓變送器正、負取壓法蘭間距(3.60m)；

H1——雙法蘭差壓變送器到正取壓法蘭間的高度(6.0m)；

p+——雙法蘭差壓變送器正壓室壓力，kPa；

p-——雙法蘭差壓變送器負壓室壓力，kPa；

ρ1——設計給定的T-301塔釜內穩定汽油的密度，505kg/m3；

ρ2——LT-30301雙法蘭差壓變送器毛細管內硅油密度，1 070kg/m3。

由式(2)可知，當h=0m時LT30301雙法蘭液位差壓變送器的零點Δp0=p+-p-=-ρ2gH=-1070×9.80×3.6÷1000≈-37.75kPa；當h=3.6m時，變送器的量程Δp100=p+-p-=ρ1gH-ρ2gH=(505×9.80×3.6-1070×9.80×3.6)÷1000≈-19.93kPa。

2.2 測量結果

按上述計算將雙法蘭差壓變送器的零點調至-37.75kPa，量程調至-19.93kPa。當裝置運行穩定(T-301塔釜壓力1.15MPa左右，溫度不詳)且將LT30301投入使用后，LT30301指示值(控制室內DCS指示值)與T-301塔釜實際汽油液位值(LG30301玻璃板液位計示值)存在較大誤差，詳見表1。

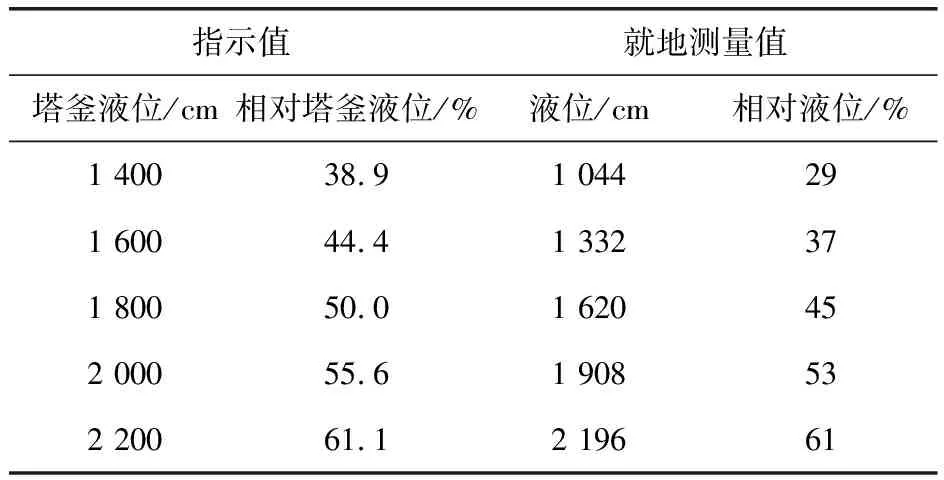
表1 T-301塔釜實際液位與儀表指示值

從表1中的數據可以看出：差壓變送器的輸出值與實際塔釜液位誤差較大；差壓變送器的輸出值高于實際塔釜液位；實際塔釜液位與差壓變送器的輸出值間的誤差不同，隨著液位的升高，誤差逐漸減小。

3 產生誤差的原因分析

從式(2)可以看出，當液位一定時，測量液位的差壓變送器的正、負壓室間的壓差是一個定值。從式(1)可以看出，變送器的輸出與實際液位間的誤差是由變送器的零點和量程不準確造成的，其原因是：

a. 利用式(2)計算液位差壓變送器的零點和量程時，T-301塔內的穩定汽油的設計密度ρ1與T-301塔內的穩定汽油實際密度不符。在實際生產過程中，T-301塔釜內汽油本身是一種混合物(由多種碳氫化合物組成)，且T-301實際操作壓力和溫度與設計給定的操作壓力和溫度有差異，因此T-301塔釜內汽油的實際密度ρ1是無法確定的。

b. 塔釜內穩定汽油的上部有油氣和其他烴類氣相物質，由于無法確定這些物質的密度，在用式(2)計算變送器的零點和量程時，給忽略了。

c. 從設計給定的數據來看，穩定塔的操作溫度為184℃，雙法蘭差壓變送器的正取壓法蘭與汽油液體接觸，而變送器的負取壓法蘭與塔釜內汽油液體上部的氣體接觸，由于差壓變送器的正、負法蘭所接觸的介質不同，因此變送器正、負法蘭膜片間產生了溫度差，使得變送器兩毛細管內的硅油膨脹不一致，這樣就會使變送器產生零點漂移[5]。由于很難準確得知變送器正、負法蘭膜片間的溫差，無法準確得知變送器的零點漂移量，因而在利用式(2)計算變送器的零點和量程時也無法考慮這些因素。

4 推導被測容器液位與測量液位的差壓變送器正、負壓室間的壓差關系式

由誤差產生原因，再結合式(2)可得：

Δp=p+-p-=ρ1gh-ρ2gH+ρ3g(H-h)+ΔZ

(3)

其中，ρ3為T-301內穩定汽油上部氣體的密度；ΔZ為差壓變送器產生的零點漂移，包括：因膜片接觸不同介質所產生的溫度差造成的零點漂移；由于環境溫度對毛細管內硅油的影響所引起的差壓變送器的零點漂移[5]；由于安裝引起的差壓變送器的零點漂移；其他原因引起的差壓變送器的零點漂移。

式(3)是計算差壓變送器零點和量程的準確關系式，但由于無法準確獲得：T-301塔釜內穩定汽油的密度ρ1；塔釜內穩定汽油液位的上部油氣和其他烴類的氣相物質的準確密度ρ3；差壓變送器所產生的零點漂移ΔZ。因此，無法按式(3)計算得到準確的零點和量程。

分析式(3)，當液位雙法蘭差壓變送器按設計要求安裝后，法蘭取源間距H可以用米尺準確測量，即H為定值；重力加速度g是常數；盡管在實際生產過程中，很難獲取ρ1、ρ2和ρ3的準確值，但在生產過程相對穩定的情況下，ρ1、ρ2和ρ3的數值是相對固定的，也可以看成常數；ΔZ是由各種因素產生的變送器的零點漂移，很難準確獲得其值，但在實際生產過程相對穩定的情況下ΔZ亦為定值。從式(3)可以看出，測量液位的差壓變送器正、負壓室的壓差Δp與被測容器的液位h間呈線性關系，除了被測容器液位h是變量外，其余參數可以看成常數。由此可見，測量液位的差壓變送器正、負壓室的壓差Δp是被測容器液位h的一次函數[6,7]，即：

Δp=Kh+C

(4)

式中C——Δp與h一次函數的截距，為待求常數；

h——差壓變送器的指示液位；

K——Δp與h一次函數的斜率，為待求常數。

利用差壓變送器測量液位的目的就是要使差壓變送器的輸出值(h)與被測容器內的實際液位(h′)一致。則式(4)可以改寫成：

Δp=K′h′+C′

(5)

其中，K′和C′分別為Δp與h′一次函數的斜率和截距，是兩個待求常數。

對于智能差壓變送器可以通過375或BT200等智能通信器直接讀出與實際液位h′相對應的差壓變送器正、負壓室間的差壓Δp。h′可以通過安裝在被測容器上的就地液位計觀測，就地液位計采用的是連通器原理，一般在就地液位計保溫(冷)完好的情況下，其指示值可以看作是被測容器內的實際液位，該值既可以用絕對高度(0～H)來表示，也可用相對高度(0%～100%)來表示。

差壓變送器的準確零點是在實際工況下，實際液位最低(0%)時的差壓變送器正、負壓室間的壓差；差壓變送器的準確量程是在實際工況下，實際液位最大(100%)時差壓變送器的正、負壓室間的壓差。在實際生產過程中，不允許出現實際液位為最低或最高的工況。因此，不能直接觀測出測量液位差壓變送器的零點和量程。可利用式(5)間接地計算其準確的零點和量程，步驟如下(實際液位用相對液位%表示)：

a. 在生產過程相對穩定，被測容器就地液位計指示為h1′時，利用與差壓變送器相連接的手操器(375或BT200等)觀測出與h1′相對應的差壓變送器正、負壓室的壓差Δp1，即可得到Δp與h′的一次函數的一個坐標點(Δp1，h1′)。

b. 經過一段時間后，當被測容器就地液位計指示為h2′時，觀測出Δp與h′的一次函數的另一個坐標點(Δp2，h2′)，并且h1′≠h2′。

c. 確定被測容器液位與測量液位的差壓變送器正、負壓室間的壓差關系式。

d. 計算差壓變送器的零點和量程。

Δp0為差壓變送器的準確零點；Δp100為準確量程。將差壓變送器的零點調整為Δp0，量程調整為Δp100，則變送器的指示值與被測容器上的就地液位計的指示值在全測量范圍內就完全一致了。

5 新方法計算LT30301差壓變送器的零點和量程

通過與LT30301相連接的手操器(375)讀出差壓變送器正、負壓室間的壓差，結合表1可得表2。

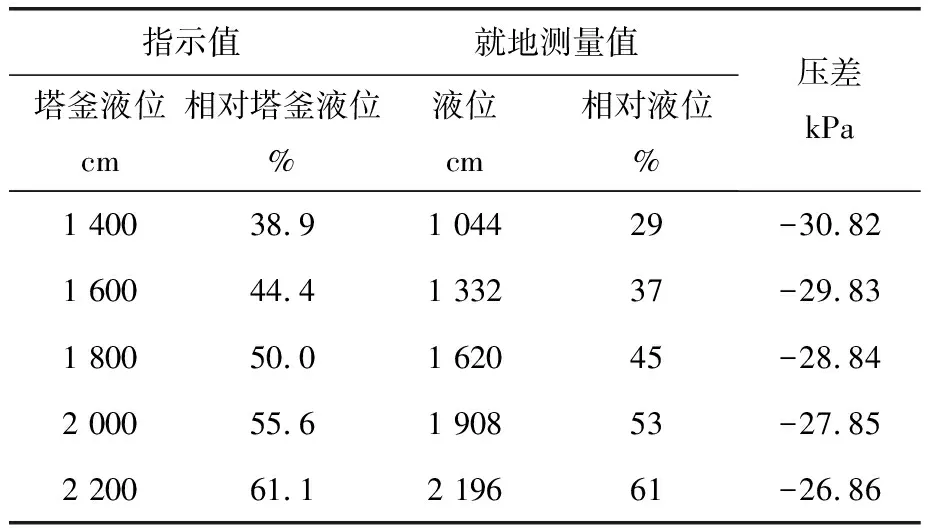
表2 含有LT30301變送器正、負壓室壓差的數據

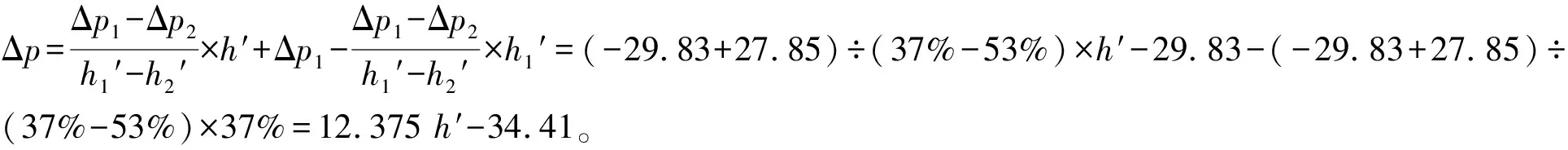
Δp=12.375h′-34.41即為T-301實際液位與變送器LT-30301正、負壓室間壓差的一次函數關系式。

當h′=0%時，Δp0=12.375h′-34.41=12.375×0%-34.41=-34.41(kPa)；當h′=100%時，Δp100=12.375h′-34.41=12.375×100%-34.41=-22.03(kPa)。Δp0為LT-30301的零點(-34.41kPa)，Δp100為LT-30301的量程(-22.03kPa)。將LT-30301的零點調整為Δp0(-34.41kPa)，LT-30301的量程調整為Δp100(-22.03kPa)，則LT-30301的指示值與被測容器上的就地液位計的指示值就完全一致了。

6 誤差分析

現在來分析利用傳統方法計算變送器的零點和量程，變送器的輸出與實際液位間的誤差。按照目前普遍采用的方法，當發現變送器的輸出與實際液位間存在誤差時，來分析只調整變送器的零點或量程，或者既調整變送器的零點又調整量程，其輸出與實際液位間的誤差。

6.1 采用傳統方法計算零點和量程時輸出與實際液位間的誤差

根據式(2)計算所得的Δp0=-37.75kPa，Δp100=-19.93kPa。當儀表指示液位為h時，根據Δp=Kh+C可得：-37.75=K×0%+C，-19.93=K×100%+C，則Δp=0.178h-37.75。

Δp=0.178h-37.75即為利用傳統計算方法計算的差壓變送器的零點和量程時所得的差壓變送器的正、負壓室壓差Δp與變送器的指示值h之間的一次函數關系式，為T-301實際液位與其變送器LT-30301正、負壓室壓差的一次函數關系式。

由Δp=12.375h′-34.41與Δp=0.178h-37.75可得如圖2所示的直角坐標關系。

圖2 直角坐標關系

圖2中，a為按關系式Δp=12.375h′-34.41得到的實際液位與其變送器LT-30301正、負壓室間的壓差所得到的直線；圖2中的b為按關系式Δp=0.178h-37.75得到的利用傳統計算方法計算的差壓變送器的零點和量程所得到的差壓變送器的正、負壓室間的壓差與變送器的指示值間的直線。

可以看出，利用傳統方法計算的差壓變送器的零點為-37.75kPa，量程為-19.93kPa，當差壓變送器的輸出為0%時實際液位為-27%；當差壓變送器的輸出為100%時實際液位為117%。當實際液位為0%時差壓變送器的輸出為18.7%；當實際液位為100%時差壓變送器的輸出為88.2%。顯然差壓變送器的輸出與實際液位之間存在很大誤差，這也進一步說明，按照傳統方法計算的儀表零點和量程無法滿足實際需要。

6.2 只調零點產生的輸出與實際液位的誤差

以儀表指示為50%為例進行分析，從表2可以看出，當差壓變送器的輸出為50%時，實際液位為45%。

按傳統方法計算的差壓變送器的零點為-37.75kPa，量程為-19.93kPa。若量程不變，只調整儀表的零點，使差壓變送器的輸出由50%變為45%，這就形成了一條新的差壓變送器正、負壓室間的壓差Δp與儀表指示h間的直線，該直線的一個坐標點為(Δp100，h100)即(-19.93，100)。當儀表指示為50%時，從表2可以看出，此時的差壓變送器的正、負壓室間的壓差為-28.84kPa。也就是說，該直線的另一點坐標為(-28.84，45)。

當儀表指示液位為h時，根據Δp=Kh+C可得-19.93=K×100%+C，-28.84=K×45%+C，則有：

Δp=0.162h-36.13

(6)

式(6)為利用按式(2)計算的差壓變送器的零點和量程，在變送器指示為50%，而實際液位(就地液位計的指示值)為45%，只調變送器的零點，使變送器的指示值由50%變為45%而得到的差壓變送器的正、負壓室間的壓差Δp與變送器的指示值h間的一次函數關系式。利用式(6)可以很容易計算并將差壓變送器的零點由-37.75kPa調至-36.13kPa，而其量程仍為-19.93kPa。

由Δp=12.375h′-34.41、Δp=0.178h-37.75和式(6)可得如圖3所示的直角坐標關系。

圖3 直角坐標關系

圖3中，直線c為按式(6)得到的直線。可以看出，當差壓變送器的輸出為0%時實際液位為-13.9%；當輸出為100%時，實際液位為117%。當實際液位為0%時，差壓變送器的輸出為10.6%；當實際液位為100%時，差壓變送器的輸出為87%。顯然差壓變送器的輸出與實際液位之間仍存在較大誤差，因此當變送器的輸出與實際液位存在誤差時只調整差壓變送器的零點是無法滿足實際需要的。

6.3 只調量程產生的輸出與實際液位的誤差

仍以儀表指示為50%為例進行分析，當差壓變送器的輸出為50%時，實際液位為45%。

傳統方法計算的差壓變送器的零點為-37.75kPa，量程為-19.93kPa。若零點不變，只調整變送器的量程，使差壓變送器的輸出值由50%變為45%，這樣就形成了一條新的差壓變送器正、負壓室間的壓差Δp與儀表指示h間的直線，該直線的一個坐標點為(Δp0，h0)(-37.75，0)。當儀表指示為50%時，根據表2，此時的正、負壓室間的壓差為-28.84kPa。也就是說，該直線的另一點坐標為(-28.84，45)。

當儀表指示液位為h時，根據Δp=Kh+C得-37.75=K×0%+C，-28.84=K×45%+C，則有：

Δp=0.198h-37.75

(7)

式(7)為利用傳統計算方法計算的差壓變送器的零點與量程，在變送器指示為50%，而實際液位(就地液位計的指示值)為45%，只調變送器的量程，使變送器的指示值由50%變為45%而得到的差壓變送器的正、負壓室間的壓差Δp與變送器的指示值h間的一次函數關系式。

由Δp=12.375h′-34.41、Δp=0.178h-37.75、式(6)和式(7)可得如圖4所示的直角坐標關系直線圖，其中的直線d為按關系式(7)得到的直線。

圖4 直角坐標關系

按式(7)計算差壓變送器的零點仍為-37.75kPa，量程由-19.93kPa變為-17.95kPa。從圖4可以看出：當差壓變送器的輸出為100%時，實際液位為133%；當輸出為0%時，實際液位為-27%。當實際液位為0%時，輸出為16.9%；當實際液位為100%時，輸出為79.4%。顯然差壓變送器的輸出與實際液位之間存在較大誤差，因此當變送器的輸出與實際液位存在誤差時只調整差壓變送器的量程也無法滿足實際需要。

6.4 既調整零點又調整量程時的誤差分析

還是以儀表指示為50%為例，當差壓變送器的輸出為50%時，實際液位為45%。如果既調整其零點又調整量程，使差壓變送器的輸出值由50%變為45%，從表2可以看出，此時差壓變送器的正、負壓室間的壓差為-28.84kPa。只要Δp0<Δp100就能滿足差壓變送器的零點和量程設置要求。眾所周知，在滿足變送器的零點和量程設置要求的情況下，通過一個坐標點(-28.84，+45.00)的直線可以有無數條，只能使這一點滿足實際要求，而使變送器的輸出與實際液位在全測量范圍內相一致的可能性很小。因此當變送器的輸出與實際液位存在誤差時既調整差壓變送器的零點又調整變送器的量程是很難滿足實際需要的。

7 利用本方法時的注意事項

在利用本方法計算變送器的零點和量程時，應注意如下事項：

a. 在讀取就地液位計和變送器的數據時，需要與生產工藝工作人員相互配合，要采取措施保證生產過程平穩，所讀取的數據一定要在生產裝置允許波動的范圍內；

b. 要確保液位差壓變送器和就地液位計的選型滿足實際生產要求且投用正常，就地液位計保溫或保冷良好，就地液位計的示值能夠真實反映被測容器的液位；

c. 要在生產過程相對平穩的情況下，讀取就地液位計的數據和變送器的數據，確保獲得的數據是真實有效的；

d. 當環境溫度或生產工藝條件發生較大變化時，需要利用本方法修正差壓變送器的零點和量程，以免差壓變送器的指示液位與被測容器上的就地液位計指示液位出現較大誤差。

8 結束語

筆者給出消除雙法蘭智能差壓變送器液位測量誤差的計算方法，不需要準確的被測容器內介質的密度、差壓變送器正、負取壓管內介質的密度和差壓變送器正、負取壓管的長度，只采用本方法計算差壓變送器的零點和量程，就可以使差壓變送器的指示液位與就地液位計的指示液位完全一致。從而間接地消除了由于各參數的密度及變送器的零點漂移等因素對計算液位差壓變送器零點和量程的影響。

本方法不但適用于差壓變送器(法蘭型與非法蘭型、智能型與非智能型)測量液位，同樣也適用于利用雙法蘭差壓變送器來測量兩種互不相溶混合液體的界位，如油水界面。經多次實踐證明，本方法完全能滿足生產實際的需要。為計算測量液位的差壓變送器以及測量兩種互不相溶混合液體界位的雙法蘭差壓變送器的零點和量程，提供了一種新的計算方法。